Conservation Theorems Section 7 9 CONSERVATION OF ENERGY

Conservation Theorems Section 7. 9 CONSERVATION OF ENERGY • Consider the general, total time derivative of the Lagrangian: L = L(qj, t) = T - U (d. L/dt) = ( L/ t) + ∑j qj ( L/ qj) + ∑j qj( L/ qj) (1) • Recall from Ch. 2: In an inertial reference frame, time is homogeneous (the same for all space!) In a closed system the Lagrangian L = T - U cannot depend EXPLICITLY on the time! ( L/ t) = 0 (2) • Also, Lagrange’s Equations are: ( L/ qj) = (d/dt)[( L/ qj)] (3)

Conservation of Energy • Use (2) & (3) in (1): (d. L/dt) = ∑j qj(d/dt)[( L/ qj)] + ∑j qj( L/ qj) (4) • The right side of (4) is (from the chain rule!): = ∑j(d/dt)[qj ( L/ qj)] = (d/dt)[∑j qj ( L/ qj)] (4) becomes: (d/dt)[L - ∑j qj ( L/ qj)] = 0 (5) Or: [L - ∑ j qj ( L/ qj)] = constant in time • Define H ∑j qj ( L/ qj) - L (6) (5) (d. H/dt) = 0 Or: H = constant in time

Define H ∑j qj( L/ qj) - L (6) (d. H/dt) = 0, H = constant in time • H The Hamiltonian of the system. Defined formally like this. See the next section for more details. • Of course L = T – U. In the usual case, the PE is independent of generalized the velocities U = U(qj) ( L/ qj) = ( [T-U]/ qj) = ( T/ qj) • Put this into (6): H = ∑j qj( T/ qj) - (T - U) • In the previous section, we proved: ∑j qj( T/ qj) 2 T H = 2 T - (T - U) or H = T + U = E = TOTAL MECHANICAL ENERGY!!

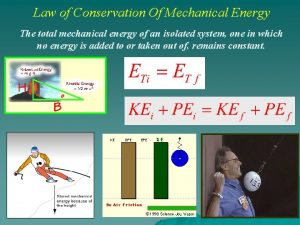
• Summary: For a closed system in which KE is a homogeneous, quadratic function of the generalized velocities: 1. The Lagrangian L = T - U = constant in time. 2. The Hamiltonian H is defined: H ∑j qj ( L/ qj) - L 3. H = T + U = E = Total Mechanical Energy 4. H = E = constant in time (“A constant of the motion”) Conservation of Total Mechanical Energy!

• The Hamiltonian H (its main use discussed soon!): H ∑j qj ( L/ qj) – L • Example: Particle, mass m in a plane, subject to gravitational force. Use plane polar coordinates. L = T – U = (½)m(r 2 + r 2θ 2) – mgr cosθ H = r( L/ r) + θ( L/ θ) – L H = m(r 2 + r 2θ 2) - L H = (½)m(r 2 + r 2θ 2) + mgr cosθ = T + U

Discussion • The definition of the Hamiltonian H ∑j qj ( L/ qj) – L is general! • The relation H = T + U = E is valid ONLY under the conditions of the derivation (!): – The eqtns of transformation connecting rectangular & generalized coords must be independent of time T is a homogeneous, quadratic function of qj. – Then potential energy U must be independent of the generalized velocities qj.

• Two questions pertaining to any system: 1. Does the Hamiltonian H = E for the system? 2. Is energy E conserved for the system? • These are two DIFFERENT aspects of the problem! – Could have H E, but also have energy E conserved. – For example: In a conservative system, using generalized coordinates which are in motion with respect to fixed rectangular axes: the Transformation eqtns will contain the time T will NOT be a homogeneous, quadratic function of the generalized velocities! H E, However, because the system is conservative the total energy E is conserved! (This is a physical fact about the system, independent of coordinate choices).

Momentum Conservation • Recall from Ch. 2: In an inertial reference frame, space is homogeneous: In a closed system the Lagrangian L = T - U cannot be affected by a uniform translation of the system! i. e. , Changing every coordinate vector rα by an infinitesimal translation: rα + δr leaves L unchanged. • The displacement δr is a displacement in the virtual (variational) sense (as opposed to a real, physical displacement dr).

• For simplicity, consider a closed system (so that L has no explicit time dependence: ( L/ t) = 0) with a single particle & use rectangular coordinates: L = L(xi, xi) • Consider the change in L caused by an infinitesimal displacement δr ∑i ei δxi : δL= ∑i( L/ xi)δxi+ ∑i( L/ xi) δxi (1) This leaves L unchanged δL = 0 (2) • Consider varied displacements only the δxi are time independent! δxi = δ(dxi/dt) = (d[δxi]/dt) 0 (3)

• Combine (1), (2), (3): δL= ∑i ( L/ xi)δxi = 0 (4) • Each δxi is an independent displacement (4) is valid only if ( L/ xi) = 0 (i =1, 2, 3) (5) • Lagrange’s Equations are: ( L/ xi) = (d/dt)[( L/ xi)] (6) • (5) & (6) together (d/dt)[( L/ xi)] = 0 Or: ( L/ xi) = constant in time (7)

( L/ xi) = constant in time (A) • Physically, what is ( L/ xi)? L = T - U, T = T(xi), U = U(xi), ( L/ xi) = ( [T - U]/ xi) = ( T/ xi) • Note: ( T/ xi) = ( [(½)m∑j (xj)2]/ xi) = mxi = pi ( L/ xi) = pi = LINEAR MOMENTUM! Summary: (A) The homogeneity of space The linear momentum p of a closed system (no external forces) is constant in time! (Momentum is conserved!) Or, if the Lagrangian of a system is invariant with respect to uniform translation in a certain direction, the component of linear momentum of the system in that direction is conserved (constant in time).

Angular Momentum Conservation • Recall from Ch. 2: In an inertial reference frame, space is isotropic (the same in every direction!) In a closed system the Lagrangian L = T - U cannot be affected by a uniform, infinitesimal rotation of the system! Rotation through an infinitesimal angle δθ is shown. Angle δθ has vector direction δθ to plane, as shown.

• For simplicity, again consider a closed system (so that L has no explicit time dependence: ( L/ t) = 0) with a single particle & use rectangular coordinates: L = L(xi, xi) • Consider the change in L caused by a rotation through an infinitesimal angle δθ as in the figure. Each radius vector (vector arrows left off!) r changes to r + δr where (from Ch. 1) δr δθ r (1) • Velocity vectors also change on rotation: Velocities r change to r + δr, where (from Ch. 1) δr δθ r (2) • The change in the Lagrangian due to δθ is: δL= ∑i( L/ xi)δxi+ ∑i( L/ xi) δxi (3)

• From previous discussion: ( L/ xi) = pi (linear momentum) • Lagrange’s Equations are: ( L/ xi) = (d/dt)[( L/ xi)] ( L/ xi) = (dpi/dt) = pi • (3) on the previous page becomes: δL= ∑ i pi δxi+ ∑ i pi δxi = 0 • Or, in vector notation (arrows left off!): δL = p δr + p δr = 0 (4) • Using (1) & (2) in (4): p (δθ r) + p (δθ r) = 0 (5) • Using vector identity (triple scalar product properties), (5) is: δθ [(r p) + (r p)] = 0 Or: δθ [d(r p)/dt] = 0 (6) • δθ is arbitrary: [d(r p)/dt] = 0 Or: (r p) = constant in time!

• For arbitrary δθ (r p) = constant in time! • Using the definition of angular momentum: L (r p) L = constant in time Distinguish angular momentum L from the Lagrangian L! • We have shown that, for a closed system, the isotropy of space the angular momentum is a constant in time: Angular Momentum is conserved! • Corollary: If system is in external force field with an axis of symmetry, the Lagrangian is invariant with respect to rotations about the symmetry axis. The angular momentum about that symmetry axis is conserved!

Symmetry Properties; Conservation Laws Repeat of a Discussion from Ch. 2! • In general, in physical systems: A Symmetry Property of the System Conservation of Some Physical Quantity Also: The conservation of Some Physical Quantity A Symmetry Property of the System • This isn’t just valid in classical mechanics! Also in quantum mechanics! This forms the foundation of modern theories (Quantum Field Theory, Elementary Particles, …)

Summary: Conservation Laws • In a closed system, in an inertial reference frame, we’ve shown that symmetry properties & conservation laws are directly related. This is often called Noether’s Theorem (after Emmy Noether, see footnote, p. 264).

• For a closed system (no external forces) in an inertial reference frame, there are 7 “Constants of the Motion” “Integrals of the Motion” Quantities which are Conserved (constant in time): The Total Mechanical Energy (E) The 3 vector components of the Linear Momentum (p) The 3 vector components of the Angular Momentum (L)