Conjugate Gradient Methods for Largescale Unconstrained Optimization Dr

Conjugate Gradient Methods for Large-scale Unconstrained Optimization Dr. Neculai Andrei Research Institute for Informatics Bucharest and Academy of Romanian Scientists Ovidius University, Constantza - Romania, March 27, 2008

Contents § § § Problem definition Unconstrained optimization methods Conjugate gradient methods - Classical conjugate gradient algorithms - Hybrid conjugate gradient algorithms - Scaled conjugate gradient algorithms - Modified conjugate gradient algorithms - Parametric conjugate gradient algorithms § Applications

Problem definition - continuously differentiable - gradient is available - n is large - Hessian is unavailable Necessary optimality conditions: Sufficient optimality conditions:

Unconstrained optimization methods Step length Search direction 1) Line search 2) Trust-Region algorithms Quadratic approximation Influences

Step length computation: 1) Armijo rule: 2) Goldstein rule:

3) Wolfe conditions: Implementations: Shanno (1978) Moré - Thuente (1992 -1994)

Proposition Assume that is a descent direction and satisfies the Lipschitz condition for all where on the line segment connecting and is a positive constant. If the line search satisfies the Goldstein conditions then If the line search satisfies the Wolfe conditions, then

Remarks: 1) The Newton method, the quasi-Newton or the limited memory quasi-Newton methods has the ability to accept unity step lengths along the iterations. 2) In conjugate gradient methods the step lengths may differ from 1 in a very unpredictable manner. They can be larger or smaller than 1 depending on how the problem is scaled*. *N. Andrei, (2007) Acceleration of conjugate gradient algorithms for unconstrained optimization. (submitted JOTA)

Methods for Unconstrained Optimization 1) Steepest descent (Cauchy, 1847) 2) Newton 3) Quasi-Newton (Broyden, 1965; and many others)

4) Conjugate Gradient Methods (1952) is known as the conjugate gradient parameter 5) Truncated Newton method (Dembo, et al, 1982) 6) Trust Region methods

7) Conic model method (Davidon, 1980) 8) Metode tensoriale (Schnabel & Frank, 1984)

9) Methods based on systems of Differential Equations Gradient flow Method (Courant, 1942) 10) Direct searching methods Hooke-Jevees (form searching) (1961) Powell (conjugate directions) (1964) Rosenbrock (coordinate system rotation)(1960) Nelder-Mead (rolling the simplex) (1965) Powell –UOBYQA (quadratic approximation) (1994 -2000) N. Andrei, Critica Retiunii Algoritmilor de Optimizare fara Restrictii Editura Academiei Romane, 2008.

Conjugate Gradient Methods Magnus Hestenes (1906 -1991) Eduard Stiefel (1909 -1978)

The prototype of Conjugate Gradient Algorithm Step 1. Select the initial starting point: Step 2. Test a criterion for stopping the iterations. Step 3. Determine the steplength by Wolfe conditions. Step 4. Update the variables: ► Step 5. Compute: Step 6. Compute the search direction: Step 7. Restart. If: then set Step 8. Compute the initial guess: and continue with step 2. set

Convergence Analysis Theorem. Suppose that: 1) the level set 2) the function is bounded, is continuously differentiable, 3) the gradient is Lipschitz continuous, i. e. Consider any conjugate gradient method where: is a descent direction, 1) 2) is obtained by the strong Wolfe line search. If then

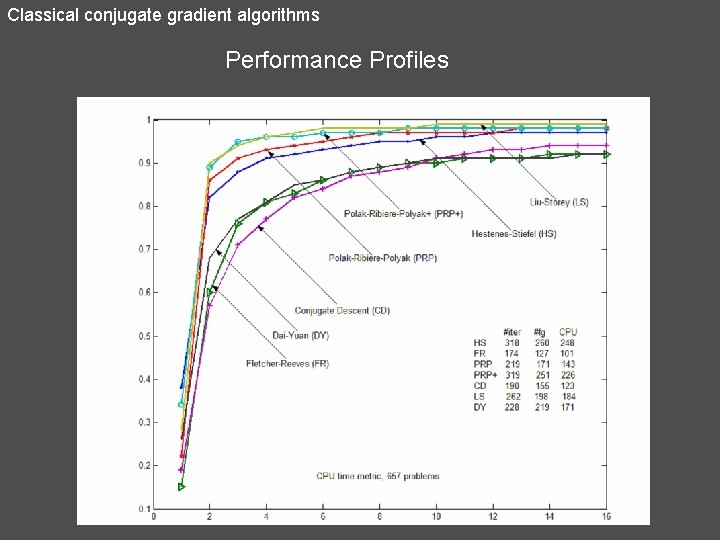
Classical conjugate gradient algorithms 1. Hestenes - Stiefel (HS) 2. Polak – Ribière - Polyak (PRP) 3. Liu - Storey (LS) 4. Fletcher - Reeves (FR) 5. Conjugate Descent – Fletcher (CD) 6. Dai – Yuan (DY)

Classical conjugate gradient algorithms Performance Profiles

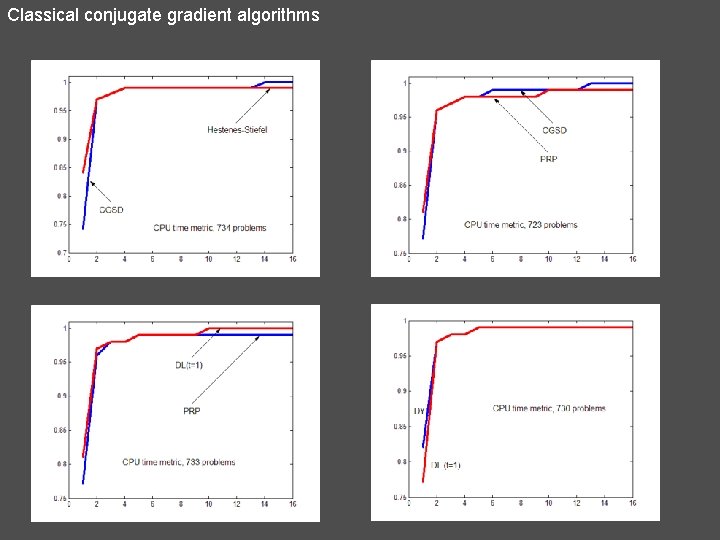
Classical conjugate gradient algorithms 7. Dai – Liao (DL) 8. Dai – Liao plus (DL+) 9. Andrei - Sufficient Descent Condition (CGSD)* * N. Andrei, A Dai-Yuan conjugate gradient algorithm with sufficient descent and conjugacy conditions for unconstrained optimization. Applied Mathematics Letters, vol. 21, 2008, pp. 165 -171.

Classical conjugate gradient algorithms

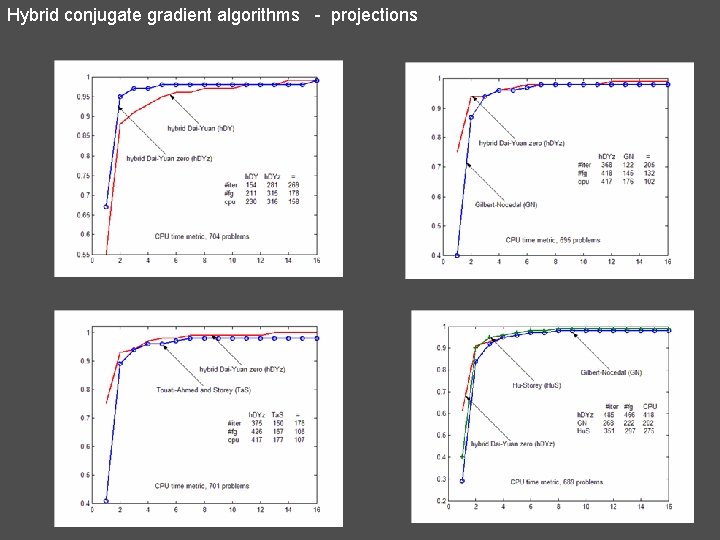
Hybrid conjugate gradient algorithms - projections 10. Hybrid Dai - Yuan (h. DY) 11. Hybrid Dai – Yuan zero (h. DYz) 12. Gilbert – Nocedal (GN)

Hybrid conjugate gradient algorithms - projections 13. Hu – Storey (Hu. S) 14. Touati-Ahmed and Storey (Ta. S) 15. Hybrid LS – CD (LS-CD)

Hybrid conjugate gradient algorithms - projections

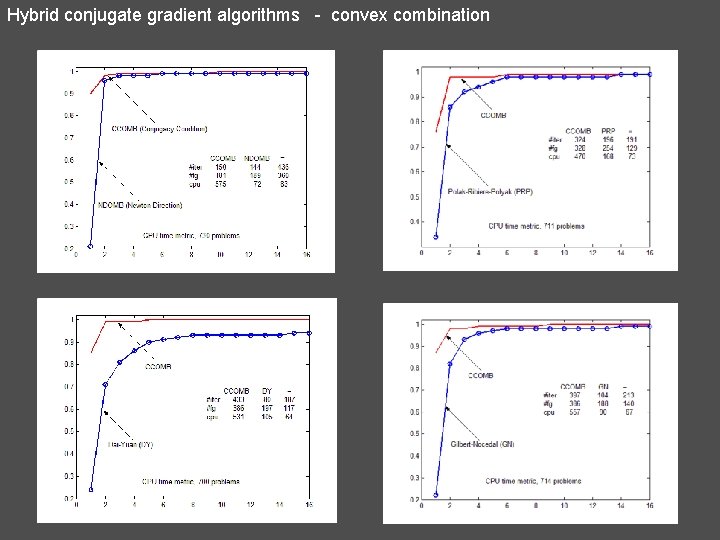
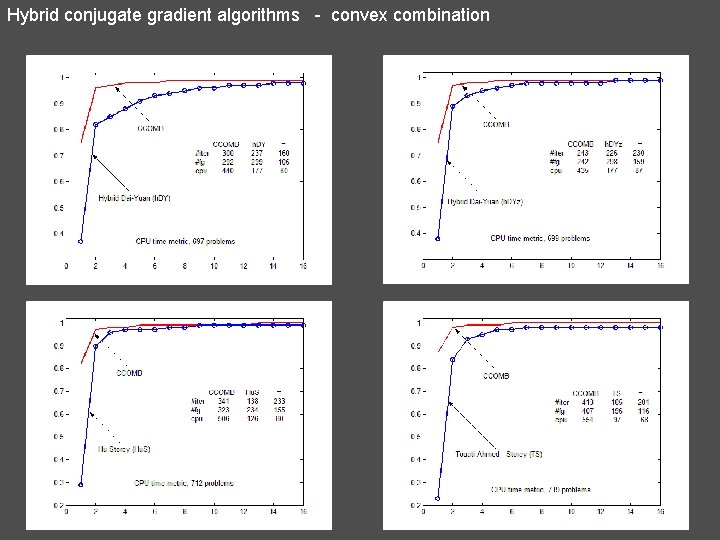
Hybrid conjugate gradient algorithms - convex combination 16. Convex combination of PRP and DY from conjugacy condition (CCOMB - Andrei) If then N. Andrei, New hybrid conjugate gradient algorithms for unconstrained optimization. Encyclopedia of Optimization, 2 nd Edition, Springer, August 2008, Entry 761.

Hybrid conjugate gradient algorithms - convex combination 17. Convex combination of PRP and DY from Newton direction (NDOMB - Andrei) If then N. Andrei, New hybrid conjugate gradient algorithms as a convex combination of PRP and DY for unconstrained optimization. ICI Technical Report, October 1, 2007. (submitted AML)

Hybrid conjugate gradient algorithms - convex combination

Hybrid conjugate gradient algorithms - convex combination

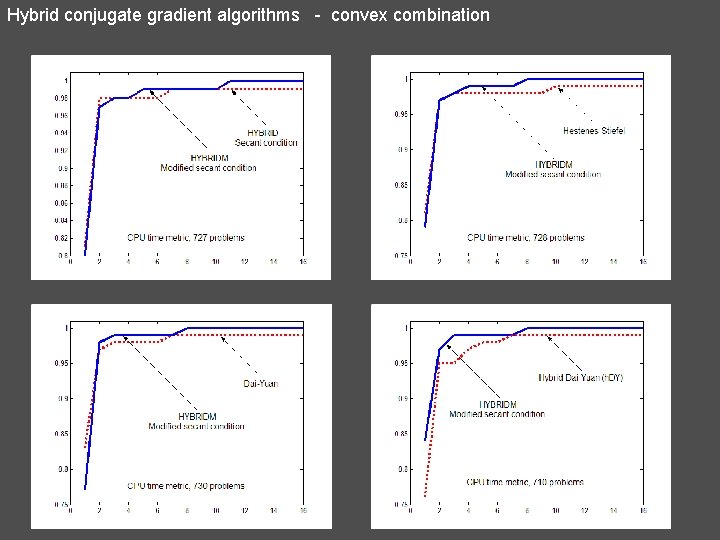
Hybrid conjugate gradient algorithms - convex combination 18. Convex combination of HS and DY from Newton direction (HYBRID - Andrei) (Secant condition) If then N. Andrei, A hybrid conjugate gradient algorithm for unconstrained optimization as a convex combination of Hestenes-Stiefel and Dai-Yuan. Studies in Informatics and Control, vol. 17, No. 1, March 2008, pp. 55 -70.

Hybrid conjugate gradient algorithms - convex combination 19. Convex combination of HS and DY from Newton direction with modified secant condition (HYBRIDM - Andrei) If then N. Andrei, A hybrid conjugate gradient algorithm with modified secant condition for unconstrained optimization. ICI Technical Report, February 6, 2008 (submitted to Numerical Algorithms)

Hybrid conjugate gradient algorithms - convex combination

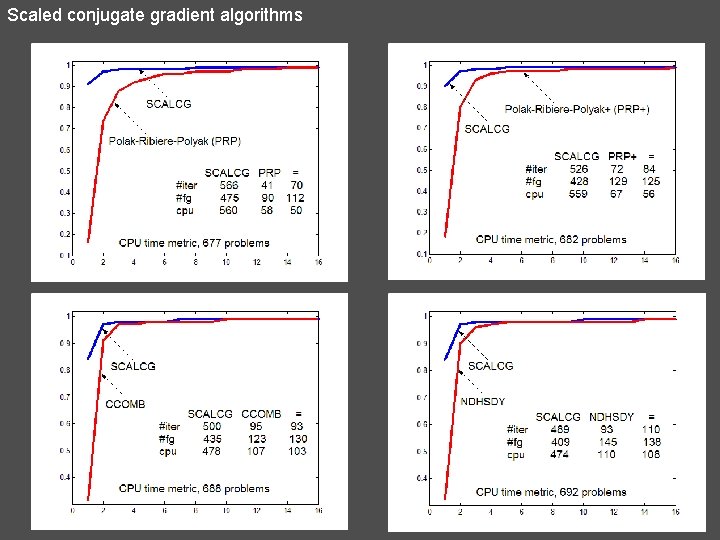
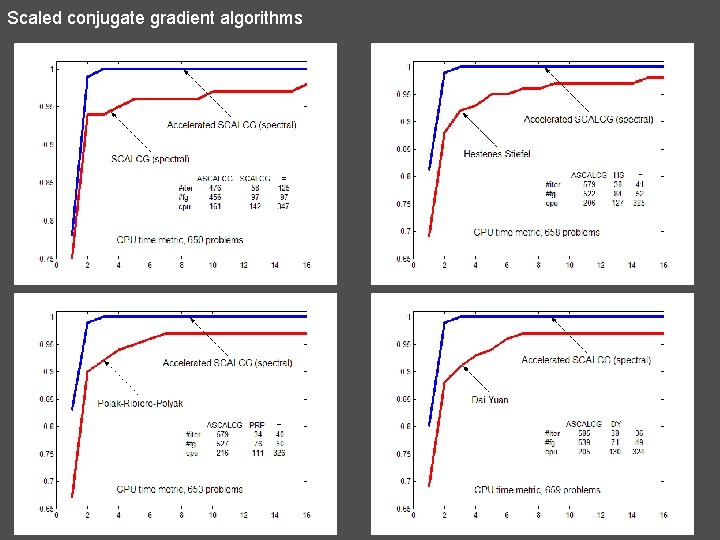
Scaled conjugate gradient algorithms N. Andrei, Scaled memoryless BFGS preconditioned conjugate gradient algorithm for unconstrained optimization. Optimization Methods and Software, 22 (2007), pp. 561 -571.

Scaled conjugate gradient algorithms A) Secant Condition B) Modified secant Condition N. Andrei, Accelerated conjugate gradient algorithm with modified secant condition for unconstrained optimization. ICI Technical Report, March 3, 2008. (Submitted, JOTA, 2007)

Scaled conjugate gradient algorithms C) Hessian / vector approximation by finite difference N. Andrei, Accelerated conjugate gradient algorithm with finite difference Hessian / vector product approximation for unconstrained optimization. ICI Technical Report, March 4, 2008 (submitted Math. Programm. )

Scaled conjugate gradient algorithms 20. Birgin – Martínez (BM) 21. Birgin – Martínez plus (BM+) 22. Scaled Polak-Ribière-Polyak (s. PRP)

Scaled conjugate gradient algorithms 23. Scaled Fletcher – Reeves (s. FR) 24. Scaled Hestenes – Stiefel (s. HS)

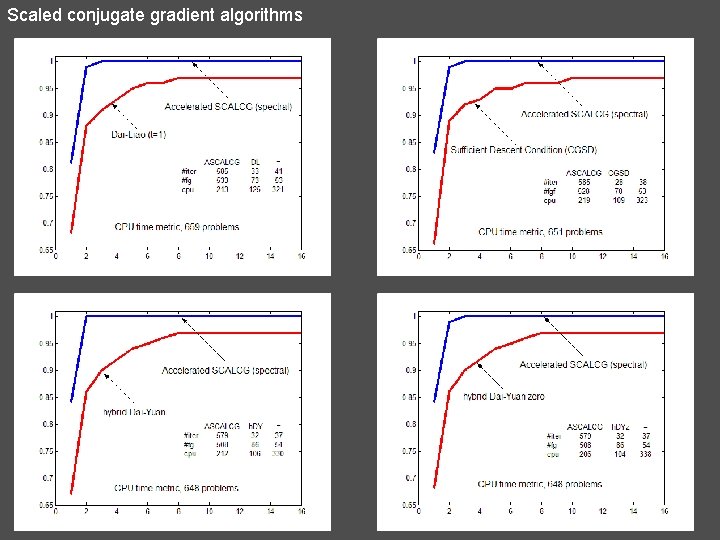
Scaled conjugate gradient algorithms 25. SCALCG (secant condition) N. Andrei, Scaled conjugate gradient algorithms for unconstrained optimization. Computational Optimization and Applications, vol. 38, no. 3, (2007), pp. 401 -416.

Scaled conjugate gradient algorithms Theorem Suppose that then the direction satisfies the Wolfe conditions is a descent direction. N. Andrei, A scaled BFGS preconditioned conjugate gradient algorithm for unconstrained optimization. Applied Mathematics Letters, 20 (2007), pp. 645 -650.

Scaled conjugate gradient algorithms The Powell restarting procedure : The direction is computed using a double update scheme: for ANDREI, N. , A scaled nonlinear conjugate gradient algorithm for unconstrained optimization. Optimization. A journal of mathematical programming and operations research, DOI, accepted.

Scaled conjugate gradient algorithms N. Andrei, Scaled memoryless BFGS preconditioned conjugate gradient algorithm for unconstrained optimization. Optimization Methods and Software, 22 (2007), pp. 561571.

Scaled conjugate gradient algorithms Lemma: If Lipschitz continuous, then Theorem: For strongly convex functions, with Wolfe line search

Scaled conjugate gradient algorithms

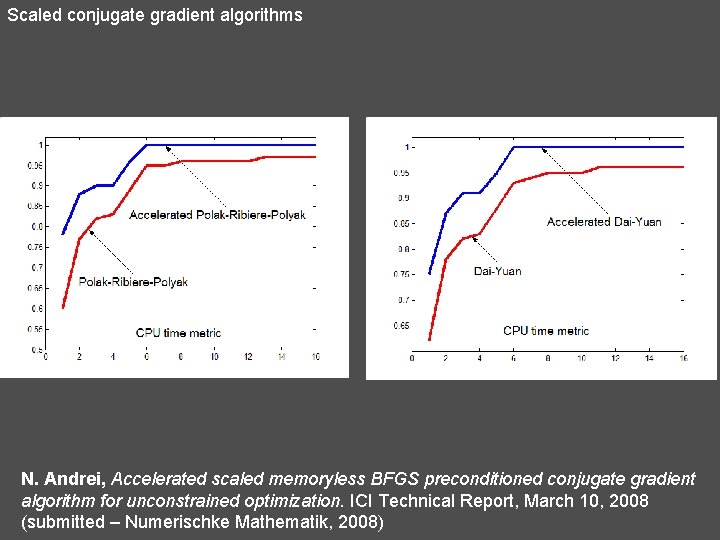
Scaled conjugate gradient algorithms 26. ASCALCG (secant condition) In conjugate gradient methods the step lengths may differ from 1 in a very unpredictable manner. They can be larger or smaller than 1 depending on how the problem is scaled. General Theory of Acceleration N. Andrei, (2007) Acceleration of conjugate gradient algorithms for unconstrained optimization. ICI Technical Report, October 24, 2007. (submitted JOTA, 2007)

Scaled conjugate gradient algorithms

Scaled conjugate gradient algorithms

Scaled conjugate gradient algorithms If is a descent direction, then

Scaled conjugate gradient algorithms computation:

Proposition. Suppose that is a uniformly convex function on the level set and the sufficient descent condition and satisfies where Then the sequence generated by ACG converges linearly to solution to the optimization problem.

Scaled conjugate gradient algorithms N. Andrei, Accelerated scaled memoryless BFGS preconditioned conjugate gradient algorithm for unconstrained optimization. ICI Technical Report, March 10, 2008 (submitted – Numerischke Mathematik, 2008)

Scaled conjugate gradient algorithms

Scaled conjugate gradient algorithms

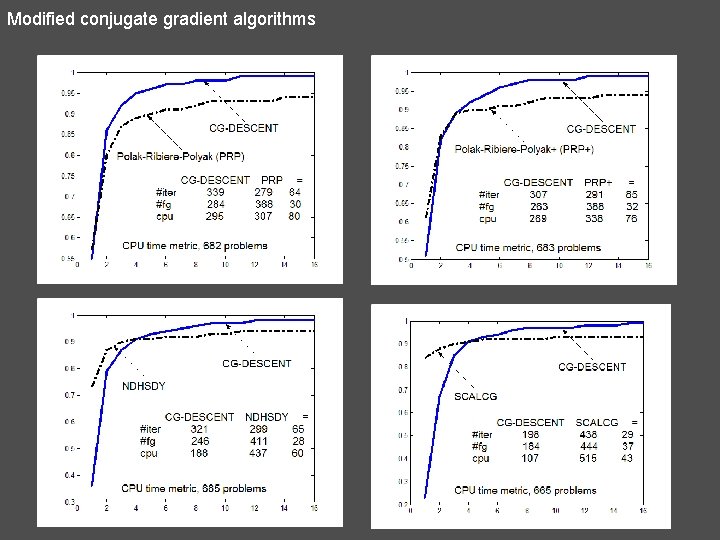
Modified conjugate gradient algorithms 27. Andrei – Sufficient Descent Condition from PRP (A-prp) 28. Andrei – Sufficient Descent Condition from DY (ACGA) 29. Andrei – Sufficient Descent Condition from DY zero (ACGA+)

Modified conjugate gradient algorithms 30) CG_DESCENT (Hager-Zhang, 2005, 2006)

Modified conjugate gradient algorithms

Modified conjugate gradient algorithms

Modified conjugate gradient algorithms

Modified conjugate gradient algorithms

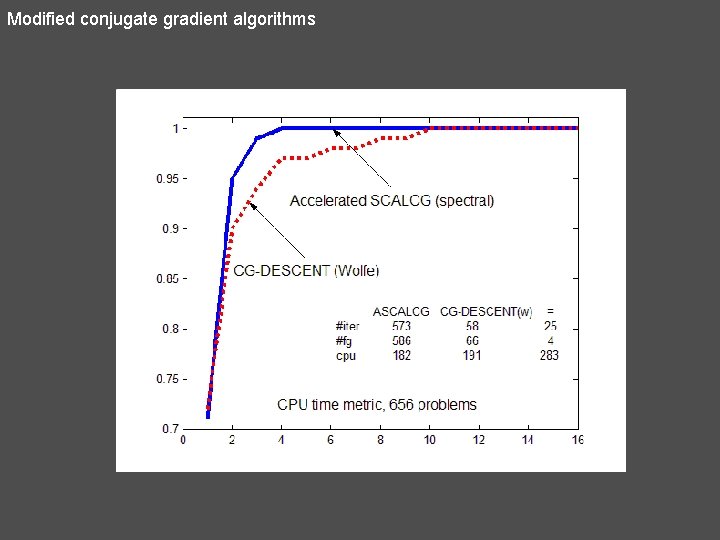
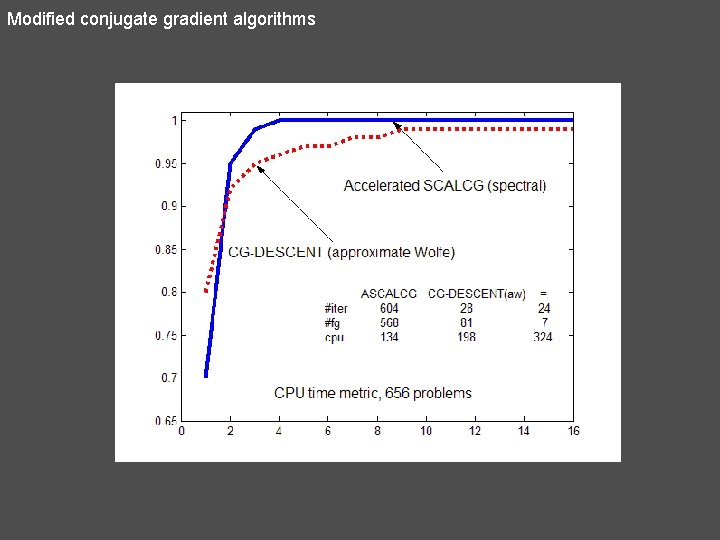
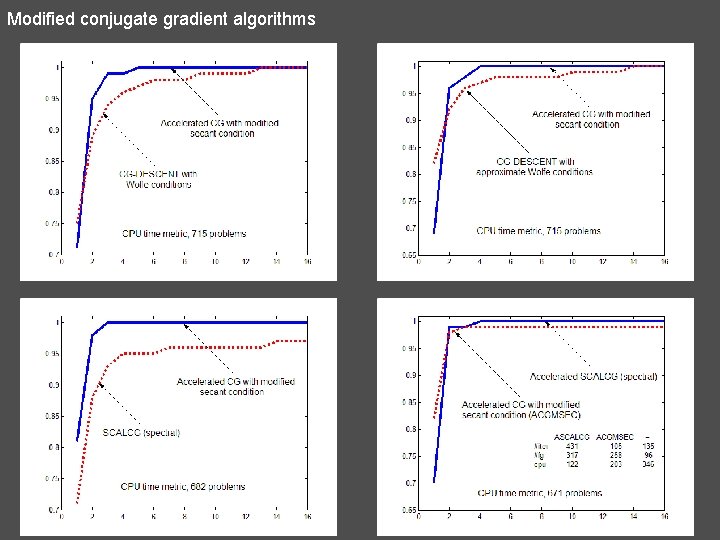
Modified conjugate gradient algorithms (Slide 30) 31) ACGMSEC For Theorem we get exactly the Perry method. If then N. Andrei, Accelerated conjugate gradient algorithm with modified secant condition for unconstrained optimization. ICI Technical Report, March 3, 2008. (Submitted: Applied Mathematics and Optimization, 2008)

Modified conjugate gradient algorithms

Modified conjugate gradient algorithms

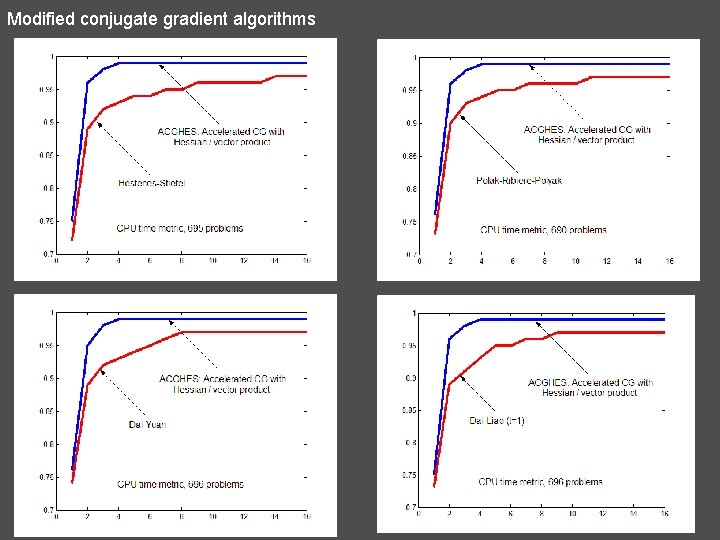
Modified conjugate gradient algorithms 32) ACGHES N. Andrei, Accelerated conjugate gradient algorithm with finite difference Hessian / vector product approximation for unconstrained optimization. ICI Technical Report, March 4, 2008 (submitted Math. Programm. )

Modified conjugate gradient algorithms

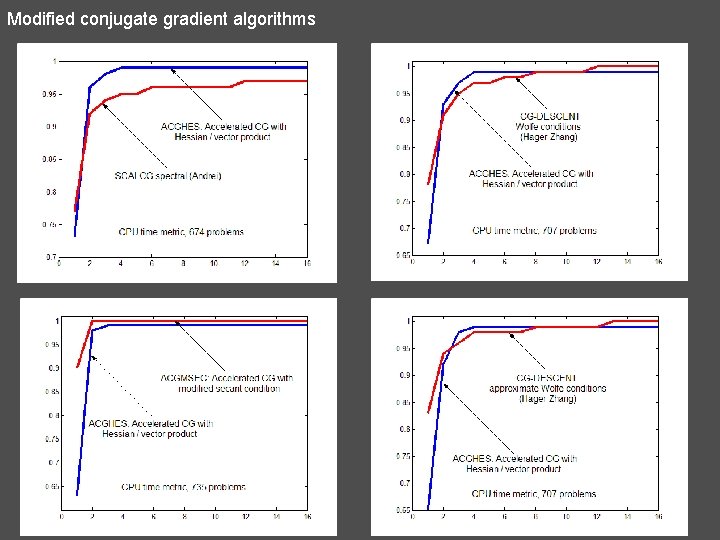
Modified conjugate gradient algorithms

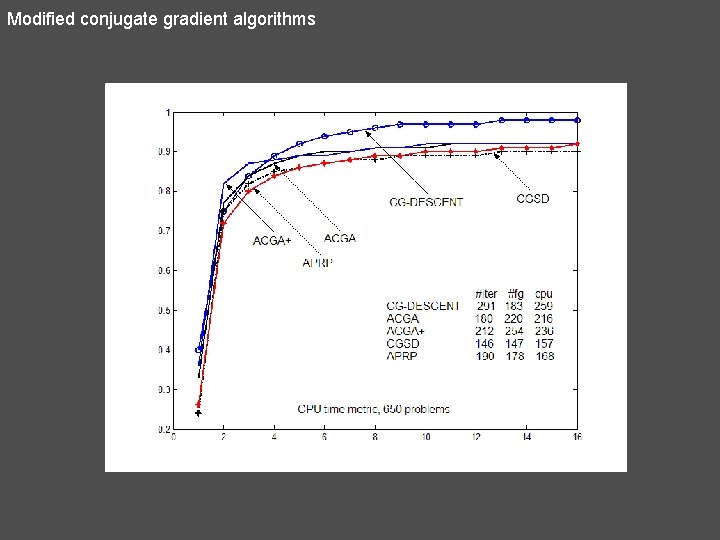
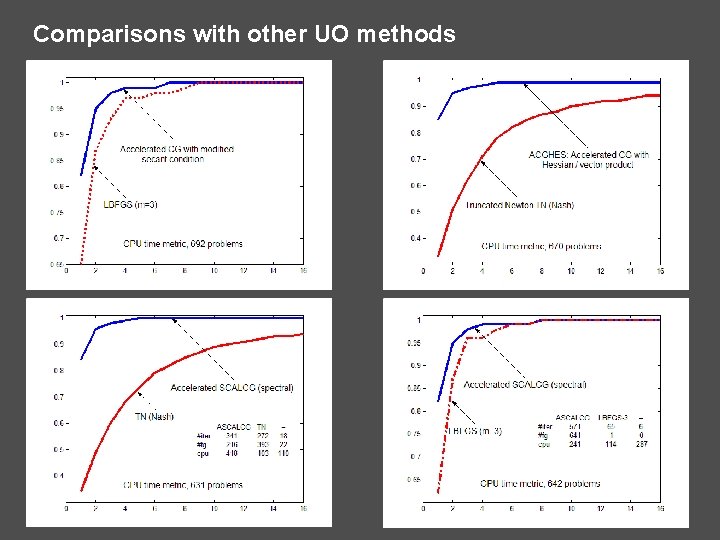
Comparisons with other UO methods

Parametric conjugate gradient algorithms 33) Yabe-Takano 34) Yabe-Takano +

Parametric conjugate gradient algorithms 35) Parametric CG suggested by Dai-Yuan 36) Parametric CG suggested by Nazareth

Parametric conjugate gradient algorithms 37) Parametric CG suggested by Dai-Yuan

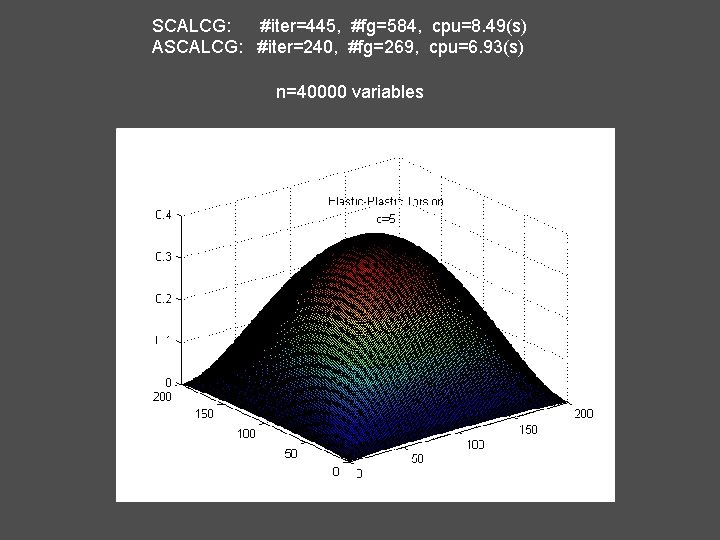
Applications A 1) Elastic-Plastic Torsion (c=5) (nx=200, ny=200) MINPACK 2 Collection

SCALCG: #iter=445, #fg=584, cpu=8. 49(s) ASCALCG: #iter=240, #fg=269, cpu=6. 93(s) n=40000 variables

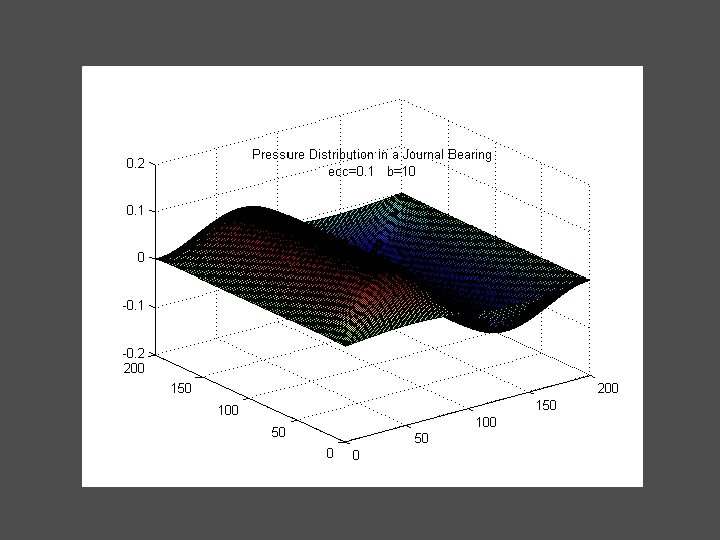
A 2) Pressure Distribution in a Journal Bearing (ecc=0. 1 b=10) (nx=200, ny=200)

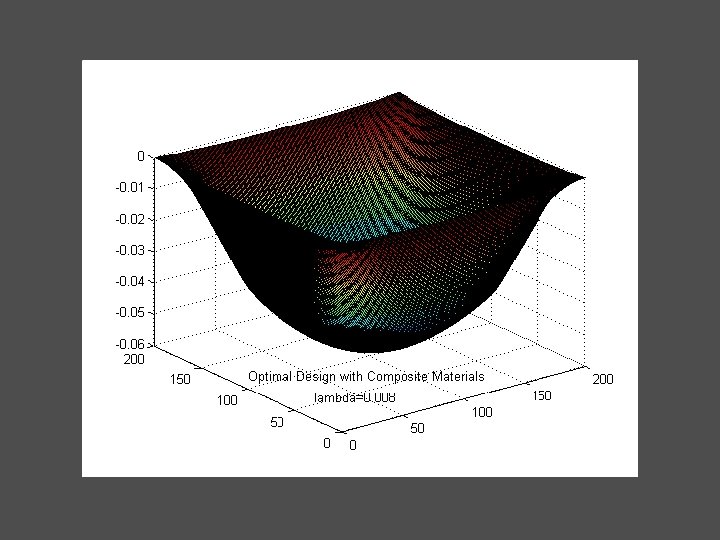
A 3) Optimal Design with Composite Materials

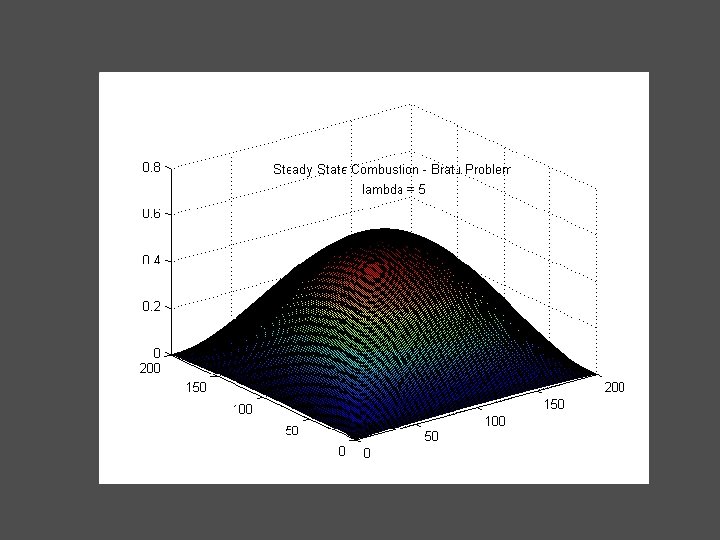
A 4) Steady State Combustion - Bratu Problem

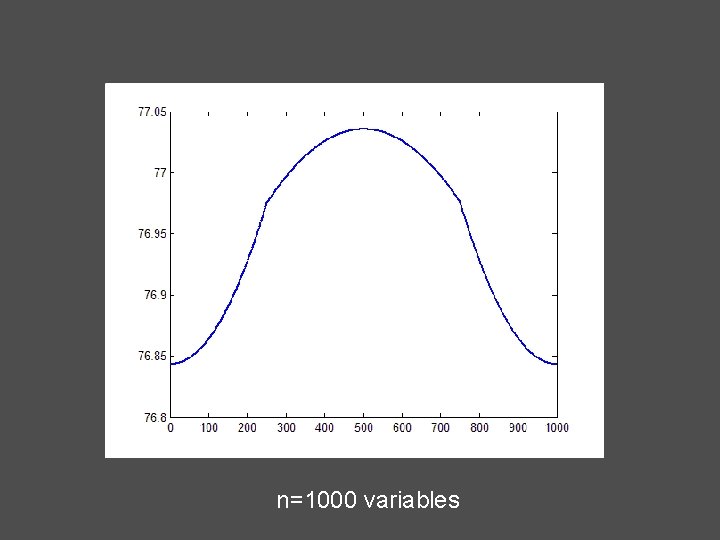
A 5) Ginzburg-Landau (1 -dimensional) Free Gibbs energy:

n=1000 variables

Thank you !