Conic Sections The Parabola Introduction Consider a cone

Conic Sections The Parabola

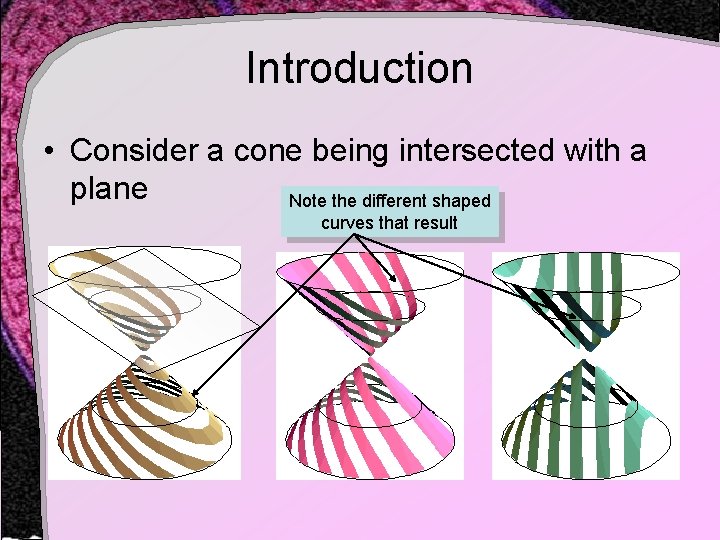
Introduction • Consider a cone being intersected with a plane Note the different shaped curves that result

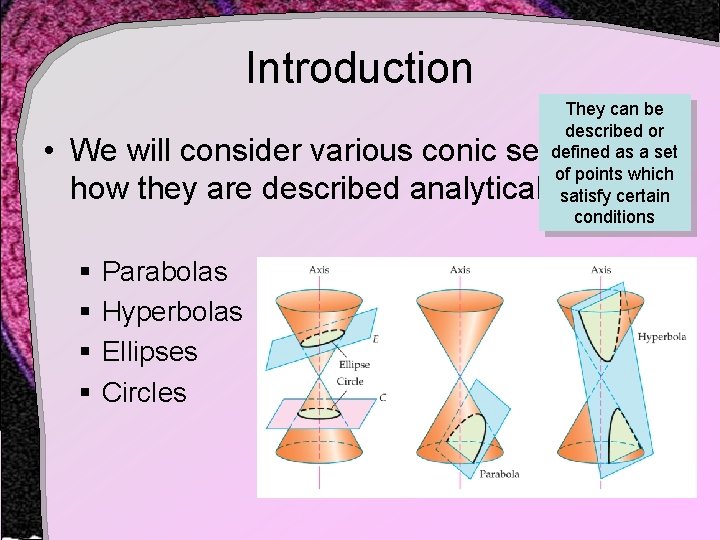
Introduction They can be described or defined as a set of points which satisfy certain conditions • We will consider various conic sections and how they are described analytically § Parabolas § Hyperbolas § Ellipses § Circles

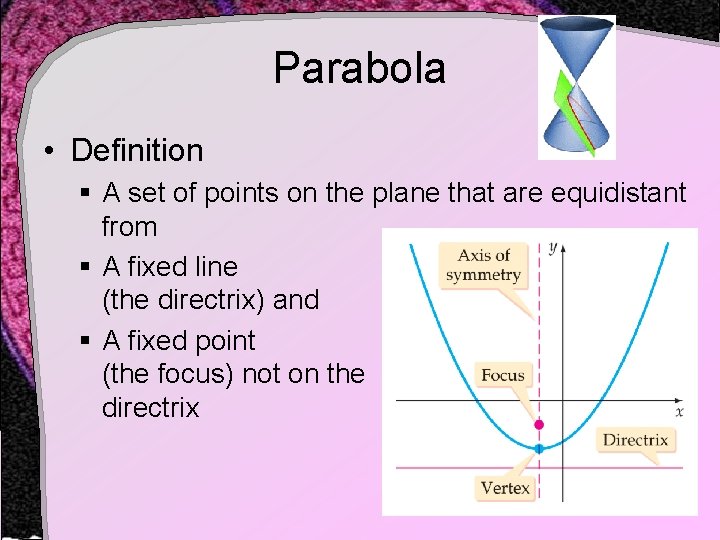
Parabola • Definition § A set of points on the plane that are equidistant from § A fixed line (the directrix) and § A fixed point (the focus) not on the directrix

Parabola • Note the line through the focus, perpendicular to the directrix § Axis of symmetry • Note the point midway between the directrix and the focus § Vertex View Geogebra Demonstration

Equation of Parabola • Let the vertex be at (0, 0) § Axis of symmetry be y-axis § Directrix be the line y = -p (where p > 0) § Focus is then at (0, p) • For any point (x, y) on the parabola Distance = y + p

Equation of Parabola • Setting the two distances equal to each other . . . simplifying. . . • What happens if p < 0? • What happens if we have

Working with the Formula • Given the equation of a parabola § y = ½ x 2 • Determine § The directrix § The focus • Given the focus at (-3, 0) and the fact that the vertex is at the origin • Determine the equation

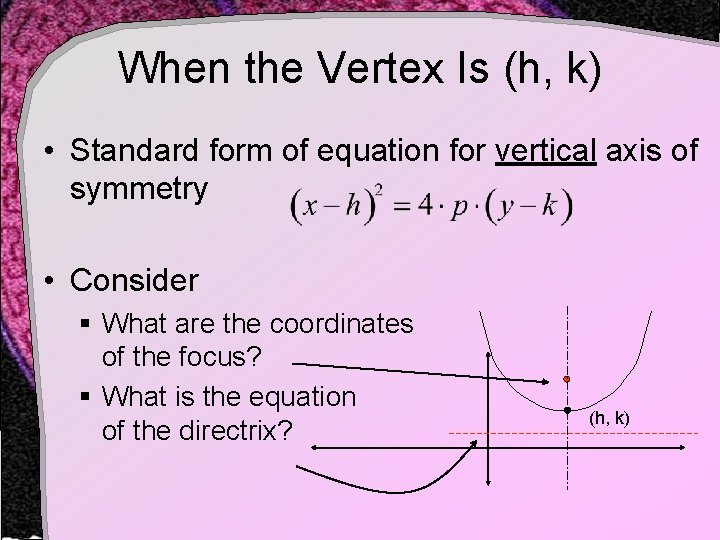
When the Vertex Is (h, k) • Standard form of equation for vertical axis of symmetry • Consider § What are the coordinates of the focus? § What is the equation of the directrix? (h, k)

When the Vertex Is (h, k) • Standard form of equation for horizontal axis of symmetry • Consider § What are the coordinates of the focus? § What is the equation of the directrix? (h, k)

Try It Out • Given the equations below, § What is the focus? § What is the directrix?

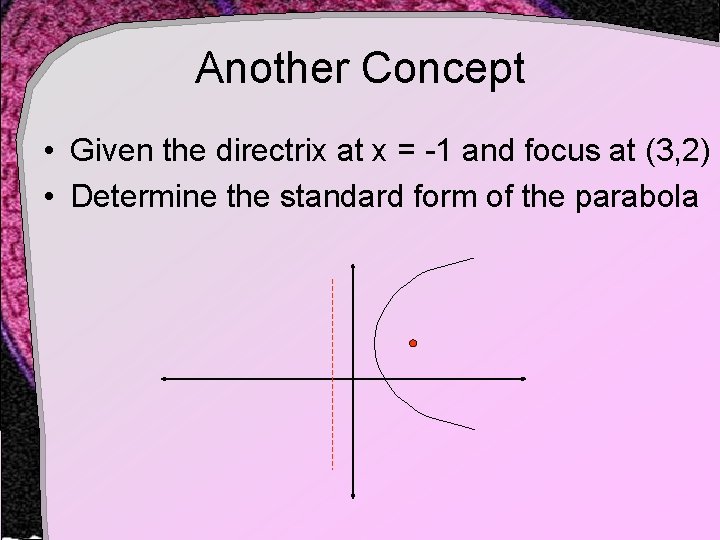
Another Concept • Given the directrix at x = -1 and focus at (3, 2) • Determine the standard form of the parabola

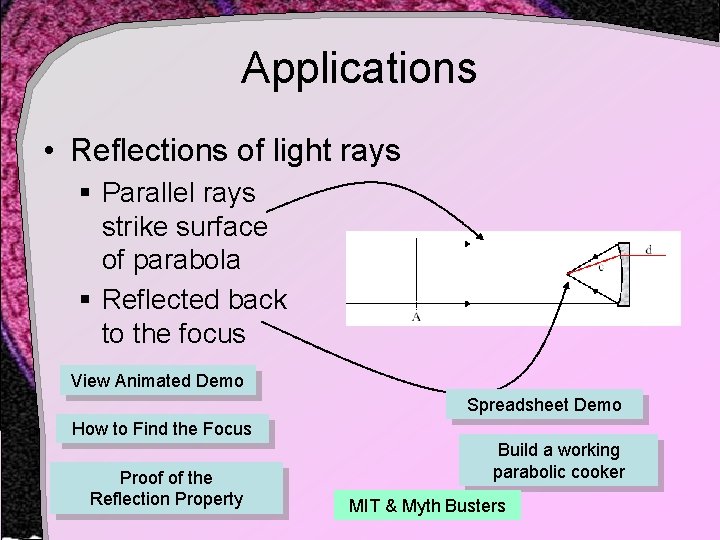
Applications • Reflections of light rays § Parallel rays strike surface of parabola § Reflected back to the focus View Animated Demo Spreadsheet Demo How to Find the Focus Proof of the Reflection Property Build a working parabolic cooker MIT & Myth Busters

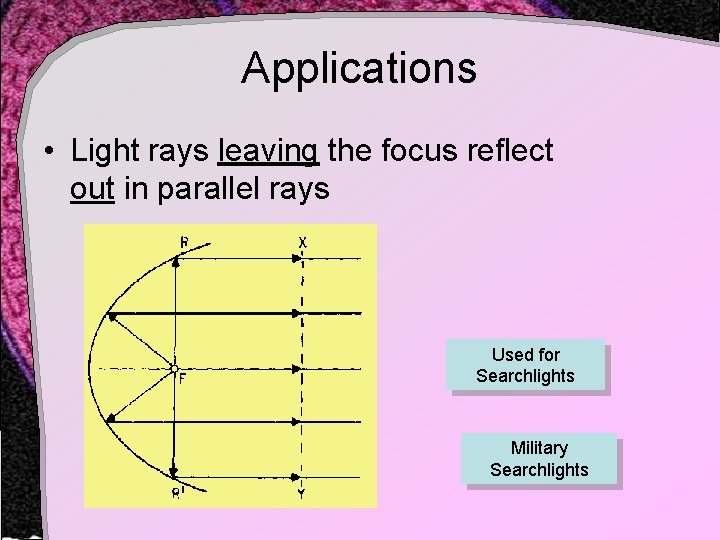
Applications • Light rays leaving the focus reflect out in parallel rays Used for Searchlights Military Searchlights

Assignment • See Handout • Part A 1 – 33 odd • Part B 35 – 43 all