Conic Sections The Parabola 1 Introduction Consider a

Conic Sections The Parabola 1

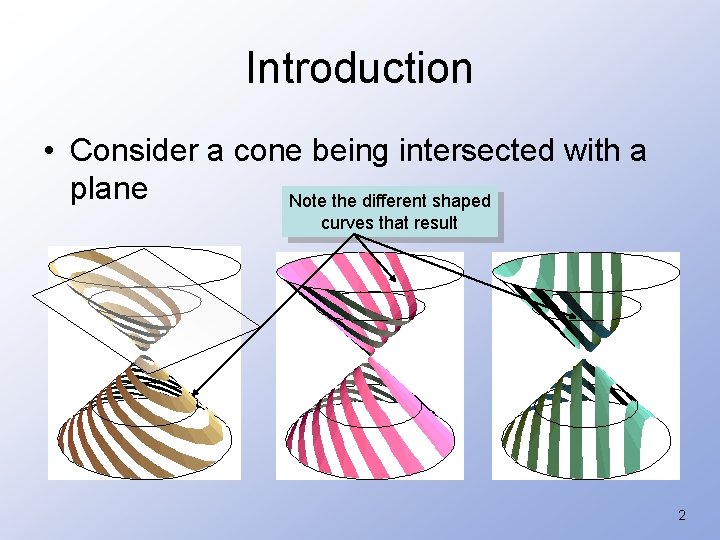
Introduction • Consider a cone being intersected with a plane Note the different shaped curves that result 2

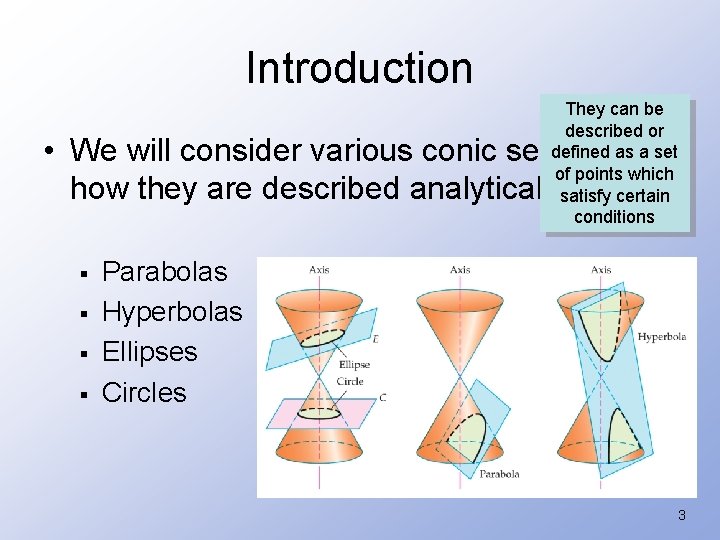
Introduction They can be described or defined as a set of points which satisfy certain conditions • We will consider various conic sections and how they are described analytically § § Parabolas Hyperbolas Ellipses Circles 3

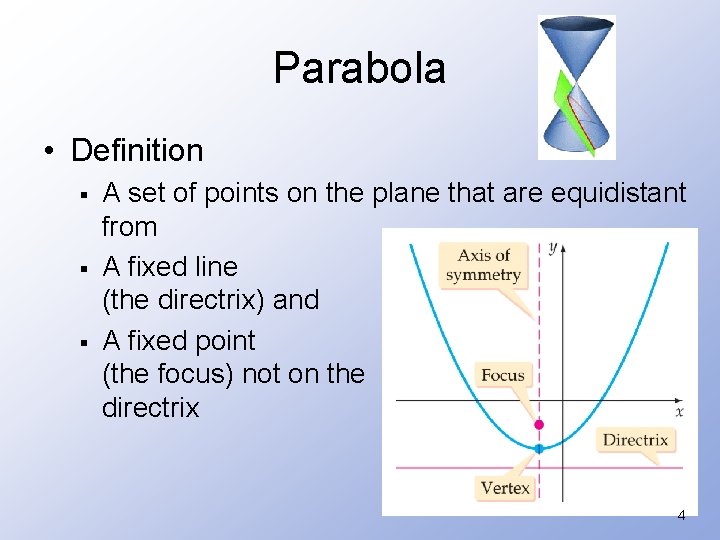
Parabola • Definition § § § A set of points on the plane that are equidistant from A fixed line (the directrix) and A fixed point (the focus) not on the directrix 4

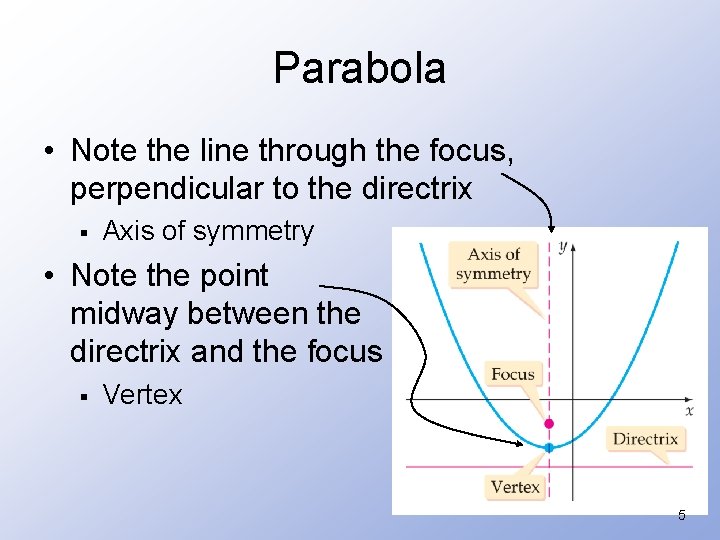
Parabola • Note the line through the focus, perpendicular to the directrix § Axis of symmetry • Note the point midway between the directrix and the focus § Vertex 5

Equation of Parabola • Let the vertex be at (0, 0) § § § Axis of symmetry be y-axis Directrix be the line y = -p (where p > 0) Focus is then at (0, p) • For any point (x, y) on the parabola Distance = y + p 6

Equation of Parabola • Setting the two distances equal to each other . . . simplifying. . . Link to web example • What happens if p < 0? • What happens if we have 7

Working with the Formula • Given the equation of a parabola § y = ½ x 2 • Determine § § The directrix The focus • Given the focus at (-3, 0) and the fact that the vertex is at the origin • Determine the equation 8

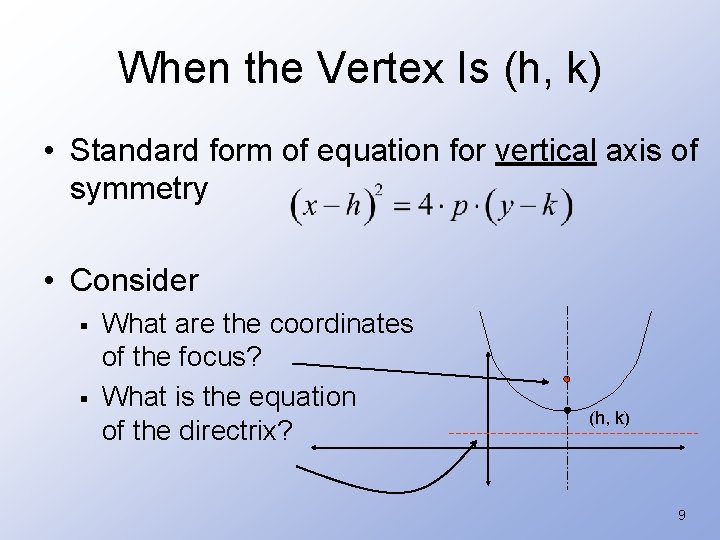
When the Vertex Is (h, k) • Standard form of equation for vertical axis of symmetry • Consider § § What are the coordinates of the focus? What is the equation of the directrix? (h, k) 9

When the Vertex Is (h, k) • Standard form of equation for horizontal axis of symmetry • Consider § § What are the coordinates of the focus? What is the equation of the directrix? (h, k) 10

Try It Out • Given the equations below, § § What is the focus? What is the directrix? 11

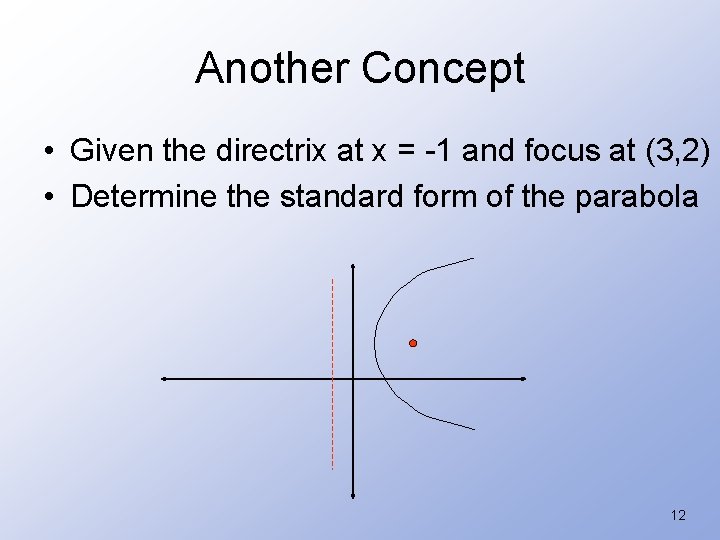
Another Concept • Given the directrix at x = -1 and focus at (3, 2) • Determine the standard form of the parabola 12

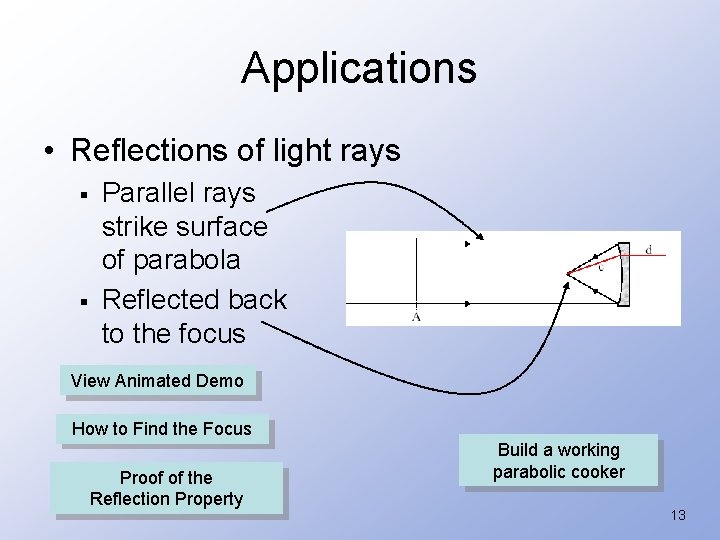
Applications • Reflections of light rays § § Parallel rays strike surface of parabola Reflected back to the focus View Animated Demo How to Find the Focus Proof of the Reflection Property Build a working parabolic cooker 13

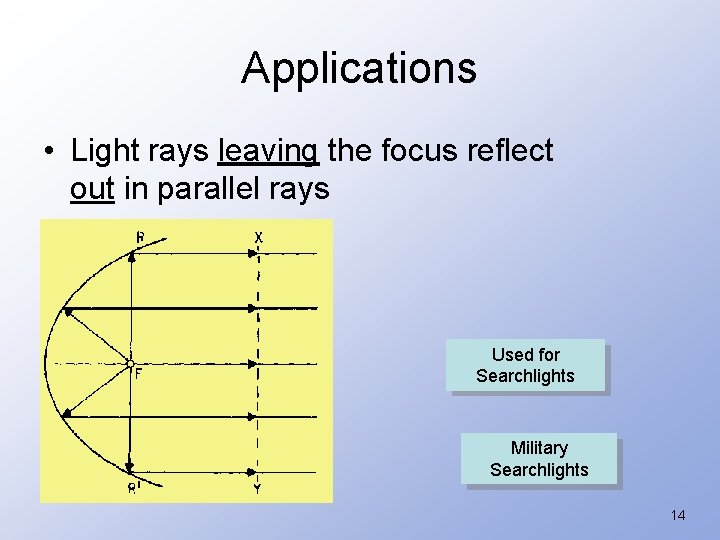
Applications • Light rays leaving the focus reflect out in parallel rays Used for Searchlights Military Searchlights 14

Assignment • See Handout • Part A 1 – 33 odd • Part B 35 – 43 all 15