Conic Sections Table of Contents Four Conic Sections

Conic Sections

Table of Contents Four Conic Sections Conics in a rectangle Sections of a right cone More Problems Focal Spheres Tangent to the Conics 1 The Conics in everyday life Tangents to the Conics 2 (HL) Terminology Double Hyperbola Conics as plane loci Common Properties Conics as plane loci - Problems Centre of Curvature & Evolute

FOUR CONIC SECTIONS

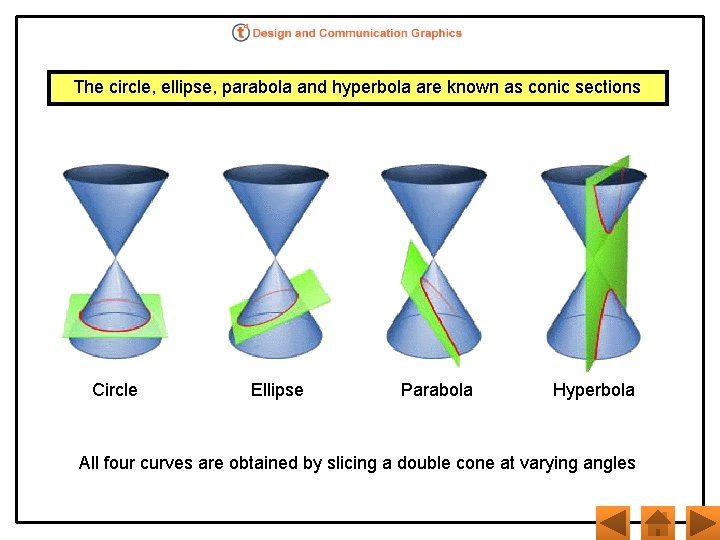
The circle, ellipse, parabola and hyperbola are known as conic sections Circle Ellipse Parabola Hyperbola All four curves are obtained by slicing a double cone at varying angles

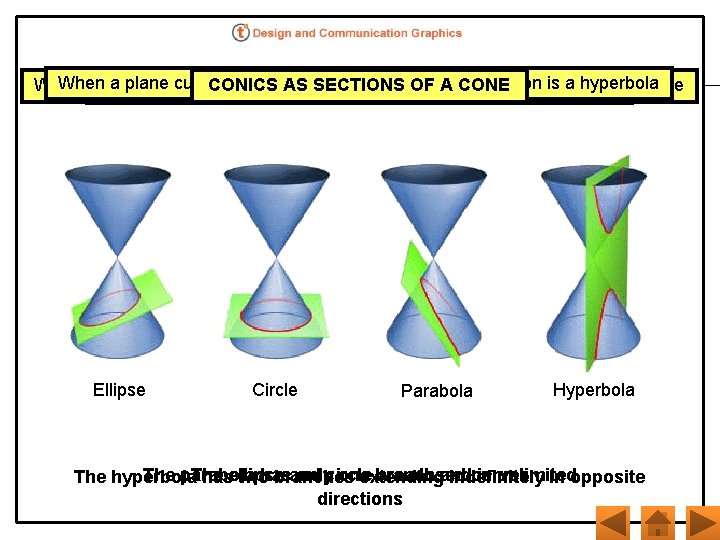
When a plane cuts both parts the double the section isparabola a circle hyperbola athis plane parallel toof one generator, the section ais When a. When plane cuts all is generators on one side theissection is an ellipse CONICS AS SECTIONS OF Aapex, CONE When plane is perpendicular to theofcone, axis, the section a Ellipse Circle Parabola Hyperbola The parabola has onlycircle one branch and is unlimited The and are closed curves The hyperbola hasellipse two branches extending indefinitely in opposite directions

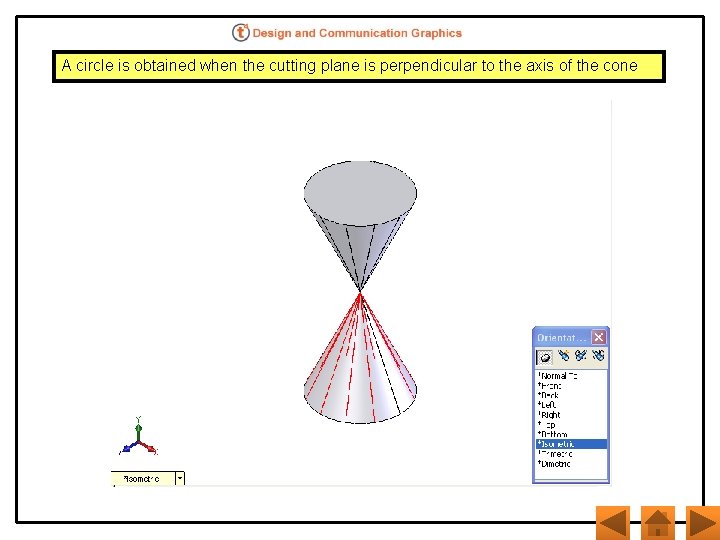
A circle is obtained when the cutting plane is perpendicular to the axis of the cone

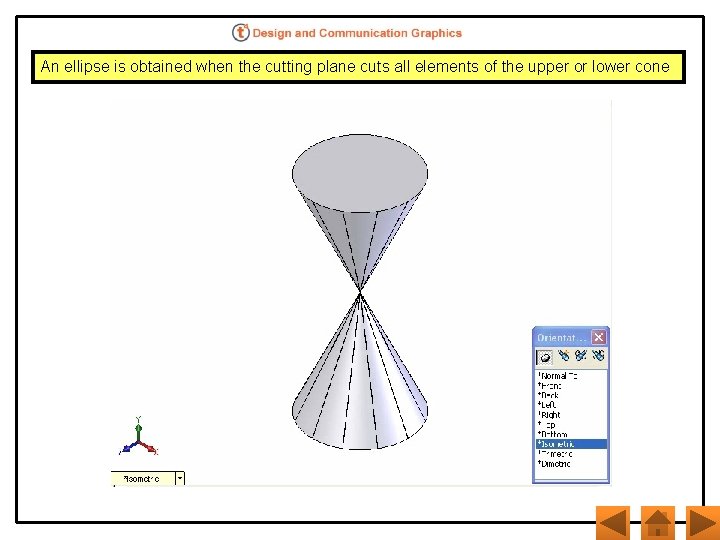
An ellipse is obtained when the cutting plane cuts all elements of the upper or lower cone

A parabola is obtained when the cutting plane is parallel to a generating line

A hyperbola is obtained when the cutting plane cuts both the upper and lower cones

THE ELLIPSE AROUND US q The circle is the simplest of all curves q However, the ellipse is the curve most often "seen" in everyday life q This is because every circle, viewed obliquely, appears elliptical q The orbits of the planets are ellipses

THE PARABOLA AROUND US When a sliothar or golf ball is hit into the air, it follows a parabolic path The centre of gravity of a leaping salmon describes a parabola The parabola is used by engineers in designing some suspension bridges

THE HYPERBOLA AROUND US A hyperbola is formed when a right circular cone is intersected by a plane parallel to its axis Such an intersection occurs in physical situations as simple as sharpening a pencil that has a polygonal cross section………. …. . . and in the patterns formed on a floor by a flash light

SECTIONS OF A RIGHT CONE

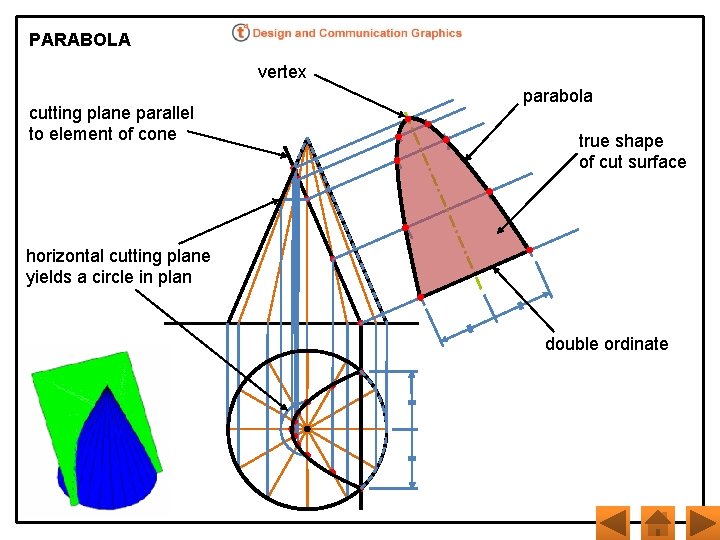
PARABOLA vertex cutting plane parallel to element of cone parabola true shape of cut surface horizontal cutting plane yields a circle in plan double ordinate

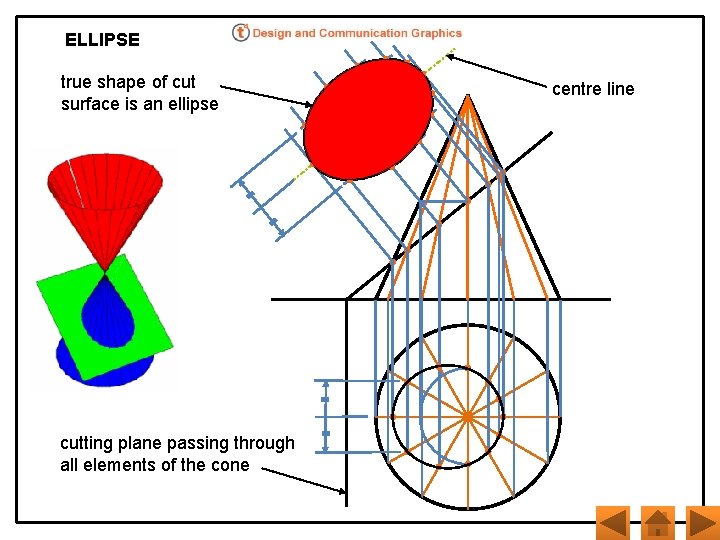
ELLIPSE true shape of cut surface is an ellipse cutting plane passing through all elements of the cone centre line

ELLIPSE File - 24. swf

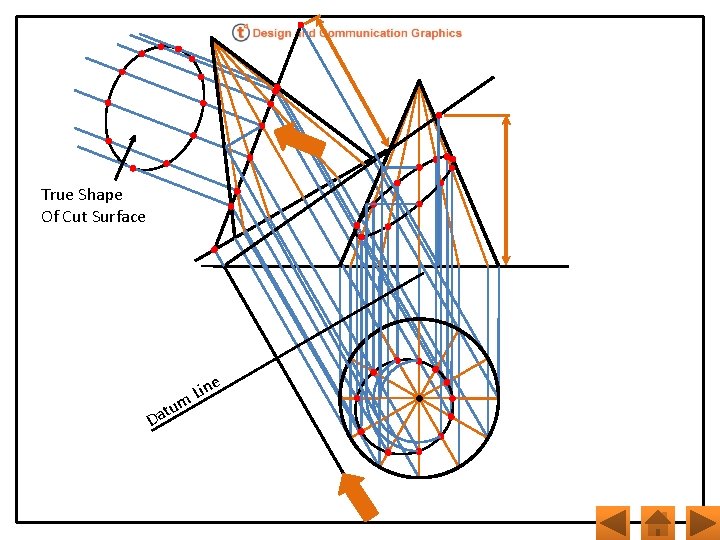
True Shape Of Cut Surface m tu Da e Lin

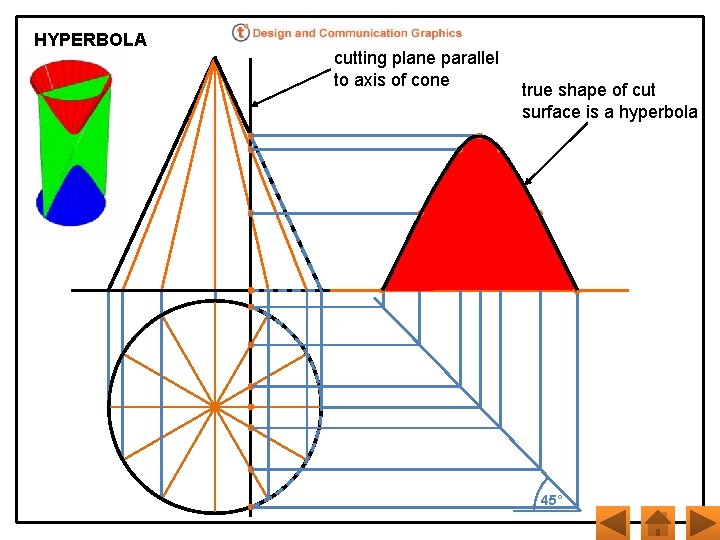
HYPERBOLA cutting plane parallel to axis of cone true shape of cut surface is a hyperbola 45°

FOCAL SPHERES

TERMINOLOGY Ø A focal sphere is a sphere inscribed in the cone tangential to the cutting plane Ø The focus is the point of contact between the sphere and the cutting plane Ø The directrix is the line of intersection between the cutting plane and the horizontal plane through the tangent circle of the sphere and cone Ø The axis is a line through the focus perpendicular to the directrix Ø The vertex is the point in which the curve intersects the axis

FOCAL SPHERE FOR A PARABOLA File Parabola. EPRT

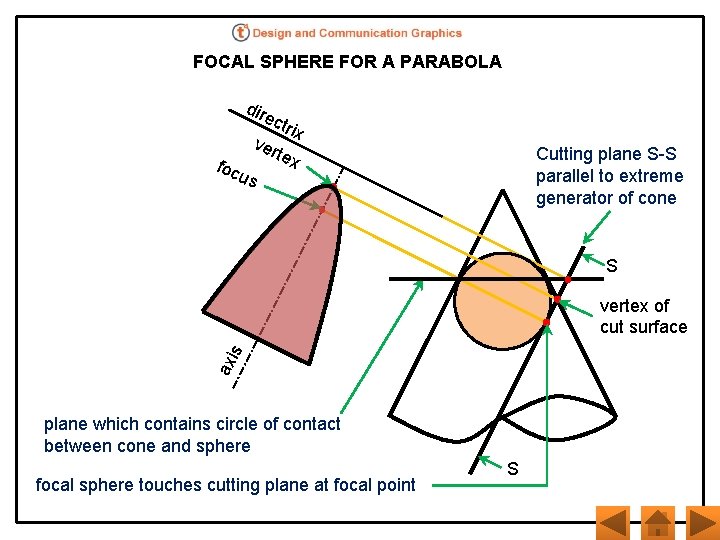
FOCAL SPHERE FOR A PARABOLA dir ect rix ver tex foc us Cutting plane S-S parallel to extreme generator of cone S axi s vertex of cut surface plane which contains circle of contact between cone and sphere focal sphere touches cutting plane at focal point S

FOCAL SPHERES FOR AN ELLIPSE File - Ellipse. EPRT

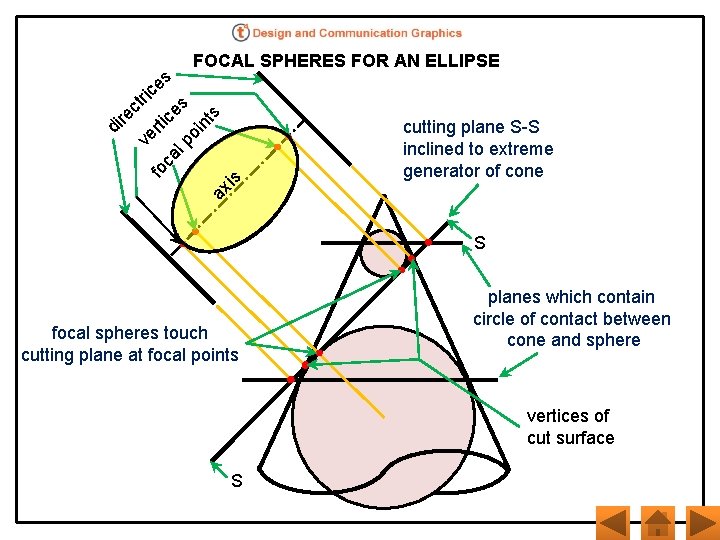
fo c s al po in t s e ric s t c ce re i i t r d ve FOCAL SPHERES FOR AN ELLIPSE i x a s cutting plane S-S inclined to extreme generator of cone S focal spheres touch cutting plane at focal points planes which contain circle of contact between cone and sphere vertices of cut surface S

FOCAL SPHERE FOR A HYPERBOLA File - Hyperbola. EPRT

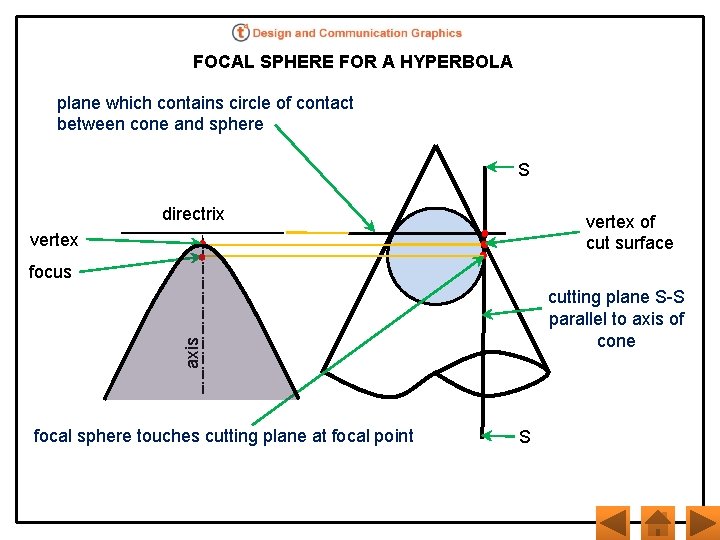
FOCAL SPHERE FOR A HYPERBOLA plane which contains circle of contact between cone and sphere S directrix vertex of cut surface vertex focus axis cutting plane S-S parallel to axis of cone focal sphere touches cutting plane at focal point S

THE CONICS IN EVERYDAY LIFE

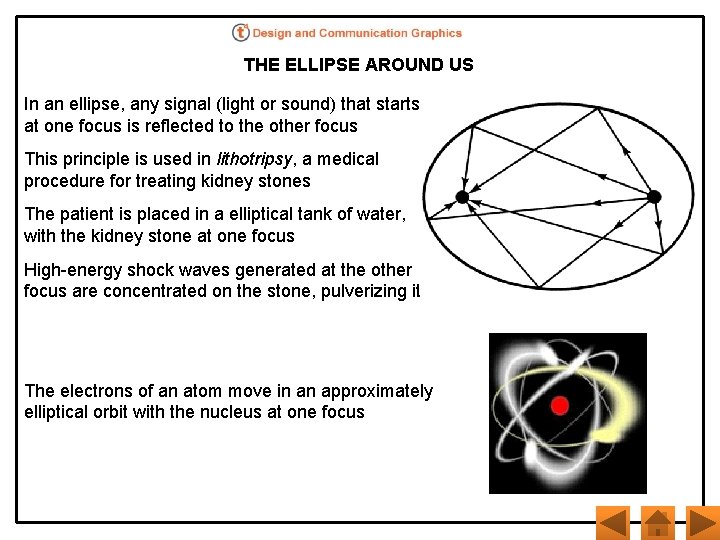
THE ELLIPSE AROUND US In an ellipse, any signal (light or sound) that starts at one focus is reflected to the other focus This principle is used in lithotripsy, a medical procedure for treating kidney stones The patient is placed in a elliptical tank of water, with the kidney stone at one focus High-energy shock waves generated at the other focus are concentrated on the stone, pulverizing it The electrons of an atom move in an approximately elliptical orbit with the nucleus at one focus

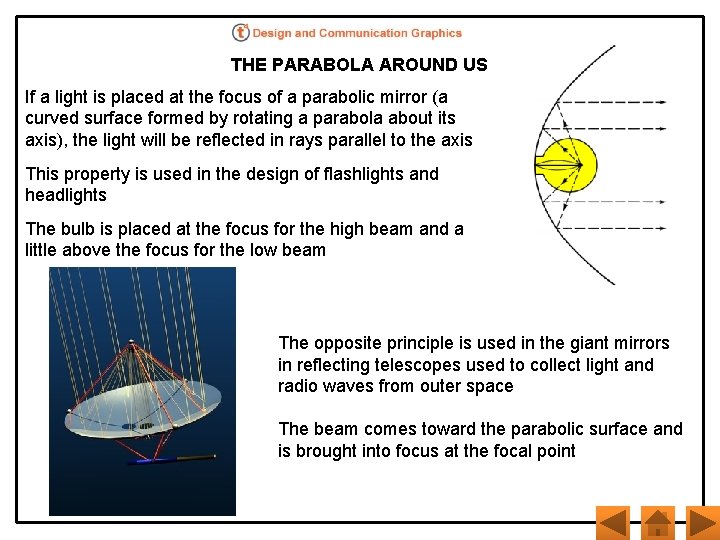
THE PARABOLA AROUND US If a light is placed at the focus of a parabolic mirror (a curved surface formed by rotating a parabola about its axis), the light will be reflected in rays parallel to the axis This property is used in the design of flashlights and headlights The bulb is placed at the focus for the high beam and a little above the focus for the low beam The opposite principle is used in the giant mirrors in reflecting telescopes used to collect light and radio waves from outer space The beam comes toward the parabolic surface and is brought into focus at the focal point

THE HYPERBOLA AROUND US ü The path of a comet often takes the shape of a hyperbola ü Many telescopes use hyperbolic (hyperbola-shaped) lenses ü Sound waves travel in hyperbolic paths, and so there applications of the hyperbola in navigation (GPS systems) ü The hyperbolic shape of water cooling towers helps the tower do its job more efficiently

TERMINOLOGY

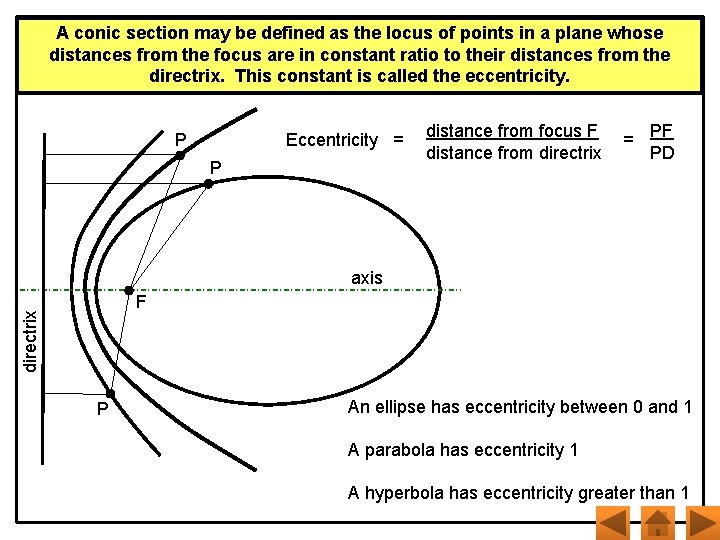
A conic section may be defined as the locus of points in a plane whose distances from the focus are in constant ratio to their distances from the directrix. This constant is called the eccentricity. Eccentricity = P P distance from focus F distance from directrix = PF PD axis directrix F P An ellipse has eccentricity between 0 and 1 A parabola has eccentricity 1 A hyperbola has eccentricity greater than 1

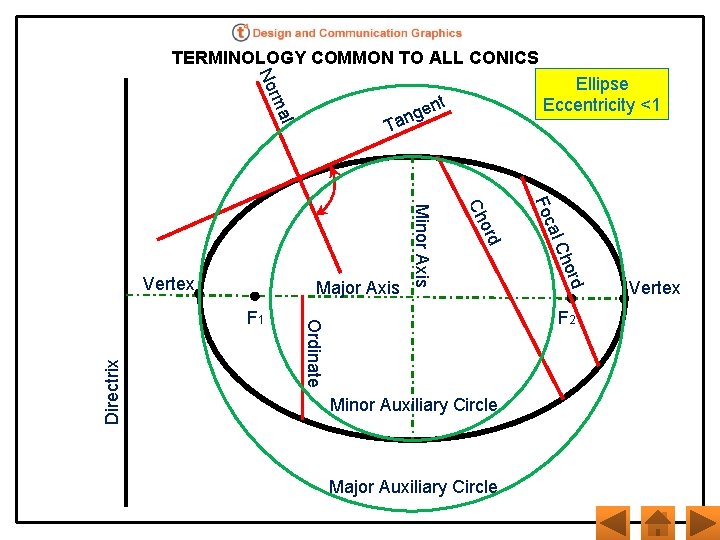
TERMINOLOGY COMMON TO ALL CONICS No t rma T l d hor al C Foc ord Ch Major Axis F 2 Ordinate F 1 Directrix en g n a Minor Axis Vertex Ellipse Eccentricity <1 Minor Auxiliary Circle Major Auxiliary Circle Vertex

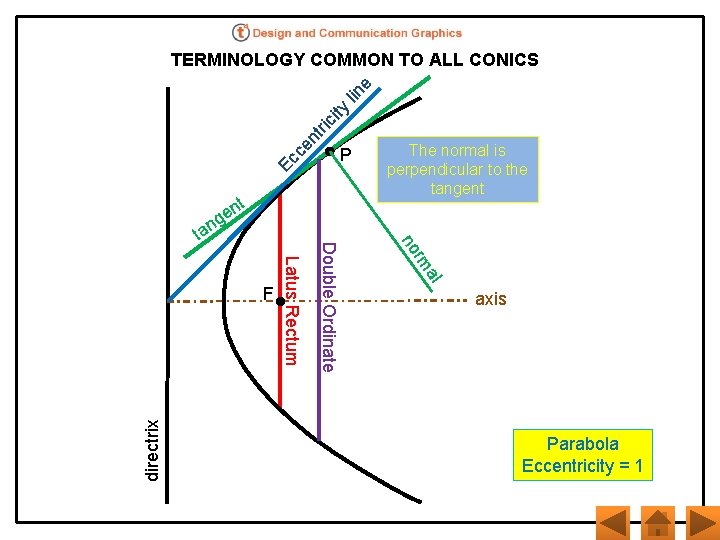
Ec ce n tri ci ty lin e TERMINOLOGY COMMON TO ALL CONICS al rm directrix The normal is perpendicular to the tangent no Latus Rectum F Double Ordinate nt e g n a t P axis Parabola Eccentricity = 1

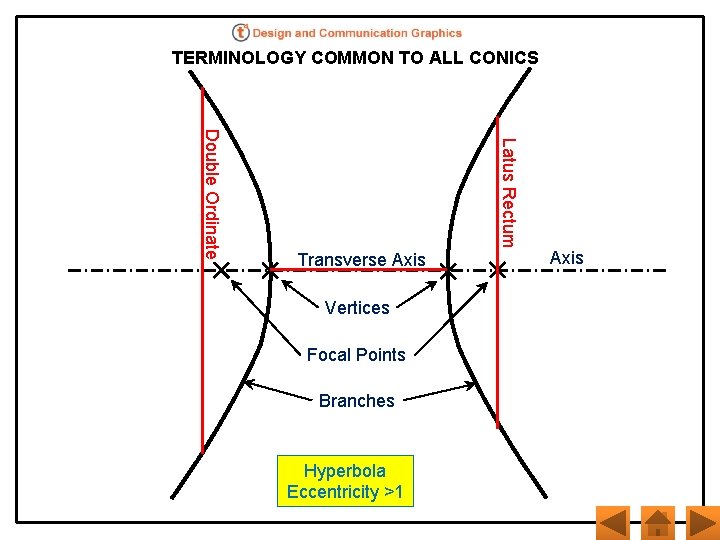
TERMINOLOGY COMMON TO ALL CONICS Latus Rectum Double Ordinate Transverse Axis Vertices Focal Points Branches Hyperbola Eccentricity >1 Axis

ELLIPSE CONICS AS PLANE LOCI

The directrix and focal point of a parabola are shown. Locate the vertex and draw a portion of the curve axis directrix F

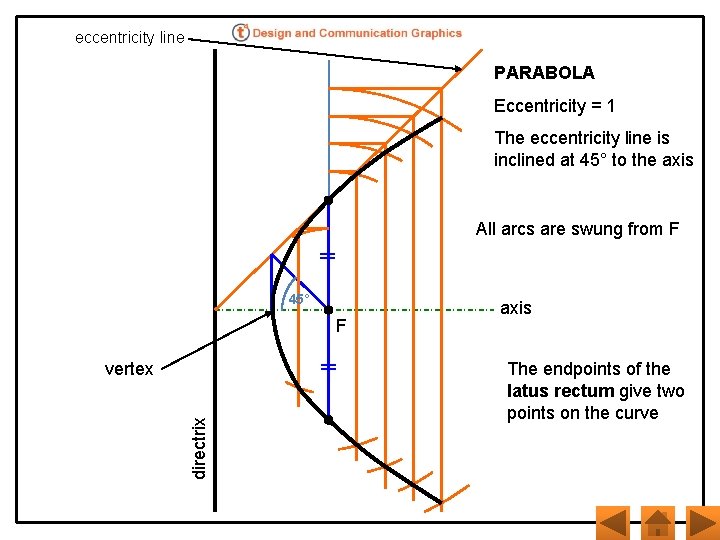
eccentricity line PARABOLA Eccentricity = 1 The eccentricity line is inclined at 45° to the axis All arcs are swung from F 45° F directrix vertex axis The endpoints of the latus rectum give two points on the curve

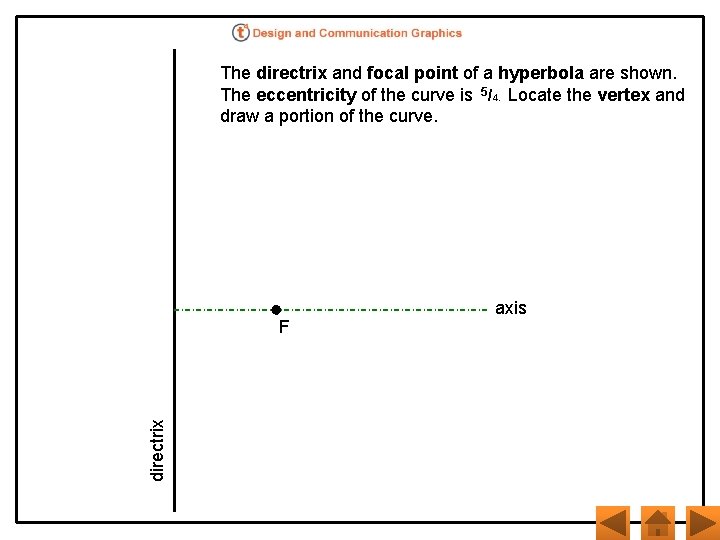
The directrix and focal point of a hyperbola are shown. The eccentricity of the curve is 5/4. Locate the vertex and draw a portion of the curve. directrix F axis

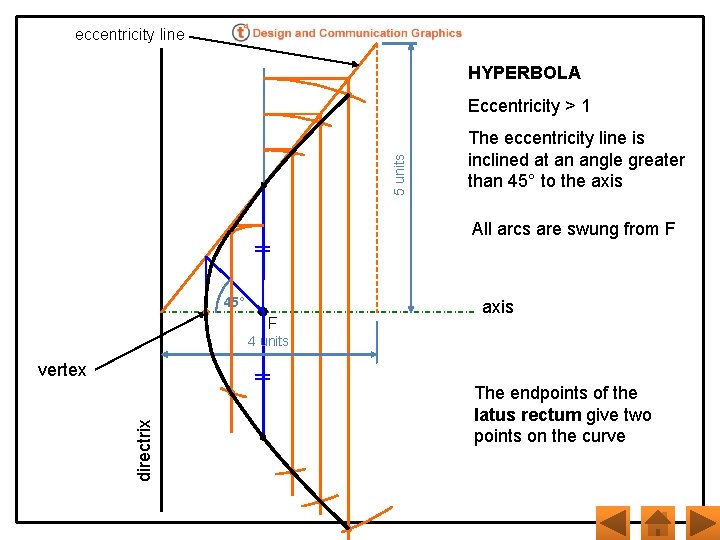
eccentricity line HYPERBOLA 5 units Eccentricity > 1 The eccentricity line is inclined at an angle greater than 45° to the axis All arcs are swung from F 45° F axis 4 units directrix vertex The endpoints of the latus rectum give two points on the curve

The directrix and focal point of an ellipse are shown. The eccentricity of the curve is 3/4. Locate the vertex and draw a portion of the curve. directrix F axis

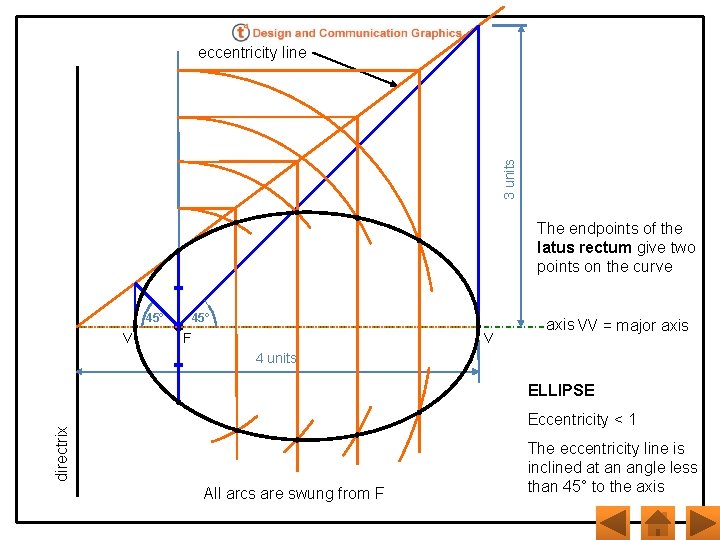
3 units eccentricity line The endpoints of the latus rectum give two points on the curve 45° V 45° F V axis VV = major axis 4 units ELLIPSE directrix Eccentricity < 1 All arcs are swung from F The eccentricity line is inclined at an angle less than 45° to the axis

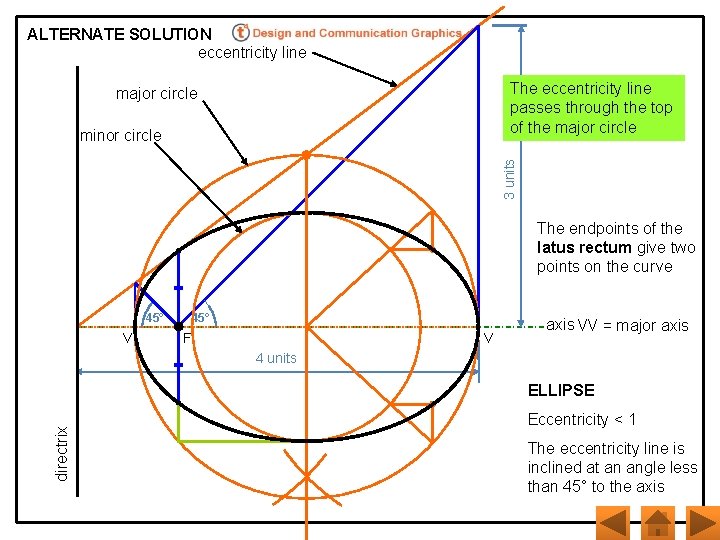
ALTERNATE SOLUTION eccentricity line The eccentricity line passes through the top of the major circle 3 units minor circle The endpoints of the latus rectum give two points on the curve 45° V 45° F V axis VV = major axis 4 units directrix ELLIPSE Eccentricity < 1 The eccentricity line is inclined at an angle less than 45° to the axis

CONICS AS PLANE LOCI - PROBLEMS

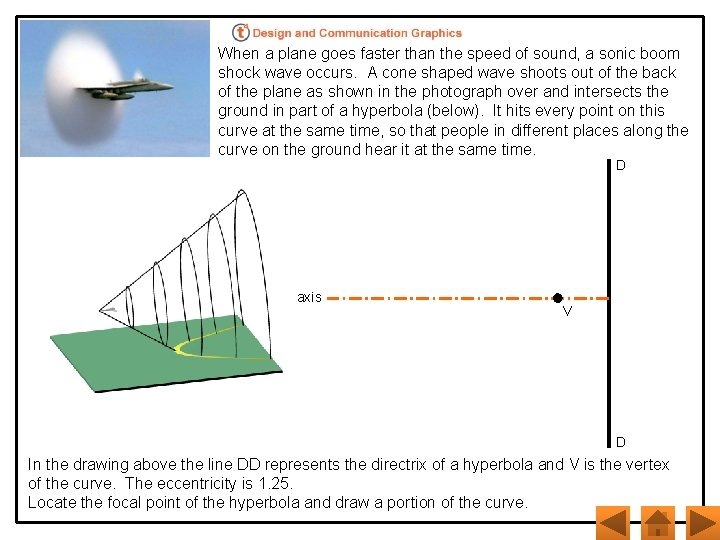
When a plane goes faster than the speed of sound, a sonic boom shock wave occurs. A cone shaped wave shoots out of the back of the plane as shown in the photograph over and intersects the ground in part of a hyperbola (below). It hits every point on this curve at the same time, so that people in different places along the curve on the ground hear it at the same time. D axis V D In the drawing above the line DD represents the directrix of a hyperbola and V is the vertex of the curve. The eccentricity is 1. 25. Locate the focal point of the hyperbola and draw a portion of the curve.

When a pencil that has a hexagonal cross section is sharpened, a hyperbola is formed. This results from the intersection of the conical point of the pencil by one of its flat sides. Two lines VF and FD are shown in the drawing below. V is the vertex of a hyperbola, F is a focal point of the curve and D is a point on the directrix. Locate the directrix and eccentricity line and draw a portion of the curve. D V F

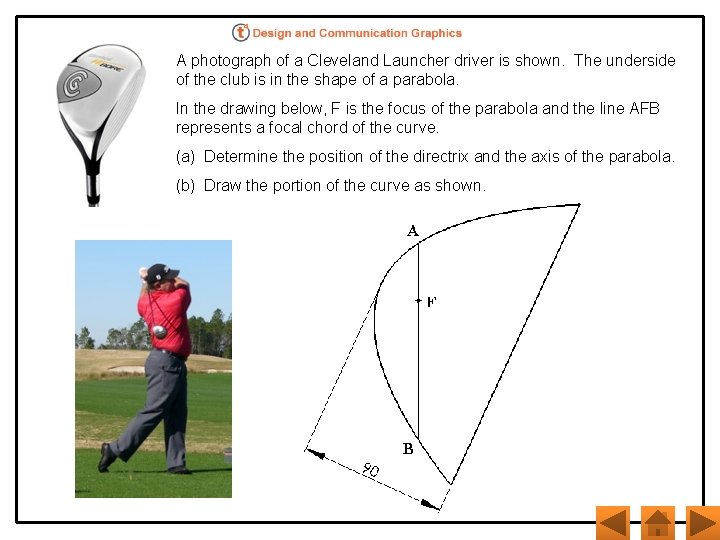
A photograph of a Cleveland Launcher driver is shown. The underside of the club is in the shape of a parabola. In the drawing below, F is the focus of the parabola and the line AFB represents a focal chord of the curve. (a) Determine the position of the directrix and the axis of the parabola. (b) Draw the portion of the curve as shown.

ELLIPSE CONICS IN A RECTANGLE

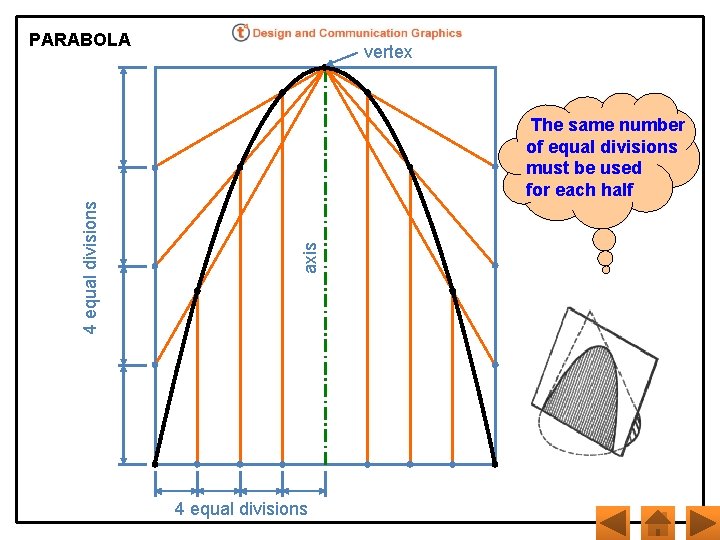
PARABOLA vertex axis 4 equal divisions The same number of equal divisions must be used for each half 4 equal divisions

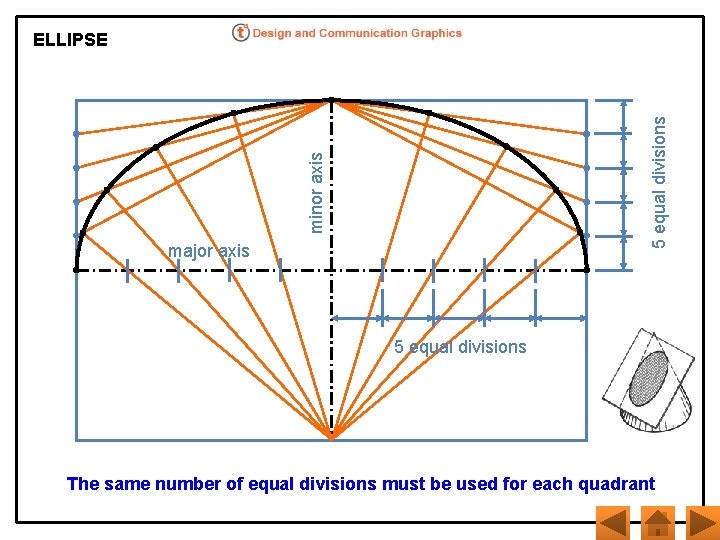
minor axis 5 equal divisions ELLIPSE major axis 5 equal divisions The same number of equal divisions must be used for each quadrant

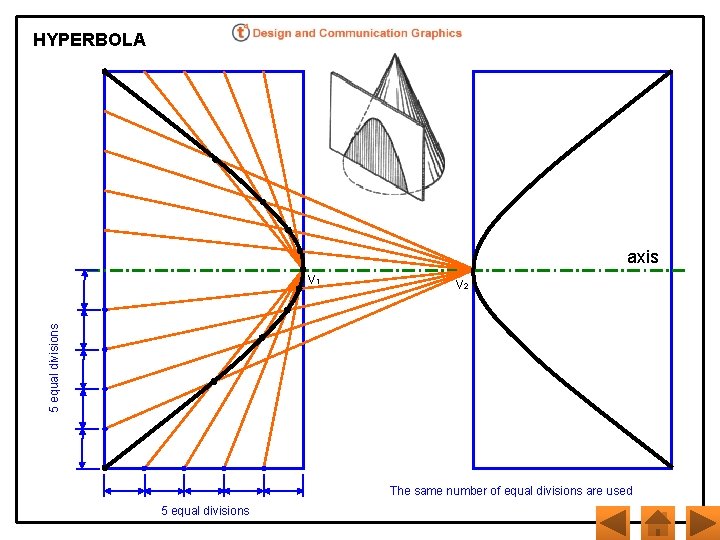
HYPERBOLA axis V 2 5 equal divisions V 1 The same number of equal divisions are used 5 equal divisions

MORE PROBLEMS

A photograph of a Parabola Hall Table designed by Nathan Hunter is shown. Two curly wood panels intersect steel parabolas to support a glass top. The curved panels are portions of an ellipse. The incomplete elevation of the table is given over. The two parabolas are to be inscribed in the rectangles ABCD and EFGH, respectively. P is a point on the curve of the ellipse whose minor axis MN is drawn. Complete the view of the hall table showing all construction lines.

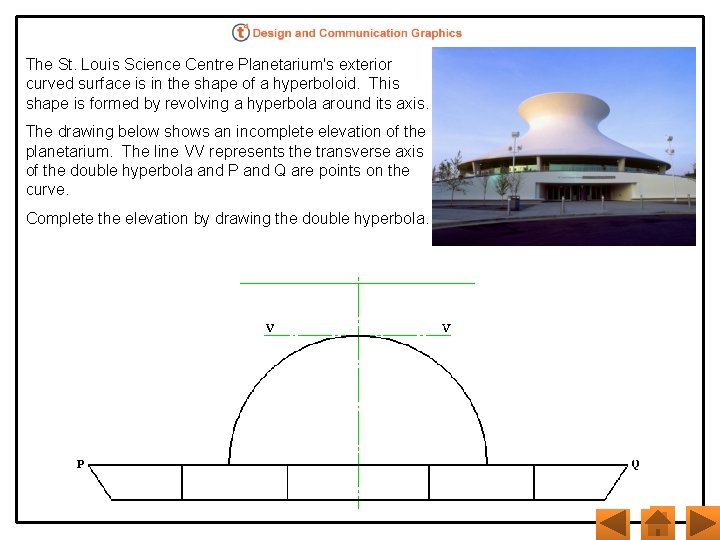
The St. Louis Science Centre Planetarium's exterior curved surface is in the shape of a hyperboloid. This shape is formed by revolving a hyperbola around its axis. The drawing below shows an incomplete elevation of the planetarium. The line VV represents the transverse axis of the double hyperbola and P and Q are points on the curve. Complete the elevation by drawing the double hyperbola.

TANGENTS TO THE CONICS 1

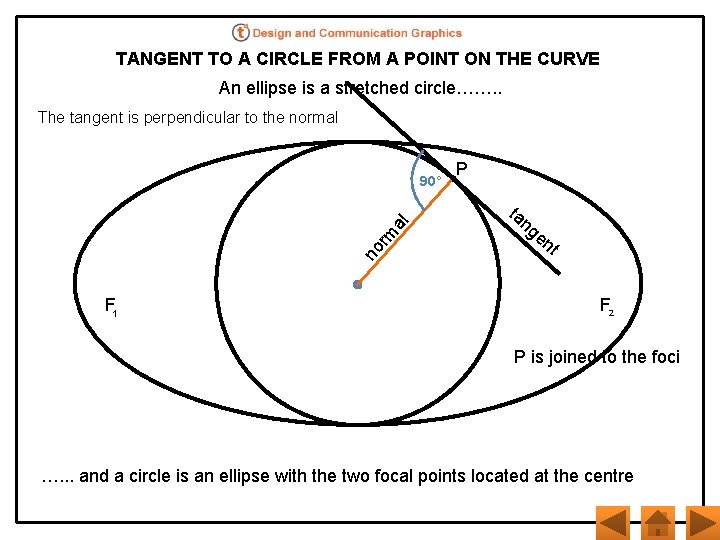
TANGENT TO A CIRCLE FROM A POINT ON THE CURVE An ellipse is a stretched circle……. . The tangent is perpendicular to the normal no rm al 90° F 1 P ta ng e nt F 2 P is joined to the foci …. . . and a circle is an ellipse with the two focal points located at the centre

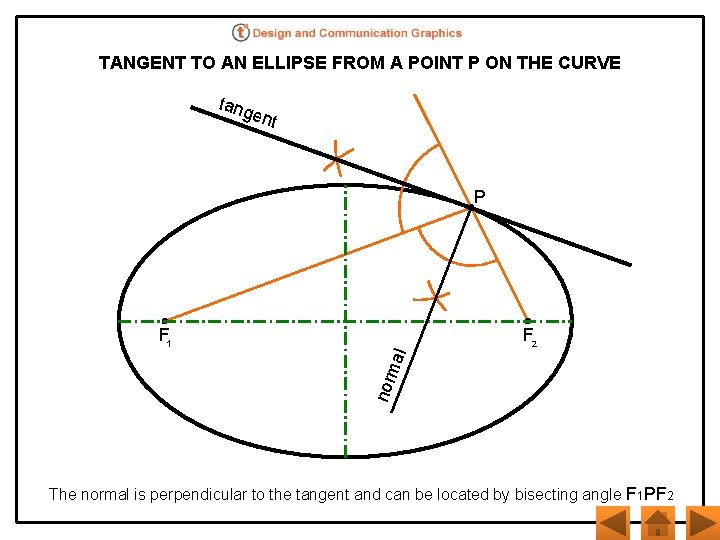
TANGENT TO AN ELLIPSE FROM A POINT P ON THE CURVE tang ent P F 2 nor mal F 1 The normal is perpendicular to the tangent and can be located by bisecting angle F 1 PF 2

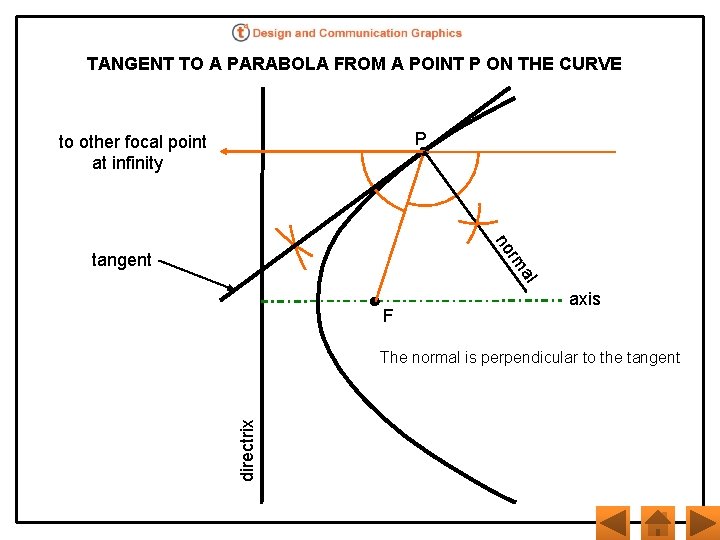
TANGENT TO A PARABOLA FROM A POINT P ON THE CURVE P to other focal point at infinity rm no tangent al F axis directrix The normal is perpendicular to the tangent

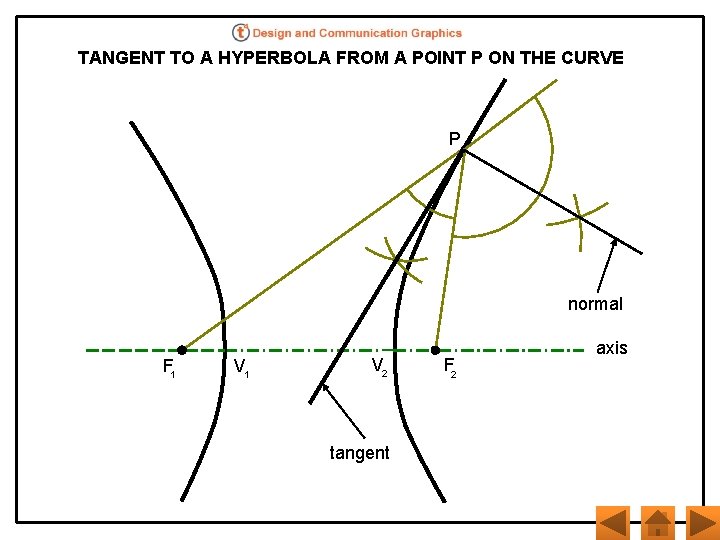
TANGENT TO A HYPERBOLA FROM A POINT P ON THE CURVE P normal F 1 V 2 tangent F 2 axis

TANGENTS TO THE CONICS 2 (HIGHER LEVEL)

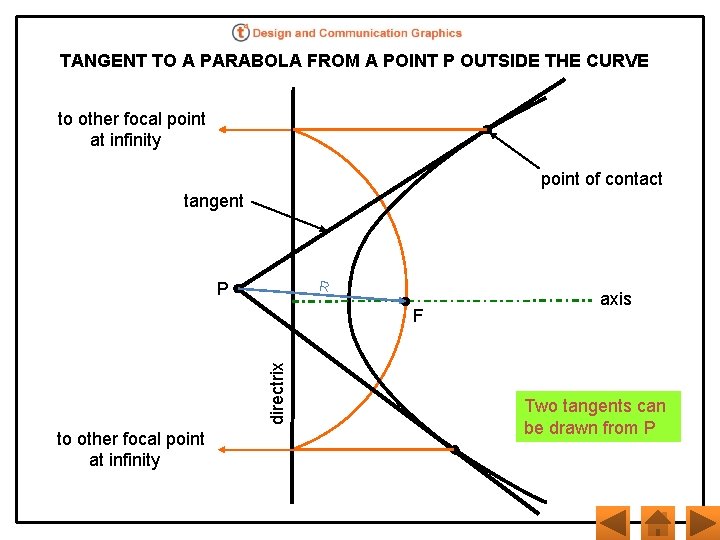
TANGENT TO A PARABOLA FROM A POINT P OUTSIDE THE CURVE to other focal point at infinity point of contact tangent P R directrix F to other focal point at infinity axis Two tangents can be drawn from P

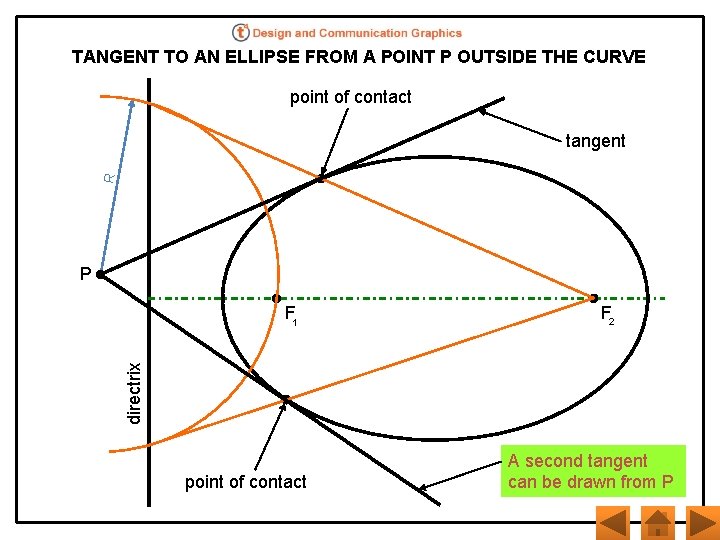
TANGENT TO AN ELLIPSE FROM A POINT P OUTSIDE THE CURVE point of contact R tangent P F 2 directrix F 1 point of contact A second tangent can be drawn from P

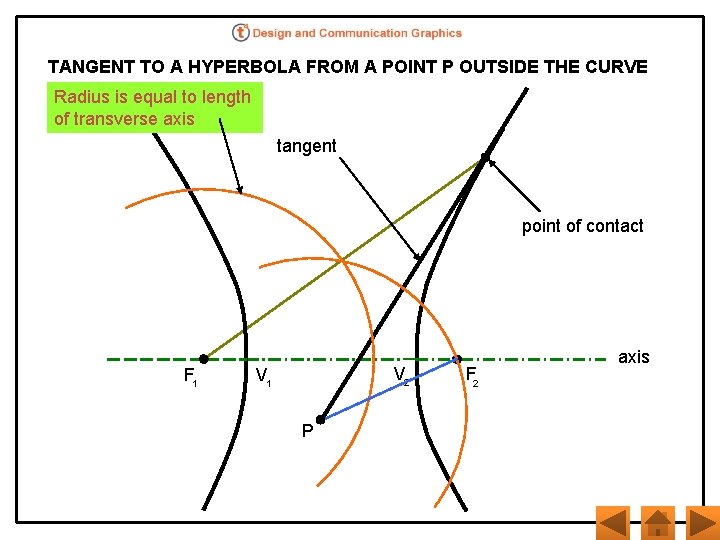
TANGENT TO A HYPERBOLA FROM A POINT P OUTSIDE THE CURVE Radius is equal to length of transverse axis tangent point of contact F 1 V 2 V 1 P F 2 axis

DOUBLE HYPERBOLA FROM FOCI AND TRANSVERSE AXIS

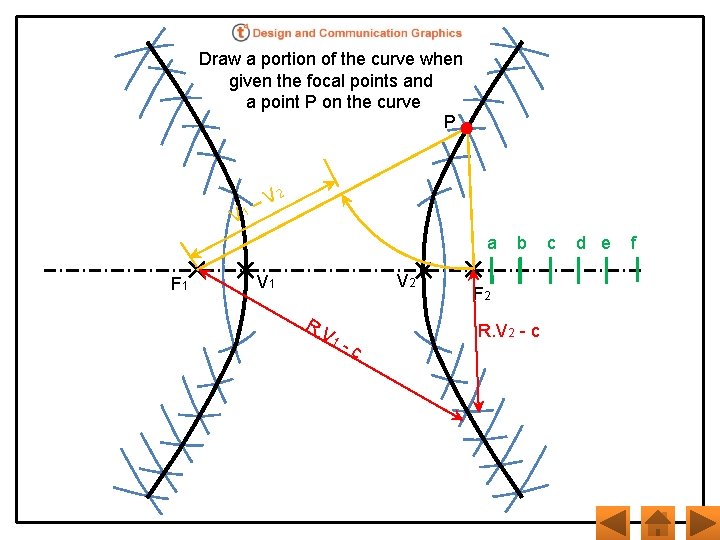
Draw a portion of the curve when given the focal points and a point P on the curve P V V 1– 2 a F 1 V 2 V 1 R. V 1 -c b F 2 R. V 2 - c c d e f

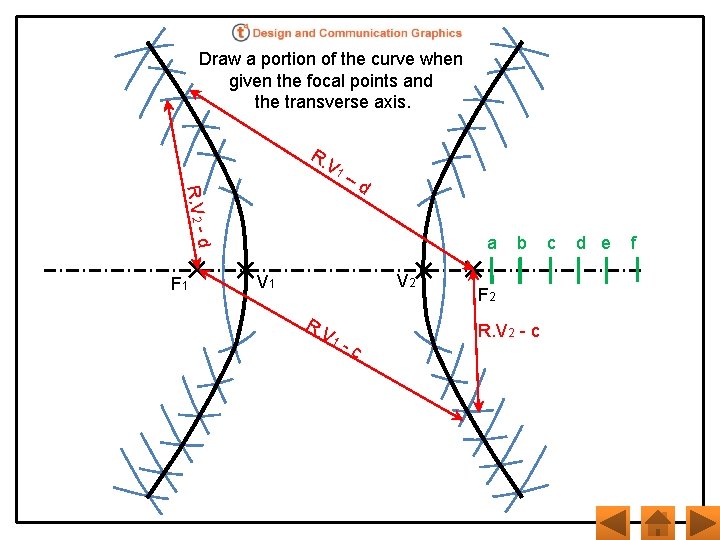
Draw a portion of the curve when given the focal points and the transverse axis. R. V 1 R. V 2 - –d d a F 1 V 2 V 1 R. V 1 -c b F 2 R. V 2 - c c d e f

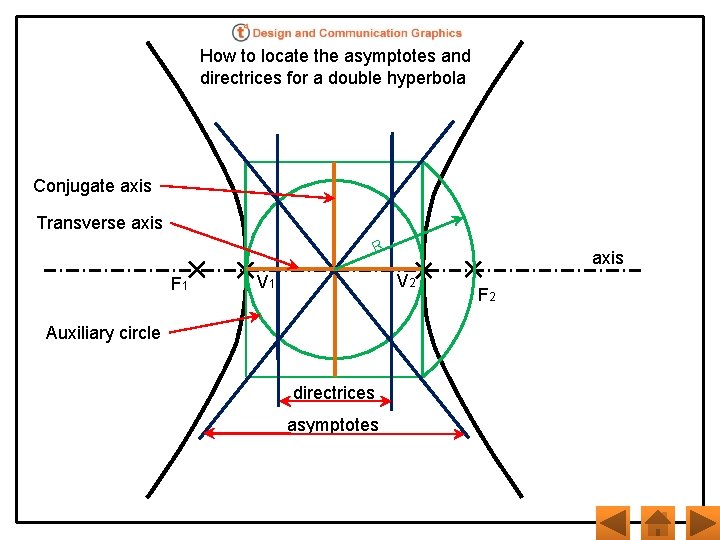
How to locate the asymptotes and directrices for a double hyperbola Conjugate axis Transverse axis R F 1 axis V 2 V 1 Auxiliary circle directrices asymptotes F 2

PROPERTIES COMMON TO ALL CONICS

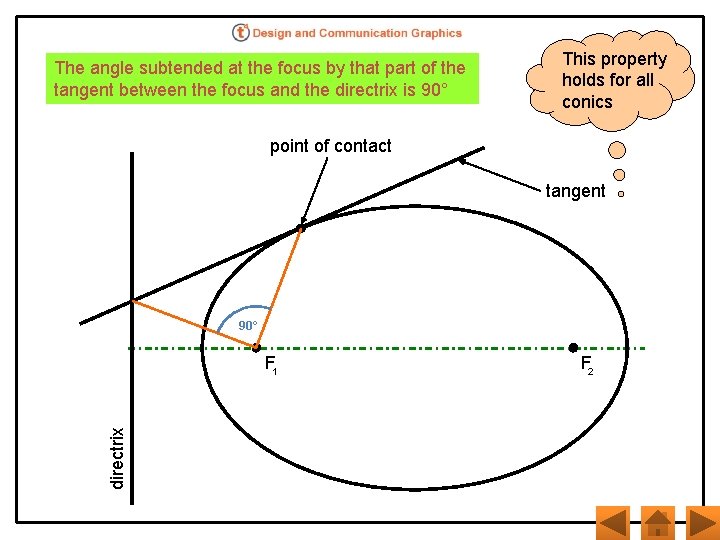
The angle subtended at the focus by that part of the tangent between the focus and the directrix is 90° This property holds for all conics point of contact tangent 90° directrix F 1 F 2

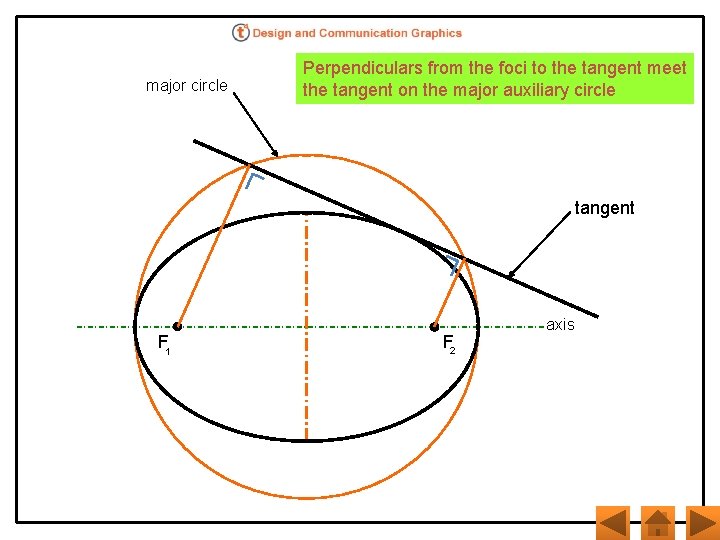
major circle Perpendiculars from the foci to the tangent meet the tangent on the major auxiliary circle tangent F 1 F 2 axis

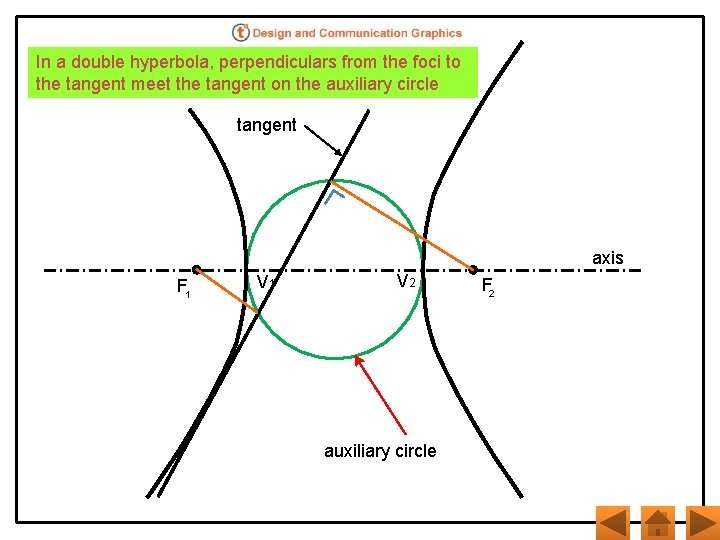
In a double hyperbola, perpendiculars from the foci to the tangent meet the tangent on the auxiliary circle tangent axis F 1 V 2 auxiliary circle F 2

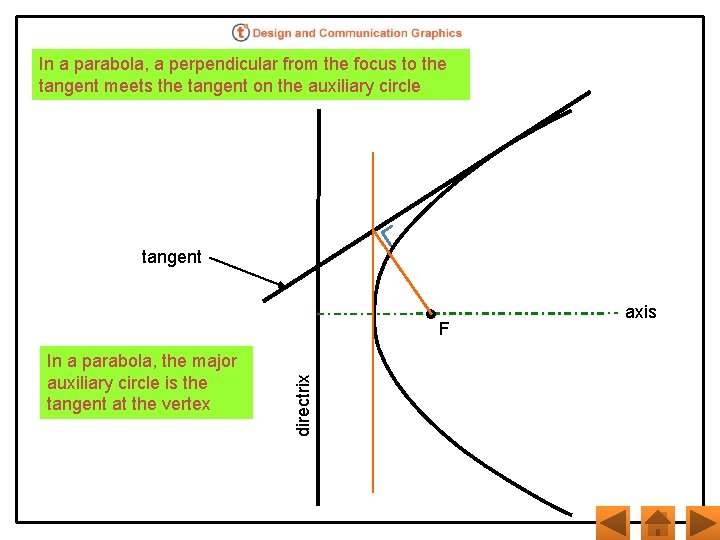
In a parabola, a perpendicular from the focus to the tangent meets the tangent on the auxiliary circle tangent In a parabola, the major auxiliary circle is the tangent at the vertex directrix F axis

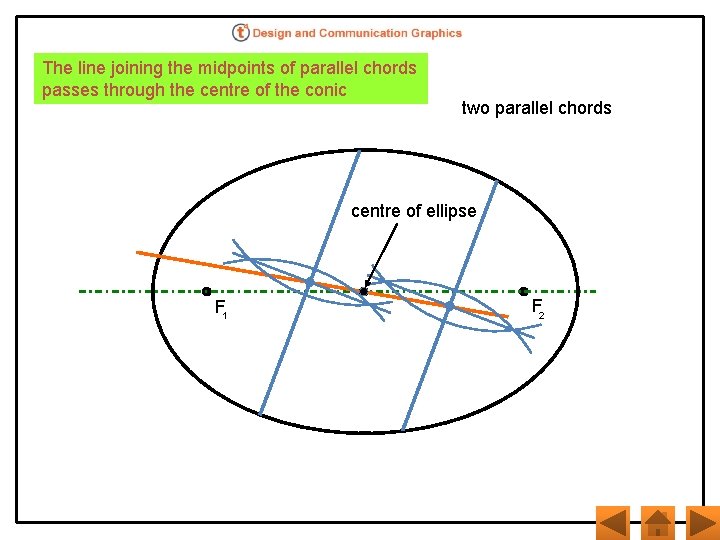
The line joining the midpoints of parallel chords passes through the centre of the conic two parallel chords centre of ellipse F 1 F 2

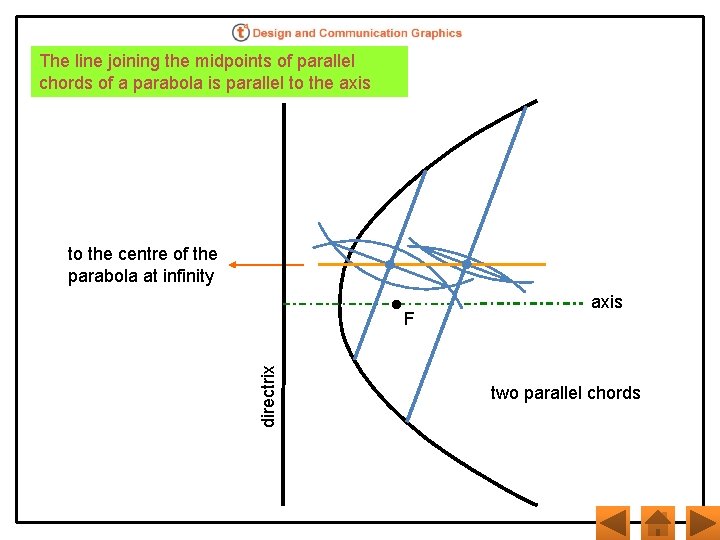
The line joining the midpoints of parallel chords of a parabola is parallel to the axis to the centre of the parabola at infinity directrix F axis two parallel chords

CENTRE OF CURVATURE & EVOLUTE

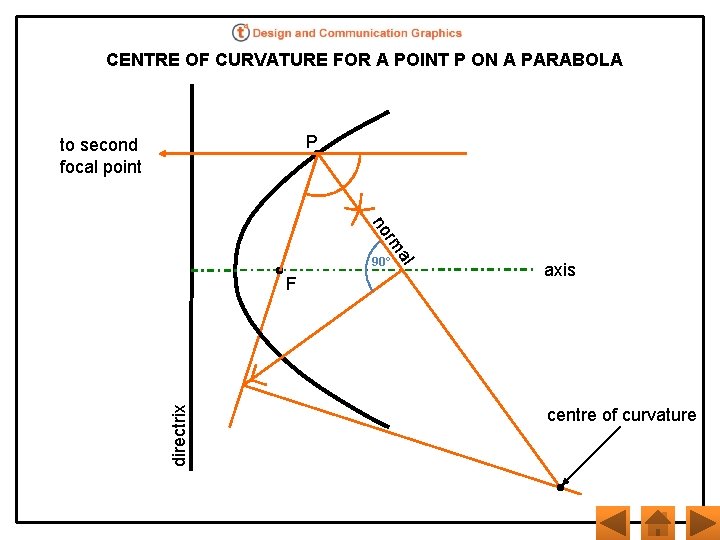
CENTRE OF CURVATURE FOR A POINT P ON A PARABOLA P to second focal point no directrix F al rm 90° axis centre of curvature

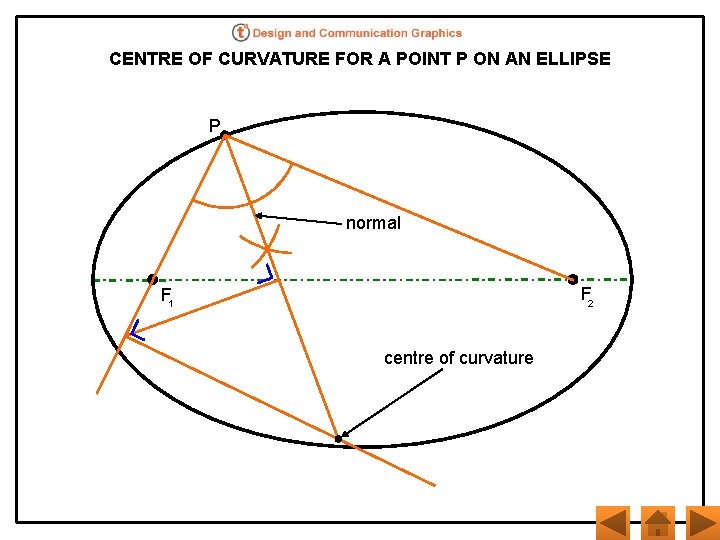
CENTRE OF CURVATURE FOR A POINT P ON AN ELLIPSE P normal F 2 F 1 centre of curvature

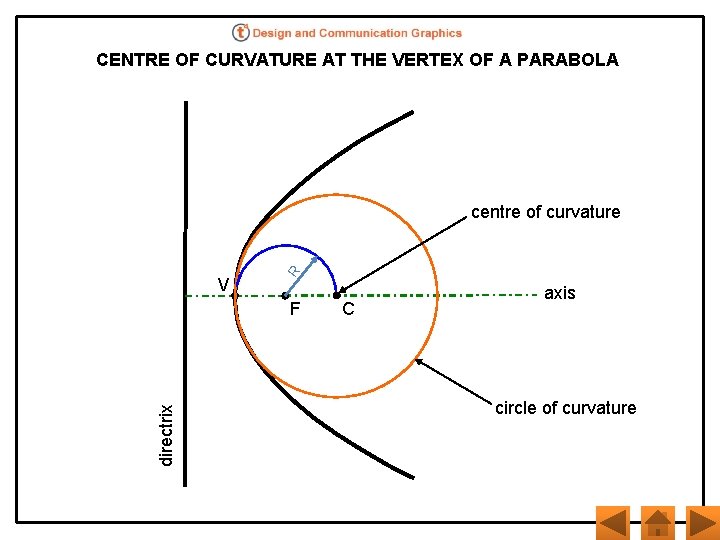
CENTRE OF CURVATURE AT THE VERTEX OF A PARABOLA V R centre of curvature directrix F C axis circle of curvature

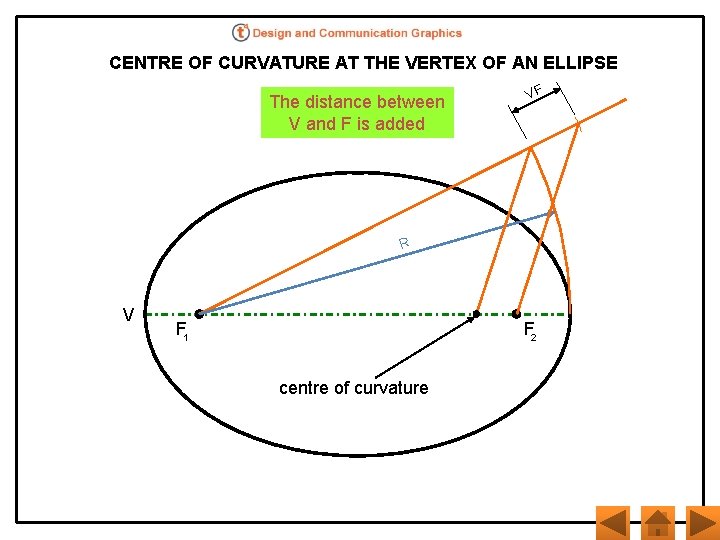
CENTRE OF CURVATURE AT THE VERTEX OF AN ELLIPSE The distance between V and F is added VF R V F 2 F 1 centre of curvature

CENTRE OF CURVATURE AT THE VERTEX OF A HYPERBOLA The distance between V and F is added VF R F 1 V V centre of curvature F 2

EVOLUTE OF A CONIC The evolute of a conic is the locus of its centre of curvature To construct an evolute: Ø Determine the centres of curvatures for a number of points on the curve Ø The points should include the vertices of the conic Ø Plot a curve through them

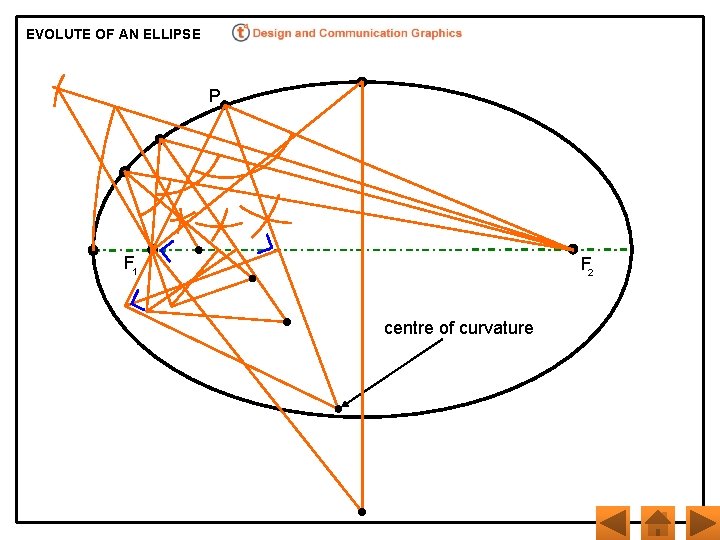
EVOLUTE OF AN ELLIPSE P F 1 F 2 centre of curvature

The evolute of an ellipse looks like this……… F 1 F 2

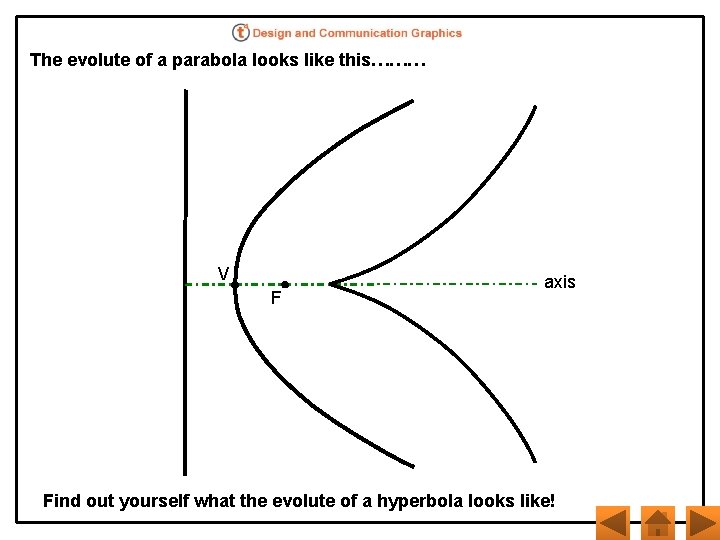
The evolute of a parabola looks like this……… V F axis Find out yourself what the evolute of a hyperbola looks like!