Conic Sections Dr Shildneck Conic Sections A conic

Conic Sections Dr. Shildneck

Conic Sections A conic section (or conic) is the intersection of a plane and a double-napped cone. There are four basic conic sections that we will study. • • The Circle The Ellipse The Parabola The Hyperbola

Degenerate Conics When a plane passes through the vertex of a double-napped cone, three special conics are created. • Circle • Ellipse • Parabola • Hyperbola • Intersecting Lines • Line • Point

CONIC SECTIONS Circles

Circles Definition A circle is a locus of points such that every point is equidistant from a fixed point, called the center. Locus – a set of points that follow a general rule

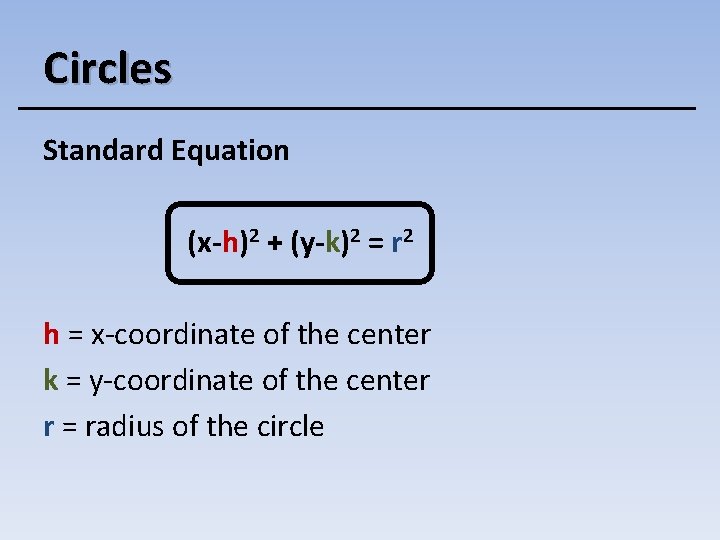
Circles Standard Equation (x-h)2 + (y-k)2 = r 2 h = x-coordinate of the center k = y-coordinate of the center r = radius of the circle

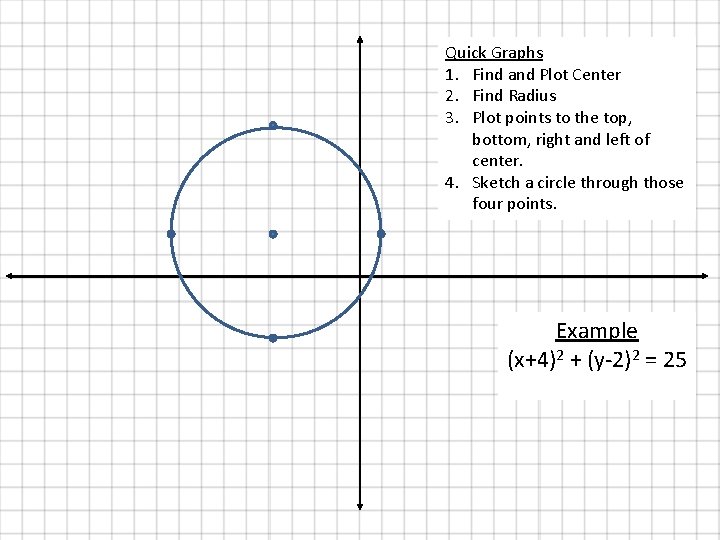
Quick Graphs 1. Find and Plot Center 2. Find Radius 3. Plot points to the top, bottom, right and left of center. 4. Sketch a circle through those four points. Example (x+4)2 + (y-2)2 = 25

Writing Equations 1. Know the standard form of the equation 2. Often it helps if you sketch the curve described 3. Find any critical values needed for the equation 4. Plug those into the equation

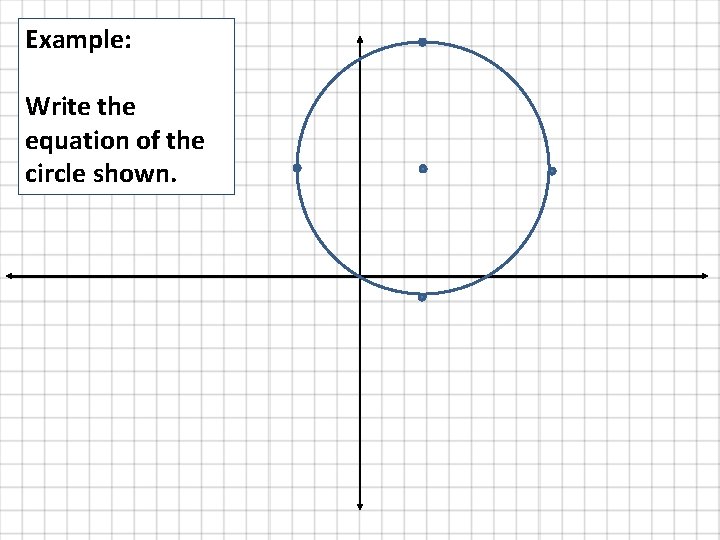
Example: Write the equation of the circle shown.

Examples • h = -3 k = 0 1. Find h, k, and r 2. Use the formula 3. Plug in h, k, and r 4. Simplify

Examples Write the equation of the circle with the following characteristics: Center (5, -4) passing through (8, 8) (x-5)2 + (y--4)2 = r 2 (8 -5)2 + (8+4)2 = r 2 (3)2 + 153 = (12)2 r 2 = r 2 1. Plug in h and k. 2. Plug in given x and y. 3. Solve for r-squared 4. Rewrite using h, k, and r-squared (x-5)2 + (y+4)2 = 153

Examples Write the equation of the circle with the following characteristics. Diameter running between (-2, 4) and (7, 9) 1. Find Midpoint/center 2. Plug in h and k. 3. Plug in either given x and y. 4. Solve for r-squared Rewrite using h, k, and r-squared

Assignment #1 – Conics and Circles