Congruent Triangles Demonstration This resource provides animated demonstrations

Congruent Triangles – Demonstration This resource provides animated demonstrations of the mathematical method. Check animations and delete slides not needed for your class.

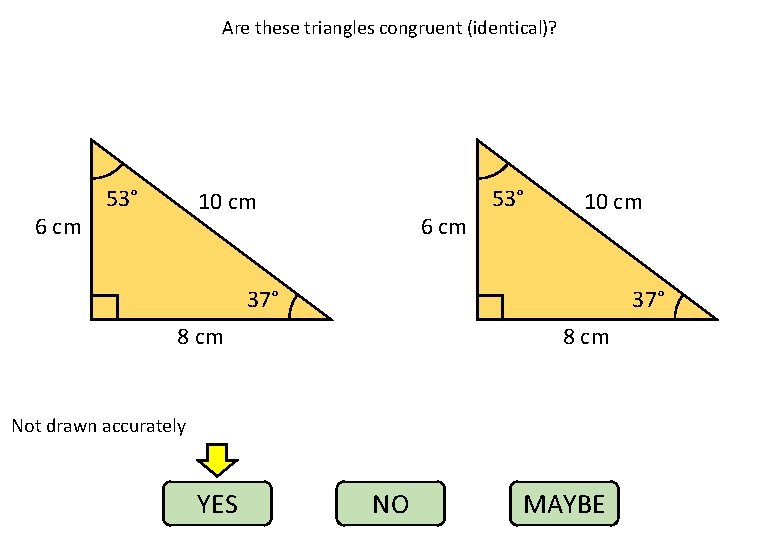
Are these triangles congruent (identical)? 6 cm 53° 10 cm 37° 8 cm Not drawn accurately YES NO MAYBE

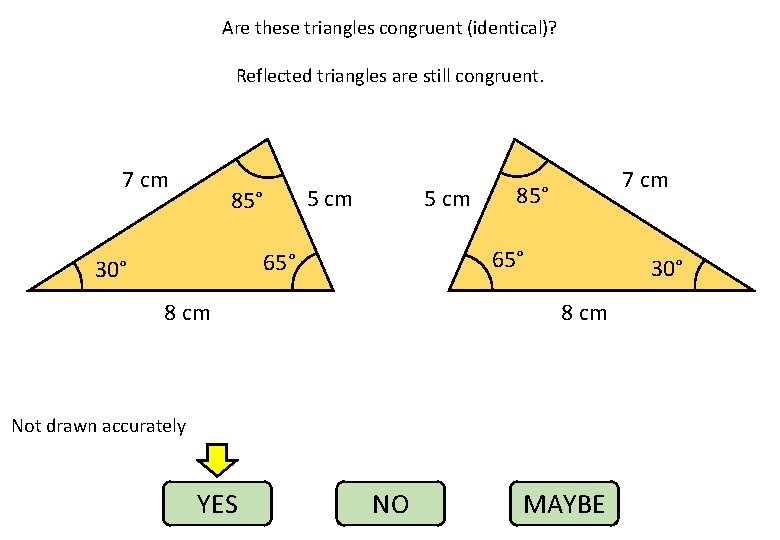
Are these triangles congruent (identical)? Reflected triangles are still congruent. 7 cm 85° 5 cm 85° 65° 30° 7 cm 8 cm 30° 8 cm Not drawn accurately YES NO MAYBE

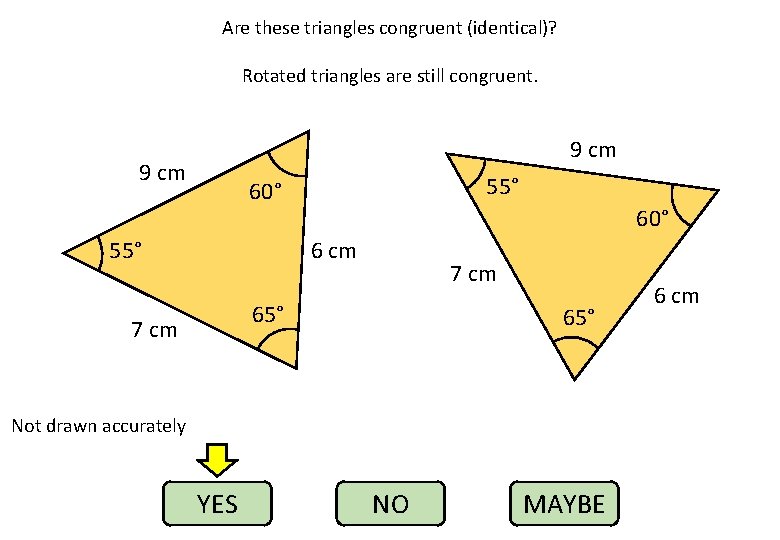
Are these triangles congruent (identical)? Rotated triangles are still congruent. 9 cm 55° 60° 6 cm 7 cm 65° Not drawn accurately YES NO MAYBE 6 cm

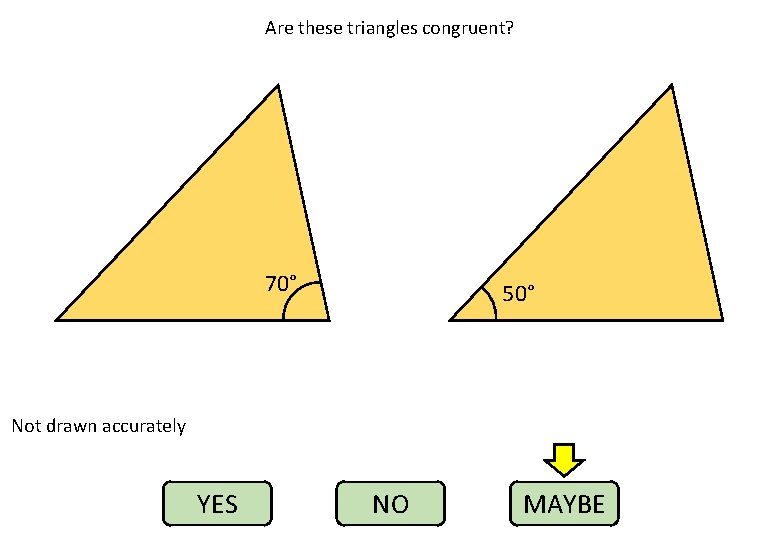
Are these triangles congruent? 70° 50° Not drawn accurately YES NO MAYBE

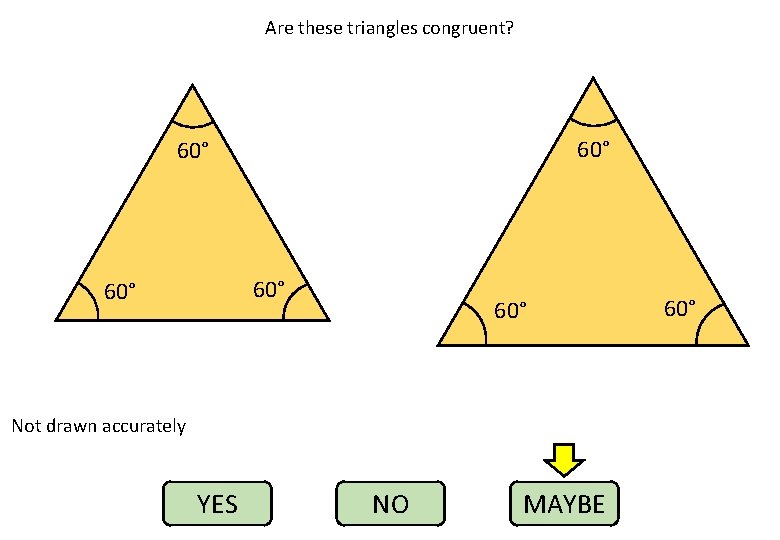
Are these triangles congruent? 60° 60° 60° Not drawn accurately YES NO MAYBE 60°

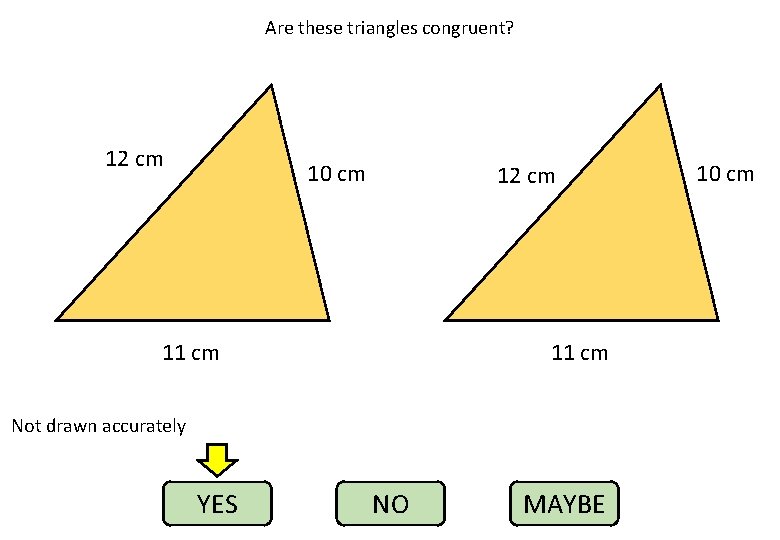
Are these triangles congruent? 12 cm 10 cm 12 cm 11 cm Not drawn accurately YES NO MAYBE 10 cm

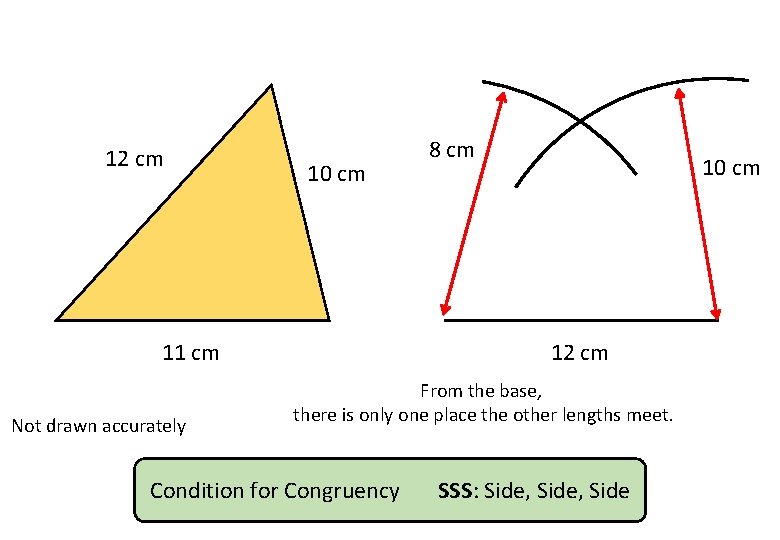
12 cm 10 cm 11 cm Not drawn accurately 8 cm 10 cm 12 cm From the base, there is only one place the other lengths meet. Condition for Congruency SSS: Side, Side

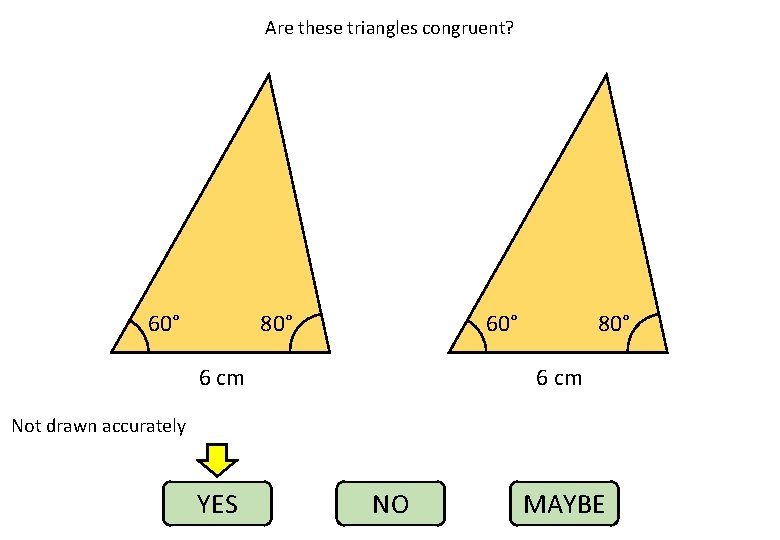
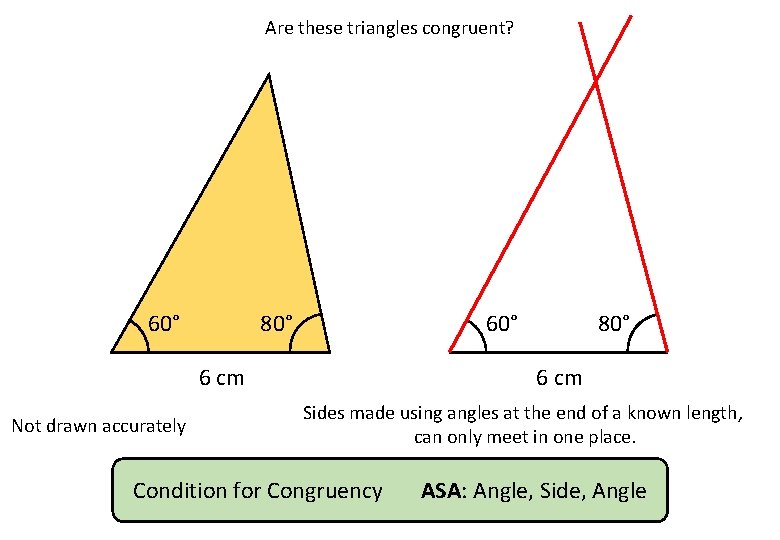
Are these triangles congruent? 60° 80° 6 cm Not drawn accurately YES NO MAYBE

Are these triangles congruent? 60° 80° 6 cm Not drawn accurately 80° 6 cm Sides made using angles at the end of a known length, can only meet in one place. Condition for Congruency ASA: Angle, Side, Angle

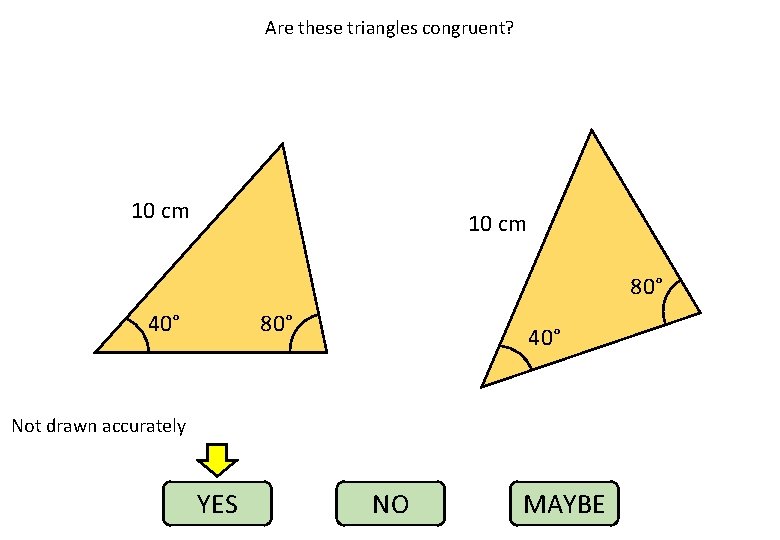
Are these triangles congruent? 10 cm 80° 40° Not drawn accurately YES NO MAYBE

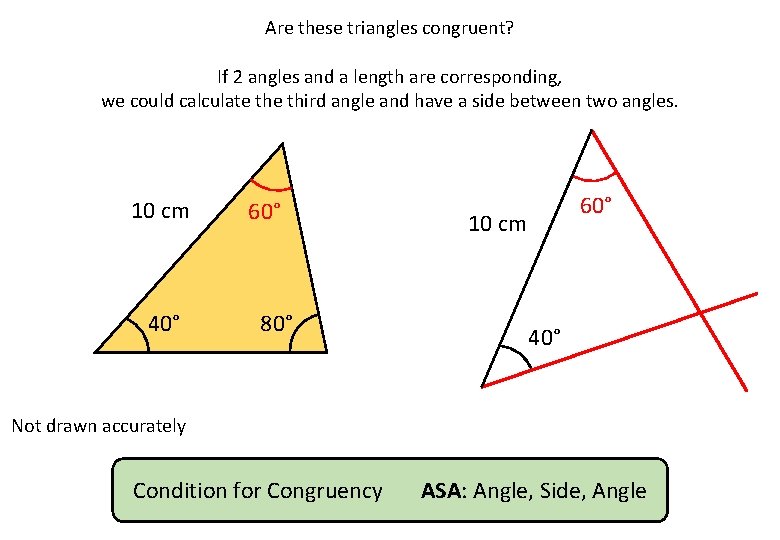
Are these triangles congruent? If 2 angles and a length are corresponding, we could calculate third angle and have a side between two angles. 10 cm 40° 60° 80° 60° 10 cm 40° Not drawn accurately Condition for Congruency ASA: Angle, Side, Angle

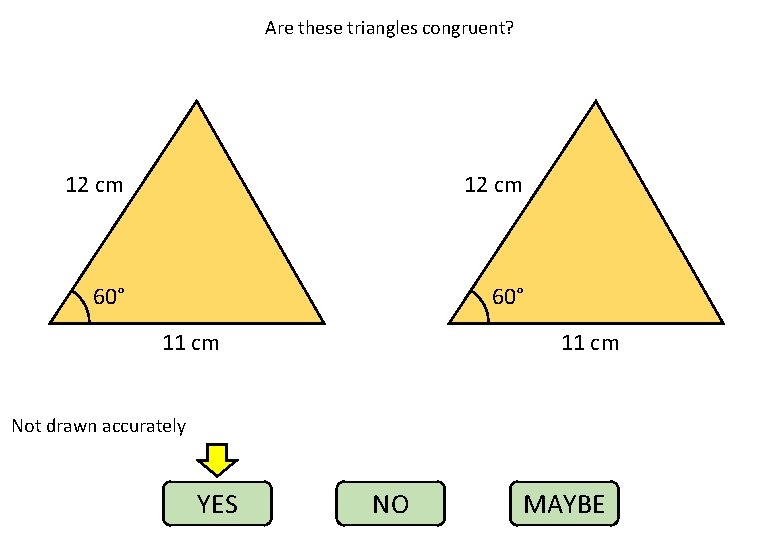
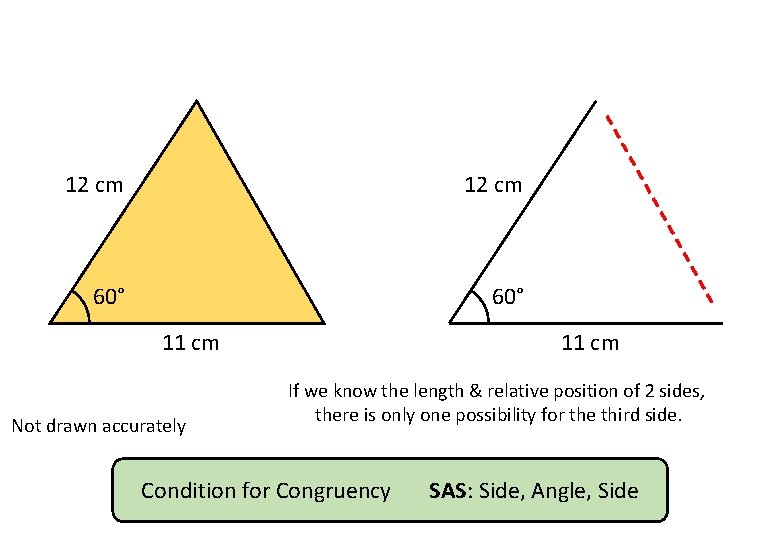
Are these triangles congruent? 12 cm 60° 11 cm Not drawn accurately YES NO MAYBE

12 cm 60° 11 cm Not drawn accurately 11 cm If we know the length & relative position of 2 sides, there is only one possibility for the third side. Condition for Congruency SAS: Side, Angle, Side

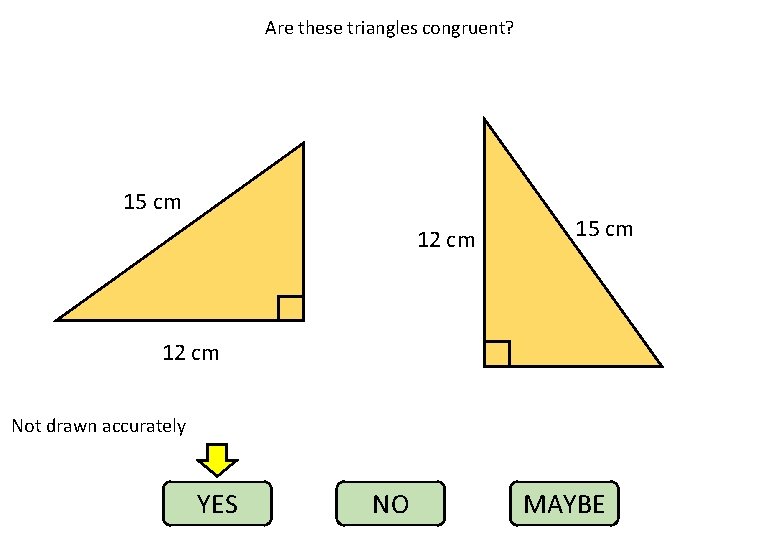
Are these triangles congruent? 15 cm 12 cm Not drawn accurately YES NO MAYBE

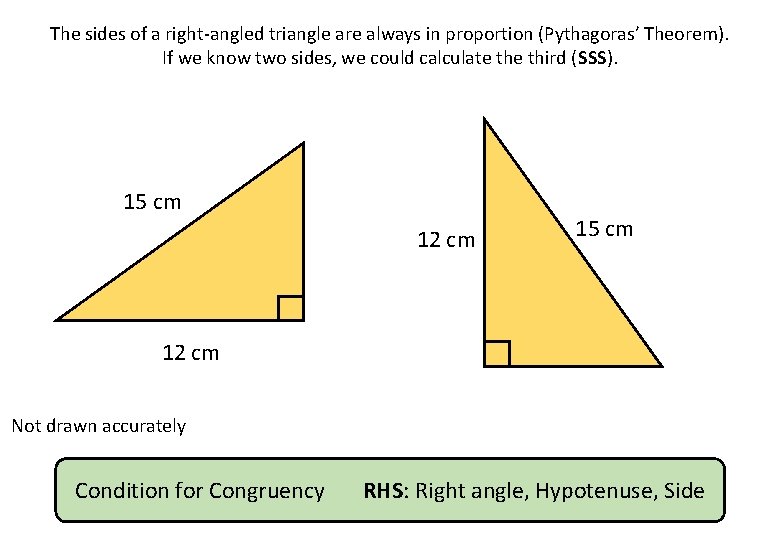
The sides of a right-angled triangle are always in proportion (Pythagoras’ Theorem). If we know two sides, we could calculate third (SSS). 15 cm 12 cm Not drawn accurately Condition for Congruency RHS: Right angle, Hypotenuse, Side

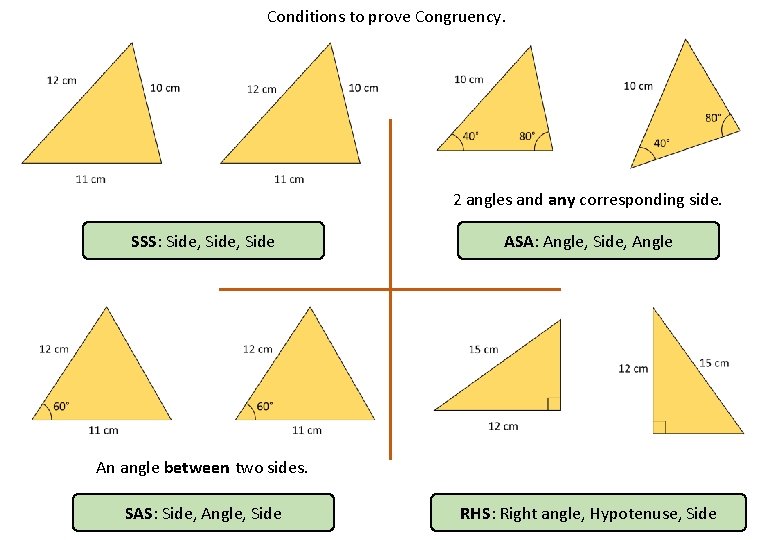
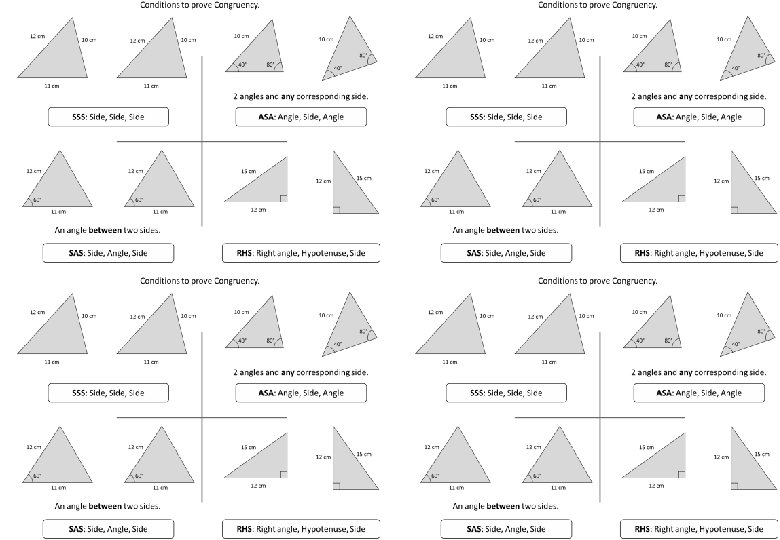
Conditions to prove Congruency. 2 angles and any corresponding side. SSS: Side, Side ASA: Angle, Side, Angle An angle between two sides. SAS: Side, Angle, Side RHS: Right angle, Hypotenuse, Side

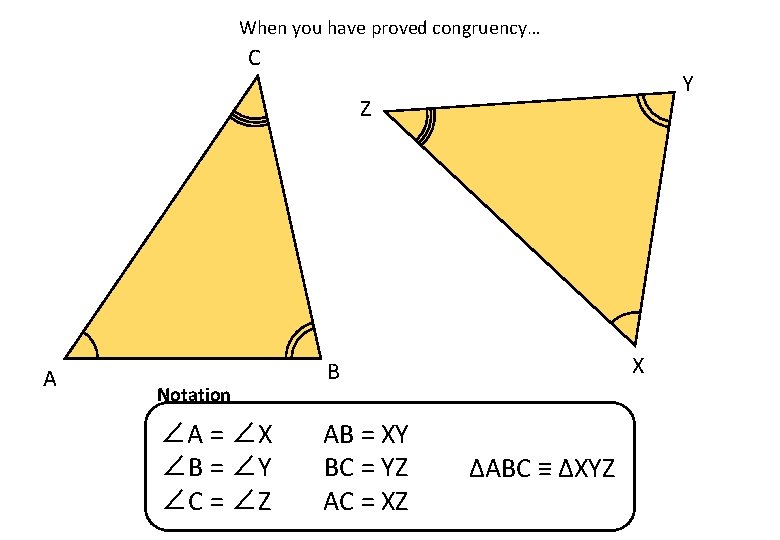
When you have proved congruency… C Y Z A Notation ∠A = ∠X ∠B = ∠Y ∠C = ∠Z X B AB = XY BC = YZ AC = XZ ∆ABC ≡ ∆XYZ

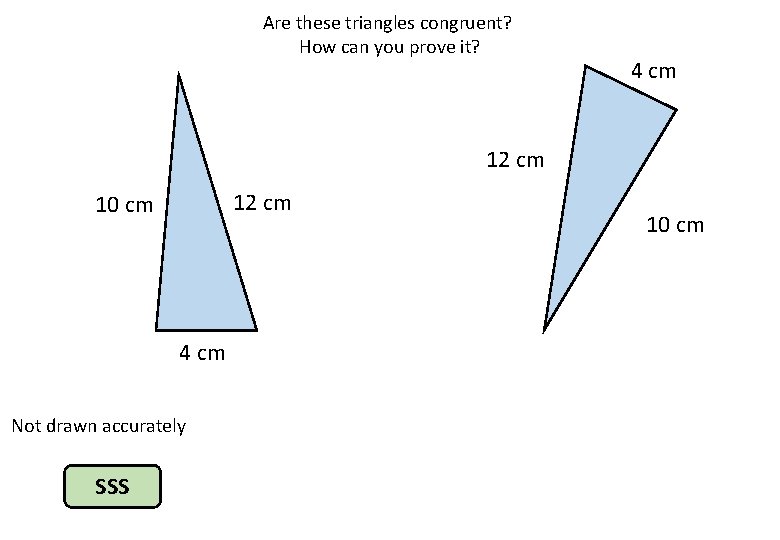
Are these triangles congruent? How can you prove it? 4 cm 12 cm 10 cm 4 cm Not drawn accurately SSS 10 cm

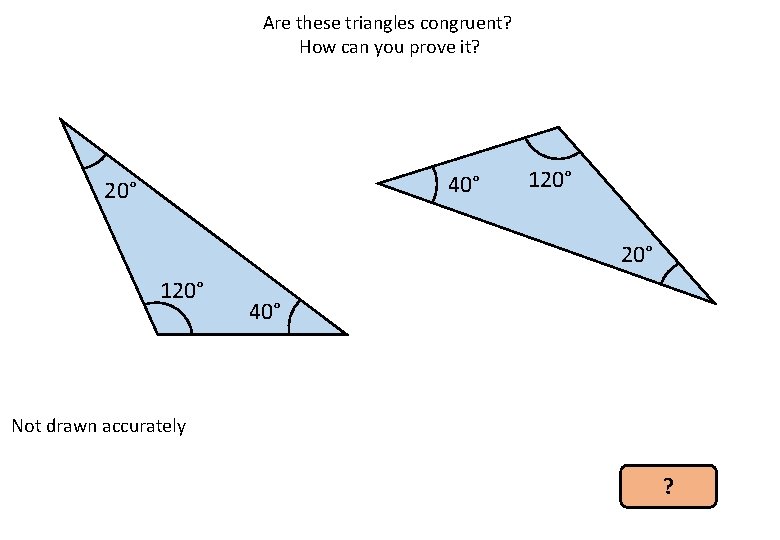
Are these triangles congruent? How can you prove it? 40° 20° 120° 40° Not drawn accurately ?

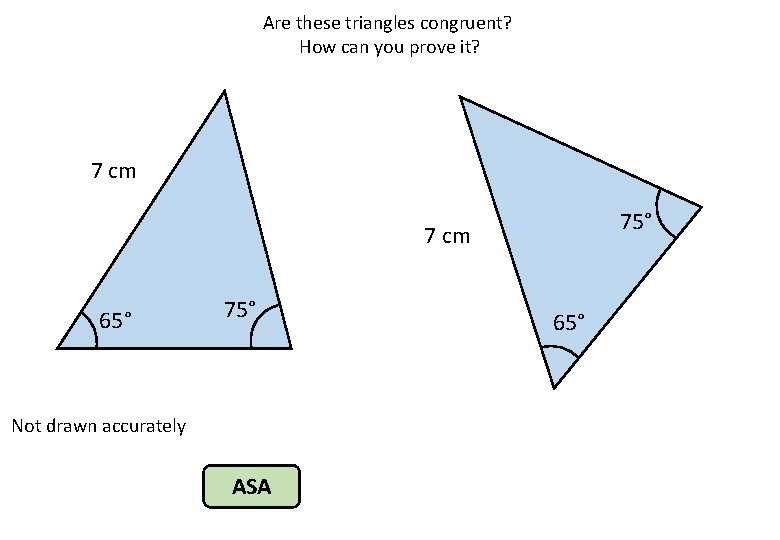
Are these triangles congruent? How can you prove it? 7 cm 75° 7 cm 65° 75° Not drawn accurately ASA 65°

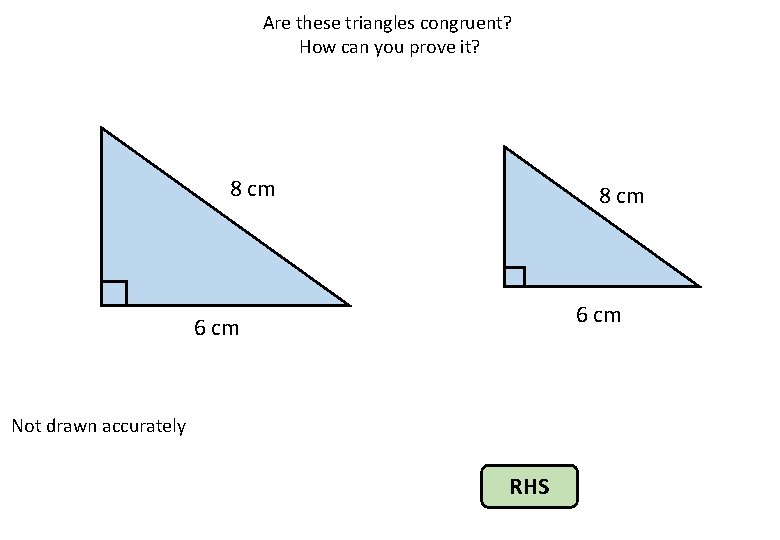
Are these triangles congruent? How can you prove it? 8 cm 6 cm Not drawn accurately RHS

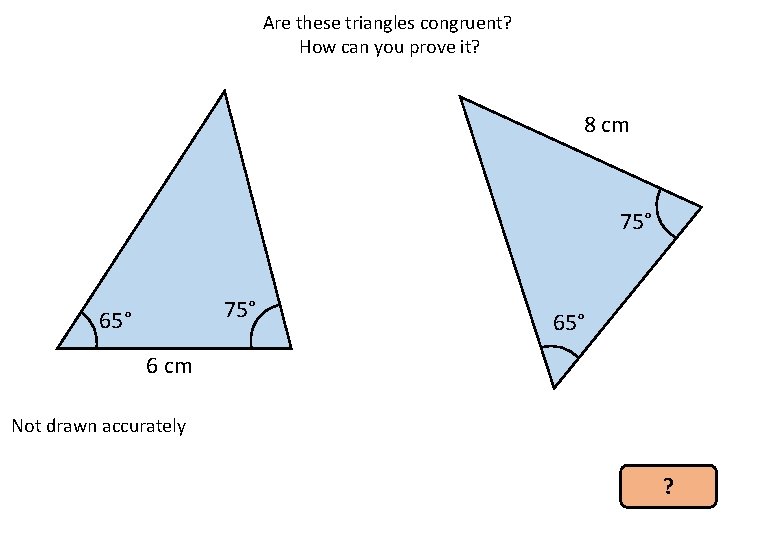
Are these triangles congruent? How can you prove it? 8 cm 75° 65° 6 cm Not drawn accurately ?

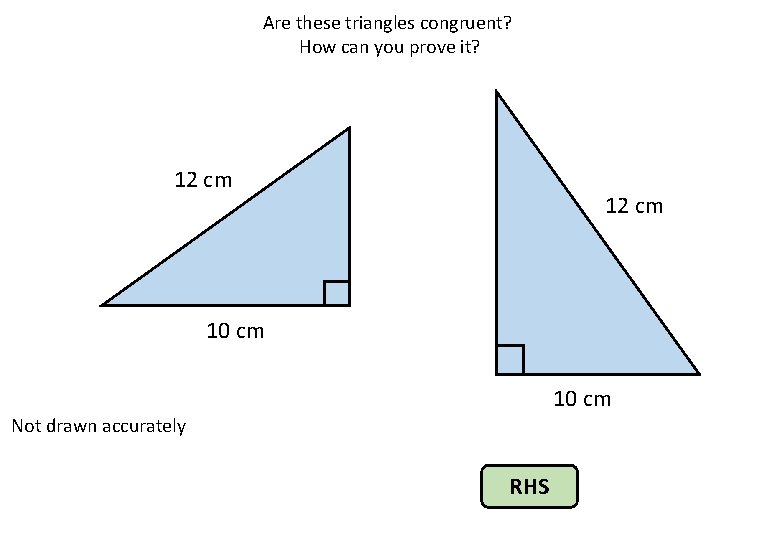
Are these triangles congruent? How can you prove it? 12 cm 10 cm Not drawn accurately RHS

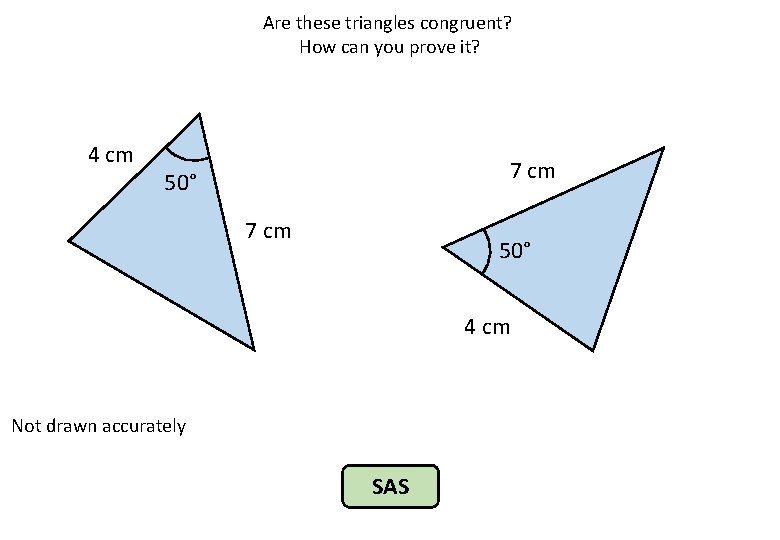
Are these triangles congruent? How can you prove it? 4 cm 7 cm 50° 4 cm Not drawn accurately SAS

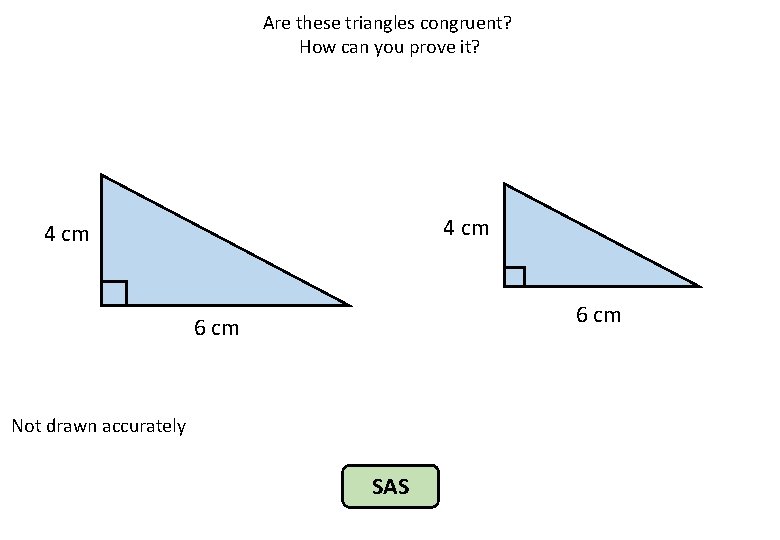
Are these triangles congruent? How can you prove it? 4 cm 6 cm Not drawn accurately SAS

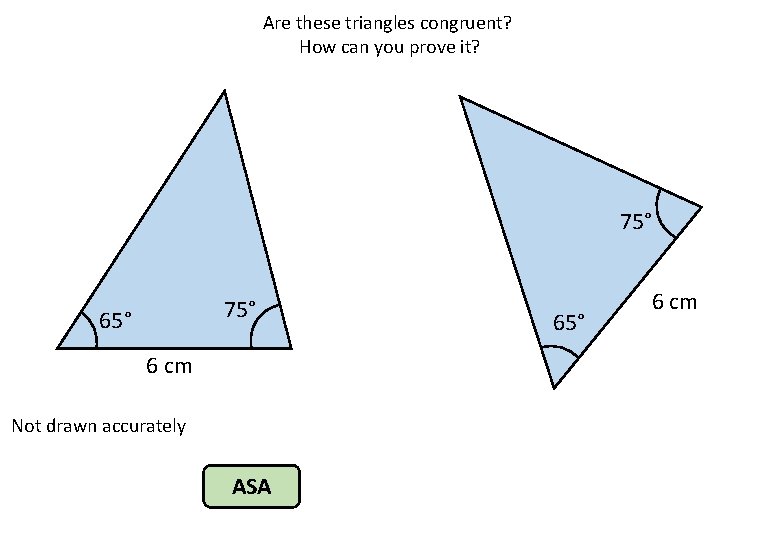
Are these triangles congruent? How can you prove it? 75° 65° 6 cm Not drawn accurately ASA 65° 6 cm

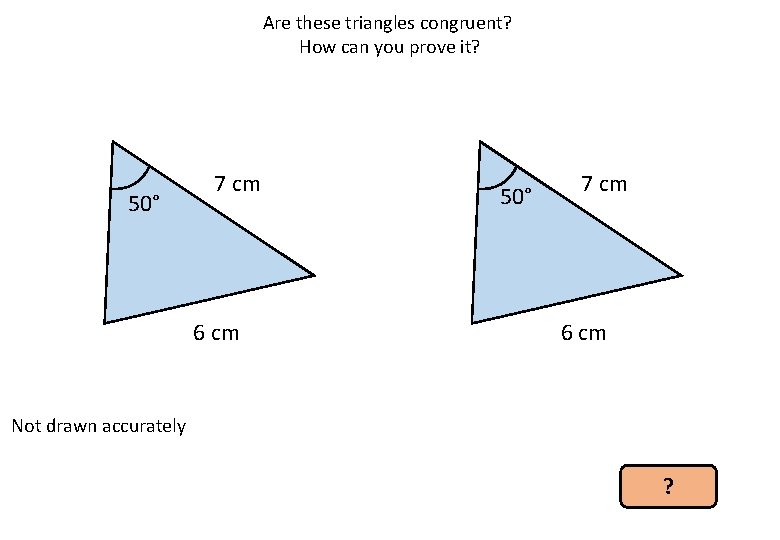
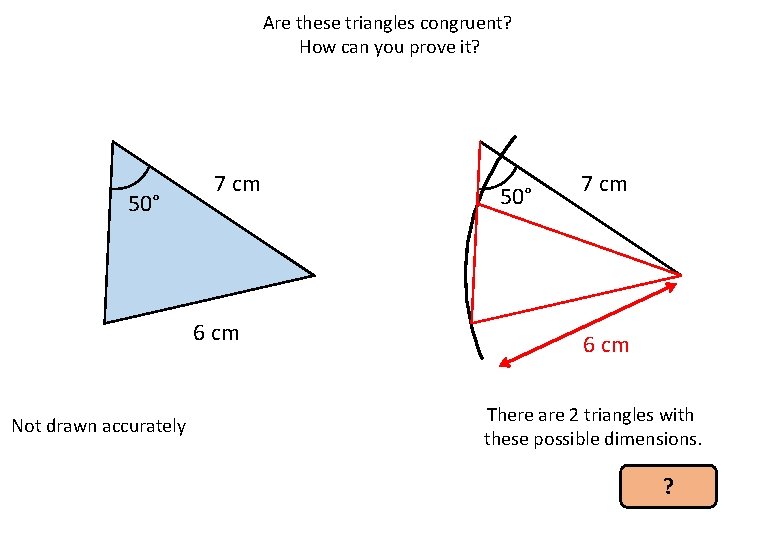
Are these triangles congruent? How can you prove it? 50° 7 cm 6 cm Not drawn accurately ?

Are these triangles congruent? How can you prove it? 50° 7 cm 6 cm Not drawn accurately 50° 7 cm 6 cm There are 2 triangles with these possible dimensions. ?

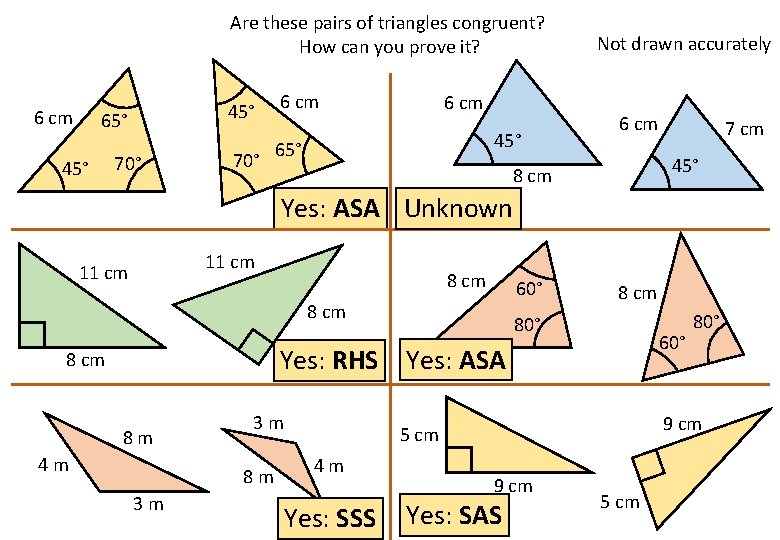
Are these pairs of triangles congruent? How can you prove it? 6 cm 45° 65° 45° 70° 6 cm 45° 65° Not drawn accurately 6 cm 7 cm 45° 8 cm Yes: ASA Unknown 11 cm 8 cm 60° 8 cm 80° 60° Yes: RHS Yes: ASA 8 cm 8 m 4 m 3 m 8 m 3 m 9 cm 5 cm 4 m Yes: SSS 80° 9 cm Yes: SAS 5 cm

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk