Congruent Triangles Chapter 4 Name Congruent figures have

• Congruent figures have the ____ shape and size. • Congruent ______have congruent

Naming Congruent Parts • ∆TJD ∆RCF List the congruent corresponding parts. • Sides: •

Naming Congruent Parts • ∆WYS ∆MKV. • Draw the two triangles in your notes

Finding Congruent Triangles Decide whether the triangles are congruent. Justify your answer. AC EC

Finding Congruent Triangles • Can you conclude JKL MNL? Justify your answer in the

Theorem 4 -1 • If two angles of one triangle are congruent to two

Proving Triangles Congruent Write your answer on the space provided • Given <A <D,

Summary: Answer in complete sentences. • Explain why it is important that PACH is

Side-Side (SSS) Postulate 4 -1 • If the three sides of one triangle are

Side-Angle-Side (SAS) Postulate 4 -2: • If two sides and the included angle of

Using SAS • RS TK, What other information do you need to prove RSK

Using SAS • What other information do you need to prove ABC CDA by

Are the Triangles Congruent? • From the given information, you can prove: RED Explain.

Are the Triangles Congruent? • From the given information, can you prove • AEB

Angle-Side Angle (ASA) Postulate If two angles and the included side of one triangle

Using ASA • A. Which triangle is congruent to CAT by the ASA Postulate?

Using ASA • Which triangle is congruent to CAT by the ASA Postulate? •

USING ASA • Can you conclude that INF is congruent to either of the

Real-World Connection • Lacrosse: Study what you are given and what you are to

Solution: • Proof: <ABC <AED because all right angles are congruent. You are given

Write a Proof • Given: NM NP, <M <P • Prove: NML NPO

Angle-Side (AAS) Theorem 4 -2 If two angles and a non-included side of one

Writing a Proof • Study what you are given and what you are to

• With SSS, SAS, ASA, and AAS you know how to use three

Real-World Connection • Given: <Q • Prove: R, <QPS <RSP SQ PR

Summary: Answer in complete sentences. Explain why CPCTC is useful.

Isosceles and Equilateral Triangles 4 -5

• Isosceles triangles are common in the real world. • The congruent sides

The Isosceles Triangle Theorem 4 -3 If two sides of a triangle are congruent,

Converse of Isosceles Triangle Theorem: Theorem 4 -4 • If two angles of a

Theorem 4 -5 • The bisector of the vertex angle of an isosceles triangle

Using the Isosceles Triangle Theorem • Can you deduce that RUV is isosceles? Explain.

Using Algebra Find the value of y. a. 17 b. 27 c. 54 d.

Corollary • A corollary is a statement that follow immediately from a theorem. Corollary

Corollary to Theorem 4 -4 • If a triangle is equiangular, then the triangle

Summary: Answer in complete sentences. • An exterior angle to the vertex of an

• In a right triangle, the side opposite the right angle is the

HL Theorem To use the HL Theorem, you must show that three conditions are

Summary: Answer in complete sentences. How are SAS and HL alike and how are

Using Corresponding Parts of Congruent Triangles 4 -7

• Some triangles relationships are difficult to see because the triangles overlap. •

Identifying Common Parts • Separate and redraw the triangles. • Identify the common angle.

Slides: 49

Download presentation

Congruent Triangles Chapter 4 Name: ______________

• Congruent figures have the ____ shape and size. • Congruent ______have congruent corresponding parts – matching sides and angles. • When you name congruent polygons always list _______ vertices in the same order.

Naming Congruent Parts • ∆TJD ∆RCF List the congruent corresponding parts. • Sides: • Angles: <T <R <J <C <D <F •

Naming Congruent Parts • ∆WYS ∆MKV. • Draw the two triangles in your notes • List the congruent corresponding parts. • Use three letters to name each angle.

Finding Congruent Triangles Decide whether the triangles are congruent. Justify your answer. AC EC ____ AB ED BC DC <A < E < B <<D <BCA <DCE AB = 3 = ED BC = 4 = DC ____ All right<‘s ____ <‘s ABC EDC by the definition of congruent triangles.

Finding Congruent Triangles • Can you conclude JKL MNL? Justify your answer in the space below:

Theorem 4 -1 • If two angles of one triangle are congruent to two angles of another triangle, then the third angles are congruent. <C <F

Proving Triangles Congruent

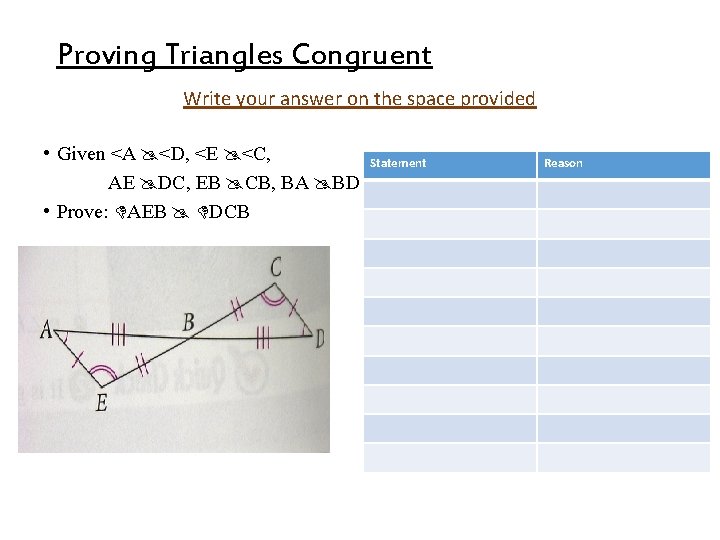
Proving Triangles Congruent Write your answer on the space provided • Given <A <D, <E <C, AE DC, EB CB, BA BD • Prove: AEB DCB Statement Reason

Summary: Answer in complete sentences. • Explain why it is important that PACH is congruent to OLDE.

Triangle Congruence by SSS and SAS 4 -2

Side-Side (SSS) Postulate 4 -1 • If the three sides of one triangle are congruent to the three sides of another triangle, then the two triangles are congruent. GHF PQR

Side-Angle-Side (SAS) Postulate 4 -2: • If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent. BCA FDE

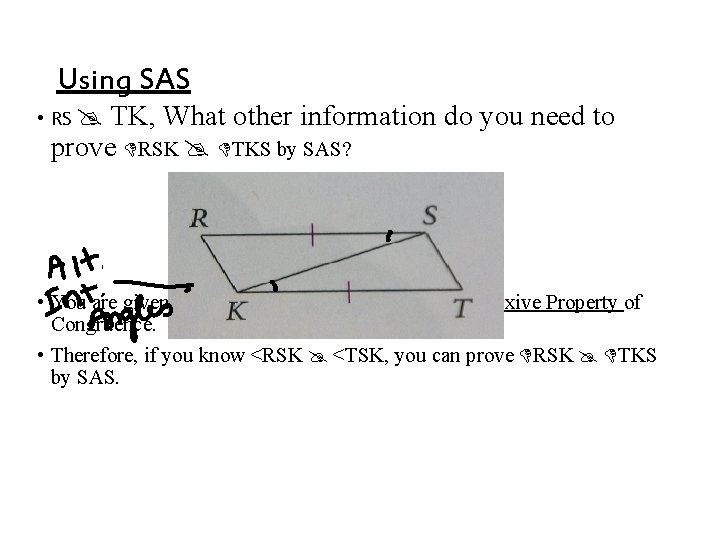
Using SAS • RS TK, What other information do you need to prove RSK TKS by SAS? • You are given RS TK. Also KS by the Reflexive Property of Congruence. • Therefore, if you know <RSK <TSK, you can prove RSK TKS by SAS.

Using SAS • What other information do you need to prove ABC CDA by SAS?

Are the Triangles Congruent? • From the given information, you can prove: RED Explain. • Given: RE CA, RD CT, < R <T CAT?

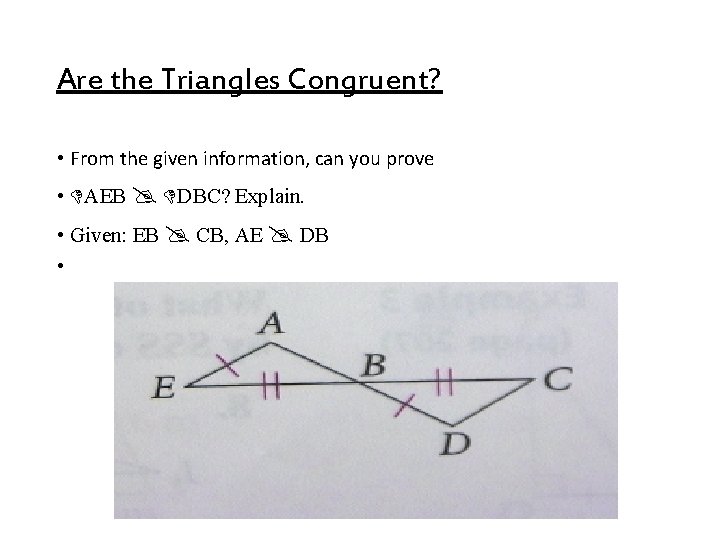
Are the Triangles Congruent? • From the given information, can you prove • AEB DBC? Explain. • Given: EB CB, AE DB •

Triangle Congruence by ASA and AAS 4 -3

Angle-Side Angle (ASA) Postulate If two angles and the included side of one triangle are congruent to two angles the included side of another triangle, then the two triangles are congruent. • HGB NKP

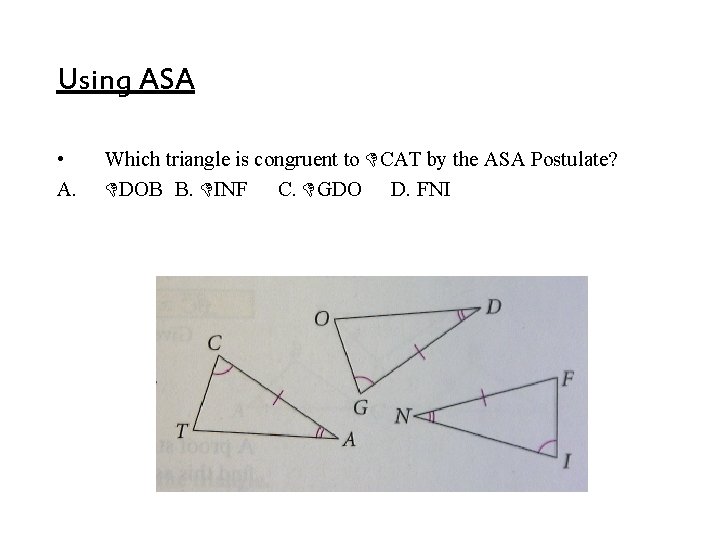
Using ASA • A. Which triangle is congruent to CAT by the ASA Postulate? DOB B. INF C. GDO D. FNI

Using ASA • Which triangle is congruent to CAT by the ASA Postulate? • <C <G, CA GD, and <A <D • CAT GDO by ASA, Choice C is correct.

USING ASA • Can you conclude that INF is congruent to either of the other two triangles? Explain.

Real-World Connection • Lacrosse: Study what you are given and what you are to prove about the lacrosse goal. Then write a proof that uses ASA. • Given: <CAB angles. <DAE, AB AE, <ABC and <AED are right • Prove: ABC AED

Solution: • Proof: <ABC <AED because all right angles are congruent. You are given that AB AE and <CAB <DAE. Therefore, ABC AED by ASA

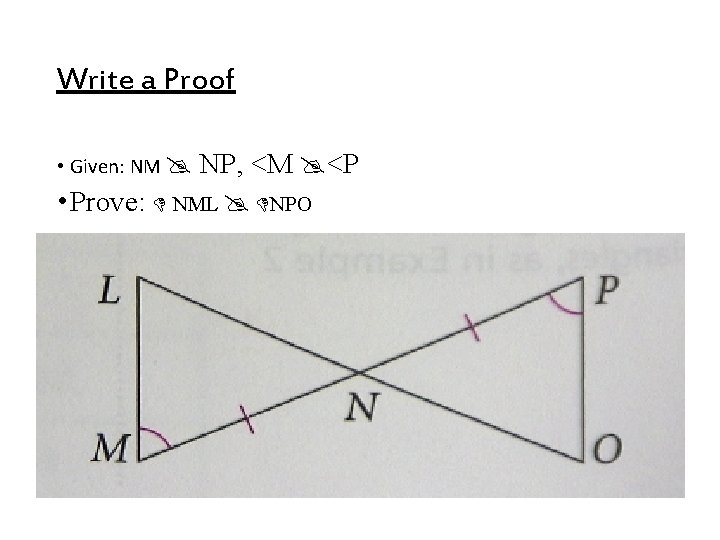
Write a Proof • Given: NM NP, <M <P • Prove: NML NPO

Angle-Side (AAS) Theorem 4 -2 If two angles and a non-included side of one triangle are congruent to two angles and the corresponding nonincluded side of another triangle, then the triangles are congruent. CDM XGT

Writing a Proof • Study what you are given and what you are to prove. Then plan a proof that uses AAS. • Given XQ TR, XR bisects QT. • Prove: XMQ RMT • Hint: XQ TR gives two pairs of congruent alternate interior angles. XR bisects QT means QM TM. Use AAS.

Using Congruent Triangles: CPCTC 4 -4

• With SSS, SAS, ASA, and AAS you know how to use three parts of triangles to show that the triangles are congruent. • Once you have triangles congruent, you can make conclusions about their other parts because, by definition, corresponding parts of congruent triangles are congruent. • You can abbreviate this as CPCTC.

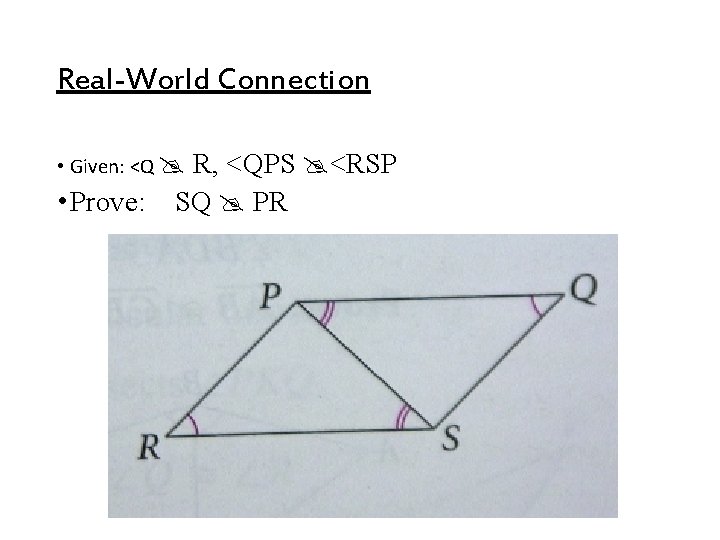
Real-World Connection • Given: <Q • Prove: R, <QPS <RSP SQ PR

Summary: Answer in complete sentences. Explain why CPCTC is useful.

Isosceles and Equilateral Triangles 4 -5

• Isosceles triangles are common in the real world. • The congruent sides of an isosceles triangle are called legs. The two congruent sides form the vertex angle. • The third side is called the base. The other two angles are the base angles.

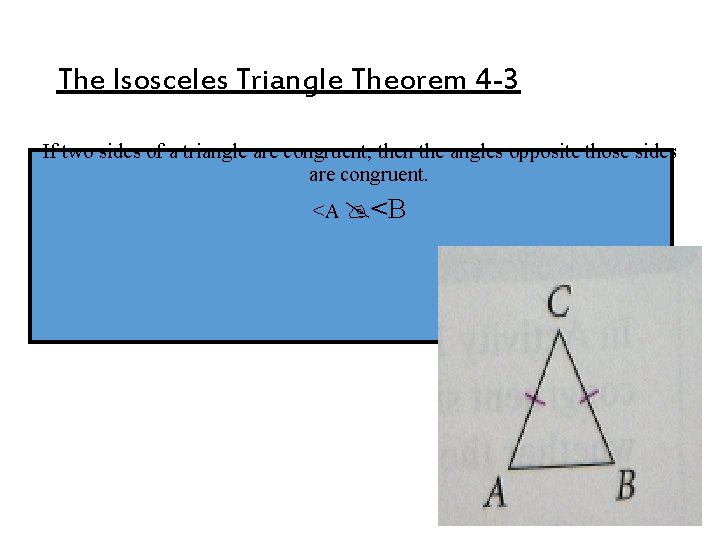
The Isosceles Triangle Theorem 4 -3 If two sides of a triangle are congruent, then the angles opposite those sides are congruent. <A <B

Converse of Isosceles Triangle Theorem: Theorem 4 -4 • If two angles of a triangle are congruent, then the sides opposite the angles are congruent. • AC BC

Theorem 4 -5 • The bisector of the vertex angle of an isosceles triangle is the perpendicular bisector of the base. • CD AB and CD bisects AB.

Using the Isosceles Triangle Theorem • Can you deduce that RUV is isosceles? Explain.

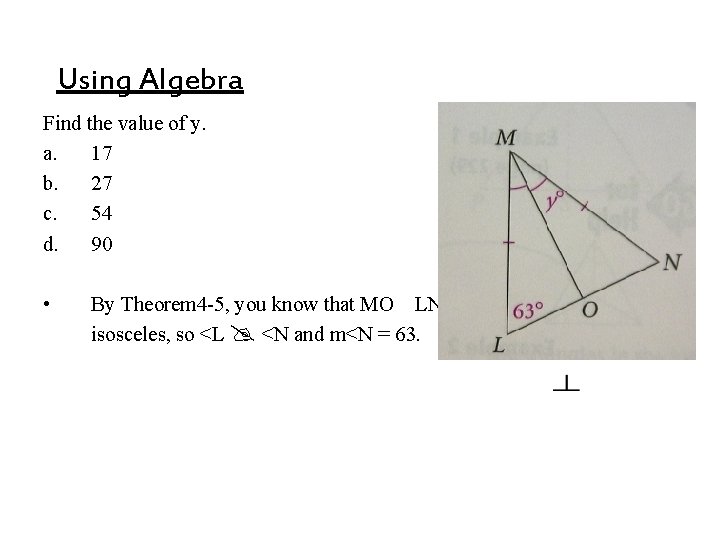
Using Algebra Find the value of y. a. 17 b. 27 c. 54 d. 90 • By Theorem 4 -5, you know that MO LN so <MON= 90, MLN is isosceles, so <L <N and m<N = 63.

Corollary • A corollary is a statement that follow immediately from a theorem. Corollary to Theorem 4 -3 • If a triangle is equilateral, then the triangle I equiangular. <X <Y <Z

Corollary to Theorem 4 -4 • If a triangle is equiangular, then the triangle is equilateral. XY YZ ZX

Summary: Answer in complete sentences. • An exterior angle to the vertex of an isosceles triangle measures 80. Find the angle measures of the triangle.

Congruence in Right Triangles 4 -6

• In a right triangle, the side opposite the right angle is the longest side and is called the hypotenuse. The other two sides are called the legs. Hypotenuse-Leg (HL) Theorem 4 -6 If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent.

HL Theorem To use the HL Theorem, you must show that three conditions are met. 1. There are two right triangles. 2. The triangles have congruent hypotenuses. 3. There is one pair of congruent legs.

Summary: Answer in complete sentences. How are SAS and HL alike and how are they different?

Using Corresponding Parts of Congruent Triangles 4 -7

• Some triangles relationships are difficult to see because the triangles overlap. • Overlapping triangles may have a common side or angle. • You can separate the overlapping triangles by redrawing them.

Identifying Common Parts • Separate and redraw the triangles. • Identify the common angle. • See example 1 on page 224