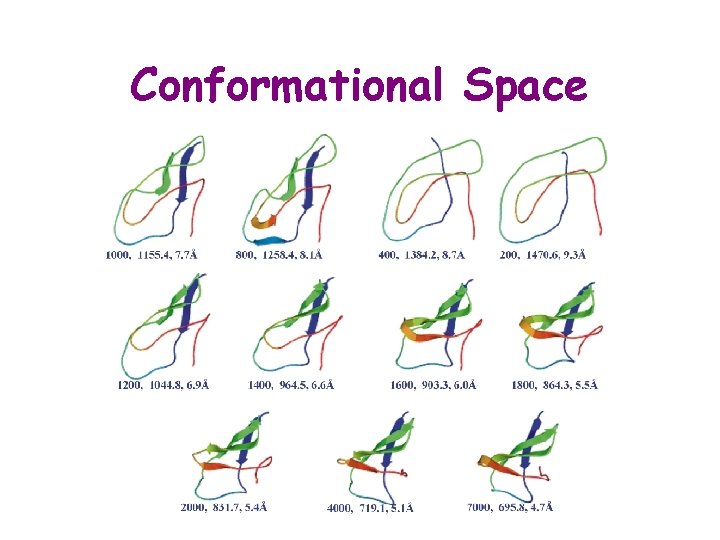
Conformational Space Conformational Space Conformation of a molecule

Conformational Space

Conformational Space § Conformation of a molecule: specification of the relative positions of all atoms in 3 D-space, § Typical parameterizations: § List of coordinates of atom centers § List of torsional angles (e. g. , the f-y-c for a protein) § Conformational space: Space of all conformations

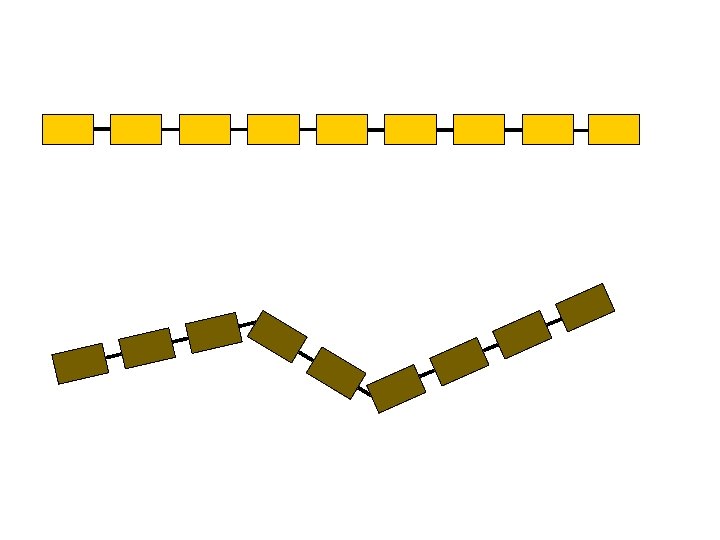
Conformational Space qj qi q. N-1 q 2 q. N q 1

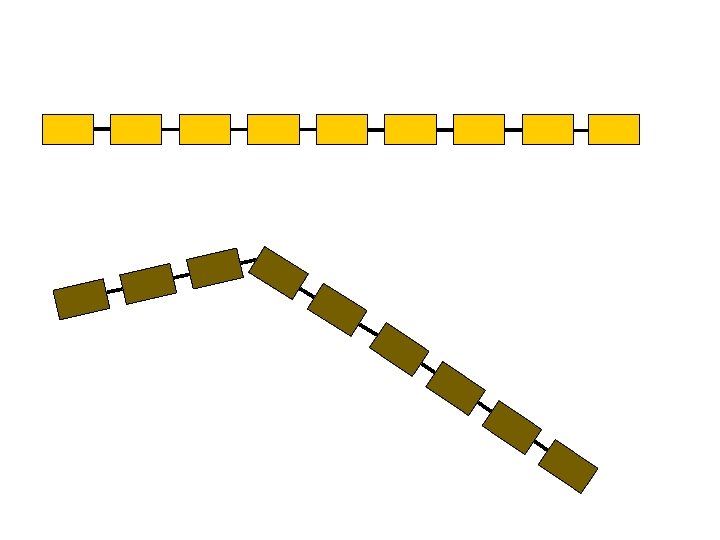
Conformational Space q 0 q 1 qn q 4 q 3

Relation to Robotics/Graphics q 0 q 1 q 2 qn t(t) q 4 Configuration space q 3

Need for a Metric § Simulation and sampling techniques can produce millions of conformations § Which conformations are similar? § Which ones are close to the folded one? § Do some conformations form small clusters (e. g. key intermediates while folding)?

Metric in Conformational Space § A metric over conformational space C is a function: d: c, c’ C d(c, c’) + {0} such that: § d(c, c’) = 0 c = c’ § d(c, c’) = d(c’, c) § d(c, c’) + d(c’, c”) d(c, c”) (non-degeneracy) (symmetry) (triangle inequality)

But not all metrics are “good” § Euclidean metric: d(c, c’) = Si=1, . . . , n(|fi-fi’|2+ |yi-yi’|2)

Metric in Conformational Space § A “good” metric should measure how well the atoms in two conformations can be aligned § Usual metrics: c. RMSD, d. RMSD

RMSD § Given two sets of n points in 3 A = {a 1, …, an} and B = {b 1, …, bn} § The RMSD between A and B is: RMSD(A, B) = [(1/n)Si=1, …, n||ai-bi||2]1/2 where ||ai-bi|| denotes the Euclidean distance between ai and bi in 3 § RMSD(A, B) = 0 iff ai = bi for all i

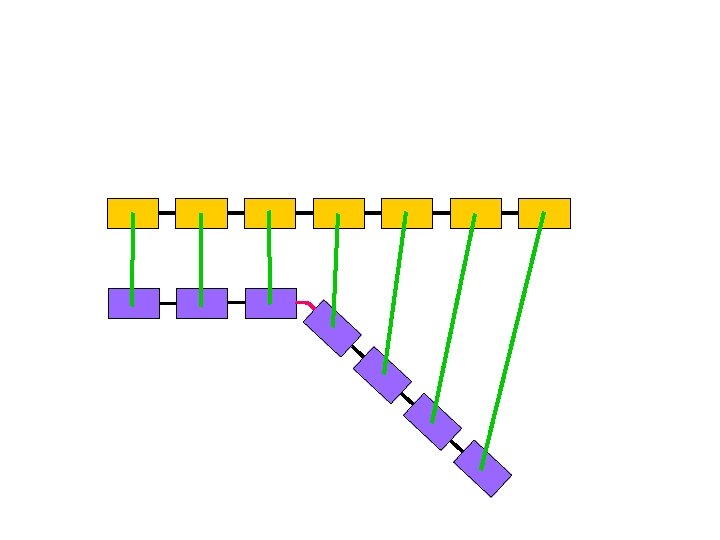
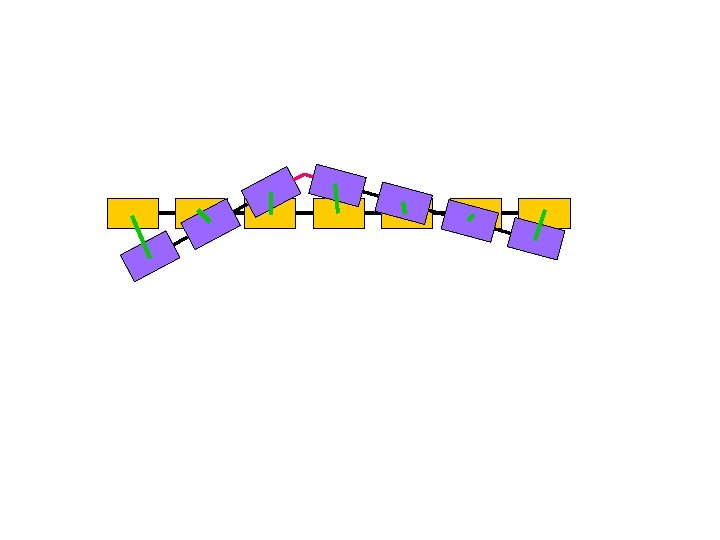
c. RMSD § Molecule M with n atoms a 1, …, an § Two conformations c and c’ of M § ai(c) is position of ai when M is at c § c. RMSD(c, c’) is the minimized RMSD between the two sets of atom centers: min. T[(1/n)Si=1, …, n||ai(c) – T(ai(c’))||2]1/2 where the minimization is over all possible rigid-body transform T

c. RMSD § c. RMSD verifies triangle inequality § c. RMSD takes linear time to compute § Often, c. RMSD is restricted to a subset of atoms, e. g. , the Ca atoms on a protein’s backbone

Representation Restricted to Ca Atoms Protein 1 tph - The positions of AA residue centers (Cα atoms) mainly determine the structure of a protein. - In structural comparison, people usually work only on the backbone of Cα atoms, and neglect the other atoms.

Possible project: Design a method for efficiently finding nearest neighbors in a sampled conformation space of a protein, using the c. RMSD metric.

d. RMSD § Molecule M with n atoms a 1, …, an § Two conformations c and c’ of M § {dij(c)}: n n symmetrical intra-molecular distance matrix in M at c § d. RMD(c, c’) is : [(1/n(n-1))Si=1, …, n-1 Sj=i+1, …, n(dij(c) – dij(c’))2]1/2 § {dij} is usually restricted to a subset of atoms, e. g. , the Ca atoms on a protein’s backbone

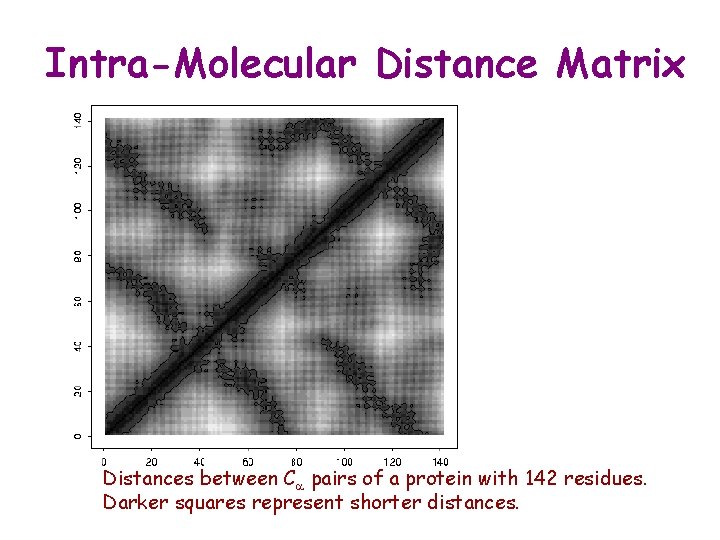
Intra-Molecular Distance Matrix Distances between Ca pairs of a protein with 142 residues. Darker squares represent shorter distances.

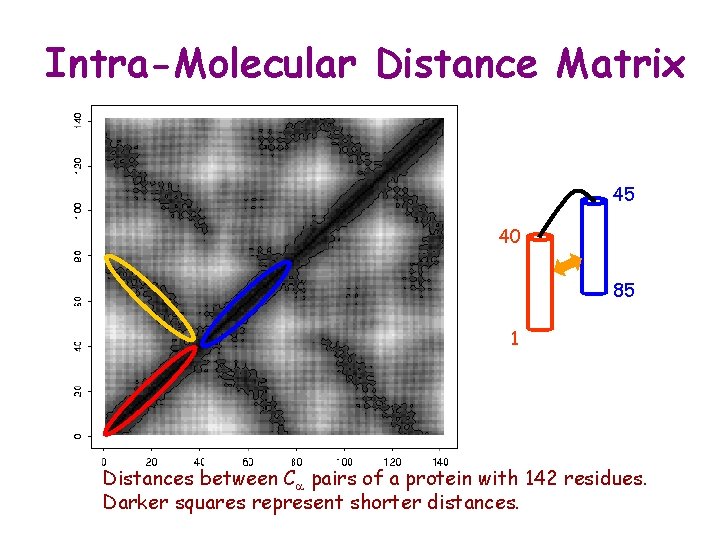
Intra-Molecular Distance Matrix 45 40 85 1 Distances between Ca pairs of a protein with 142 residues. Darker squares represent shorter distances.

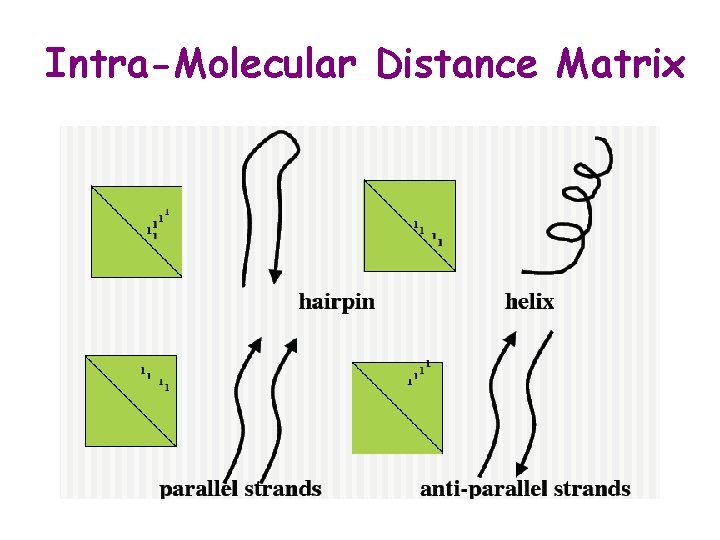
Intra-Molecular Distance Matrix

d. RMSD § Molecule M with n atoms a 1, …, an § Two conformations c and c’ of M § {dij(c)}: n n symmetrical intra-molecular distance matrix in M at c § d. RMSD(c, c’) = [(2/n(n-1))Si=1, …, n-1 Sj=i+1, …, n(dij(c) – dij(c’))2]1/2 § {dij} is usually restricted to a subset of atoms, e. g. , the Ca atoms on a protein’s backbone

d. RMSD § Molecule M with n atoms a 1, …, an § Two conformations c and c’ of M § {dij(c)}: n n symmetrical intra-molecular distance matrix in M at c § d. RMSD(c, c’) = [(2/n(n-1))Si=1, …, n-1 Sj=i+1, …, n(dij(c) – dij(c’))2]1/2 § {dij} is usually restricted to a subset of atoms, e. g. , the Ca atoms on a protein’s backbone § Advantage: No aligning transform § Drawback: Takes quadratic time to compute

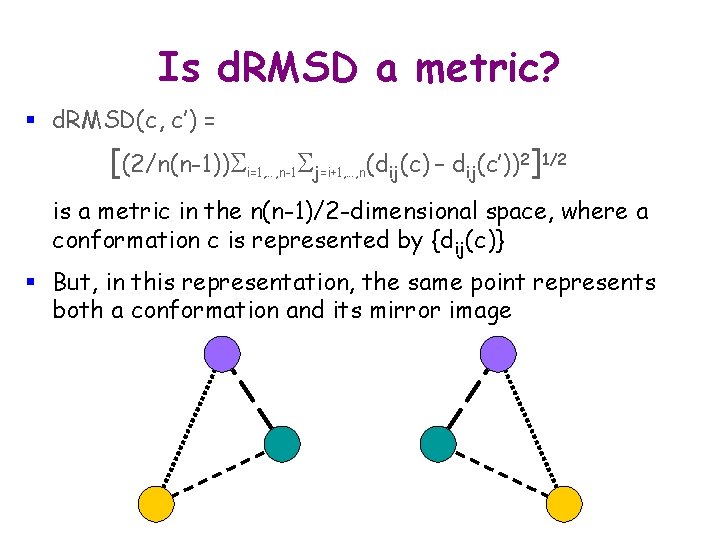
Is d. RMSD a metric? § d. RMSD(c, c’) = [(2/n(n-1))Si=1, …, n-1 Sj=i+1, …, n(dij(c) – dij(c’))2]1/2 is a metric in the n(n-1)/2 -dimensional space, where a conformation c is represented by {dij(c)} § But, in this representation, the same point represents both a conformation and its mirror image

k-Nearest-Neighbors Problem Given a set S of conformations of a protein and a query conformation c, find the k conformations in S most similar to c (w. r. t. c. RMSD, d. RMSD, other metric) Can be done in time O(N(log k + L)) where: - N = size of S - L = time to compare two conformations

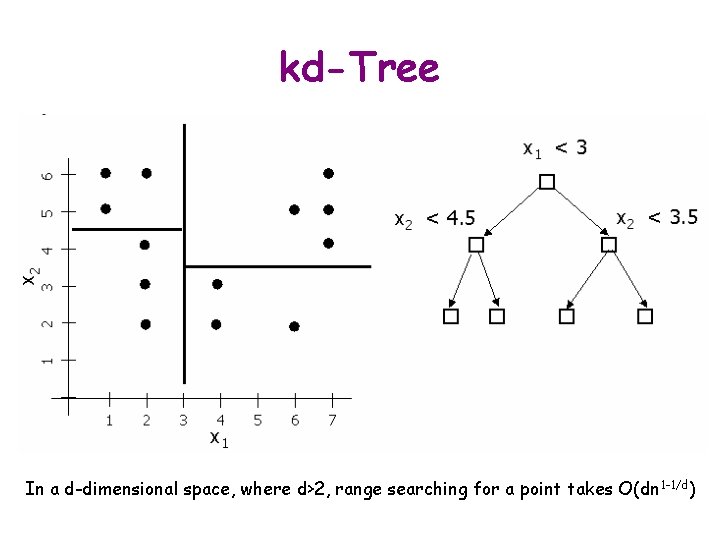
k-Nearest-Neighbors Problem The total time needed to compute the k nearest neighbors of every conformation in S is O(N 2(log k + L)) Much too long for large datasets where N ranges from 10, 000’s to millions!!! Can be improved by: 1. Reducing L 2. More efficient algorithm (e. g. , kd-tree)

kd-Tree In a d-dimensional space, where d>2, range searching for a point takes O(dn 1 -1/d)

k-Nearest-Neighbors Problem Idea: simplify protein’s description

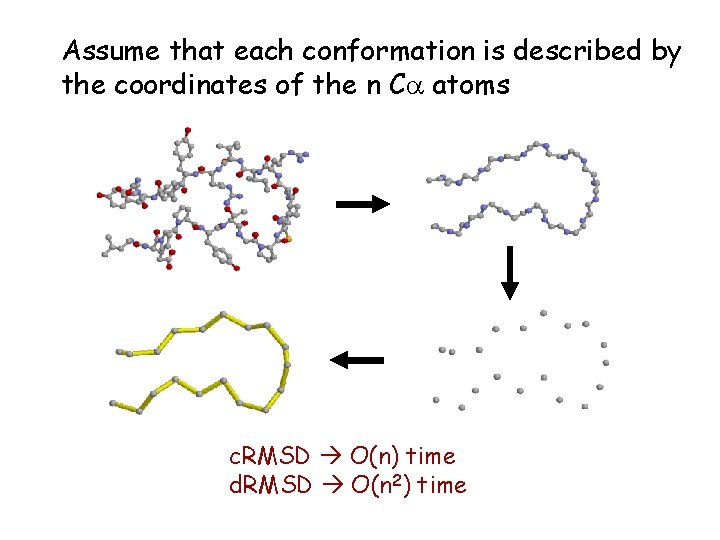
Assume that each conformation is described by the coordinates of the n Ca atoms c. RMSD O(n) time d. RMSD O(n 2) time

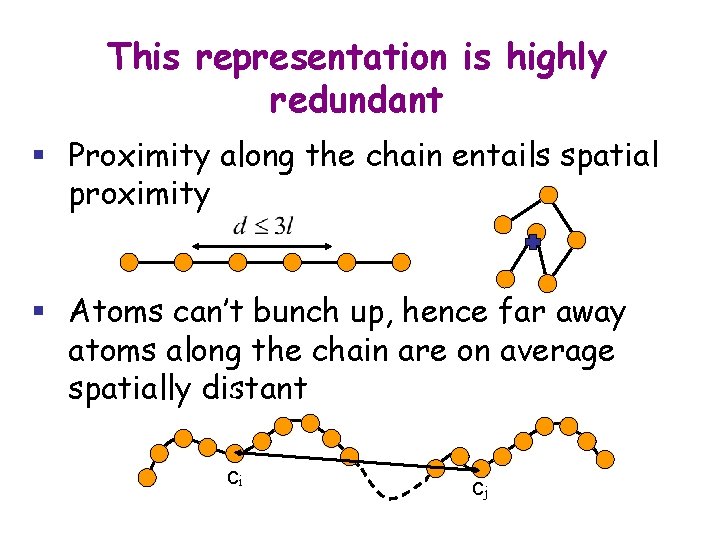
This representation is highly redundant § Proximity along the chain entails spatial proximity § Atoms can’t bunch up, hence far away atoms along the chain are on average spatially distant ci cj

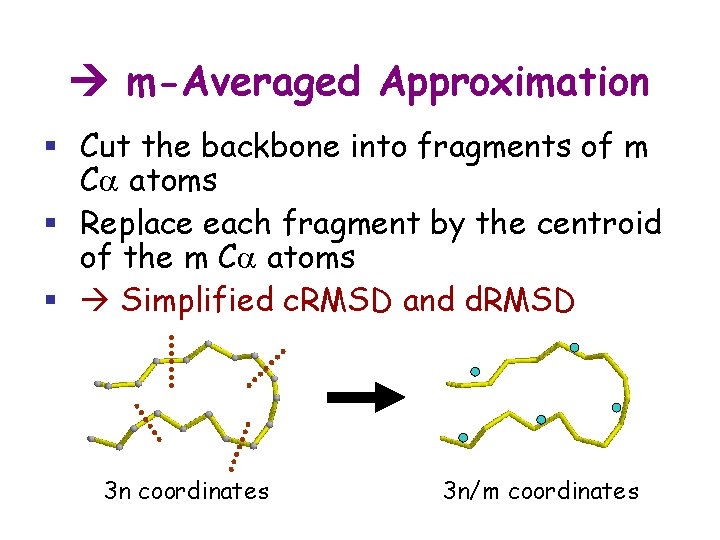
m-Averaged Approximation § Cut the backbone into fragments of m Ca atoms § Replace each fragment by the centroid of the m Ca atoms § Simplified c. RMSD and d. RMSD 3 n coordinates 3 n/m coordinates

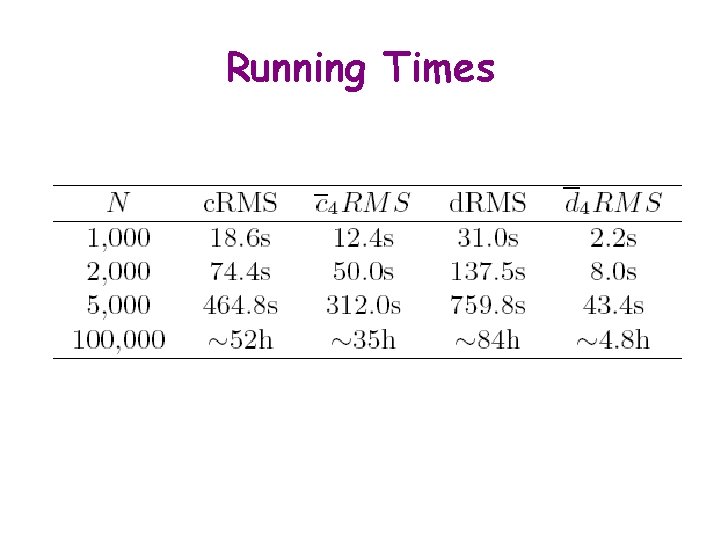
Evaluation: Test Sets [Lotan and Schwarzer, 2003] § 8 diverse proteins (54 -76 residues) § Decoy sets of N =10, 000 conformations from the Park-Levitt set [Park et al, 1997] Correlation: m c. RMSD d. RMSD 3 0. 99 0. 96 -0. 98 4 0. 98 -0. 99 0. 94 -0. 97 6 0. 92 -0. 99 0. 78 -0. 93 9 0. 81 -0. 98 0. 65 -0. 96 12 0. 54 -0. 92 0. 52 -0. 69 Higher correlation for random sets ( greater savings)

Running Times

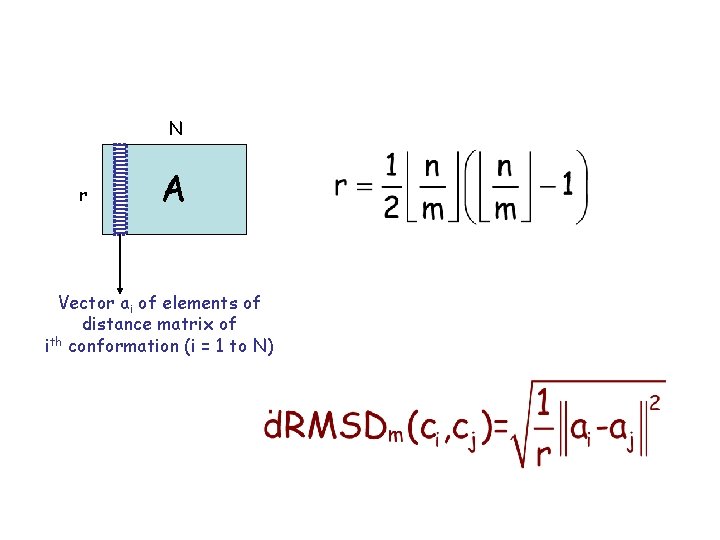
Further Reduction for d. RMSD 1) Stack m-averaged distance matrices as vectors of a matrix A

N r A Vector ai of elements of distance matrix of ith conformation (i = 1 to N)

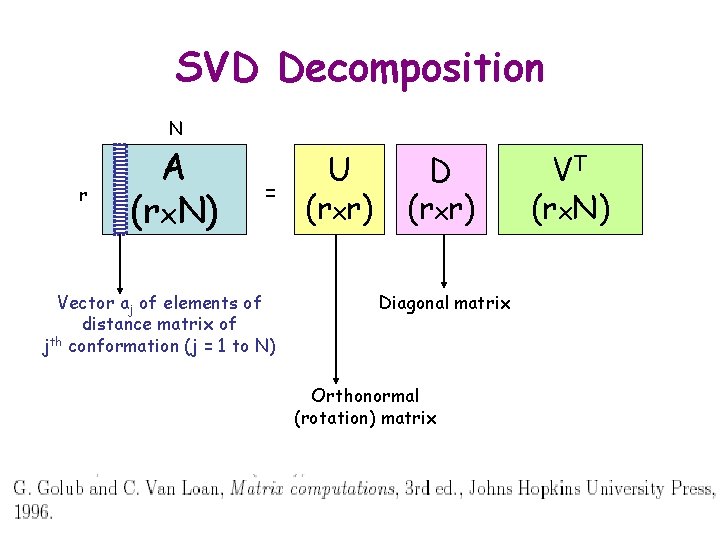
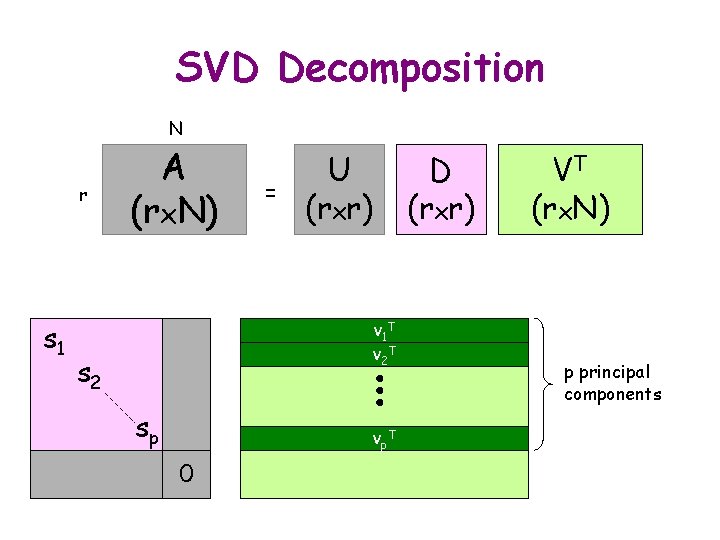
Further Reduction for d. RMSD 1) Stack m-averaged distance matrices as vectors of a matrix A 2) Compute the SVD A = UDVT

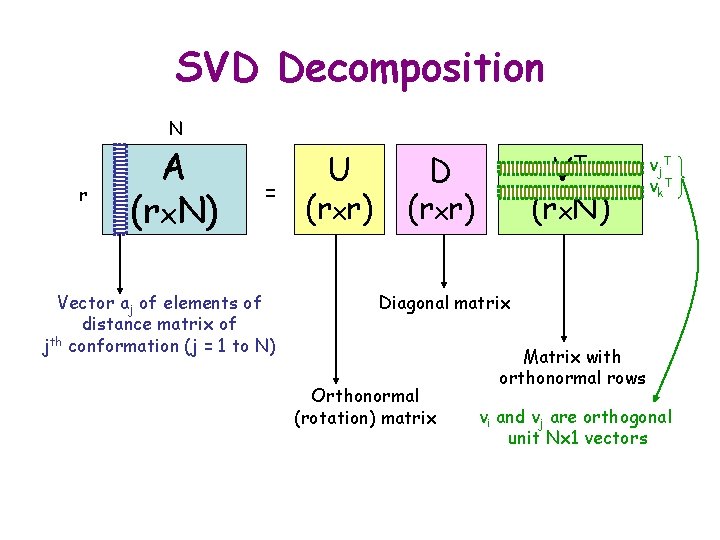
SVD Decomposition N r A (rx. N) = Vector aj of elements of distance matrix of jth conformation (j = 1 to N) U (rxr) Diagonal matrix Orthonormal (rotation) matrix VT (rx. N)

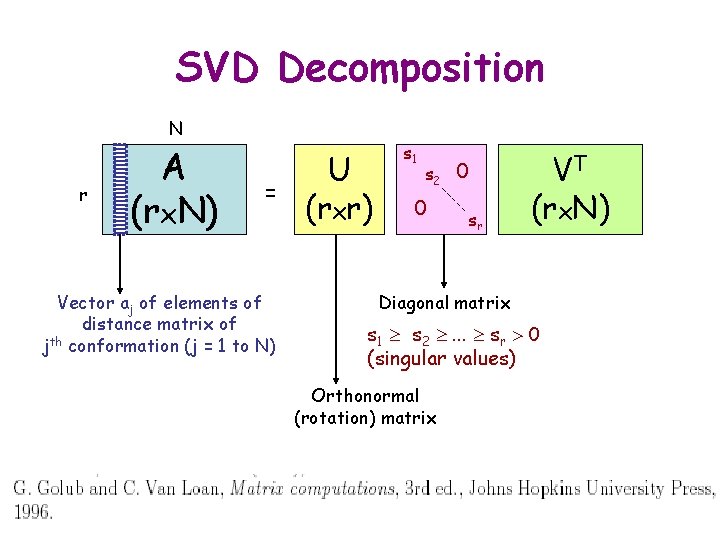
SVD Decomposition N r A (rx. N) = Vector aj of elements of distance matrix of jth conformation (j = 1 to N) U (rxr) s 1 s 2 0 0 sr VT (rx. N) Diagonal matrix s 1 s 2 . . . sr 0 (singular values) Orthonormal (rotation) matrix

SVD Decomposition N r A (rx. N) = Vector aj of elements of distance matrix of jth conformation (j = 1 to N) U (rxr) VT D (rxr) (rx. N) vj. T vk. T Diagonal matrix Orthonormal (rotation) matrix Matrix with orthonormal rows vi and vj are orthogonal unit Nx 1 vectors

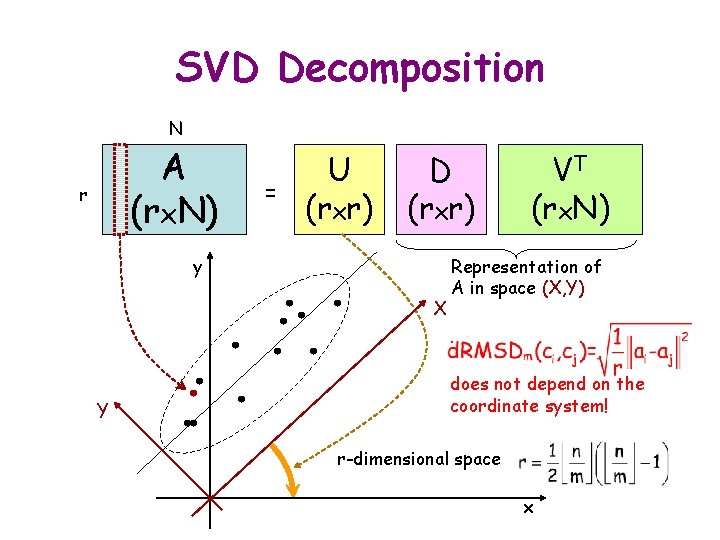
SVD Decomposition N A (rx. N) r = U (rxr) D (rxr) y X Y VT (rx. N) Representation of A in space (X, Y) does not depend on the coordinate system! r-dimensional space x

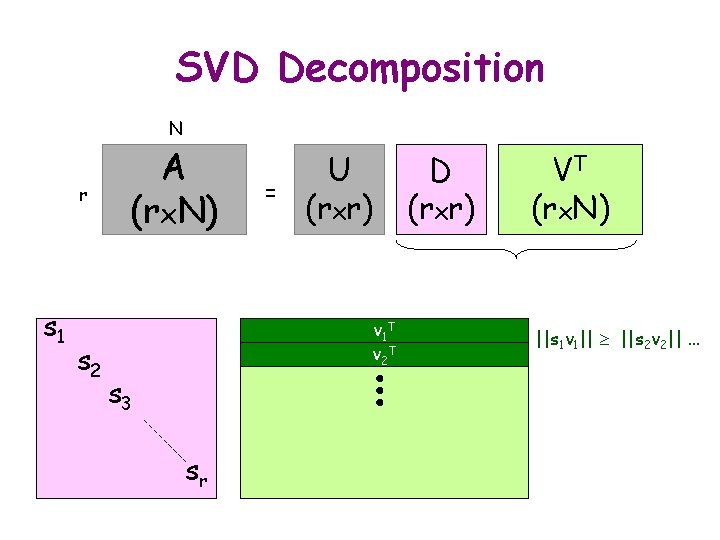
SVD Decomposition N r s 1 s 2 A (rx. N) = U (rxr) v 1 T v 2 T s 3 sr D (rxr) VT (rx. N) ||s 1 v 1|| ||s 2 v 2||. . .

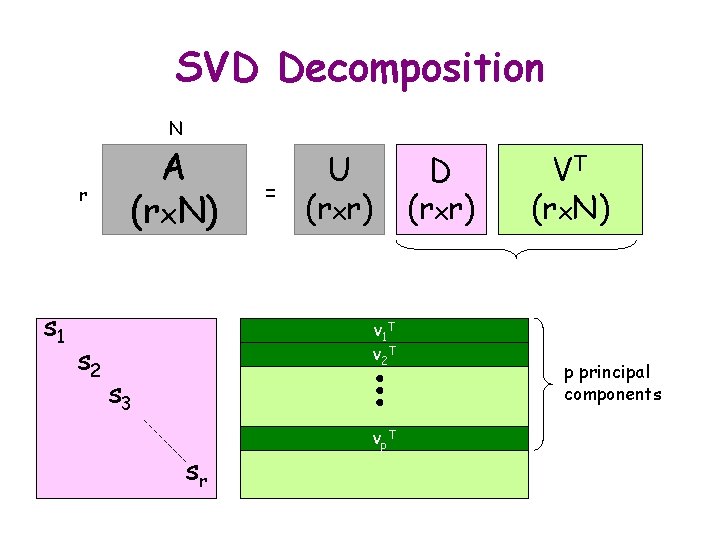
SVD Decomposition N r s 1 s 2 A (rx. N) = U (rxr) v 1 T v 2 T s 3 sr vp T D (rxr) VT (rx. N) p principal components

SVD Decomposition N r s 1 A (rx. N) = U (rxr) v 1 T v 2 T s 2 sp vp T 0 D (rxr) VT (rx. N) p principal components

Further Reduction for d. RMSD 1) Stack m-averaged distance matrices as vectors of a matrix A 2) Compute the SVD A = UDVT 3) Project onto p principal components

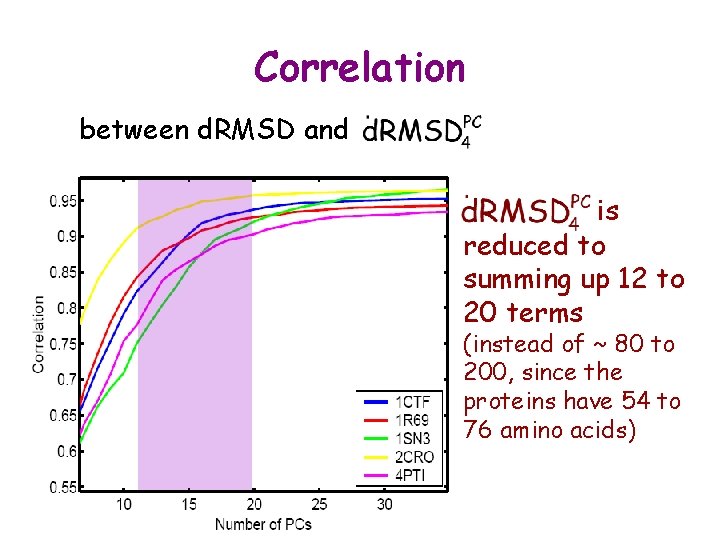
Correlation between d. RMSD and is reduced to summing up 12 to 20 terms (instead of ~ 80 to 200, since the proteins have 54 to 76 amino acids)

Complexity of SVD § SVD of rx. N matrix, where N > r, takes O(r 2 N) time § Here r ~ (n/m)2 § So, time complexity is O(n 4 N) § Would be too costly without m-averaging

Evaluation for 1 CTF Decoy Sets [Lotan and Schwarzer, 2003] § § § § § N = 100, 000, k = 100, 4 -averaging, 16 PCs 70% correct, with furthest NN off by 20% Brute-force: 84 h Brute-force + m-averaging: 4. 8 h Brute-force + m-averaging + PC: 41 min k. D-tree + m-averaging + PC: 19 min Speedup greater than x 200 6 k approximate NNs contain all true k NNs Use m-averaging and PC reduction as fast filters