Conformal Invariance Finiteness and Beta Deformed N4 SYM

Conformal Invariance = Finiteness and Beta Deformed N=4 SYM Theory D. I. Kazakov , L. V. Bork Bogoliubov Lab. JINR (Dubna) & ITEP (Moscow) ITEP & MEPHI (Moscow) ar. Xiv: 0706. 4245 v 1 [hep-th]

N=4 SYM Theory n n N=4 SYM is magnificent playground to test nonperturbative features of QFT. One of them is Ad. S/CFT correspondence (Maldacena’ 98; Polyakov, Gubser, Klebanov’ 98; E. Witten’ 98). Ad. S/CFT requires from the field theory to be conformally invariant and not necessarily obtain the full N=4 supersymmetry.

Marginally deformed N=4 SYM Beta-deformation (Leigh&Strassler’ 95): A supergravity dual to this deformed theory in Ad. S/CFT context was found (Lunin&Maldacena’ 05). Will Beta-deformed N=4 SYM remain conformal invariant on quantum level ( Will loop corrections preserve conformal sym. ) ?

Conformal invariance of Betadeformed N=4 SYM One can reparametrise couplings: and try to find manifold of fixed points order by order in P. T. (Kazakov, Tarasov, Ermushev’ 85; Jones’ 86; Oehme’ 86). One can write (Novikov, Zakharov, Shifman&Vainshtain’ 83): where So one can see that:

Conformal invariance=finiteness 1 -loop Choosing N=1 superspace formalism and background field gauge in dimensional regularization (reduction) and MS-bar scheme one can see that (Zanon and et al. ’ 05; Rossi, Sokatchev, Stanev’ 05; Freedman&Gursoy’ 05): 1 -loop: So at one loop level theory is conformal invariant and finite. What will happen in higher orders of P. T. (how 1 -loop condition will be modified) ?

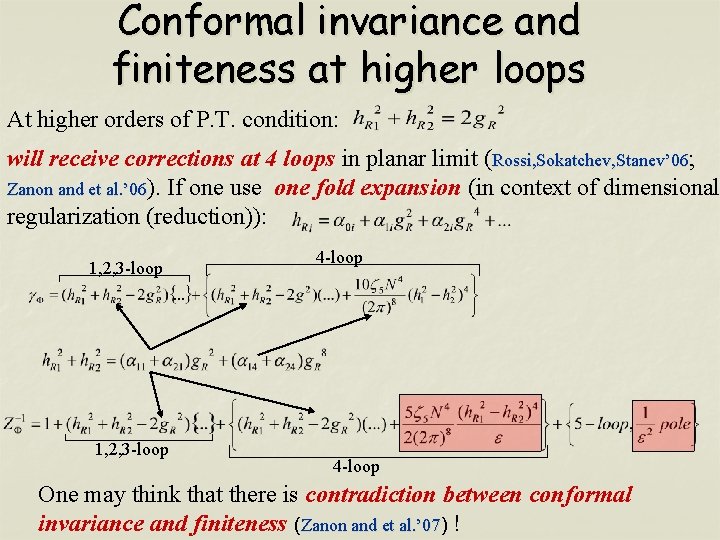
Conformal invariance and finiteness at higher loops At higher orders of P. T. condition: will receive corrections at 4 loops in planar limit (Rossi, Sokatchev, Stanev’ 06; Zanon and et al. ’ 06). If one use one fold expansion (in context of dimensional regularization (reduction)): 1, 2, 3 -loop 4 -loop One may think that there is contradiction between conformal invariance and finiteness (Zanon and et al. ’ 07) al. ’ 07 !

Conformal invariance=finiteness If previous assumptions are satisfied (dimensional regularization (reduction) and MS-bar scheme) then one have two fold expansion (Kazakov’ 85): Or alternatively for bare couplings: Coefficients are defined order by order in P. T. and one can obtain simultaneously finiteness and conformal invariantness in any given order of P. T.

in beta-deformed N=4 SYM up to 4 loops in planar limit Straightforward calculations lead to the following family of solutions : And theory is finite and conformal invariant up to 4 -loops. Using algorithm described here one can make theory finite and conformal invariant at any given order of P. T.

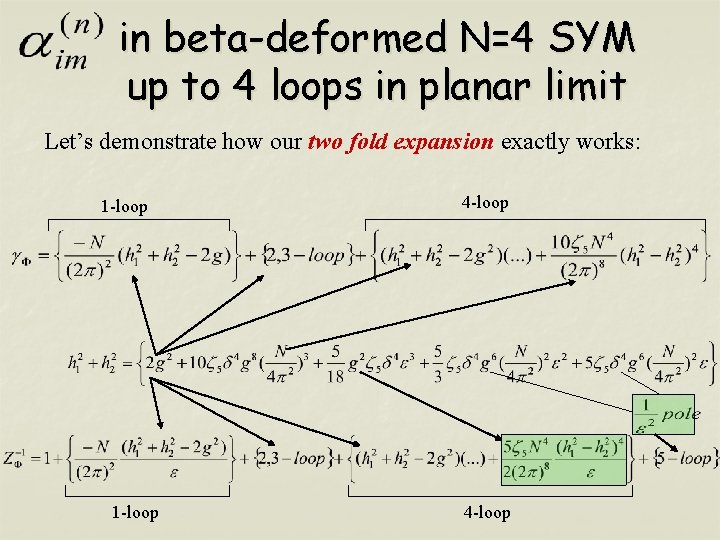
in beta-deformed N=4 SYM up to 4 loops in planar limit Let’s demonstrate how our two fold expansion exactly works: 1 -loop 4 -loop

Conclusions n n n Beta-deformed N=4 SYM can be made simultaneously conformal invariant and finite. In a framework of dimensional regularization ( reduction ) one has to use double series of Yukawa couplings over g and parameter of dimensional regularization. Deformation with complex beta is also allowed.