Confirmatory Factor Analysis Using Open Mx R CFA

Confirmatory Factor Analysis Using Open. Mx & R (CFA) Practical Session Timothy C. Bates

Confirmatory Factor Analysis to test theory • Are there 5 independent domains of personality? • Do domains have facets? • Is Locus of control the same as primary control? • Is prosociality one thing , or three? • Is Grit independent of Conscientiousness?

Prosocial Obligations • Prosociality covers several domains, e. g. – Workplace: voluntary overtime – Civic life: Giving evidence in court – Welfare of others: paying for other’s healthcare • CFA can test the fit of theories – Which hypothesised model fits best? • 3 indicators of one factor? • 3 correlated factors? • 3 independent factors?

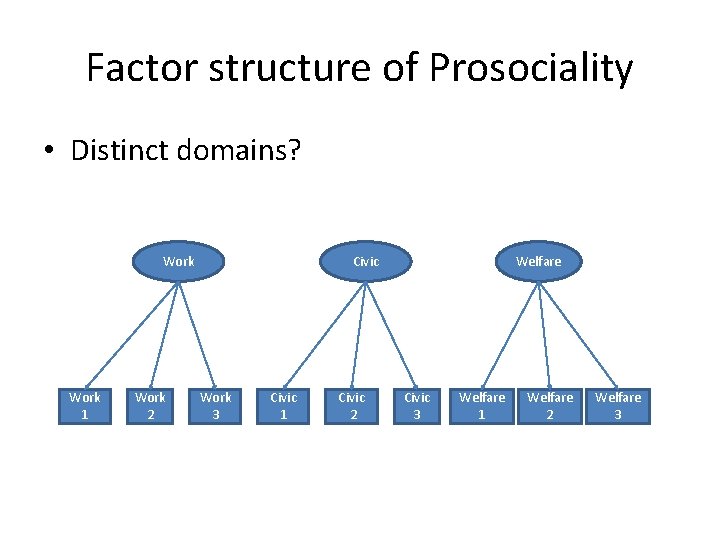
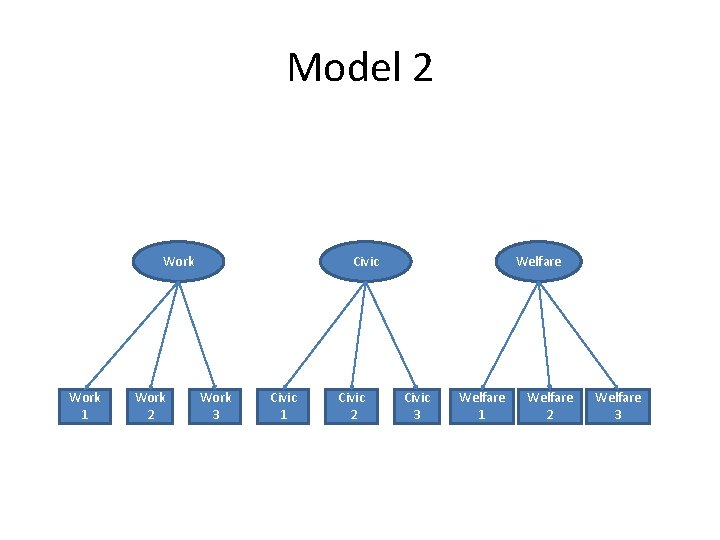
Factor structure of Prosociality • Distinct domains? Work 1 Work 2 Civic Work 3 Civic 1 Civic 2 Welfare Civic 3 Welfare 1 Welfare 2 Welfare 3

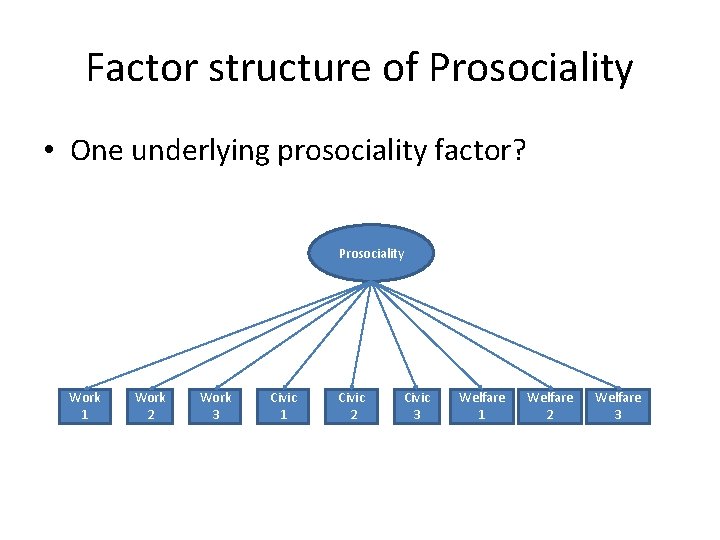
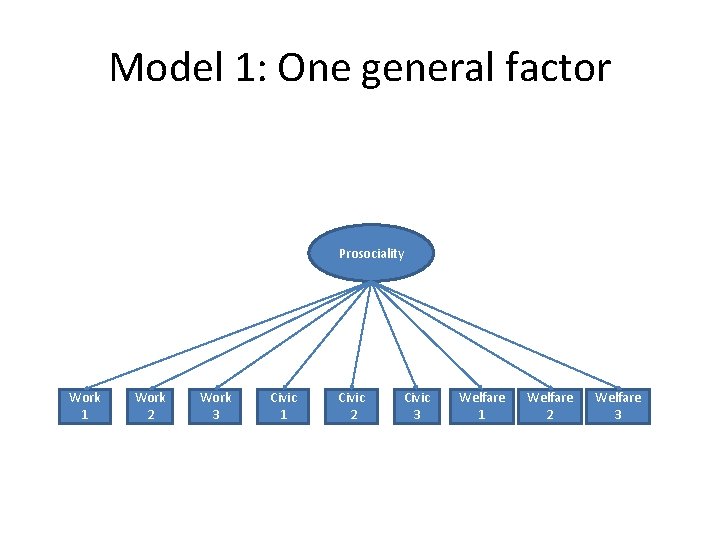
Factor structure of Prosociality • One underlying prosociality factor? Prosociality Work 1 Work 2 Work 3 Civic 1 Civic 2 Civic 3 Welfare 1 Welfare 2 Welfare 3

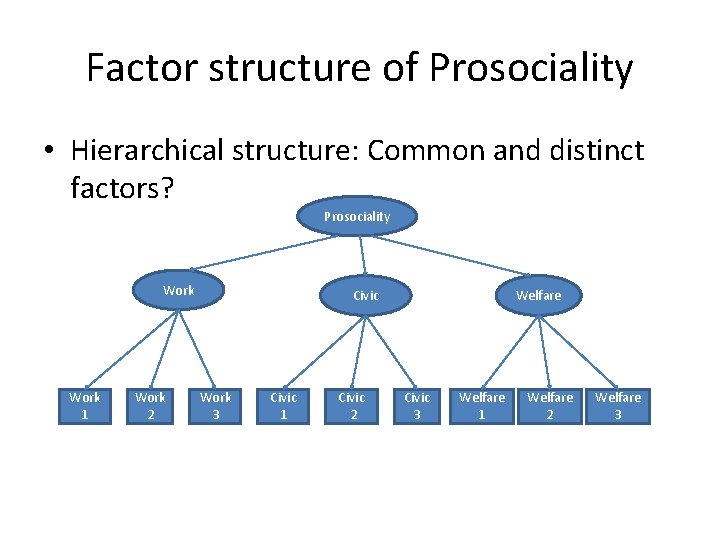
Factor structure of Prosociality • Hierarchical structure: Common and distinct factors? Prosociality Work 1 Work 2 Civic Work 3 Civic 1 Civic 2 Welfare Civic 3 Welfare 1 Welfare 2 Welfare 3

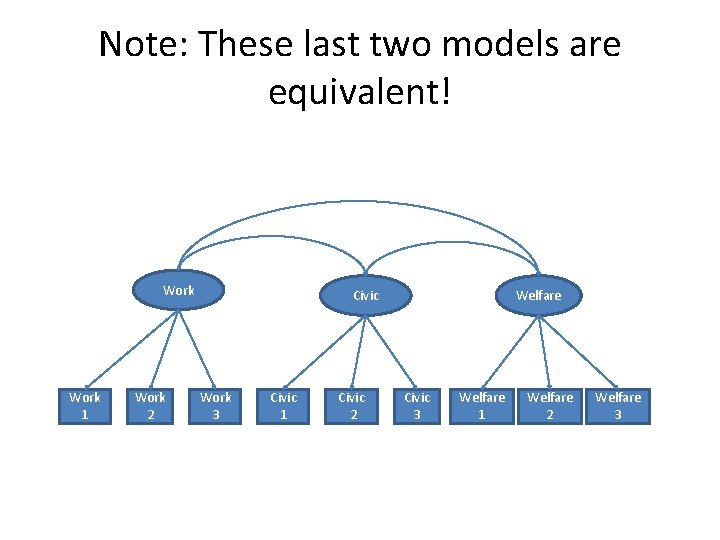
Note: These last two models are equivalent! Work 1 Work 2 Civic Work 3 Civic 1 Civic 2 Welfare Civic 3 Welfare 1 Welfare 2 Welfare 3

CFA with R & Open. Mx • library(Open. Mx) • What is Open. Mx? – “Open. Mx is free and open source software for use with R that allows estimation of a wide variety of advanced multivariate statistical models. ” • Homepage: http: //openmx. psyc. virginia. edu/ • # library(sem)

Our data • Dataset: Midlife Study of Well-Being in the US (Midus) • Prosocial obligations - c. 1000 individuals – How much obligation do you feel… • to testify in court about an accident you witnessed? ’ [civic] • to do more than most people would do on your kind of job? ’ [work] • to pay more for your healthcare so that everyone had access to healthcare? [welfare]

Preparatory code First we need to load Open. Mx require(Open. Mx) Now lets get the data (R can read data off the web) my. Data= read. csv("http: //www. subjectpool. com/prosocial_data. csv") ? What are the names in the data? summary(my. Data) # We have some NAs my. Data= na. omit(my. Data) # imputation is another solution summary(my. Data)

Core Open. Mx functions • mx. Model() – this will contain all the objects in our model – mx. Path(): each path in our model – mx. Data(): the data for the model • mx. Run() – Generate parameter estimates by sending the model to an optimizer – Returns a fitted model

CFA on our competing models • Three competing models to test today: 1. One general factor 2. Three uncorrelated factors 3. Three correlated factors

Model 1: One general factor Prosociality Work 1 Work 2 Work 3 Civic 1 Civic 2 Civic 3 Welfare 1 Welfare 2 Welfare 3

• Quite a bit more code than you have used before: – We’ll go through it step-by-step

Model 1 – Step 1 # Get set up latents = "F 1” manifests = names(my. Data) observed. Cov = cov(my. Data) num. Subjects = nrow(my. Data) # Create a model using the mx. Model function cfa 1<- mx. Model("Common Factor Model”, type="RAM”,

Model 1 – Step 2 # Here we set the measured and latent variables manifest. Vars = manifests, latent. Vars = latents,

Model 1 – Step 3 # Create residual variance for manifest variables using mx. Path( from=manifests, arrows=2, free=T, values=1, labels=paste("error”, 1: 9, sep=“”) ), # using mx. Path, fix the latent factor variance to 1 mx. Path( from="F 1", arrows=2, free=F, values=1, labels ="var. F 1”), # Using mx. Path, specify the factor loadings mx. Path(from="F 1”, to=manifests, arrows=1, free=T, values=1, labels =paste(”l”, 1: 9, sep=“”)),

Model 1 – Step 4 # Give mx. Data the covariance matrix of ‘data 2’ for analysis mx. Data(observed=observed. Cov , type="cov", num. Obs=num. Subjects ) # make sure your last statement DOESN’T have a comma after it ) # Close model

Model 1 – Run the model # The mx. Run function fits the model cfa 1<- mx. Run(cfa 1) # Lets see the summary output summary(cfa 1) # What is in a model? slot. Names(cfa 1@output) names(cfa 1@output)

Summary Output # Ideally, chi-square should be non-significant chi-square: 564. 41; p: <. 001 # Lower is better for AIC and BIC AIC (Mx): 510. 41 BIC (Mx): 191. 47 # <. 06 is good fit: This model is a bad fit RMSEA: 0. 15

Story so far… • Model 1 (one common factor) is a poor fit to the data)

Model 2 Work 1 Work 2 Civic Work 3 Civic 1 Civic 2 Welfare Civic 3 Welfare 1 Welfare 2 Welfare 3

Model 2 – Step 1 # Create a model using the mx. Model function cfa 3<-mx. Model("Three Distinct Factors Model Path Specification", type="RAM",

Model 2 – Step 2 # Here we name the measured variables manifest. Vars=manifests, # Here we name the latent variable latent. Vars=c("F 1", "F 2", "F 3"),

Model 2 – Step 3 # Create residual variance for manifest variables mx. Path(from=manifests, arrows=2, free=T, values=1, labels=c("error”, 1: 9, sep=“”)),

Model 2 – Step 4 # Specify latent factor variances mx. Path(from=c("F 1", "F 2", "F 3"), arrows=2, free=F, values=1, labels=c("var. F 1", "var. F 2", "var. F 3") ),

Model 2 – Step 5 # Fix the covariance between latent factors to zero (i. e. specify the factors as uncorrelated) mx. Path( from="F 1", to="F 2", arrows=2, free=FALSE, values=0, labels="cov 1” ),

Model 2 – Step 6 mx. Path(from="F 1”, to="F 3", arrows=2, free=F, values=0, labels="cov 2"), mx. Path(from="F 2", to="F 3", arrows=2, free=F, values=0, labels="cov 3"),

Model 2 – Step 7 # Specify the factor loading i. e. here we specify that F 1 loads on work 1, 2, and 3 mx. Path( from="F 1", to=c("work 1", "work 2", "work 3"), arrows=1, free=T, values=1, labels=c("l 1", "l 2", "l 3") ), mx. Path( from="F 2", to=c("civic 1", "civic 2", "civic 3"), arrows=1, free=T, values=1, labels=c("l 4", "l 5", "l 6") ),

Model 2 – Step 8 mx. Path( from="F 3", to=c("welfare 1", "welfare 2", "welfare 3"), arrows=1, free=T, values=1, labels=c("l 7", "l 8", "l 9") ), # Use the covariance matrix of ‘my. Data’ for analysis mx. Data(observed=cov(my. Data), type="cov", num. Obs=nrow(my. Data)) ) # Close the model

Model 2 – Run the model # The mx. Run function fits the model three. Distinct. Factor. Fit <- mx. Run(three. Distinctfactor. Model) # The following line will deliver a lot of output two. Factor. Fit@output # Lets see the summary output summary(three. Distinct. Factor. Fit)

Summary Output # Ideally, chi-square should be non-significant chi-square: 576. 50; p: <. 0001 # Lower is better for AIC and BIC AIC (Mx): 522. 50 BIC (Mx): 197. 51 # <. 08 is a reasonable fit: This model is a poor fit RMSEA: 0. 16

Now your turn… Install Open. Mx repos <c('http: //openmx. psyc. virginia. edu/testing/') If you have your laptop: install. packages('Open. Mx', repos=repos) lib <- 'C: /workspace’ install. packages('Open. Mx', repos=repos, lib=lib) library(Open. Mx, lib=lib)