Confirmatory Factor Analysis Confirmatory Factor Analysis Confirmatory factor

Confirmatory Factor Analysis

Confirmatory Factor Analysis Confirmatory factor analysis (CFA) is a type of structural equation modeling (SEM) that deals specifically with the relationships between observed measures or indicators (e. g. , test items, test scores, behavioral observation ratings) and latent variables or factors. CFA is used to verify the number of underlying dimensions of the instrument (factors) and the pattern of item–factor relationships (factor loadings) CFA is an analytic tool for construct validation in the social and behavioral sciences.

Factor A factor is an unobservable variable that influences more than one observed measure and that accounts for the correlations among these observed measures. The observed measures are intercorrelated because they share a common cause (i. e. , they are influenced by the same underlying construct);

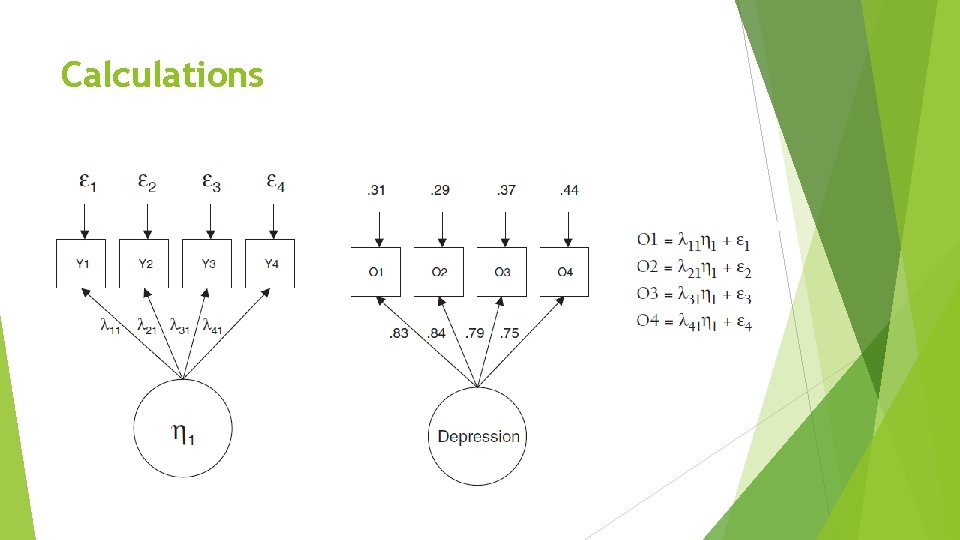
Calculations

Guidelines for Interpreting Goodness‑of‑Fit Indices The latent variable (factor) of Depression is depicted by a circle or an oval, whereas the four clinical ratings (indicators) are represented by squares or rectangles. The unidirectional arrows (→) represent the factor loadings (λ, or lambda), which are the regression slopes (direct effects) for predicting the indicators from the factor (η, or eta). These arrows are also used to relate the unique variances (ε, or epsilon) to the indicators.

Guidelines for Interpreting Goodness‑of‑Fit Indices Hu and Bentler (1999) suggest the following guidelines: 1. SRMR values are close to. 08 or below 2. RMSEA values are close to. 06 or below 3. CFI and TLI (NNFI in Lisrel) values are close to. 95 or greater.

Guidelines for Interpreting Goodness‑of‑Fit Indices Browne and Cudeck (1993) suggest, as a rule of thumb, that RMSEA values less than 0. 08 suggest adequate model fit (i. e. , a “reasonable error of approximation, ” p. 144); that RMSEA values less than 0. 05 suggest good model fit; and that models with RMSEA ≥ 0. 1 should be rejected

Guidelines for Interpreting Goodness‑of‑Fit Indices Methodologists have noted that while CFI and TLI values below. 90 should lead the researcher to strongly suspect (reject) the solution, CFI and TLI values in the range of. 90 and. 95 may be indicative of acceptable model fit (e. g. , Bentler, 1990).

Modification Indices The modification index reflects an approximation of how much the overall mode c 2 will decrease if the fixed or constrained parameter is freely estimated. Because the modification index can be conceptualized as a c 2 statistic with 1 df, indices of 3. 84 or greater (which reflects the critical value of c 2 at p <. 05, 1 df) suggest that the overall fit of the model can be significantly improved (p <. 05).

Unnecessary Parameters Models can be revised by eliminating statistically nonsignificant parameters.

Correlated Errors When no correlated errors (error covariances) are specified, the researcher is asserting that all of the covariation among indicators loading on a given factor is due to that latent dimension (and that all measurement error is random). Correlated errors between indicators are specified on the basis of the notion that some of the covariance in the indicators not explained by the latent variable is due to another exogenous common cause. In the case of the analysis of multiple questionnaire items, correlated errors may arise from items that are very similarly worded, reverseworded, differentially prone to social desirability, or the like.

Correlated Errors Type Set error covariance between Variable 1 and Variable 2 free

Reporting CFA

Reporting CFA

References

Video Lectures https: //www. youtube. com/watch? v=is. DGTLuhdvg https: //www. youtube. com/watch? v=cc. NSZ 7_eqns