Configuring a LoadBalanced Switch in Hardware Srikanth Arekapudi

Configuring a Load-Balanced Switch in Hardware Srikanth Arekapudi, Shang-Tse (Da) Chuang, Isaac Keslassy, Nick Mc. Keown Stanford University

Outline Load Balanced Switch Ø Scalability Ø Reconfiguration Algorithm Ø Hardware Implementation Ø 2

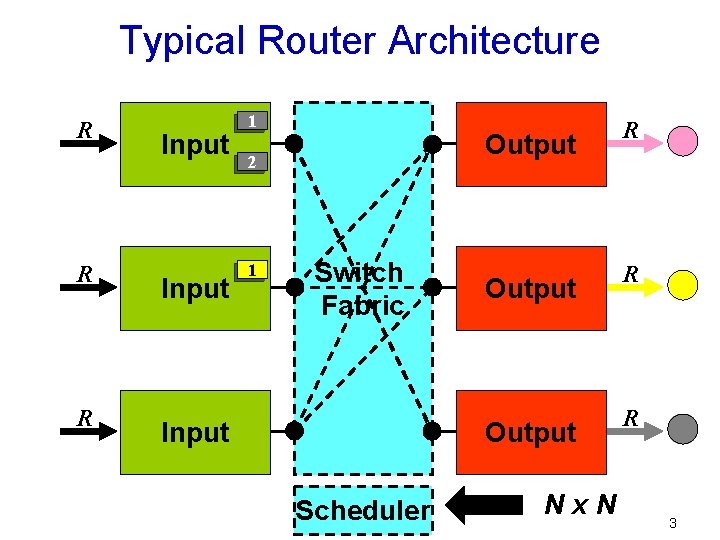
Typical Router Architecture R R R Input 1 Output 2 1 Switch Fabric Input Output Scheduler Nx. N R R R 3

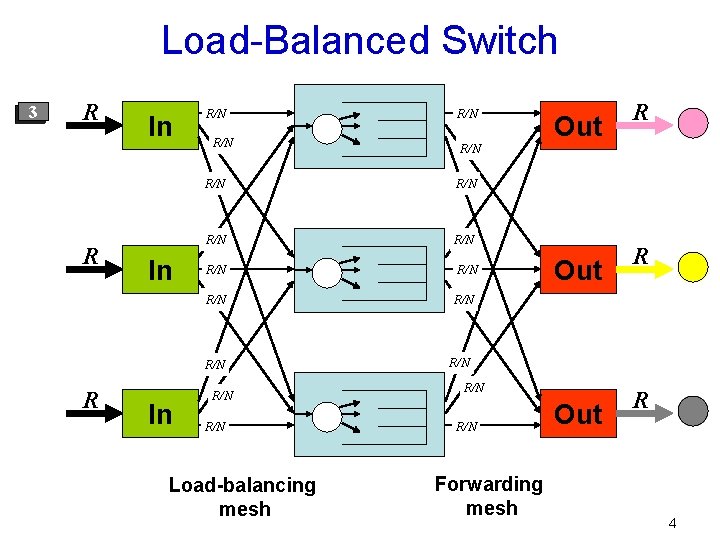
Load-Balanced Switch 123 R R In In R/N R/N In R/N Load-balancing mesh Out R R/N R/N R/N Forwarding mesh 4

Load-Balanced Switch R R In In R/N R/N 1 R/N R/N R/N 2 In Load-balancing mesh R Out R R/N R/N Out R/N R R R/N R/N Out 3 R/N Forwarding mesh 5

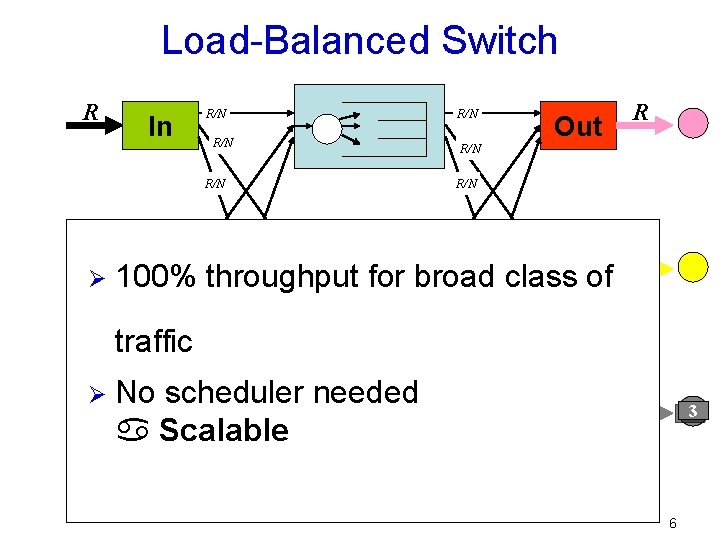
Load-Balanced Switch R R Ø In R/N Out R/N R/N In R/N Out 100% throughput for broad class of traffic R/N No scheduler needed In a Scalable R/N Load-balancing mesh R R/N R/N RØ R/N R/N R/N Forwarding mesh Out R 3 6

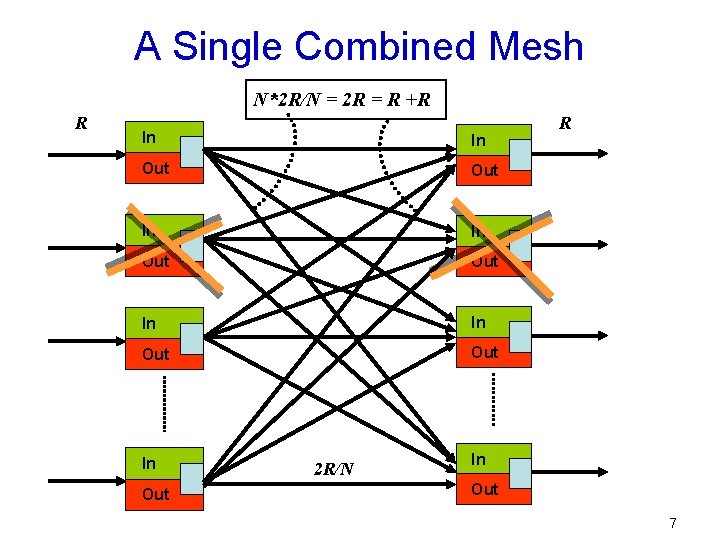
A Single Combined Mesh N*2 R/N = 2 R = R +R R In In Out Out In In Out 2 R/N R In Out 7

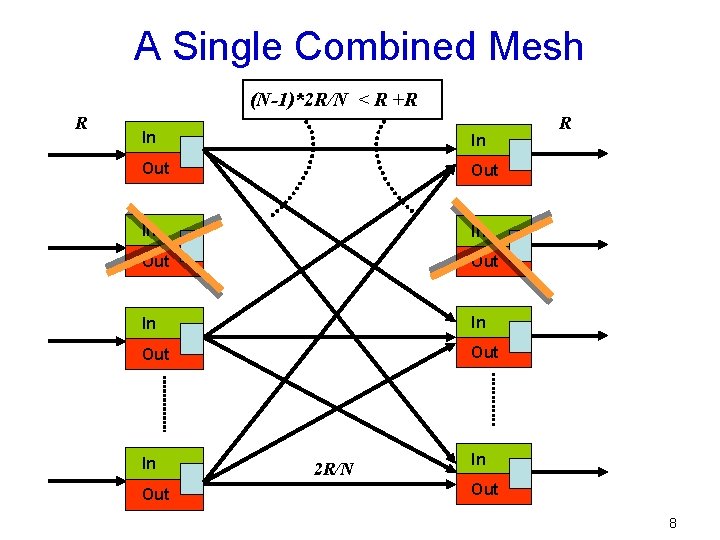
A Single Combined Mesh (N-1)*2 R/N < R +R R In In Out Out In In Out 2 R/N R In Out 8

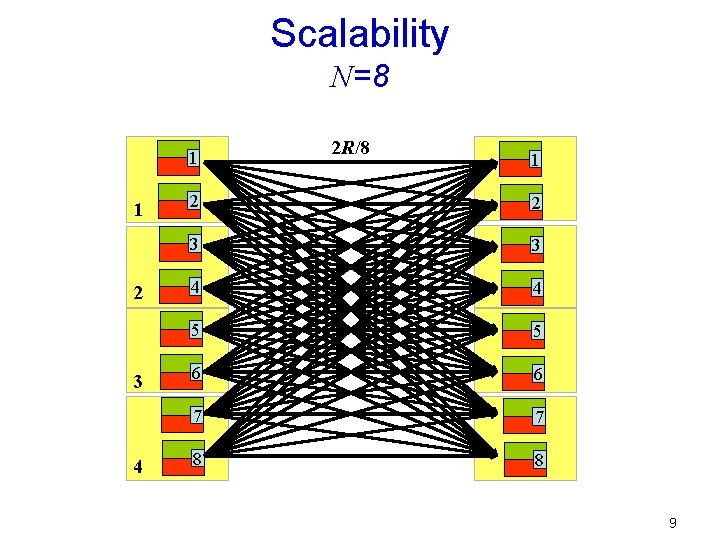
Scalability N=8 1 1 2 3 4 2 R/8 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9

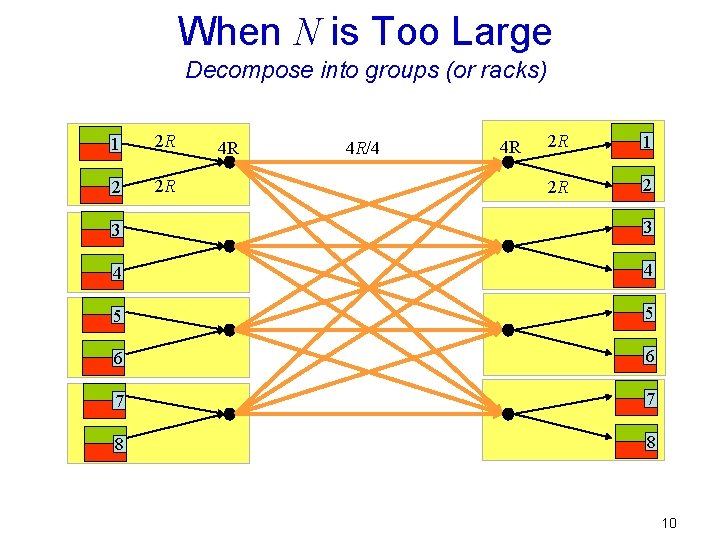
When N is Too Large Decompose into groups (or racks) 1 2 R 2 2 R 4 R 4 R/4 4 R 2 R 1 2 R 2 3 3 4 4 5 5 6 6 7 7 8 8 10

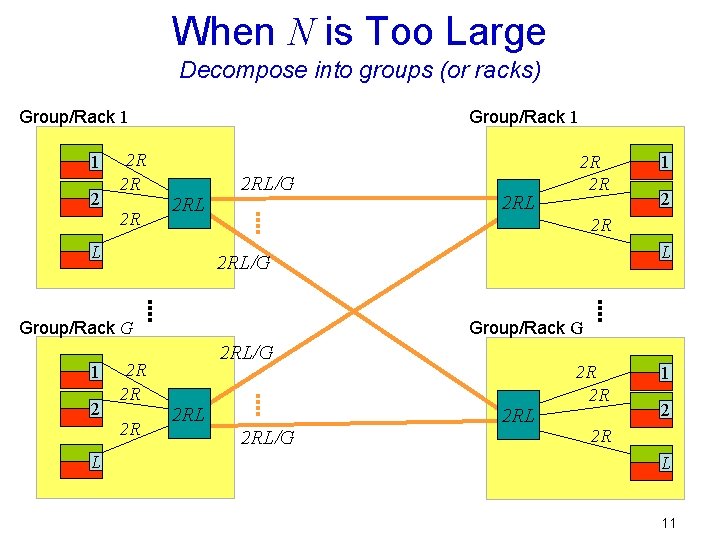
When N is Too Large Decompose into groups (or racks) Group/Rack 1 1 2 2 R 2 R 2 R Group/Rack 1 2 RL L 2 RL/G 2 2 R L 2 RL/G 2 R 2 R 1 2 R Group/Rack G 1 2 RL 2 R 2 R Group/Rack G 2 RL/G 2 RL 2 R 2 R 1 2 2 R L 11

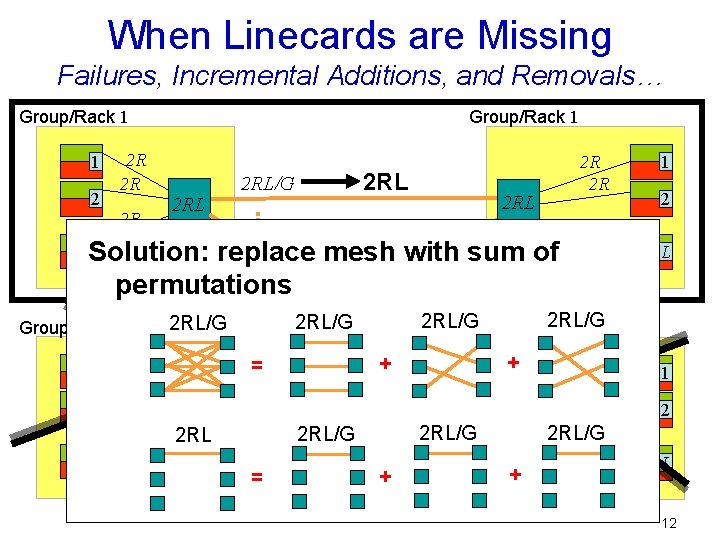
When Linecards are Missing Failures, Incremental Additions, and Removals… Group/Rack 1 1 2 2 R 2 R 2 R Group/Rack 1 2 RL 2 RL/G 2 R 2 R 2 RL 1 2 2 R 2 R 2 R L 2 RL/G = 2 RL 2 2 R L Solution: replace mesh with sum of 2 RL/G permutations Group/Rack G 1 2 RL/GGroup/Rack G 2 RL/G + + 2 RL/G = L + 2 R 2 R 1 2 2 RL/G 2 R L 12

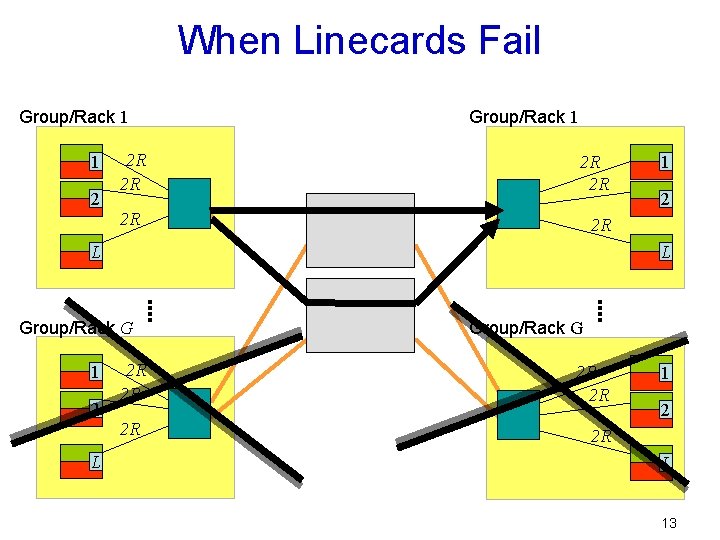
When Linecards Fail Group/Rack 1 1 2 2 R 2 R 2 R L Group/Rack G 1 2 2 R 2 R 2 R L Group/Rack 1 2 R 2 R MEMS Switch 1 2 2 R L Group/Rack G 2 R 2 R 1 2 2 R L 13

Questions Ø Number of MEMS Switches? Ø TDM Schedule? 14

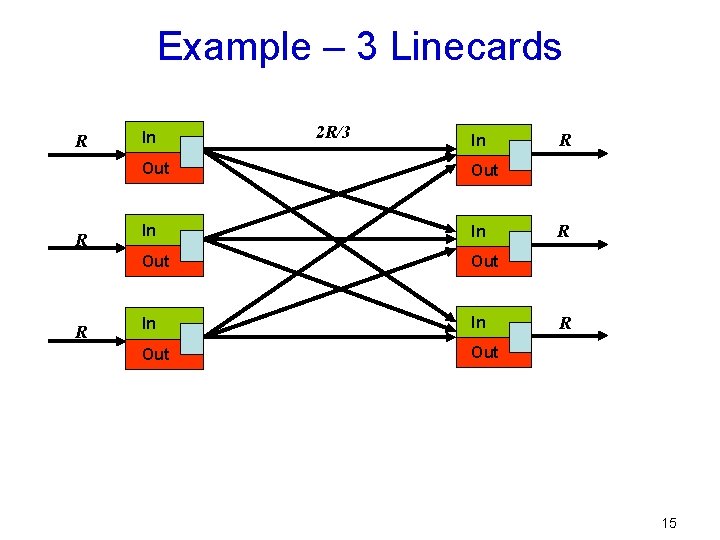
Example – 3 Linecards R R R In 2 R/3 In Out Out In In Out R R R 15

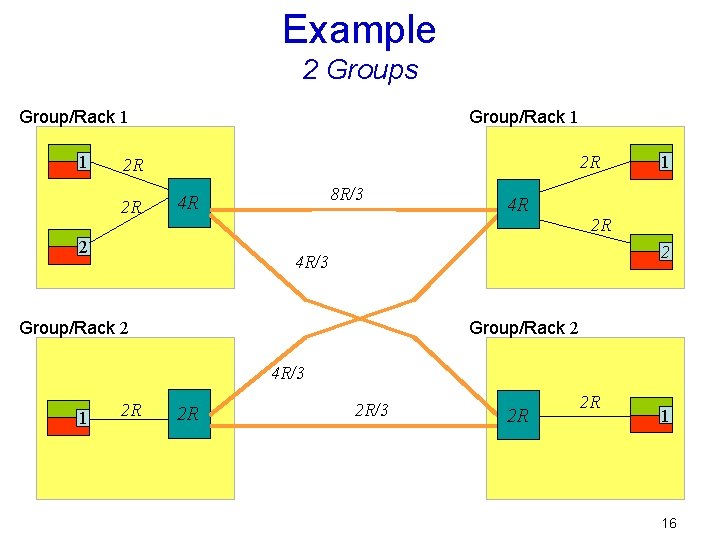
Example 2 Groups Group/Rack 1 1 Group/Rack 1 2 R 2 R 2 R 8 R/3 4 R 2 4 R 1 2 R 2 4 R/3 Group/Rack 2 4 R/3 1 2 R 2 R 2 R/3 2 R 2 R 1 16

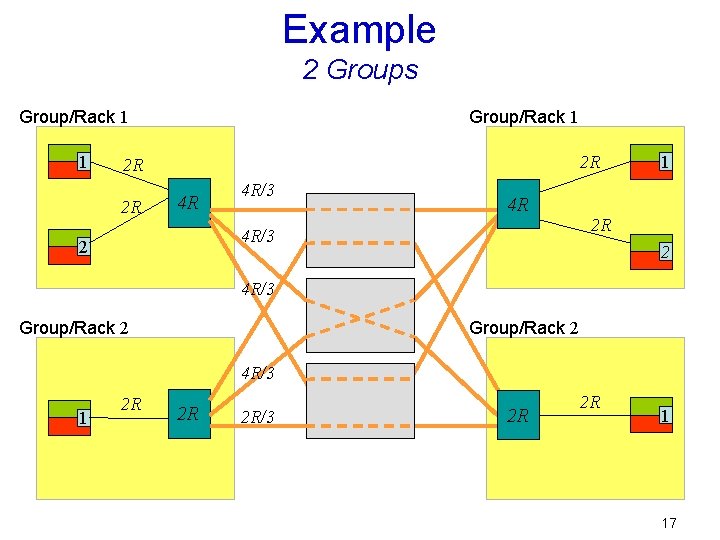
Example 2 Groups Group/Rack 1 1 Group/Rack 1 2 R 2 R 2 R 4 R 4 R/3 2 1 2 R 2 4 R/3 Group/Rack 2 4 R/3 1 2 R 2 R 2 R/3 2 R 2 R 1 17

Number of MEMS Switches Ø MEMS switches between groups i and j Ø Total Number of MEMS switches: M ≤ L+G-1 18

Questions Ø Number of MEMS Switches? Ø TDM Schedule? 19

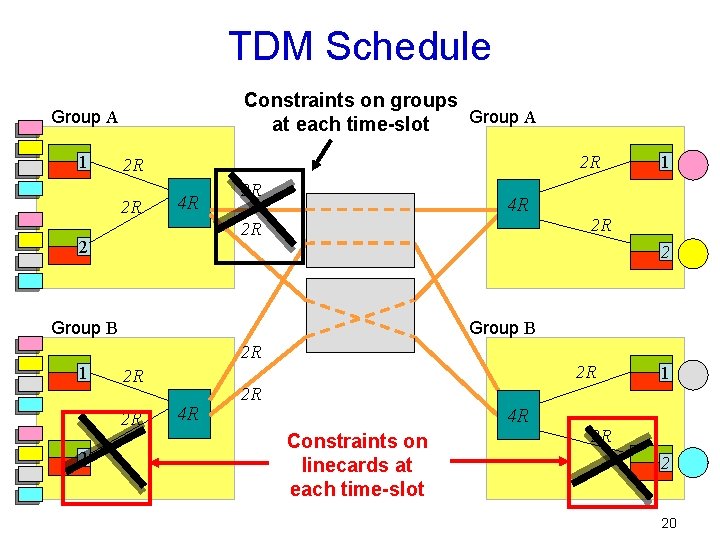
TDM Schedule Constraints on groups Group A at each time-slot Group A 1 2 R 2 R 2 R 4 R 2 R 2 Group B 2 R 2 R 2 R 2 Group B 1 1 4 R 2 R 1 2 R 4 R Constraints on linecards at each time-slot 2 R 2 20

Rules for TDM Schedule At each time-slot: Ø Each transmitting linecard sends one packet Ø Each receiving linecard receives one packet Ø (MEMS constraint) Each transmitting group i sends at most one packet to each receiving group j through each MEMS connecting them In a schedule of N time-slots: Ø Each transmitting linecard sends exactly one packet to each receiving linecard 21

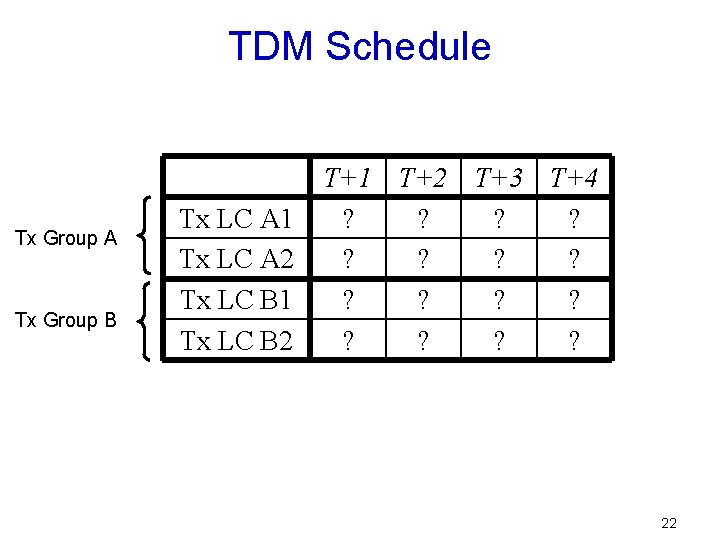
TDM Schedule Tx Group A Tx Group B Tx LC A 1 Tx LC A 2 Tx LC B 1 Tx LC B 2 T+1 T+2 T+3 T+4 ? ? ? ? 22

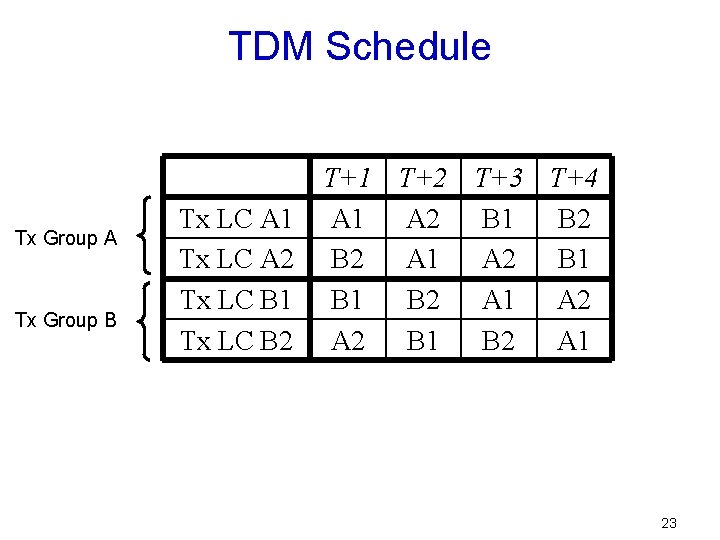
TDM Schedule Tx Group A Tx Group B Tx LC A 1 Tx LC A 2 Tx LC B 1 Tx LC B 2 T+1 T+2 T+3 T+4 A 1 A 2 B 1 B 2 A 1 A 2 B 1 B 2 A 1 23

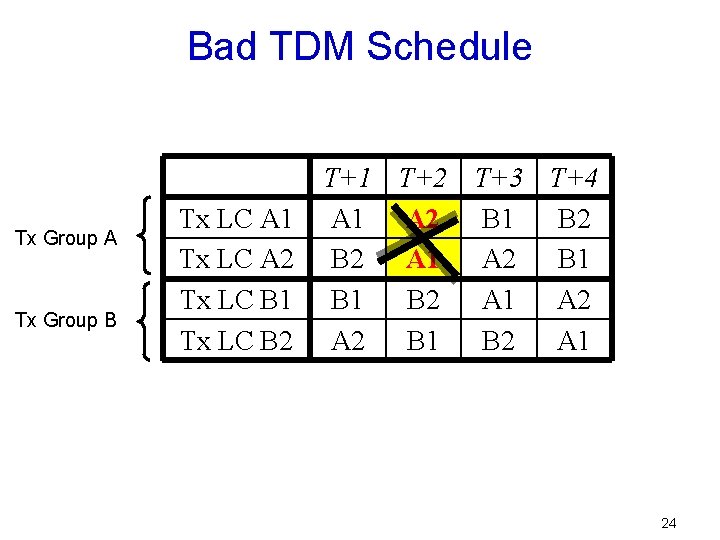
Bad TDM Schedule Tx Group A Tx Group B Tx LC A 1 Tx LC A 2 Tx LC B 1 Tx LC B 2 T+1 T+2 T+3 T+4 A 1 A 2 B 1 B 2 A 1 A 2 B 1 B 2 A 1 24

TDM Schedule Algorithm Ø The algorithm constructs three consecutive schedules. 1. Sending Groups to Receiving Groups • Connection Assignment Problem 2. Sending Linecards to Receiving Groups. • Matrix Decomposition Problem 3. Sending Linecards to Receiving Linecards • Matrix Decomposition Problem 25

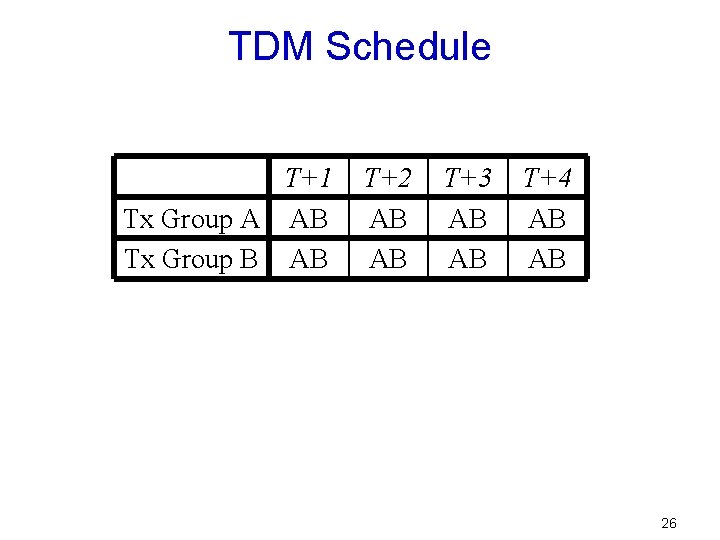
TDM Schedule T+1 Tx Group A AB Tx Group B AB T+2 AB AB T+3 AB AB T+4 AB AB 26

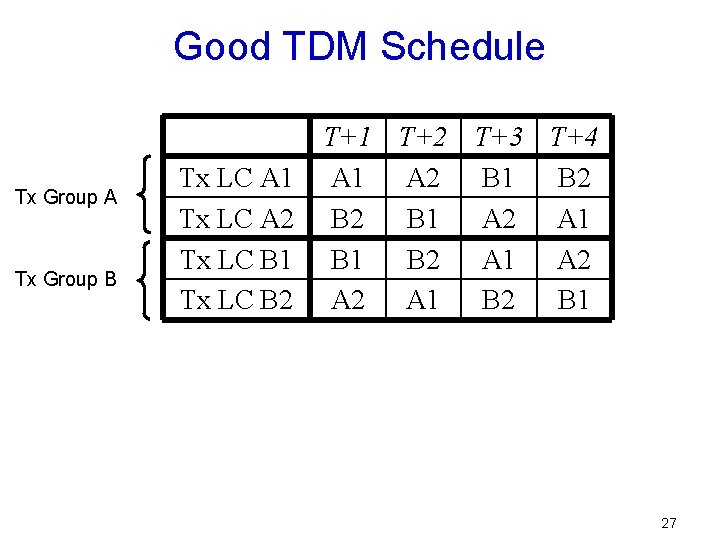
Good TDM Schedule Tx Group A Tx Group B Tx LC A 1 Tx LC A 2 Tx LC B 1 Tx LC B 2 T+1 T+2 T+3 T+4 A 1 A 2 B 1 B 2 B 1 A 2 A 1 B 2 A 1 A 2 A 1 B 2 B 1 27

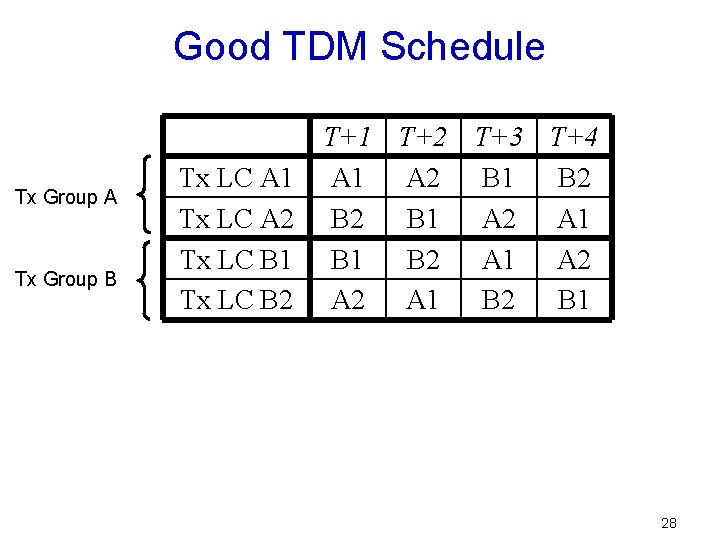
Good TDM Schedule Tx Group A Tx Group B Tx LC A 1 Tx LC A 2 Tx LC B 1 Tx LC B 2 T+1 T+2 T+3 T+4 A 1 A 2 B 1 B 2 B 1 A 2 A 1 B 2 A 1 A 2 A 1 B 2 B 1 28

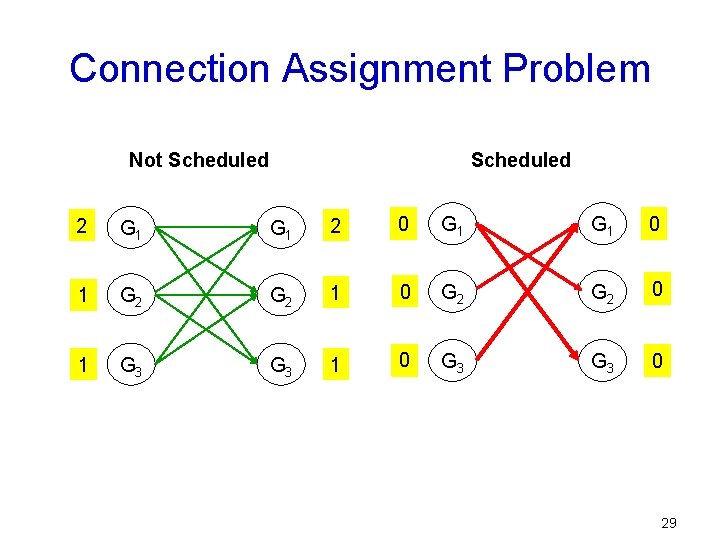
Connection Assignment Problem Not Scheduled 2 G 1 2 0 G 1 0 1 G 2 1 1 0 G 2 1 0 1 G 3 G 3 0 29

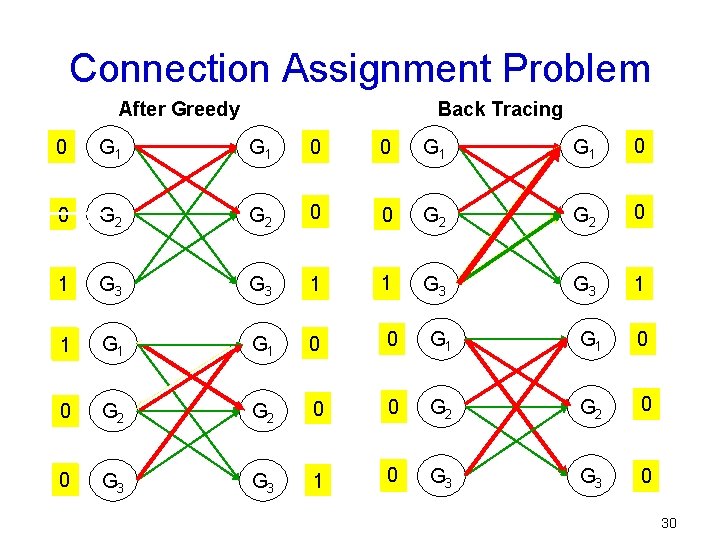
Connection Assignment Problem After Greedy Back Tracing 0 G 1 G 1 0 1 0 G 2 G 2 1 0 1 G 3 G 3 1 01 G 1 0 0 G 1 0 1 0 G 2 G 2 1 0 0 1 G 3 1 0 1 G 3 0 30

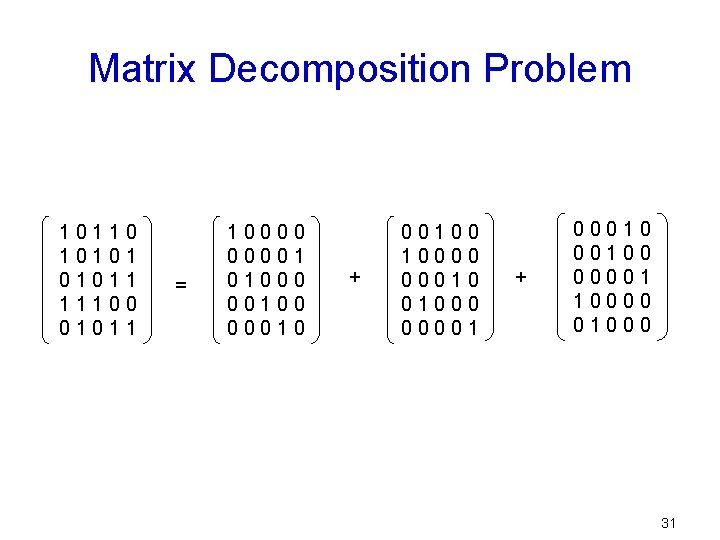
Matrix Decomposition Problem 10110 101011 11100 01011 = 100001 01000 00100 00010 + 00100 10000 00010 01000 00001 + 000100 00001 10000 01000 31

Matrix Decomposition Problem Ø Ø Use of sparsity of matrices to represent the ones as a row-column pair Consists of two stages Ø Ø Greedy Algorithm Slepian-Duguid Algorithm 1. Decomposes all the permutation matrices at once 2. Uses the row-column pair list structure 32

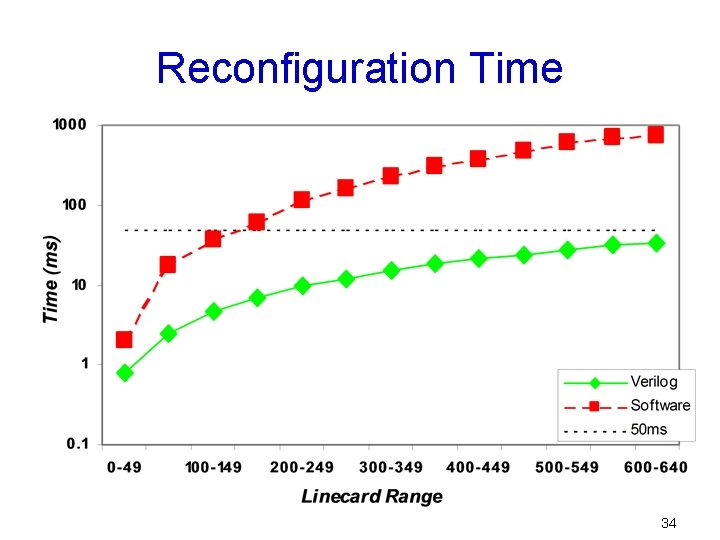
Synthesis Ø Ø Ø 40 Groups and 640 Linecards 0. 13 u process Cycle time within 4 ns Connection Assignment Problem 1. 10 K gates 2. 24 Kbits memory Matrix Decomposition Problem 1. 25 K gates 2. 230 Kbits of memory 33

Reconfiguration Time 34

Thank you.