Configuration Space Kris Hauser Assistant Professor of Computer

Configuration Space Kris Hauser Assistant Professor of Computer Science Indiana University

Readings • Ch 3. 1 -3. 4 • * A Simple Motion-Planning Algorithm for General Robot Manipulators, T. Lozano-Perez, 1987. • * Spatial Planning: a Configuration Space Approach, T. Lozano-Perez, 1980.

Agenda • Introduce configuration spaces (C-spaces) • Lab 1: Install Robot. Sim

Definitions • Workspace: • The world in which a robot lives and occupies space • Usually 2 D (mobile robots) or 3 D (most other robots)

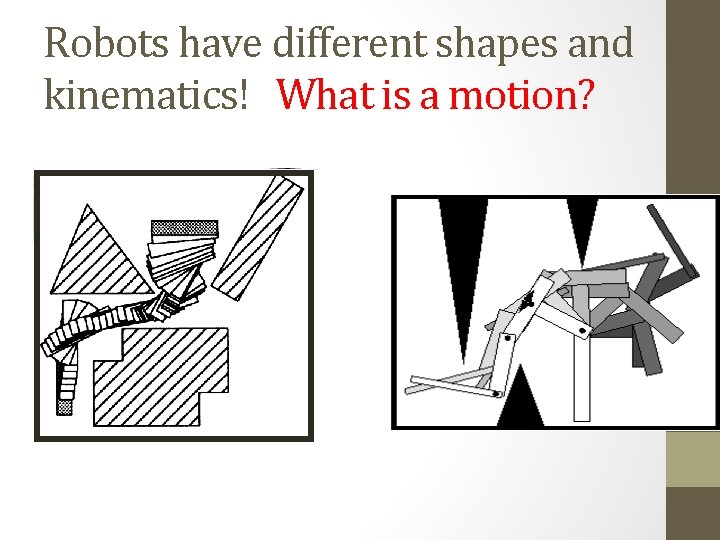
Robots have different shapes and kinematics! What is a motion?

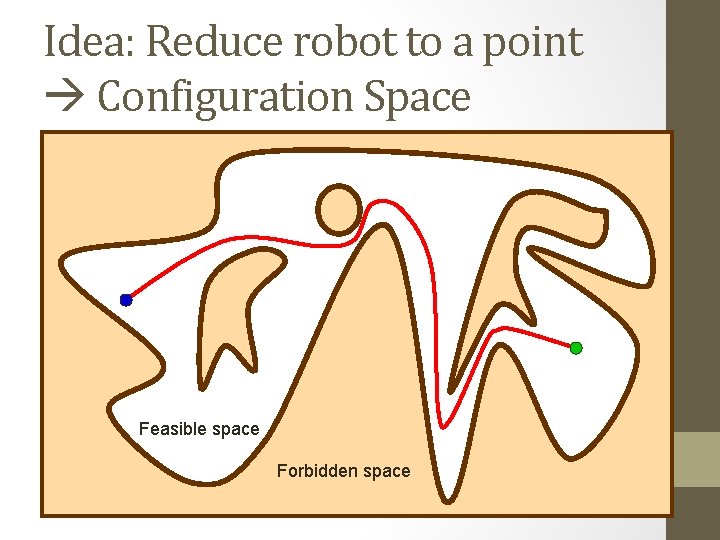
Idea: Reduce robot to a point Configuration Space Feasible space Forbidden space

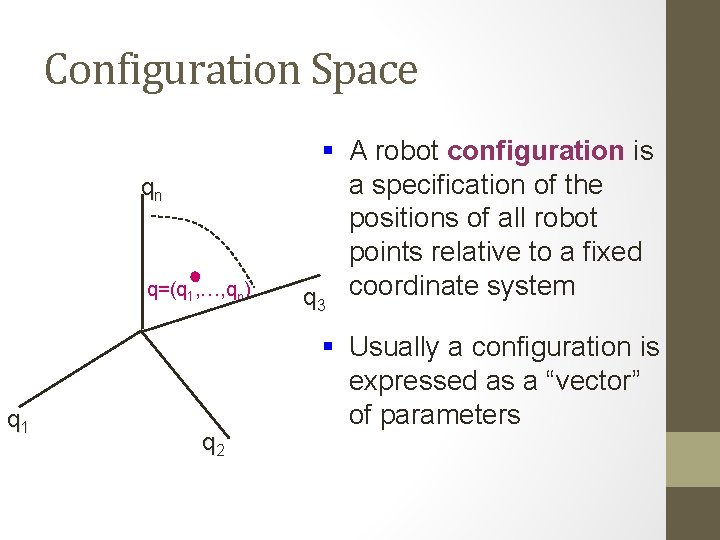
Configuration Space qn q=(q 1, …, qn) q 1 q 2 § A robot configuration is a specification of the positions of all robot points relative to a fixed q coordinate system 3 § Usually a configuration is expressed as a “vector” of parameters

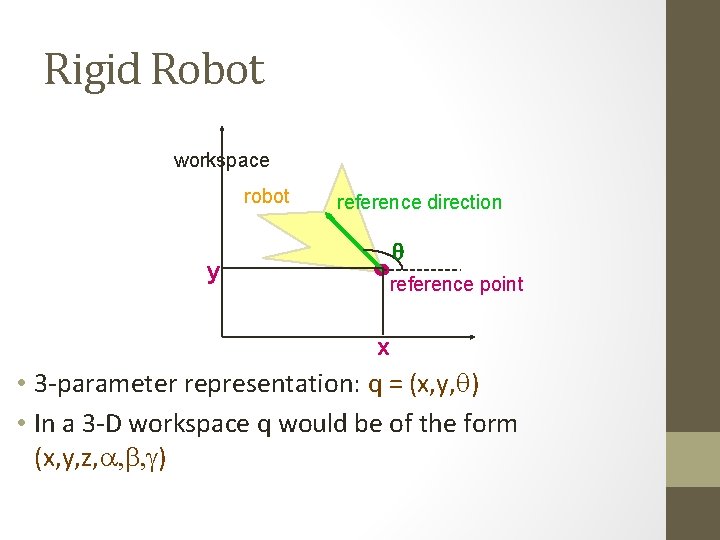
Rigid Robot workspace robot y reference direction q reference point x • 3 -parameter representation: q = (x, y, q) • In a 3 -D workspace q would be of the form (x, y, z, a, b, g)

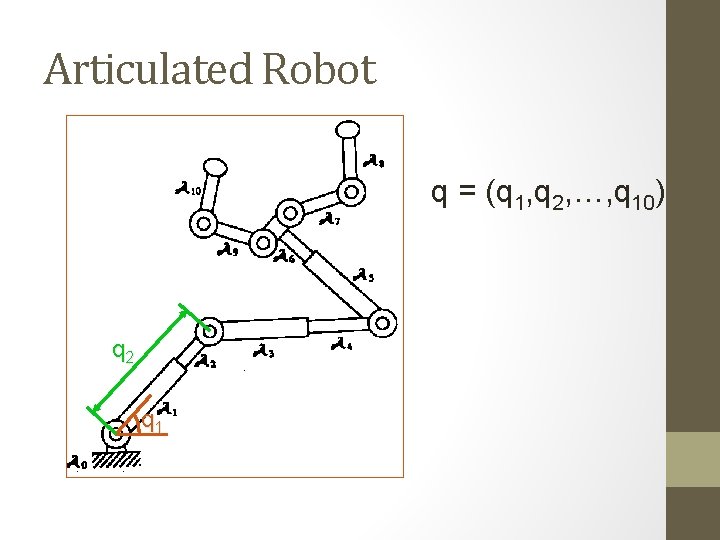
Articulated Robot q = (q 1, q 2, …, q 10) q 2 q 1

Protein

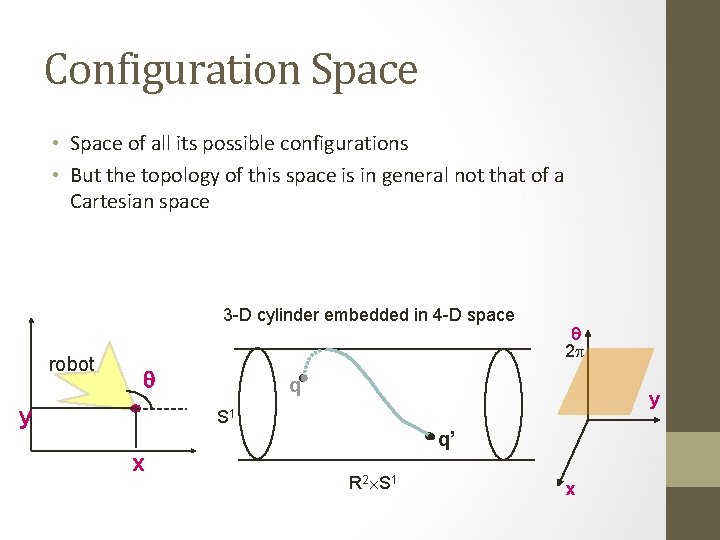
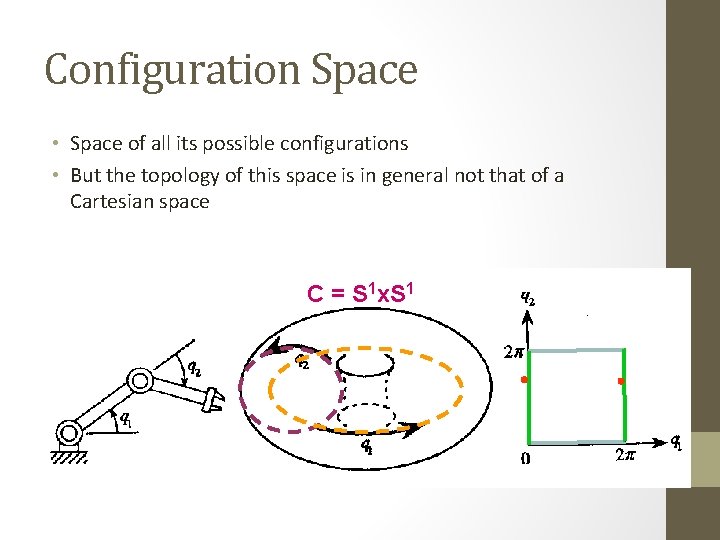
Configuration Space • Space of all its possible configurations • But the topology of this space is in general not that of a Cartesian space 3 -D cylinder embedded in 4 -D space robot q y q 2 p q y S 1 x q’ R 2 S 1 x

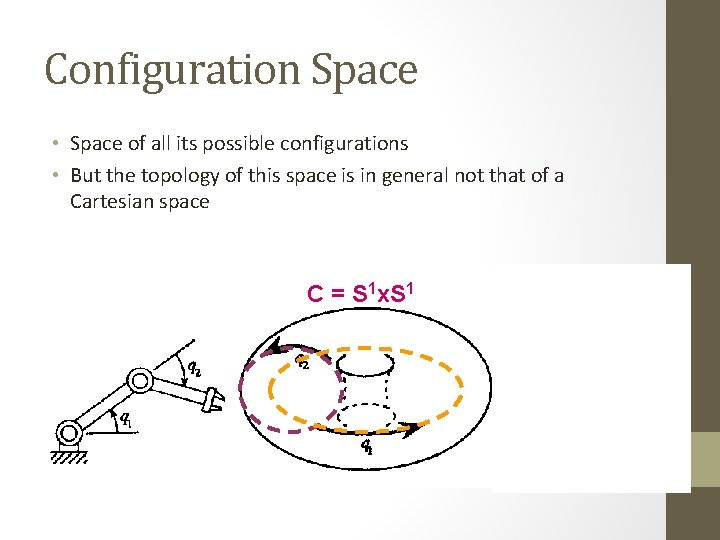
Configuration Space • Space of all its possible configurations • But the topology of this space is in general not that of a Cartesian space C = S 1 x S 1

Configuration Space • Space of all its possible configurations • But the topology of this space is in general not that of a Cartesian space C = S 1 x. S 1

Configuration Space • Space of all its possible configurations • But the topology of this space is in general not that of a Cartesian space C = S 1 x. S 1

Some Important Topological Spaces • • • R: real number line Rn: N-dimensional Cartesian space S 1: boundary of circle in 2 D S 2: surface of sphere in 3 D SO(2), SO(3): set of 2 D, 3 D orientations (special orthogonal group) SE(2), SE(3): set of rigid 2 D, 3 D translations and rotations (special Euclidean group) • Cartesian product A x B, power notation An = A x A … x A • Homeomorphism ~ denotes topological equivalence • • Continuous mapping with continuous inverse (bijective) Cube ~ S 2 SO(2) ~ S 1 SE(3) ~ SO(3) x R 3

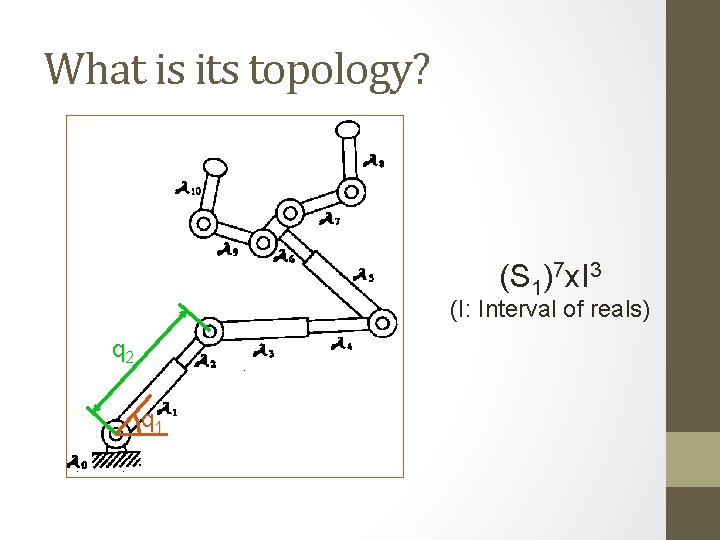
What is its topology? (S 1)7 x. I 3 (I: Interval of reals) q 2 q 1

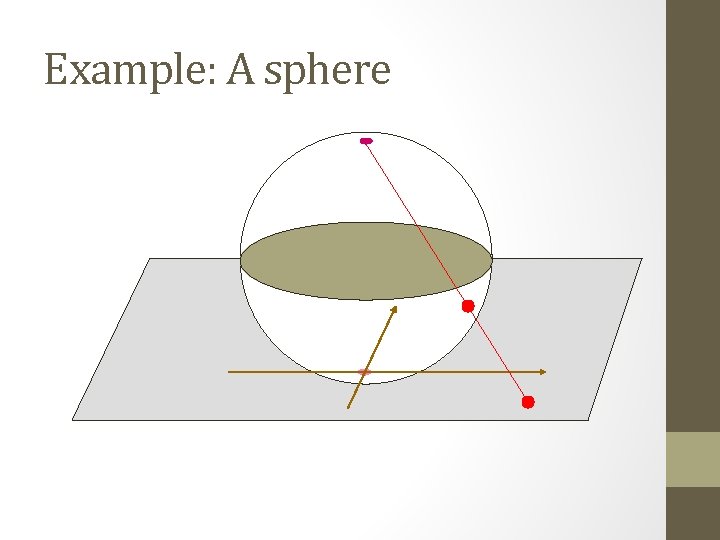
Structure of Configuration Space • It is a manifold, i. e. , for each point q, there is a 1 -to-1 map between a neighborhood of q and a Cartesian space Rn, where n is the dimensionality of C • This map is a local coordinate system called a chart. • C can always be covered by a finite number of charts. Such a set is called an atlas

Example: A sphere

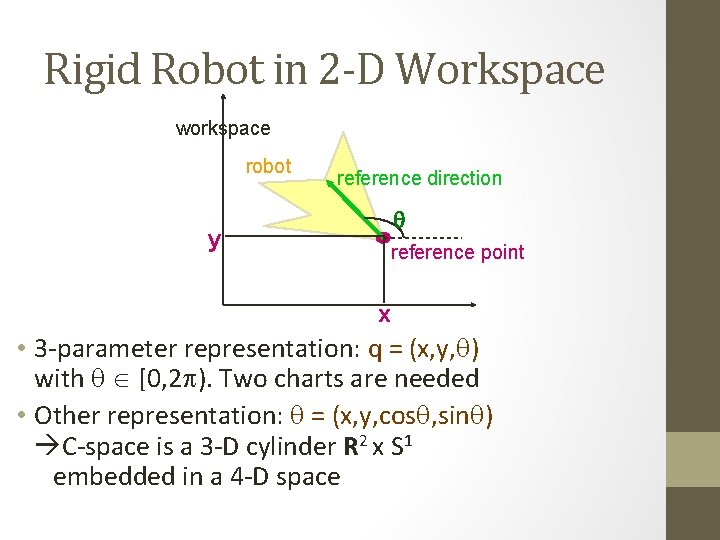
Rigid Robot in 2 -D Workspace workspace robot y reference direction q reference point x • 3 -parameter representation: q = (x, y, q) with q [0, 2 p). Two charts are needed • Other representation: q = (x, y, cosq, sinq) C-space is a 3 -D cylinder R 2 x S 1 embedded in a 4 -D space

Rigid Robot in 3 -D Workspace • q = (x, y, z, a, b, g) • Other representation: q = (x, y, z, r 11, r 12, …, r 33) where r 11, r 12, …, r 33 are the elements of rotation matrix R: r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 with: • ri 12+ri 22+ri 32 = 1 • ri 1 rj 1 + ri 2 r 2 j + ri 3 rj 3 = 0 • det(R) = +1

Rigid Robot in 3 -D Workspace • q = (x, y, z, a, b, g) The c-space is a 6 -D space (manifold) embedded • Other representation: q = (x, y, z, r in a 12 -D Cartesian space. It is denoted by 33) 11, r 12, …, r where r 11, r 12, …, r 33 are the elements of rotation matrix SE(3) =R: R 3 x. SO(3) r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 with: • ri 12+ri 22+ri 32 = 1 • ri 1 rj 1 + ri 2 r 2 j + ri 3 rj 3 = 0 • det(R) = +1

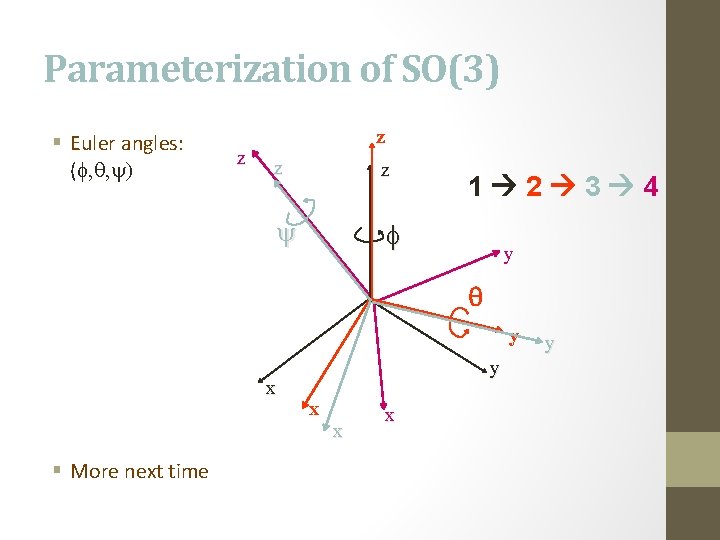
Parameterization of SO(3) § Euler angles: (f, q, y) z z y f 1 2 3 4 y q y x § More next time y x x x y

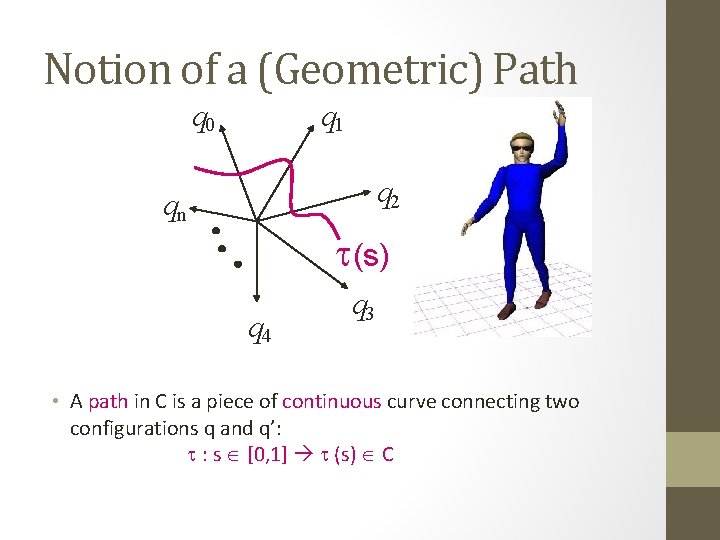
Notion of a (Geometric) Path q 0 q 1 q 2 qn t(s) q 4 q 3 • A path in C is a piece of continuous curve connecting two configurations q and q’: t : s [0, 1] t (s) C

Examples • A straight line segment linearly interpolating between a and b • t(s) = (1 -s) a + s b • What about interpolating orientations? • A polynomial with coeffients c 0, …, cn • t(s) = c 0 + c 1 s + … + cnsn • Piecewise polynomials • Piecewise linear • Splines (B-spline, hermite splines are popular) • Can be an arbitrary curve • Only limited by your imagination and representation capabilities

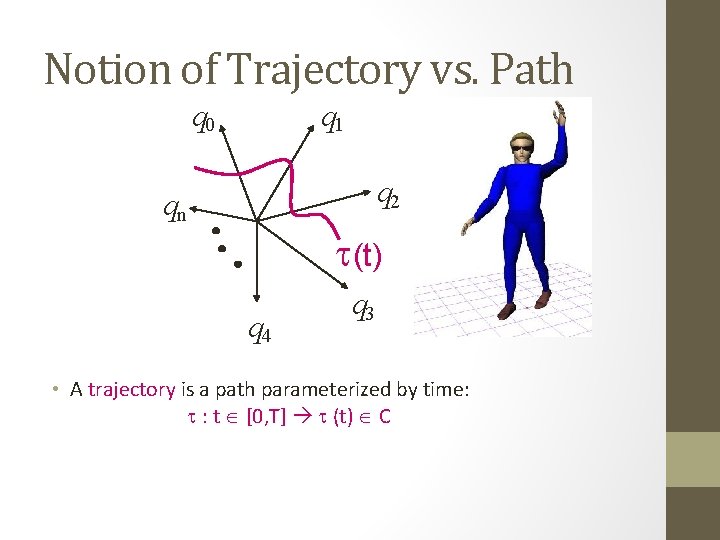
Notion of Trajectory vs. Path q 0 q 1 q 2 qn t(t) q 4 q 3 • A trajectory is a path parameterized by time: t [0, T] t (t) C

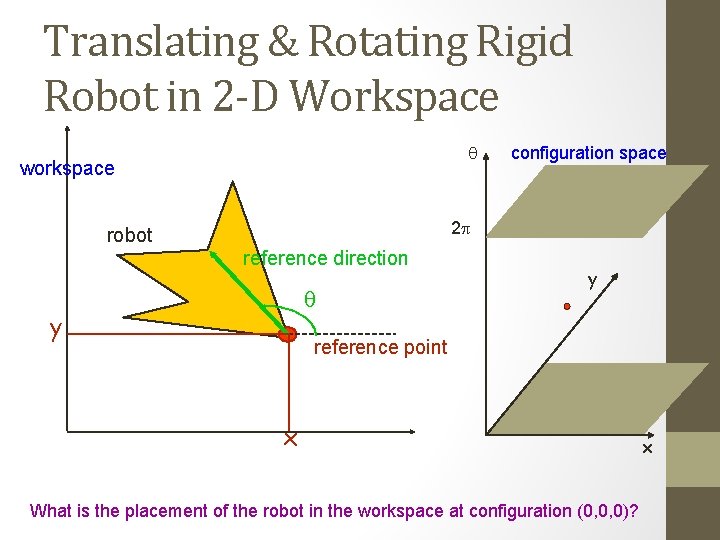
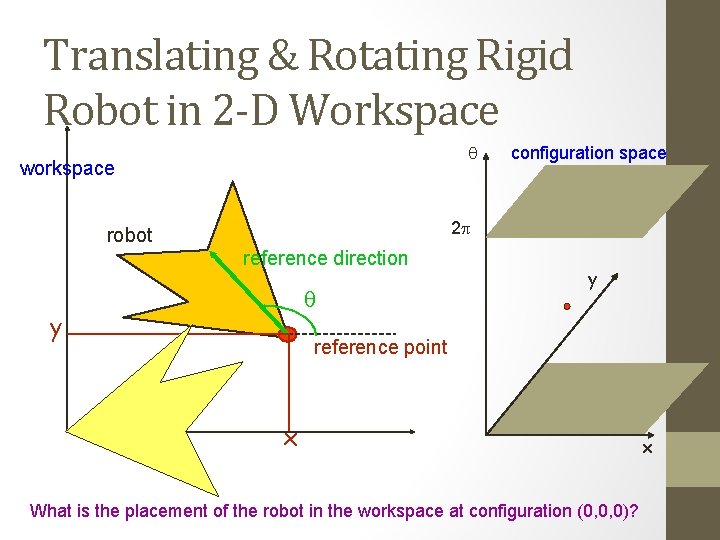
Translating & Rotating Rigid Robot in 2 -D Workspace q workspace configuration space 2 p robot reference direction q y y reference point x What is the placement of the robot in the workspace at configuration (0, 0, 0)? x

Translating & Rotating Rigid Robot in 2 -D Workspace q workspace configuration space 2 p robot reference direction q y y reference point x What is the placement of the robot in the workspace at configuration (0, 0, 0)? x

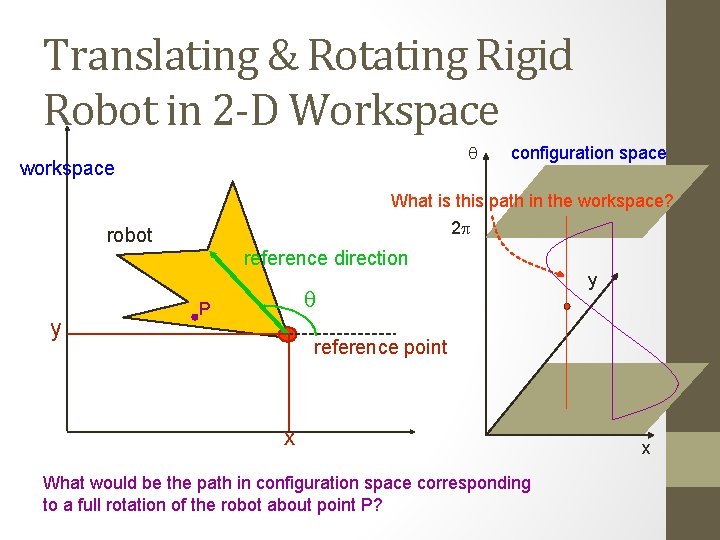
Translating & Rotating Rigid Robot in 2 -D Workspace q workspace configuration space What is this path in the workspace? 2 p robot reference direction y q P y reference point x What would be the path in configuration space corresponding to a full rotation of the robot about point P? x

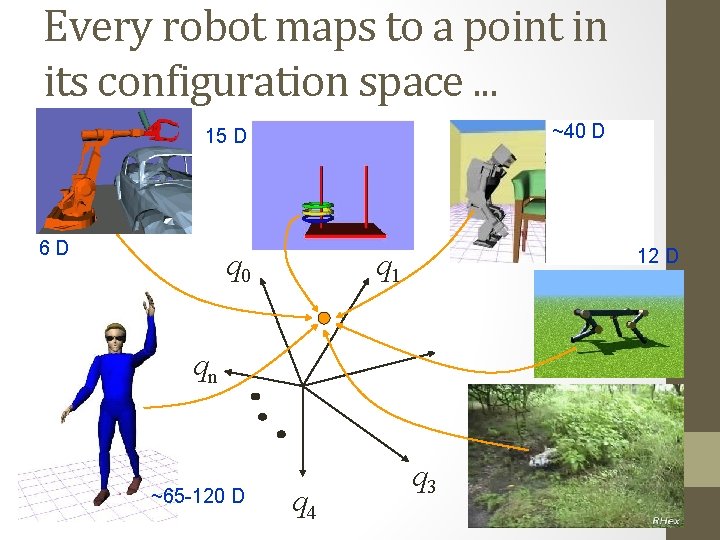
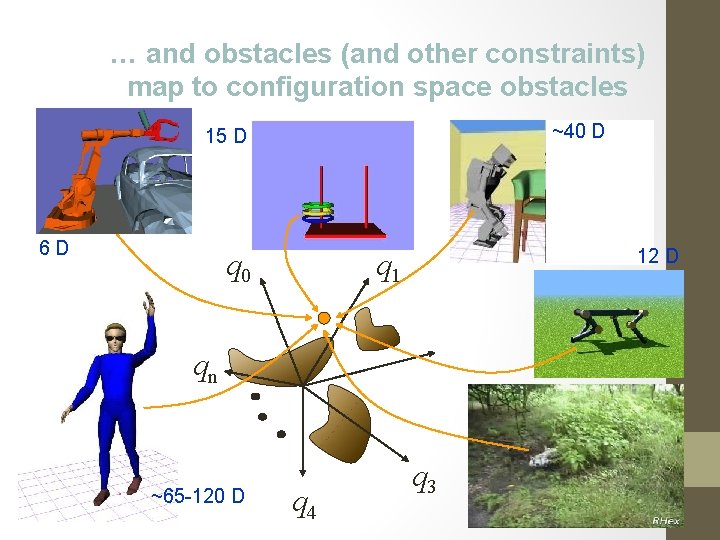
Every robot maps to a point in its configuration space. . . ~40 D 15 D 6 D q 0 12 D q 1 qn ~65 -120 D q 4 q 3

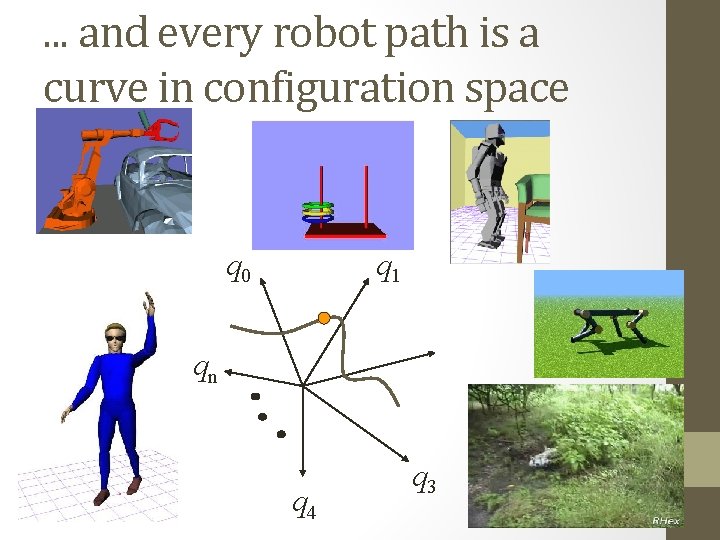
. . . and every robot path is a curve in configuration space q 0 q 1 qn q 4 q 3

… and obstacles (and other constraints) map to configuration space obstacles ~40 D 15 D 6 D q 0 12 D q 1 qn ~65 -120 D q 4 q 3

Obstacles in C-Space • A configuration q is collision-free, or free, if the robot placed at q has null intersection with the obstacles in the workspace • The free space F is the set of free configurations • A C-obstacle is the set of configurations where the robot collides with a given workspace obstacle • A configuration is semi-free if the robot at this configuration touches obstacles without overlap

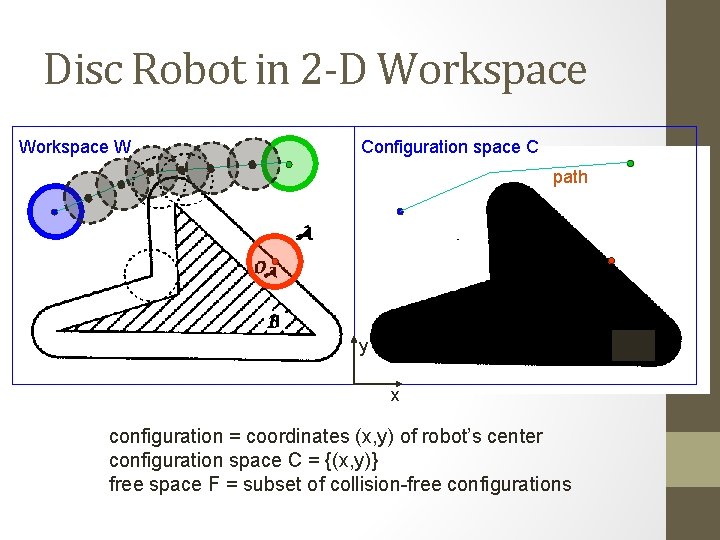
Disc Robot in 2 -D Workspace W Configuration space C path y x configuration = coordinates (x, y) of robot’s center configuration space C = {(x, y)} free space F = subset of collision-free configurations

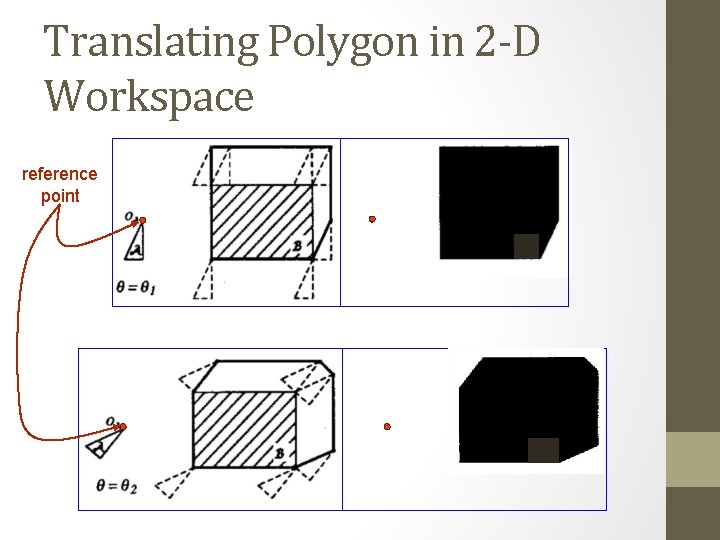
Translating Polygon in 2 -D Workspace reference point

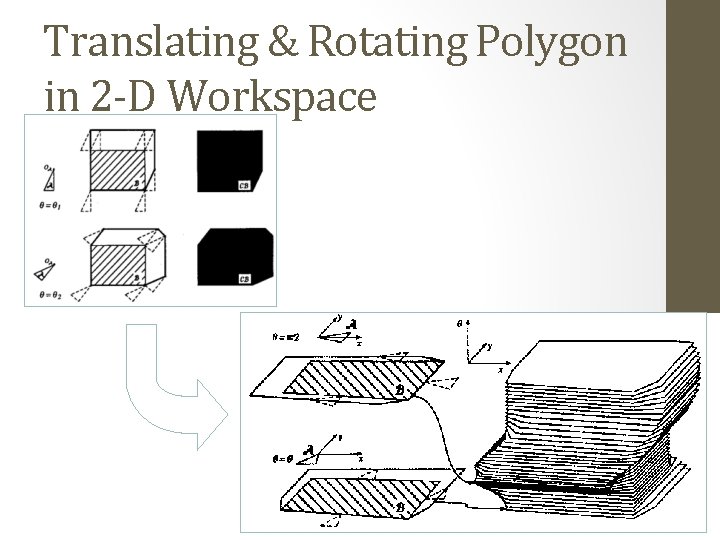
Translating & Rotating Polygon in 2 -D Workspace

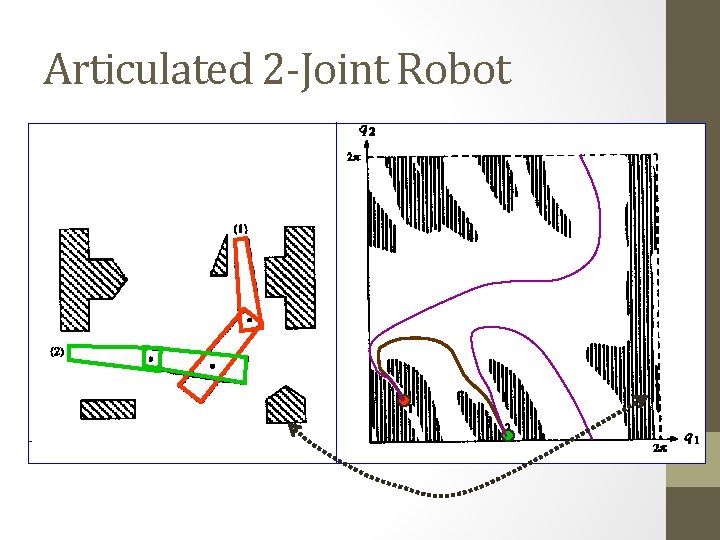
Articulated 2 -Joint Robot

Some constraints can’t be modeled as C-Space obstacles • Differential constraints: smoothness, finite curvature, drift, etc… • Global constraints: finite length, power consumption, etc…

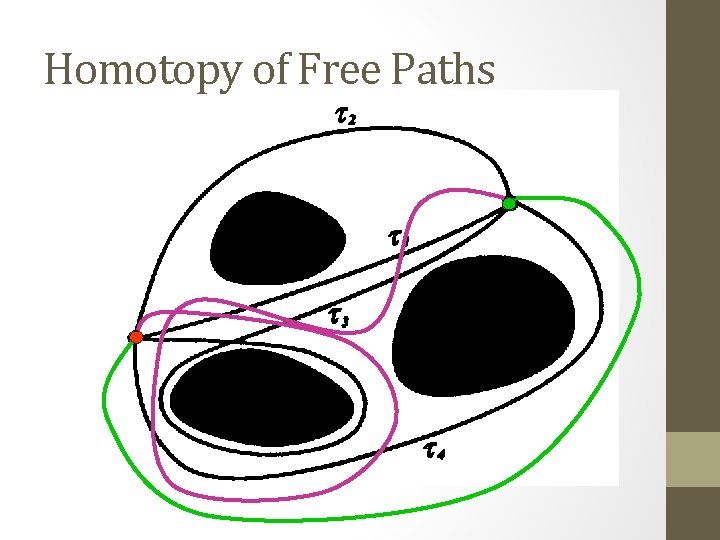
Homotopic Paths • Two paths with the same endpoints are homotopic if one can be continuously deformed into the other • Rx. S 1 example: q t 3 t 1 • t 1 and t 2 are homotopic • t 1 and t 3 are not homotopic • In this example, infinity of homotopy classes t 2 q’

Connectedness of C-Space • C is connected if every two configurations can be connected by a path • C is simply-connected if any two paths connecting the same endpoints are homotopic Examples: R 2 or R 3 • Otherwise C is multiply-connected Examples: S 1 and SO(3) are multiply-connected: - In S 1, infinity of homotopy classes - In SO(3), only two homotopy classes

Homotopy of Free Paths

Recap • Configuration space: • Tool to map a robot in a 2 -D or 3 -D workspace into a point in n-D space • Topological spaces • Mapping obstacles into C-space

Readings • Principles Ch. 3. 5 -3. 8, Appendix E

Notions of Continuity • Path continuity (geometric, or C 0) • For all s, d(t(s), t(s’)) -> 0 as s’->s • Trajectory continuity (geometric, or C 0) • For all t, d(t(t), t(t’)) -> 0 as t’->t • Higher order continuity • C 1: For all t, t’(t) is well defined • C 2: For all t, t’’(t) is well defined • …

Metric in Configuration Space A metric or distance function d in C is a map d: (q 1, q 2) C 2 d(q 1, q 2) > 0 such that: • d(q 1, q 2) = 0 if and only if q 1 = q 2 • d(q 1, q 2) = d (q 2, q 1) • d(q 1, q 2) < d(q 1, q 3) + d(q 3, q 2)

Metric in Configuration Space Example: • Robot A and point x of A • x(q): location of x in the workspace when A is at configuration q • A distance d in C is defined by: d(q, q’) = maxx A ||x(q)-x(q’)|| where ||a - b|| denotes the Euclidean distance between points a and b in the workspace

Specific Examples in R 2 x S 1 § q = (x, y, q), q’ = (x’, y’, q’) with q, q’ [0, 2 p) § a = min{|q-q’| , 2 p-|q-q’|} q a § d(q, q’) = sqrt[(x-x’)2 + (y-y’)2 + a 2] § d(q, q’) = sqrt[(x-x’)2 + (y-y’)2 + (ar)2] where r is the maximal distance between the reference point and a robot point q’