CONFIDENCE INTERVALS A confidence interval is an interval

CONFIDENCE INTERVALS A confidence interval is an interval in which we are certain to a given probability of the mean lying in that interval. For example if a 95% confidence interval is given, then 95% of the intervals would contain a true mean. We used z-interval with normal distribution or CLT where the standard deviation of the population was known. From a sample we usually don’t know anything about the population. So we use the t -distribution in theses situations and t-interval. use sample mean and unbiased estimate of standard deviation. As n increases, t - distribution becomes closer to normal distribution.

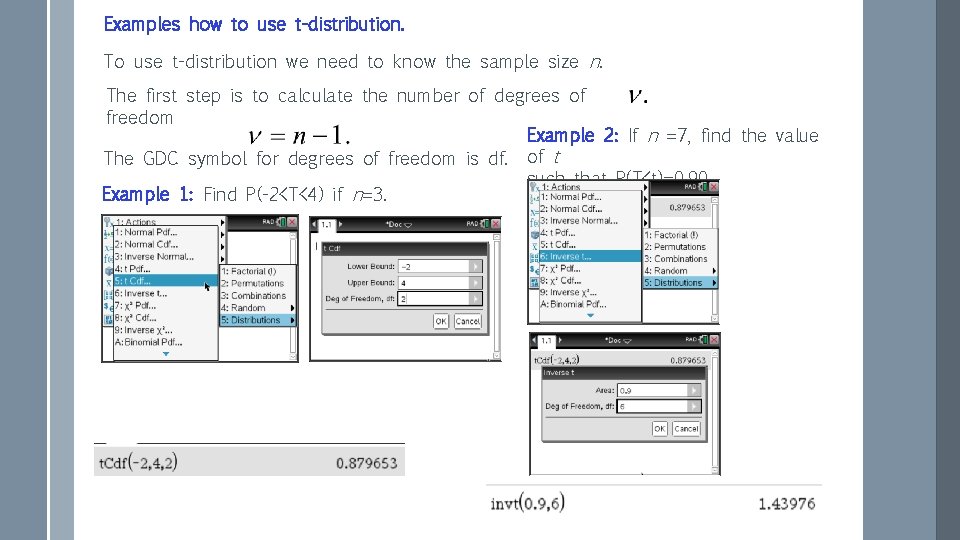
Examples how to use t-distribution. To use t-distribution we need to know the sample size n. The first step is to calculate the number of degrees of freedom Example 2: If n =7, find the value The GDC symbol for degrees of freedom is df. of t such that P(T<t)=0. 90. Example 1: Find P(-2<T<4) if n=3.

Confidence intervals Again if the standard deviation of the population is NOT known, and has to be estimated from the sample, then the distribution is altered to that of a Student-t distribution. Example 1 https: //osc-ib. com/ib-video-revision/confidence-interval Example 2 parts a and b only, without hypothesis testing yet. https: //osc-ib. com/ib-video-revision/confidence-intervals

Example 3 (given confidence interval, find confidence level). https: //osc-ib. com/ib-video-revision/confidence-levels

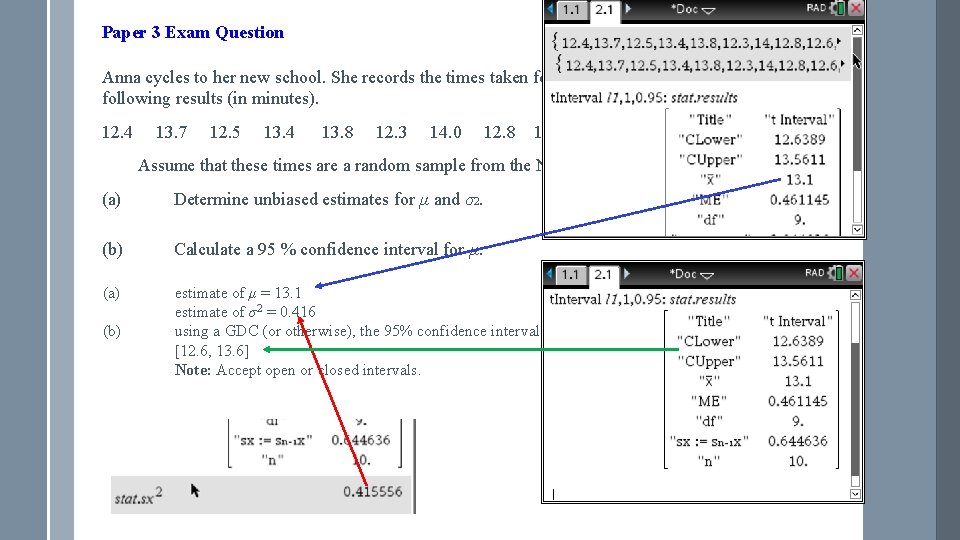
Paper 3 Exam Question Anna cycles to her new school. She records the times taken for the first ten days with the following results (in minutes). 12. 4 13. 7 12. 5 13. 4 13. 8 12. 3 14. 0 12. 8 12. 6 13. 5 Assume that these times are a random sample from the N(µ, σ2) distribution. (a) Determine unbiased estimates for µ and σ2. (2) (b) Calculate a 95 % confidence interval for µ. (3) (a) (b) estimate of μ = 13. 1 estimate of σ2 = 0. 416 using a GDC (or otherwise), the 95% confidence interval is [12. 6, 13. 6] Note: Accept open or closed intervals. A 1 (M 1) A 1 A 1