Confidence Intervals 1 a100 Confidence Intervals 1 Mean
















![In the last example 1. a = P[ type I error] = p(0) + In the last example 1. a = P[ type I error] = p(0) +](https://slidetodoc.com/presentation_image_h2/816a808887f2b3378be9e908afa3969a/image-19.jpg)

![Comments: 1. You can control a = P[ type I error] and b = Comments: 1. You can control a = P[ type I error] and b =](https://slidetodoc.com/presentation_image_h2/816a808887f2b3378be9e908afa3969a/image-24.jpg)
















- Slides: 48

Confidence Intervals

(1 – a)100 % Confidence Intervals 1. Mean, m, of a Normal population (s known). 2. Mean, m, of a Normal population (s unknown). 3. Variance, s 2, of a Normal population.

4. Standard deviation, s, of a Normal population. 5. Success-failure (Bernoulli) probability, p. 6. General parameter, q.

Hypothesis Testing An important area of statistical inference

Definition Hypothesis (H) – Statement about the parameters of the population • In hypothesis testing there are two hypotheses of interest. – The null hypothesis (H 0) – The alternative hypothesis (HA)

Either – null hypothesis (H 0) is true or – the alternative hypothesis (HA) is true. But not both We say that are mutually exclusive and exhaustive.

One has to make a decision – to either to accept null hypothesis (equivalent to rejecting HA) or – to reject null hypothesis (equivalent to accepting HA)

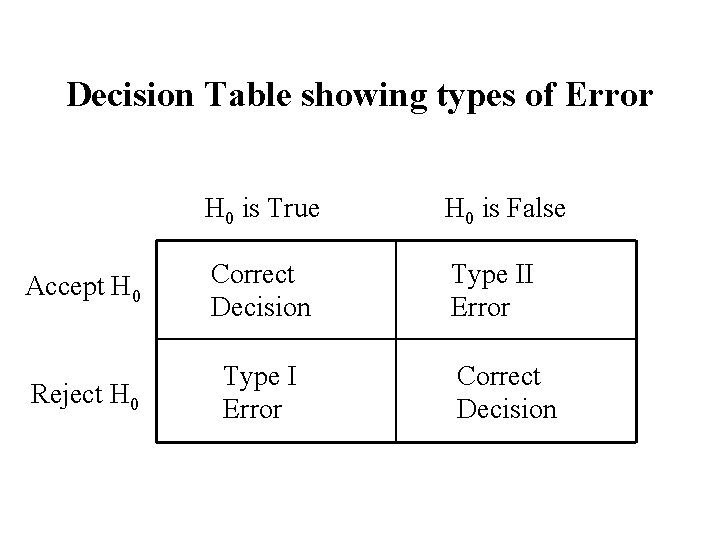
There are two possible errors that can be made. 1. Rejecting the null hypothesis when it is true. (type I error) 2. accepting the null hypothesis when it is false (type II error)

An analogy – a jury trial The two possible decisions are – Declare the accused innocent. – Declare the accused guilty.

The null hypothesis (H 0) – the accused is innocent The alternative hypothesis (HA) – the accused is guilty

The two possible errors that can be made: – Declaring an innocent person guilty. (type I error) – Declaring a guilty person innocent. (type II error) Note: in this case one type of error may be considered more serious

Decision Table showing types of Error H 0 is True H 0 is False Accept H 0 Correct Decision Type II Error Reject H 0 Type I Error Correct Decision

To define a statistical Test we 1. Choose a statistic (called the test statistic) 2. Divide the range of possible values for the test statistic into two parts • The Acceptance Region • The Critical Region

To perform a statistical Test we 1. Collect the data. 2. Compute the value of the test statistic. 3. Make the Decision: • If the value of the test statistic is in the Acceptance Region we decide to accept H 0. • If the value of the test statistic is in the Critical Region we decide to reject H 0.

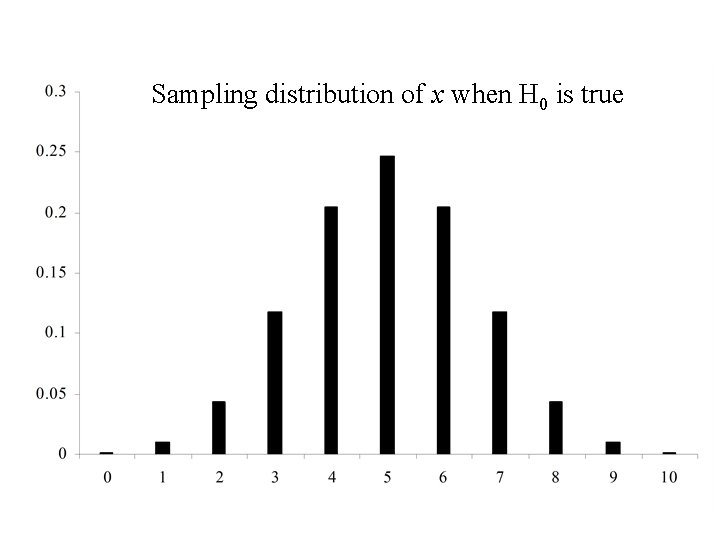
Example We are interested in determining if a coin is fair. i. e. H 0 : p = probability of tossing a head = ½. To test this we will toss the coin n = 10 times. The test statistic is x = the number of heads. This statistic will have a binomial distribution with p = ½ and n = 10 if the null hypothesis is true.

Sampling distribution of x when H 0 is true

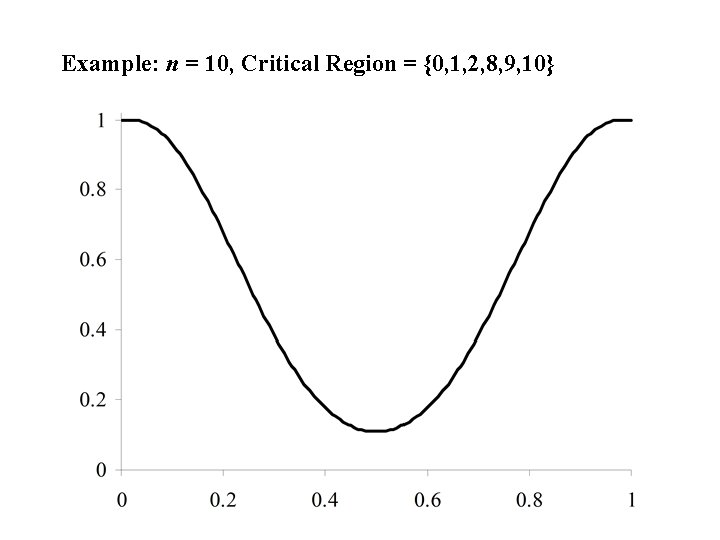
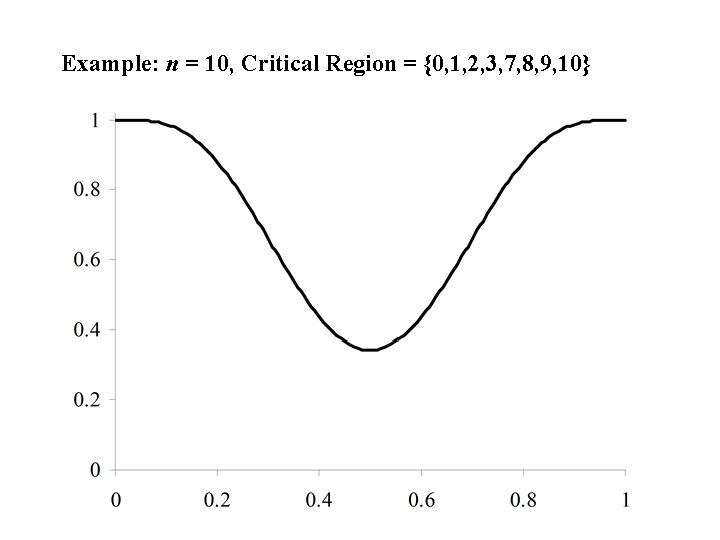
Note We would expect the test statistic x to be around 5 if H 0 : p = ½ is true. Acceptance Region = {3, 4, 5, 6, 7}. Critical Region = {0, 1, 2, 8, 9, 10}. The reason for the choice of the Acceptance region: Contains the values that we would expect for x if the null hypothesis is true.

Definitions: For any statistical testing procedure define 1. a = P[Rejecting the null hypothesis when it is true] = P[ type I error] 2. b = P[accepting the null hypothesis when it is false] = P[ type II error]
![In the last example 1 a P type I error p0 In the last example 1. a = P[ type I error] = p(0) +](https://slidetodoc.com/presentation_image_h2/816a808887f2b3378be9e908afa3969a/image-19.jpg)
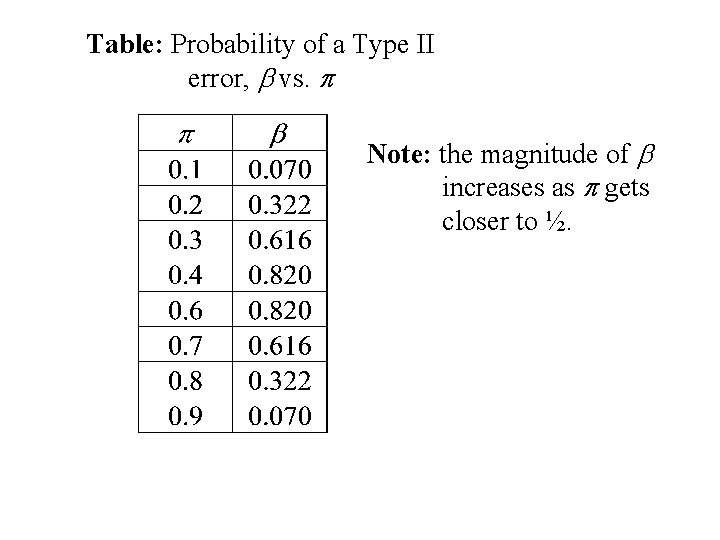
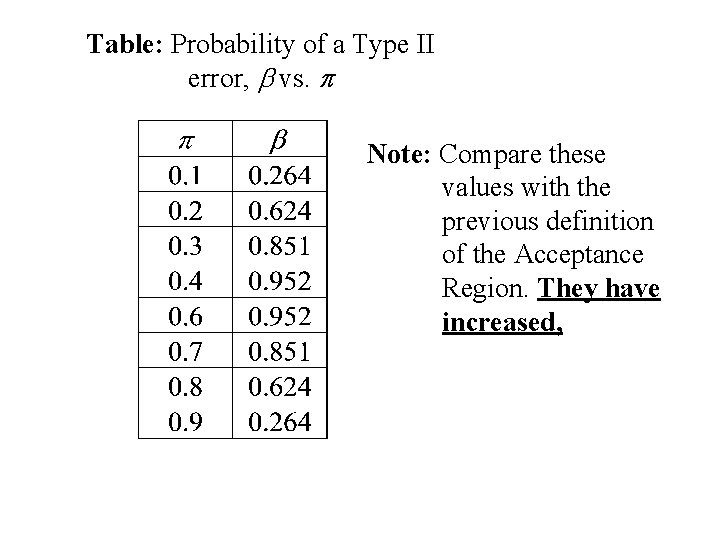
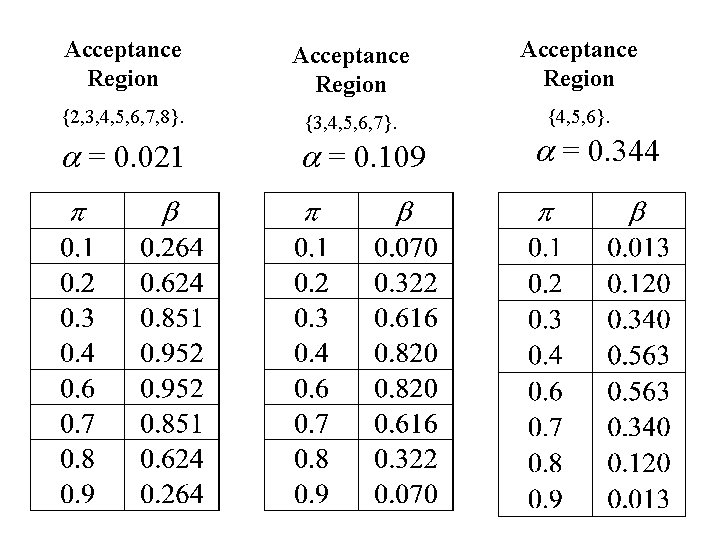
In the last example 1. a = P[ type I error] = p(0) + p(1) + p(2) + p(8) + p(9) + p(10) = 0. 109, where p(x) are binomial probabilities with p = ½ and n = 10. 2. b = P[ type II error] = p(3) + p(4) + p(5) + p(6) + p(7), where p(x) are binomial probabilities with p (not equal to ½) and n = 10. Note: these will depend on the value of p.

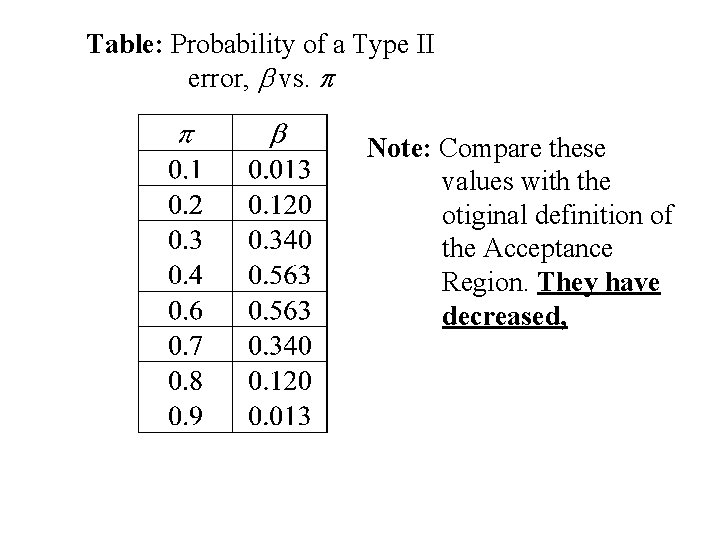
Table: Probability of a Type II error, b vs. p Note: the magnitude of b increases as p gets closer to ½.

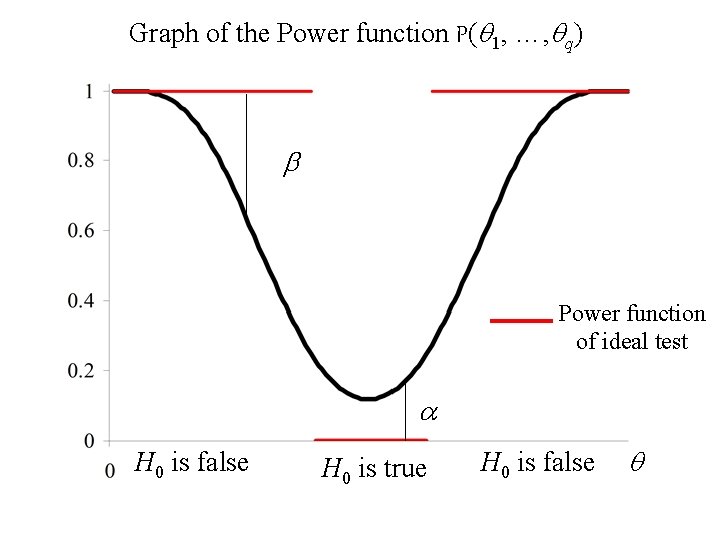
The Power function of a Statistical Test Definition: The Power Function, P(q 1, …, qq) of a statistical test is defined as follows: P(q 1, …, qq) = P[ test rejects H 0] Note: if H 0 is true P(q 1, …, qq) = P[rejects H 0 ] = P[Type I error] = a. if H 0 is false P(q 1, …, qq) = P[rejects H 0 ] = 1 - P[Type II error] = 1 - b.

Graph of the Power function P(q 1, …, qq) b Power function of ideal test a H 0 is false H 0 is true H 0 is false q

Example: n = 10, Critical Region = {0, 1, 2, 8, 9, 10}
![Comments 1 You can control a P type I error and b Comments: 1. You can control a = P[ type I error] and b =](https://slidetodoc.com/presentation_image_h2/816a808887f2b3378be9e908afa3969a/image-24.jpg)
Comments: 1. You can control a = P[ type I error] and b = P[ type II error] by widening or narrowing the acceptance region. . 2. Widening the acceptance region decreases a = P[ type I error] but increases b = P[ type II error]. 3. Narrowing the acceptance region increases a = P[ type I error] but decreases b = P[ type II error].

Example – Widening the Acceptance Region 1. Suppose the Acceptance Region includes in addition to its previous values 2 and 8 then a = P[ type I error] = p(0) + p(1) + p(9) + p(10) = 0. 021, where again p(x) are binomial probabilities with p = ½ and n = 10. 2. b = P[ type II error] = p(2) + p(3) + p(4) + p(5) + p(6) + p(7) + p(8). Tabled values of are given on the next page.

Table: Probability of a Type II error, b vs. p Note: Compare these values with the previous definition of the Acceptance Region. They have increased,

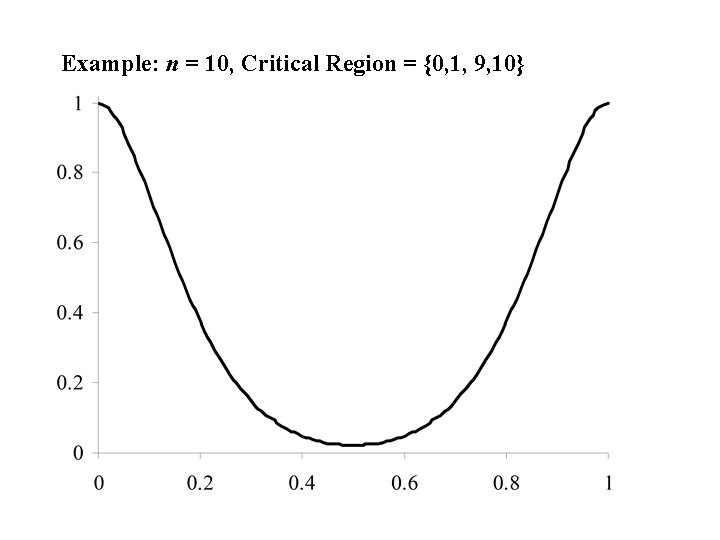
Example: n = 10, Critical Region = {0, 1, 9, 10}

Example – Narrowing the Acceptance Region 1. Suppose the original Acceptance Region excludes the values 3 and 7. That is the Acceptance Region is {4, 5, 6}. Then a = P[ type I error] = p(0) + p(1) + p(2) + p(3) + p(7) + p(8) +p(9) + p(10) = 0. 344. 2. b = P[ type II error] = p(4) + p(5) + p(6). Tabled values of are given on the next page.

Table: Probability of a Type II error, b vs. p Note: Compare these values with the otiginal definition of the Acceptance Region. They have decreased,

Example: n = 10, Critical Region = {0, 1, 2, 3, 7, 8, 9, 10}

Acceptance Region {2, 3, 4, 5, 6, 7, 8}. {3, 4, 5, 6, 7}. {4, 5, 6}. a = 0. 021 a = 0. 109 a = 0. 344

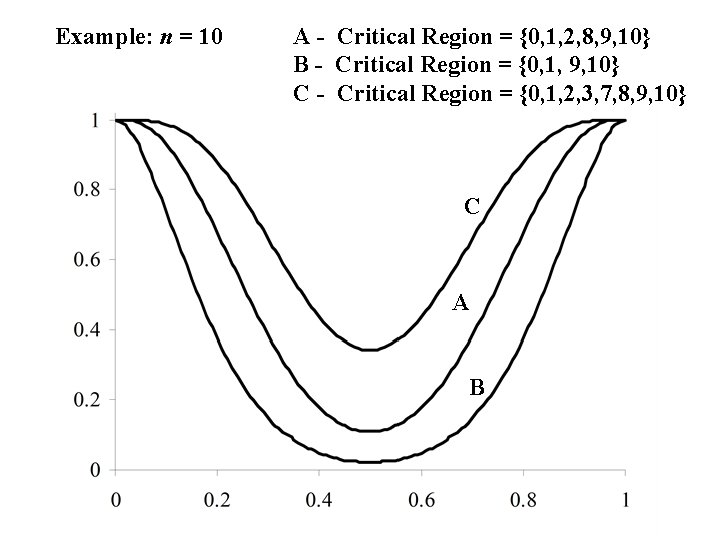
Example: n = 10 A - Critical Region = {0, 1, 2, 8, 9, 10} B - Critical Region = {0, 1, 9, 10} C - Critical Region = {0, 1, 2, 3, 7, 8, 9, 10} C A B

The Approach in Statistical Testing is: • Set up the Acceptance Region so that a is close to some predetermine value (the usual values are 0. 05 or 0. 01) • The predetermine value of a (0. 05 or 0. 01) is called the significance level of the test. • The significance level (size) of the test is a = P[test makes a type I error]

The z-test for the Mean of a Normal Population We want to test, m, denote the mean of a normal population

The t distribution Estimating m, the mean of a Normal population (s 2 unknown) Let x 1, … , xn denote a sample from the normal distribution with mean m and variance s 2. Both m and s 2 are unknown Recall Also

Situation Let x 1, … , xn denote a sample from the normal distribution with mean m and variance s 2. Both m is unknown and s 2 is known We want to test – H 0: m = m 0 (some specified value of m) Against – H A:

The Data • Let x 1, x 2, x 3 , … , xn denote a sample from a normal population with mean m and standard deviation s. • Let • we want to test if the mean, m, is equal to some given value m 0. • Obviously if the sample mean is close to m 0 the Null Hypothesis should be accepted otherwise the null Hypothesis should be rejected.

The Test Statistic • To decide to accept or reject the Null Hypothesis (H 0) we will use the test statistic • If H 0 is true we should expect the test statistic z to be close to zero. • If H 0 is true we should expect the test statistic z to have a standard normal distribution. • If HA is true we should expect the test statistic z to be different from zero.

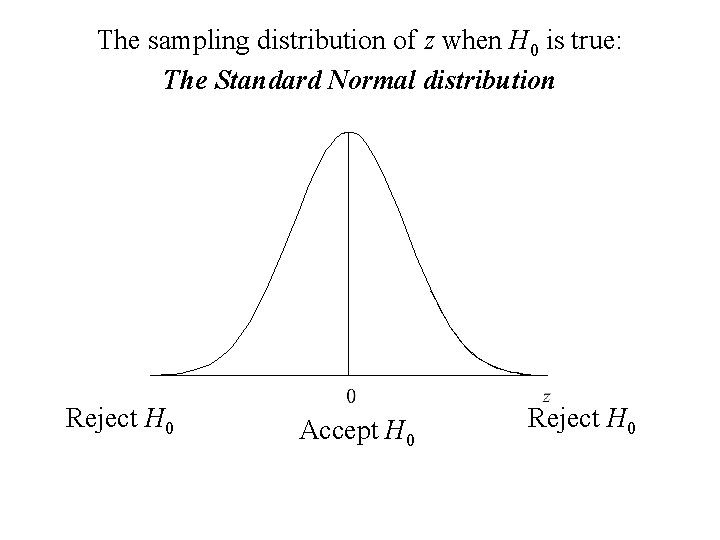
The sampling distribution of z when H 0 is true: The Standard Normal distribution Reject H 0 Accept H 0 Reject H 0

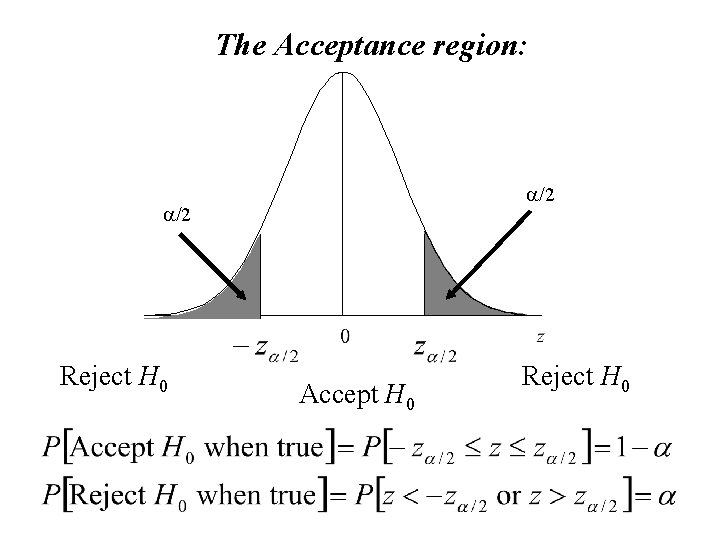
The Acceptance region: a/2 Reject H 0 Accept H 0 Reject H 0

• Acceptance Region – Accept H 0 if: • Critical Region – Reject H 0 if: • With this Choice

Summary To Test for a binomial probability m H 0: m = m 0 (some specified value of m) Against H A: 1. Decide on a = P[Type I Error] = the significance level of the test (usual choices 0. 05 or 0. 01)

2. Collect the data 3. Compute the test statistic 4. Make the Decision • Accept H 0 if: • Reject H 0 if:

Example A manufacturer Glucosamine capsules claims that each capsule contains on the average: • 500 mg of glucosamine To test this claim n = 40 capsules were selected and amount of glucosamine (X) measured in each capsule. Summary statistics:

We want to test: Manufacturers claim is correct against Manufacturers claim is not correct

The Test Statistic

The Critical Region and Acceptance Region Using a = 0. 05 za/2 = z 0. 025 = 1. 960 We accept H 0 if -1. 960 ≤ z ≤ 1. 960 reject H 0 if z < -1. 960 or z > 1. 960

The Decision Since z= -2. 75 < -1. 960 We reject H 0 Conclude: the manufacturer's claim is incorrect:
 Emt a100
Emt a100 How to add 95 confidence intervals in excel
How to add 95 confidence intervals in excel Chapter 19 confidence intervals for proportions
Chapter 19 confidence intervals for proportions Confidence interval ti 84
Confidence interval ti 84 96 confidence interval z score
96 confidence interval z score Confidence interval variance formula
Confidence interval variance formula Confidence intervals excel
Confidence intervals excel Confidence intervals minitab
Confidence intervals minitab Reporting confidence intervals
Reporting confidence intervals Chapter 18 confidence intervals for proportions
Chapter 18 confidence intervals for proportions Chapter 19 confidence intervals for proportions
Chapter 19 confidence intervals for proportions One sample z interval formula
One sample z interval formula Preparing to estimate a population proportion
Preparing to estimate a population proportion Significance level and confidence level
Significance level and confidence level Confidence interval vs confidence level
Confidence interval vs confidence level Zinterval
Zinterval Confidence interval for mean
Confidence interval for mean Confidence interval formula
Confidence interval formula Confidence interval for population mean
Confidence interval for population mean What does mean mean
What does mean mean Sampling distribution of the mean
Sampling distribution of the mean Mean deviation
Mean deviation How to find best point estimate
How to find best point estimate Say, mean, matter
Say, mean, matter Difference between sample mean and population mean
Difference between sample mean and population mean Mean of the sampling distribution of the sample mean
Mean of the sampling distribution of the sample mean Mean average deviation formula
Mean average deviation formula Error intervals
Error intervals Greek alphabet alpha beta gamma delta
Greek alphabet alpha beta gamma delta Short pr intervals
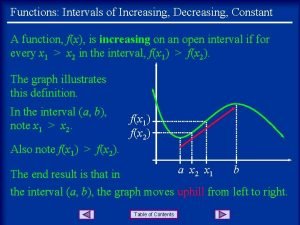
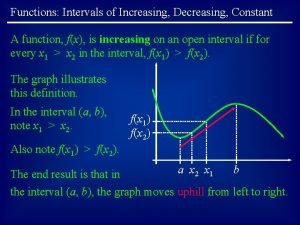
Short pr intervals Increasing and decreasing intervals
Increasing and decreasing intervals Monotone intervals
Monotone intervals Error intervals
Error intervals Chapter 20 more about tests and intervals
Chapter 20 more about tests and intervals Error intervals significant figures
Error intervals significant figures Class intervals histogram
Class intervals histogram Musical form of pamulinawen
Musical form of pamulinawen Normal.ecg intervals
Normal.ecg intervals Statistical intervals for a single sample
Statistical intervals for a single sample Error intervals gcse questions
Error intervals gcse questions Interval of increase and decrease parabola
Interval of increase and decrease parabola Removable and non removable discontinuities
Removable and non removable discontinuities How to find increasing and decreasing intervals on a graph
How to find increasing and decreasing intervals on a graph Increasing function
Increasing function 24 hour clock time
24 hour clock time Confidence interval 68 95 99
Confidence interval 68 95 99 Treat with confidence
Treat with confidence Mean difference formula
Mean difference formula Interval notation for infinity
Interval notation for infinity