Conductors and Dielectrics Conductors Current current density drift

Conductors and Dielectrics • Conductors – – – Current, current density, drift velocity, continuity Energy bands in materials Mobility, micro/macro Ohm’s Law Boundary conditions on conductors Methods of Images • Dielectrics – – Polarization, displacement, electric field Permittivity, susceptibility, relative permittivity Dielectrics research Boundary conditions on dielectrics

Conductors and Dielectrics • Polarization – Static alignment of charge in material – Charge aligns when voltage applied, moves no further – Charge proportional to voltage • Conduction – Continuous motion of charge through material – Enters one side, exits another – Current proportional to voltage • Real-world materials – Plastics, ceramics, glasses -> dielectrics (maybe some conductivity) – Metals -> conductors, semiconductors, superconductors – Cement, Biosystems -> Both (water high dielectric, salt conductivity)

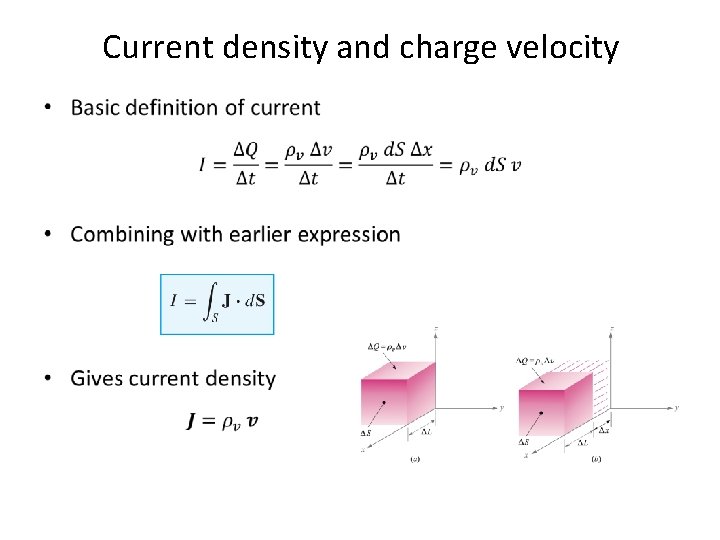
Current and current density • Basic definition of current C/s = Amps • Basic current density (J perp. surface) • Vector current density n

Current density and charge velocity •

Charge and current continuity • Current leaving any closed surface is time rate of change of charge within that surface • Using divergence theorem on left • Taking time derivative inside integral Qi(t) • Equating integrands

Example – charge and current continuity • ^^ Why is current increasing ? <<Some central repulsive force!

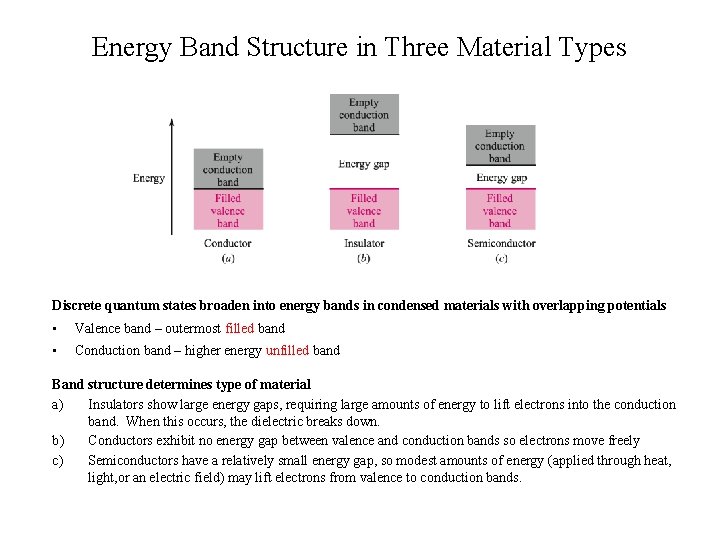
Energy Band Structure in Three Material Types Discrete quantum states broaden into energy bands in condensed materials with overlapping potentials • Valence band – outermost filled band • Conduction band – higher energy unfilled band Band structure determines type of material a) Insulators show large energy gaps, requiring large amounts of energy to lift electrons into the conduction band. When this occurs, the dielectric breaks down. b) Conductors exhibit no energy gap between valence and conduction bands so electrons move freely c) Semiconductors have a relatively small energy gap, so modest amounts of energy (applied through heat, light, or an electric field) may lift electrons from valence to conduction bands.

Ohm’s Law (microscopic form) Free electrons are accelerated by an electric field. The applied force on an electron of charge Q = -e is But in reality the electrons are constantly bumping into things (like a terminal velocity) so they attain an equilibrium or drift velocity: where e is the electron mobility, expressed in units of m 2/V-s. The drift velocity is used in the current density through: So Ohm’s Law in point form (material property) With the conductivity given as: S/m (electrons) S/m (electrons/holes)

Ohm’s Law (macroscopic form) •

Ohm’s Law example 1 •

Ohm’s Law example 2 •

Boundary conditions for conductors •

Boundary Condition for Tangential Electric Field E Over the rectangular integration path, we use or To find: These become negligible as h approaches zero. dielectric Therefore n More formally: conductor

Boundary Condition for the Normal Displacement D Gauss’ Law is applied to the cylindrical surface shown below: This reduces to: dielectric as h approaches zero Therefore n More formally: s conductor

Summary Tangential E is zero At the surface: Normal D is equal to the surface charge density

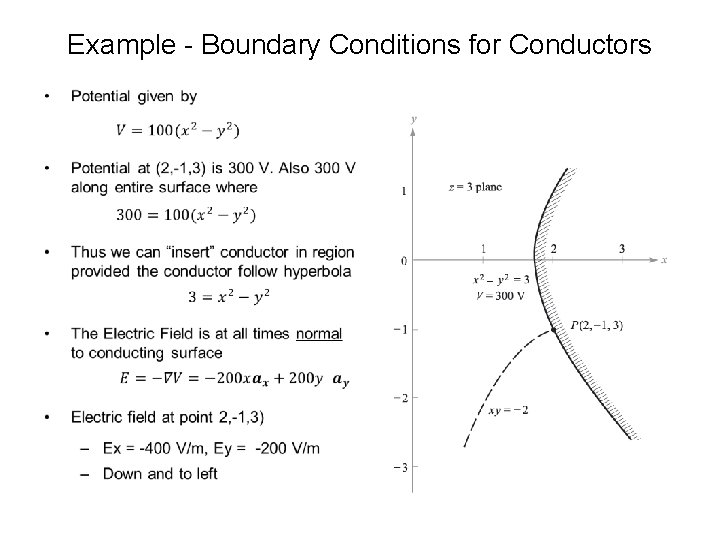
Example - Boundary Conditions for Conductors •

Example – Streamlines of Electric Field •

Boundary condition example (from my phone)* * www. mathstudio. net

Method of Images Theorem of Uniqueness states that if we are given a configuration of charges and boundary conditions, there will exist only one potential and electric field solution. In the electric dipole, the surface along the plane of symmetry is an equipotential with V = 0. The same is true if a grounded conducting plane is located there. So the boundary conditions and charges are identical in the upper half spaces of both configurations (not in the lower half). In effect, the positive point charge images across the conducting plane, allowing the conductor to be replaced by the image. The field and potential distribution in the upper half space is now found much more easily!

Forms of Image Charges Each charge in a given configuration will have its own image

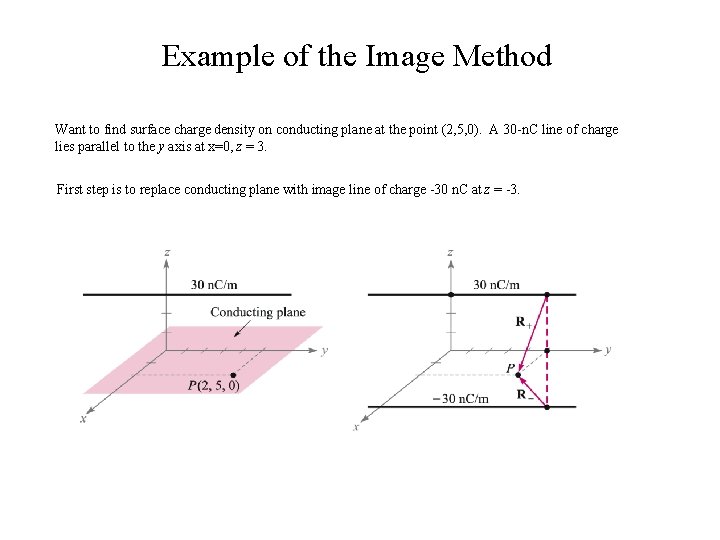
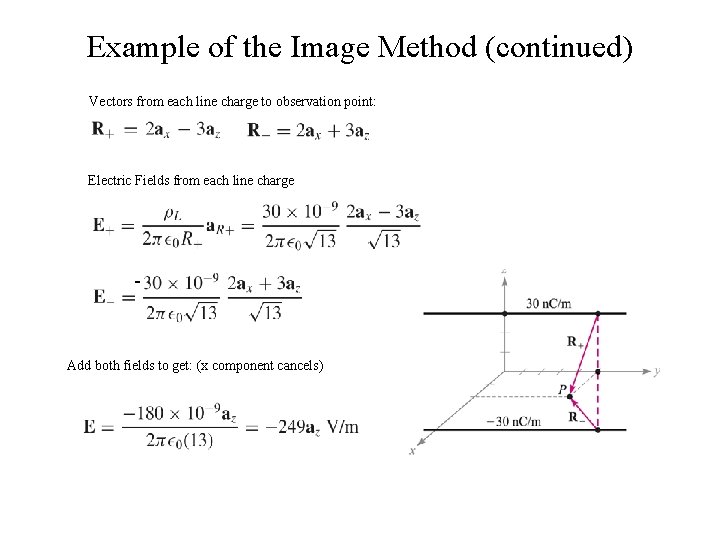
Example of the Image Method Want to find surface charge density on conducting plane at the point (2, 5, 0). A 30 -n. C line of charge lies parallel to the y axis at x=0, z = 3. First step is to replace conducting plane with image line of charge -30 n. C at z = -3.

Example of the Image Method (continued) Vectors from each line charge to observation point: Electric Fields from each line charge - Add both fields to get: (x component cancels)

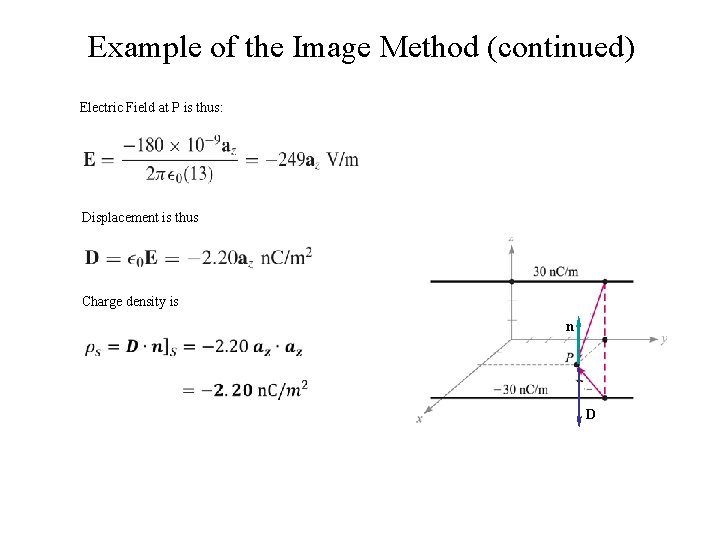
Example of the Image Method (continued) Electric Field at P is thus: Displacement is thus Charge density is n D

Image Method using Potentials •

Image Method using Potentials (cont) •

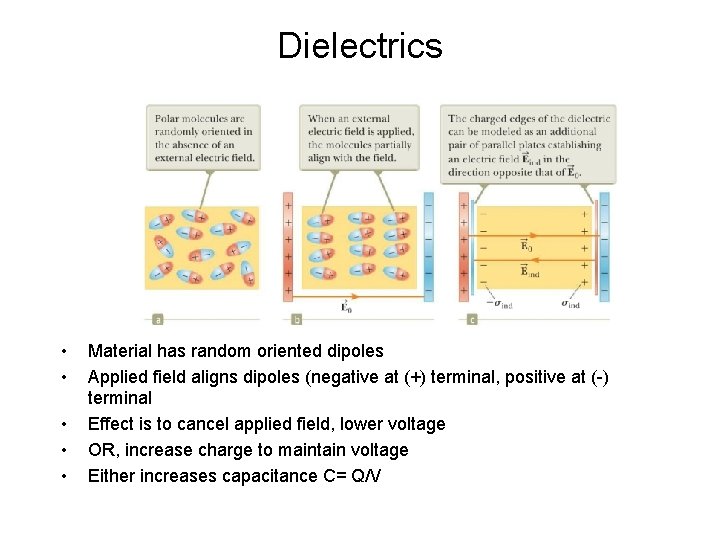
Dielectrics • • • Material has random oriented dipoles Applied field aligns dipoles (negative at (+) terminal, positive at (-) terminal Effect is to cancel applied field, lower voltage OR, increase charge to maintain voltage Either increases capacitance C= Q/V

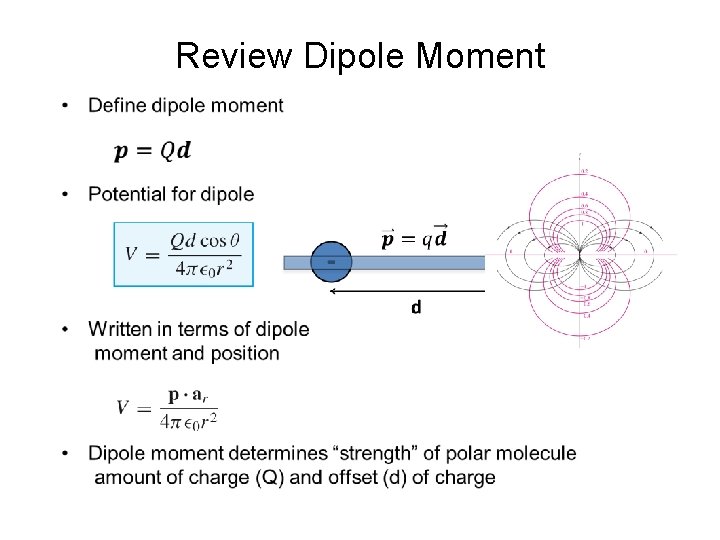
Review Dipole Moment •

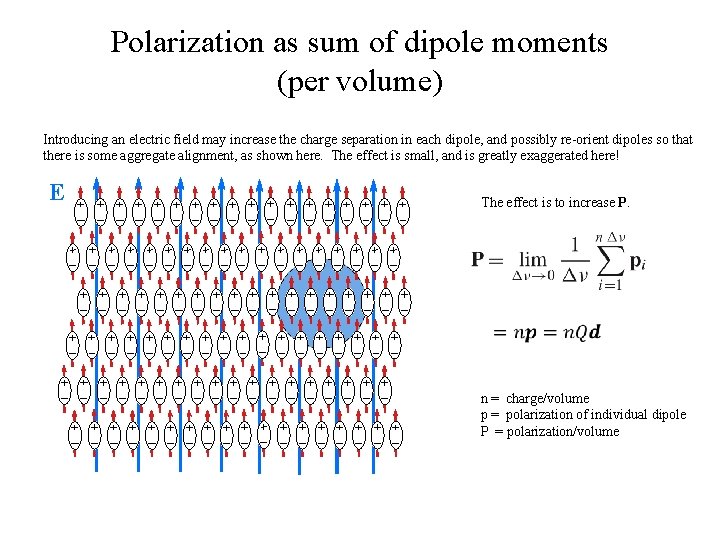
Polarization as sum of dipole moments (per volume) Introducing an electric field may increase the charge separation in each dipole, and possibly re-orient dipoles so that there is some aggregate alignment, as shown here. The effect is small, and is greatly exaggerated here! E The effect is to increase P. n = charge/volume p = polarization of individual dipole P = polarization/volume

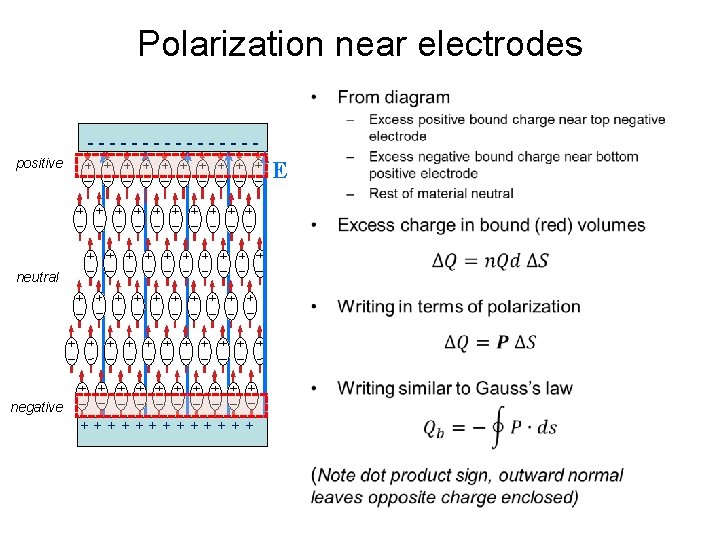
Polarization near electrodes • --------positive E neutral negative +++++++

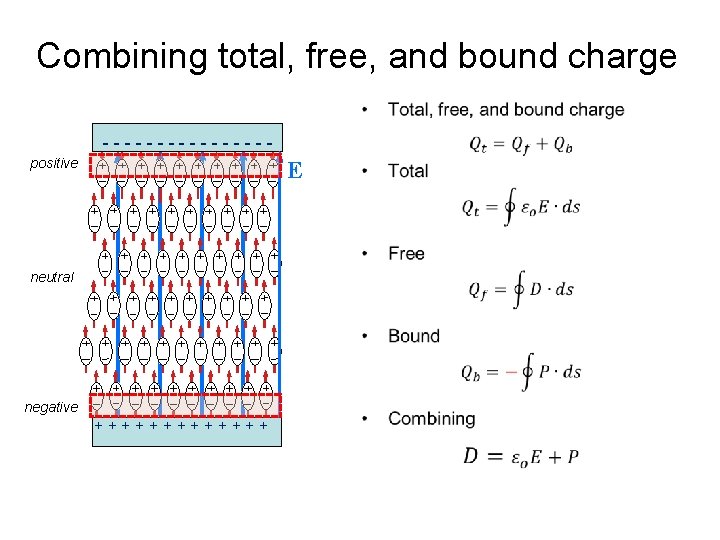
Combining total, free, and bound charge • --------positive E neutral negative +++++++

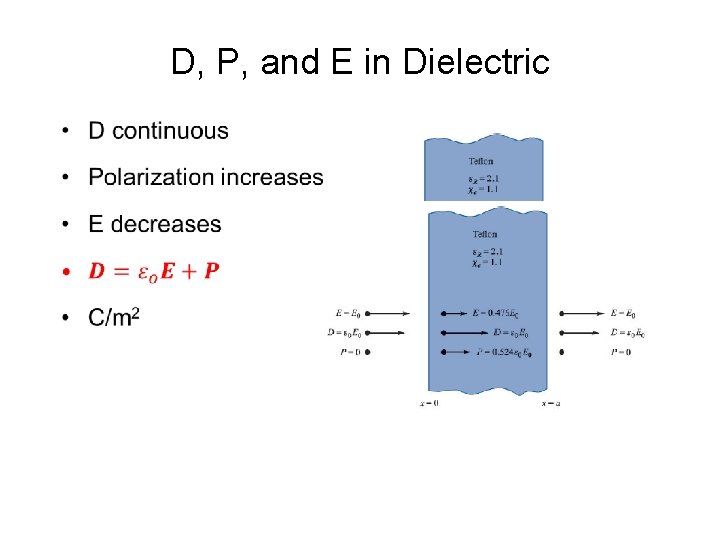
D, P, and E in Dielectric •

Charge Densities Taking the previous results and using the divergence theorem, we find the point form expressions: Bound Charge: Total Charge: Free Charge:

Electric Susceptibility and the Dielectric Constant A stronger electric field results in a larger polarization in the medium. In a linear medium, the relation between P and E is linear, and is given by: where e is the electric susceptibility of the medium. We may now write: where the dielectric constant, or relative permittivity is defined as: Leading to the overall permittivity of the medium: where

Isotropic vs. Anisotropic Media In an isotropic medium, the dielectric constant is invariant with direction of the applied electric field. This is not the case in an anisotropic medium (usually a crystal) in which the dielectric constant will vary as the electric field is rotated in certain directions. In this case, the electric flux density vector components must be evaluated separately through the dielectric tensor. The relation can be expressed in the form:

Permittivity of Materials • Typical permittivity for various solids and liquids. – – – Teflon – 2 Plastics - 3 -6 Ceramics 8 -10 Titanates>100 Acetone 2 1 Water 78 • Actual dielectric “constant” varies with: – Temperature – Direction – Field Strength – Frequency – Real & Imaginary components

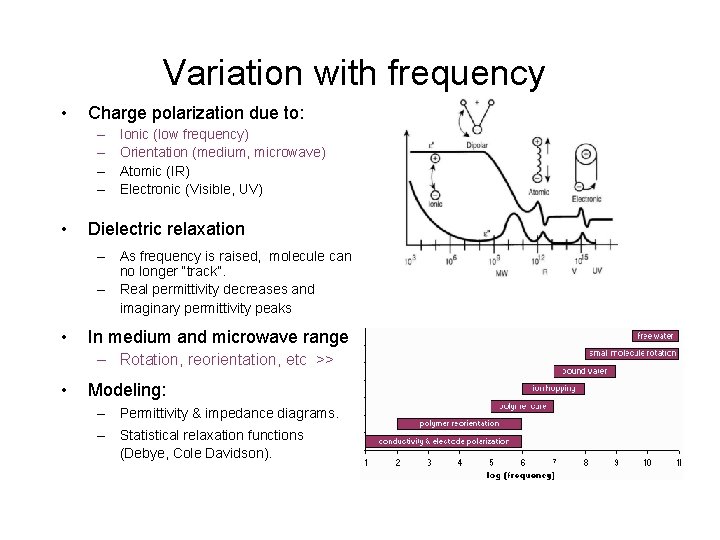
Variation with frequency • Charge polarization due to: – – • Ionic (low frequency) Orientation (medium, microwave) Atomic (IR) Electronic (Visible, UV) Dielectric relaxation – As frequency is raised, molecule can no longer “track”. – Real permittivity decreases and imaginary permittivity peaks • In medium and microwave range – Rotation, reorientation, etc >> • Modeling: – Permittivity & impedance diagrams. – Statistical relaxation functions (Debye, Cole Davidson).

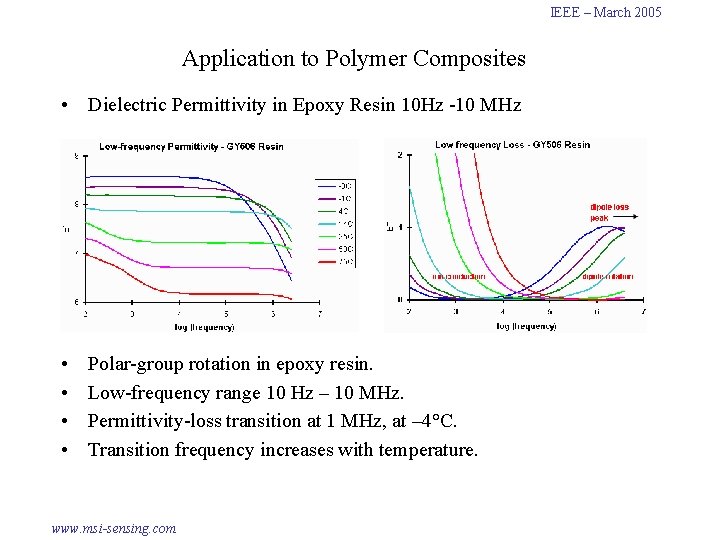
IEEE – March 2005 Application to Polymer Composites • Dielectric Permittivity in Epoxy Resin 10 Hz -10 MHz • • Polar-group rotation in epoxy resin. Low-frequency range 10 Hz – 10 MHz. Permittivity-loss transition at 1 MHz, at – 4°C. Transition frequency increases with temperature. www. msi-sensing. com

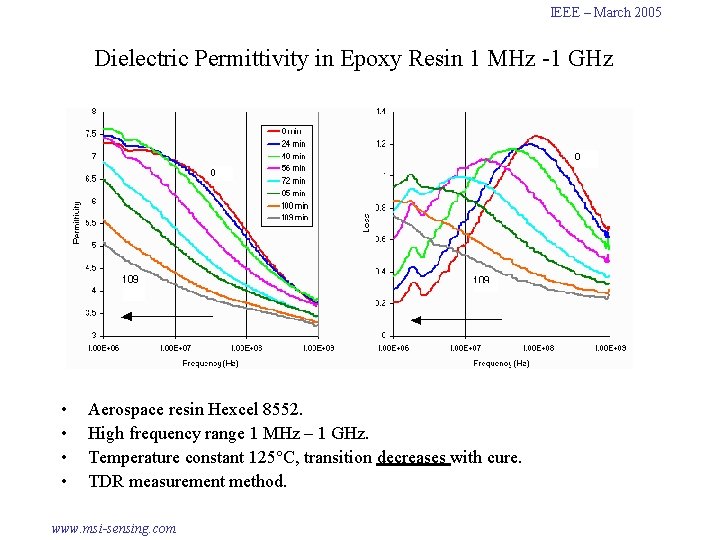
IEEE – March 2005 Dielectric Permittivity in Epoxy Resin 1 MHz -1 GHz • • Aerospace resin Hexcel 8552. High frequency range 1 MHz – 1 GHz. Temperature constant 125°C, transition decreases with cure. TDR measurement method. www. msi-sensing. com

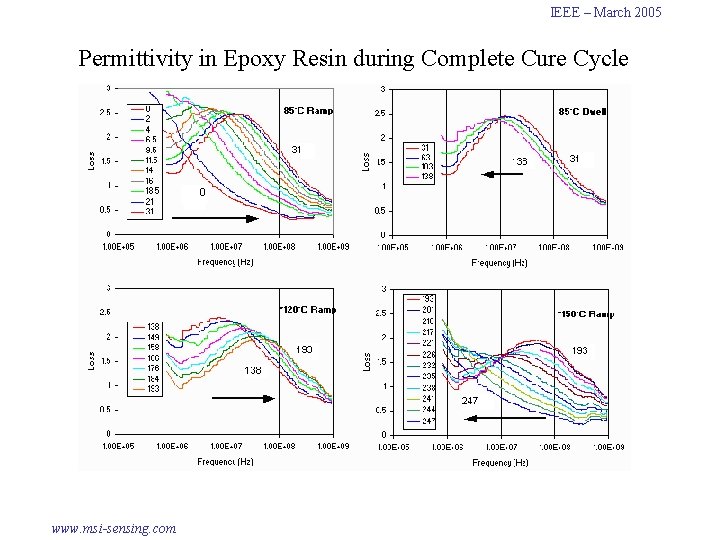
IEEE – March 2005 Permittivity in Epoxy Resin during Complete Cure Cycle www. msi-sensing. com

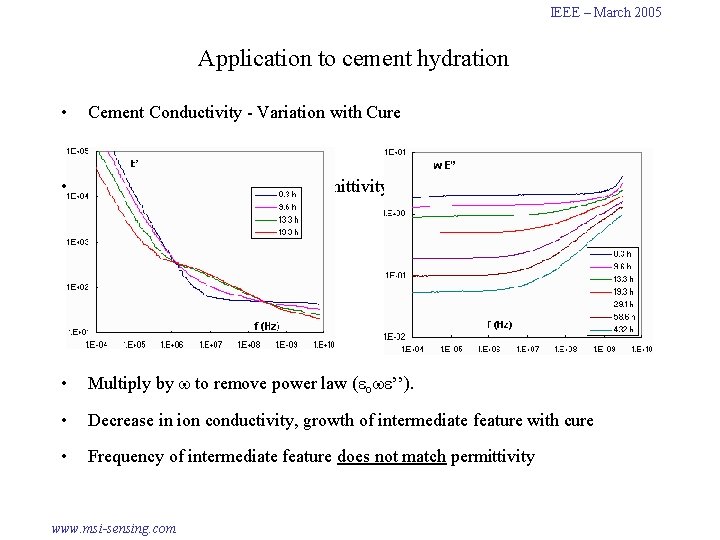
IEEE – March 2005 Application to cement hydration • Cement Conductivity - Variation with Cure • Imaginary counterpart of real permittivity ( ’’). • Multiply by to remove power law ( o ’’). • Decrease in ion conductivity, growth of intermediate feature with cure • Frequency of intermediate feature does not match permittivity www. msi-sensing. com

IEEE – March 2005 Cement Cure -Dielectric Relaxation Model Requirements: • • Provide free-relaxation, two intermediate-frequency relaxations Provide conductivity and electrode polarization Debye for free & medium. Cole-Davidson for low. (literature, biosystems) Combined 9 variables fit over entire range, real & imaginary, 2 -stage fit, f = 8. 2 ps www. msi-sensing. com

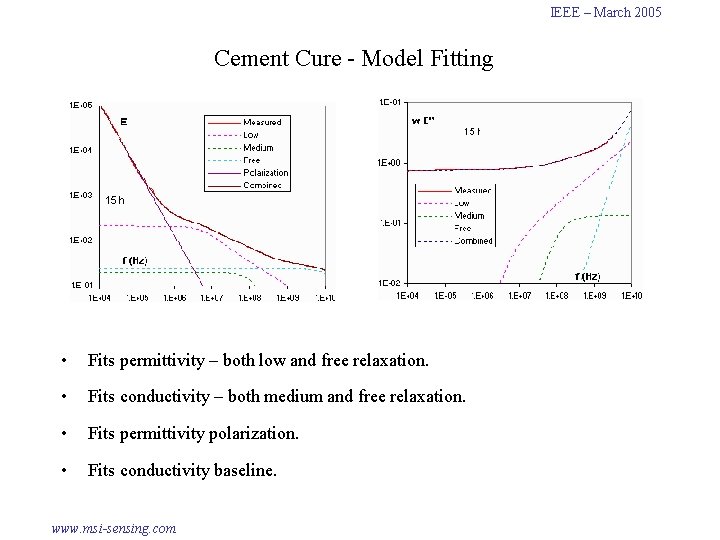
IEEE – March 2005 Cement Cure - Model Fitting • Fits permittivity – both low and free relaxation. • Fits conductivity – both medium and free relaxation. • Fits permittivity polarization. • Fits conductivity baseline. www. msi-sensing. com

IEEE – March 2005 Other applications • Other Applications – – – – Bio Liquid Crystal Composite polymers Titanates Wireless characterization MRI dyes Ground water monitoring Oil Drilling fluid characterization (GPR)

Boundary Condition for Tangential Electric Field E Since E is conservative, we setup line integral straddling both dielectrics: Left and right sides cancel, so Leading to Continuity for tangential E And Discontinuity for tangential D E same, D higher in high permittivity material

Boundary Condition for Normal Displacement D Apply Gauss’ Law to the cylindrical volume straddling both dielectrics n s Flux enters and exits only through top and bottom surfaces, zero on sides Leading to Continuity for normal D (for ρS = 0) And Discontinuity for normal E D same. E lower in high permittivity material

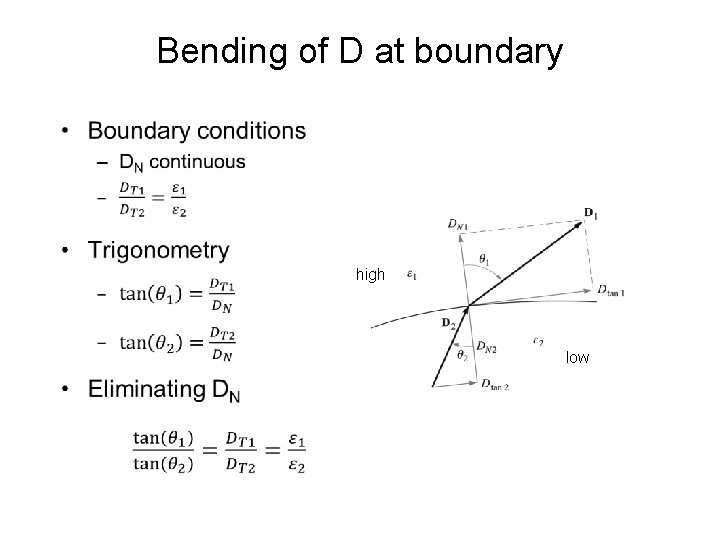
Bending of D at boundary • high low

Example •

Example (continued) • Polarization up, E field down, D maintains continuity

Example

Quiz 2 – Problem 4. 21