CONDITIONAL STATEMENTS Section 2 1 Geometry Pre AP

CONDITIONAL STATEMENTS Section 2– 1 Geometry Pre. AP, Revised © 2013 viet. dang@humble. k 12. tx. us 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 1

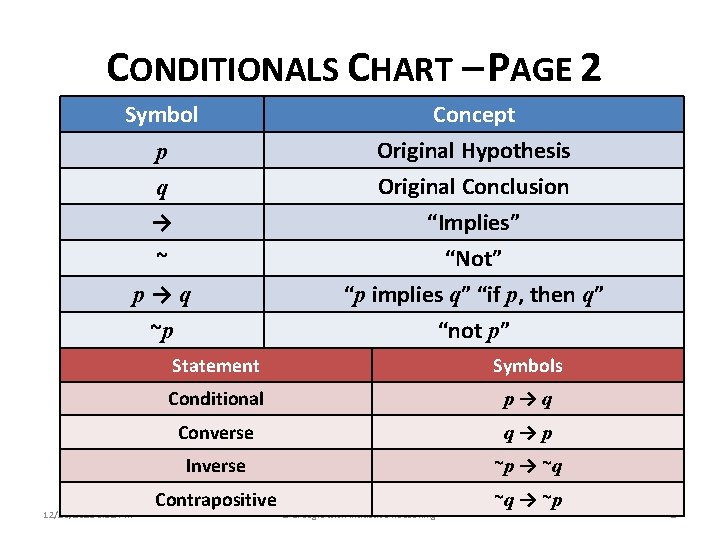
CONDITIONALS CHART – PAGE 2 Symbol p q → ~ p→q ~p 12/28/2021 8: 32 PM Concept Original Hypothesis Original Conclusion “Implies” “Not” “p implies q” “if p, then q” “not p” Statement Symbols Conditional p→q Converse q→p Inverse ~p → ~q Contrapositive 2 -1: Logic with Inductive Reasoning ~q → ~p 2

CONDITIONALS – PAGE 3 A. If p, then q B. Notation: p → q (if p then q) C. HYPOTHESIS – all words after “If” and before comma D. CONCLUSION – all words after “Then” 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 3

EXAMPLE 1 In this statement, “If a polygon is a hexagon, then it has exactly six sides” state the hypothesis and conclusion Subject Predicate A polygon is a hexagon is a polygon with six sides. If it is a hexagon, then it is a polygon with six sides. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 4

EXAMPLE 2 In this statement, “a number is a rational number if it is an integer. ” State the hypothesis and conclusion. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 5

EXAMPLE 3 Rewrite this conditional statement in if-then form, “All 90° angles are right angles. ” 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 6

YOUR TURN Write an example of a conditional statement (if then) about a topic in geometry. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 7

TRUTH VALUES – PAGE 5 A. B. C. D. E. F. G. H. I. J. Determining whether a statement is TRUE or FALSE. True: To prove that the conclusion is true every time the hypothesis is satisfied. False: To prove if it is false, one has to find an example in which the conclusion is not true when the hypothesis is satisfied. A conditional is FALSE ONLY when hypothesis is true and conclusion is false. To show false you need a COUNTEREXAMPLE. Counterexample – example that proves a statement is false. Related conditional statements that have the same TRUTH VALUE are logically equivalent. Create a table (can all be T or all F) Conditional and Contrapositive always the same Converse and Inverse always the same 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 8

EXAMPLE 4 In this statement, “If this month is August, then next month is September” state whether the conditional statement is true. If it is false, provide a counterexample. When the hypothesis is true, the conclusion is also true because September follows August. So the conditional is true. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 9

EXAMPLE 5 In this statement, “If n 2 = 144, then n = 12” state whether the conditional statement is true. If it is false, provide a counterexample. When the hypothesis is true, the conclusion is also false because if n = – 12, n 2 also equals 144. So the conditional is false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 10

YOUR TURN In this statement, “If it is February, then there are only 28 days in the month” state whether the conditional statement is true. If it is false, provide a counterexample. When the hypothesis is true, the conclusion is also false because if February can have 29 days in a leap year. So the conditional is false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 11

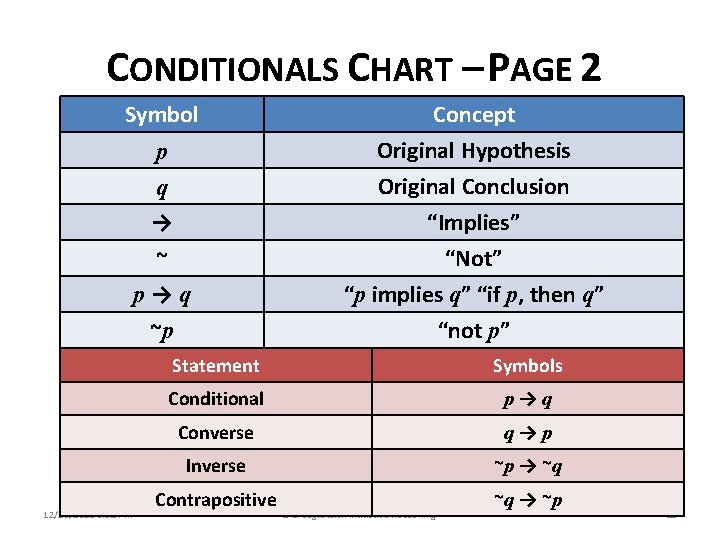
CONDITIONALS CHART – PAGE 2 Symbol p q → ~ p→q ~p 12/28/2021 8: 32 PM Concept Original Hypothesis Original Conclusion “Implies” “Not” “p implies q” “if p, then q” “not p” Statement Symbols Conditional p→q Converse q→p Inverse ~p → ~q Contrapositive 2 -1: Logic with Inductive Reasoning ~q → ~p 12

CONDITIONALS – PAGE 3 A. If p, then q B. Notation: p → q (if p then q) C. HYPOTHESIS – all words after “If” and before comma D. CONCLUSION – all words after “Then” 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 13

EXAMPLE 6 In this statement, “If a polygon is a hexagon, then it has exactly six sides” state the hypothesis and conclusion Subject Predicate A polygon is a hexagon is a polygon with six sides. If it is a hexagon, then it is a polygon with six sides. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 14

EXAMPLE 7 In this statement, “a number is a rational number if it is an integer. ” State the hypothesis and conclusion. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 15

EXAMPLE 8 Rewrite this conditional statement in if-then form, “All 90° angles are right angles. ” 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 16

YOUR TURN Write an example of a conditional statement (if then) about a topic in geometry. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 17

CONVERSE, INVERSE, AND CONTRAPOSITIVE – PAGE 4 A. Converse 1. The CONVERSE is formed by REVERSING the hypotheses and conclusion. 2. Notation: q → p (if q then p) B. Inverse 1. The INVERSE is formed by NEGATING the hypotheses and conclusion. 2. Notation: ~p → ~q (if not p then not q) C. Contrapositive 1. The CONTRAPOSITIVE is formed by REVERSING and NEGATING the hypotheses and conclusion. 2. Notation: ~q → ~p (if not q then not p) 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 18

EXAMPLE 9 In this statement, “If a polygon is a hexagon, then it has six sides” state the converse and determine whether it is true of false. If it is a hexagon, then it is a polygon with six sides. If a polygon has exactly six sides, then it is a hexagon. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 19

EXAMPLE 10 In this statement, “All squares are rectangles” state the converse and determine whether it is true or false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 20

YOUR TURN In this statement, “If an animal is an adult insect, then it has six legs” state the converse and determine whether it is true or false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 21

EXAMPLE 11 In this statement, “If a polygon is a hexagon, then it has six sides” state the inverse and determine whether it is true of false. If it is a hexagon, then it is a polygon with six sides. If the polygon is NOT a hexagon, then it is NOT a polygon with six sides. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 22

EXAMPLE 12 In this statement, “If a number is even then it is divisible by two” state the converse and determine whether it is true or false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 23

YOUR TURN In this statement, “If an animal is an adult insect, then it has six legs” state the inverse and determine whether it is true or false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 24

EXAMPLE 13 In this statement, “If a polygon is a hexagon, then it has six sides” state the contrapositive and determine whether it is true of false. If it is a hexagon, then it is a polygon with six sides. If a polygon does NOT have exactly six sides, then it is NOT a hexagon. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 25

EXAMPLE 14 In this statement, “If you are a guitar player, then you are a musician, ” state the contrapositive and determine whether it is true or false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 26

YOUR TURN In this statement, “If m A = 99°, then A is obtuse” state the contrapositive and determine whether it is true or false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 27

EXAMPLE 15 Fill out these statements below and identify whether it is true or false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 28

YOUR TURN In this statement, “If I measure two angles which are acute, then they are congruent” state whether the conditional statement is true. If it is false, provide a counterexample. You can have acute angles with measures of 80° and 30°. In this case, the hypothesis is true, but the conclusion is false. 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 29

ASSIGNMENT Page 77 8, 10 -13 all, 16, 20 -23, 25, 28, 31, 37, 38 12/28/2021 8: 32 PM 2 -1: Logic with Inductive Reasoning 30