Conditional Statements M 260 2 2 Deductive Reasoning







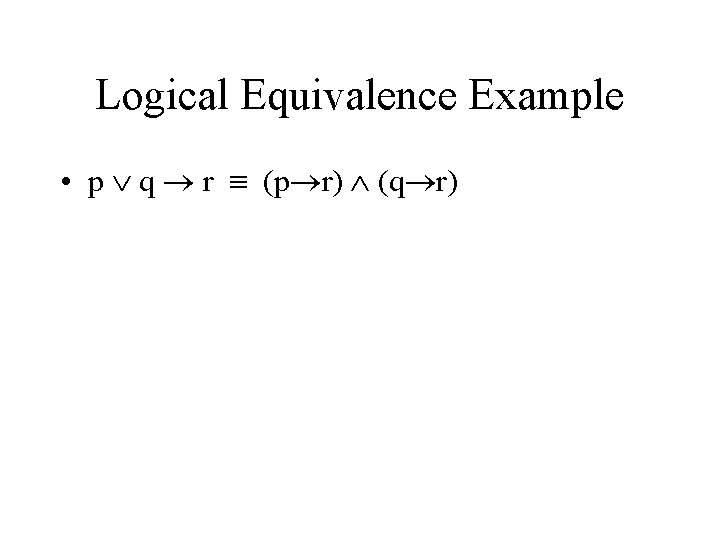

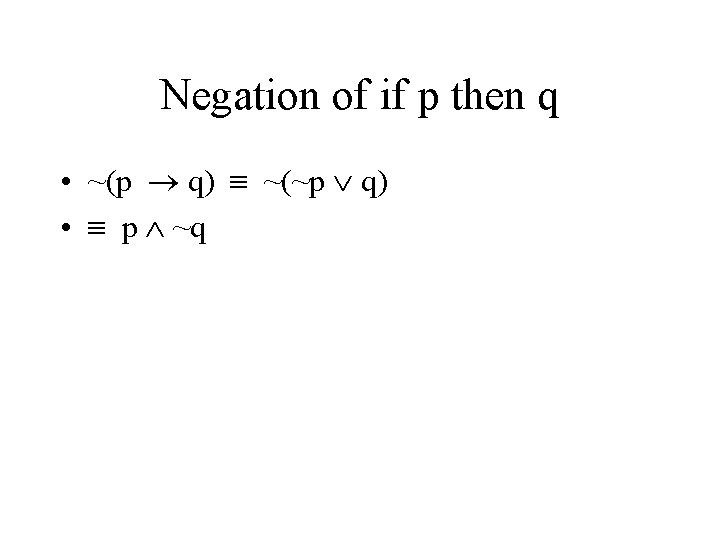



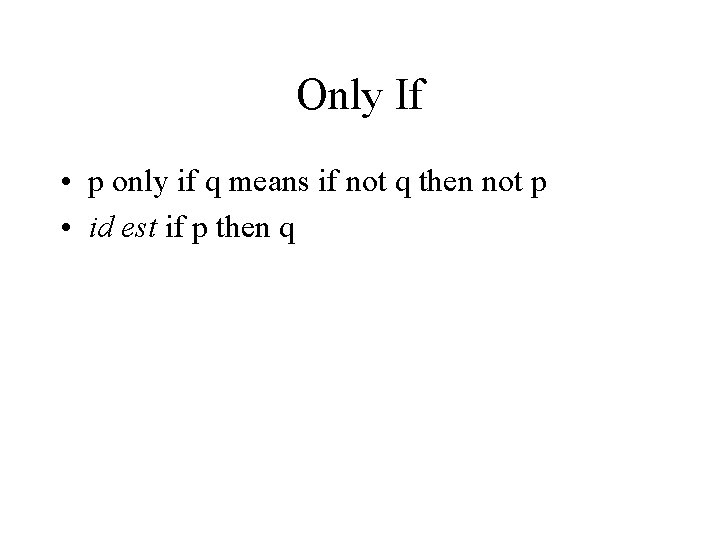


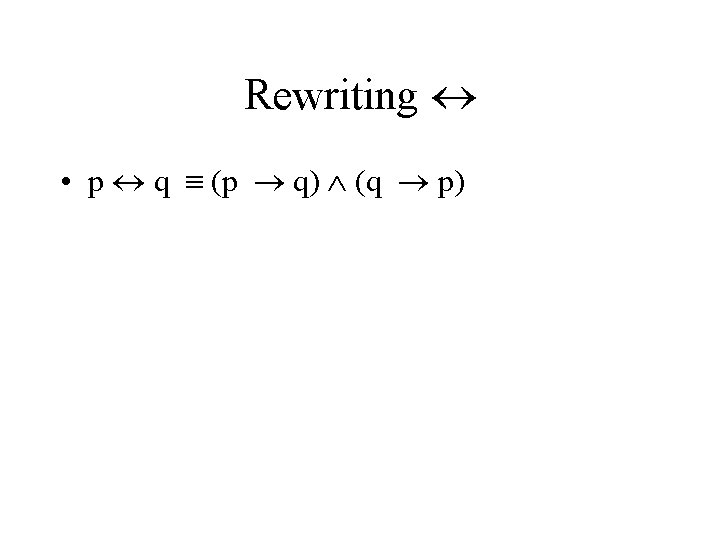





- Slides: 28

Conditional Statements M 260 2. 2

Deductive Reasoning • • Proceeds from a hypothesis to a conclusion. If p then q. p q hypothesis conclusion

Conditional Example • If you show up for work on Monday morning, then you will get the job. • When is the statement false? • Answer--Only when the hypothesis is true and the conclusion is false.

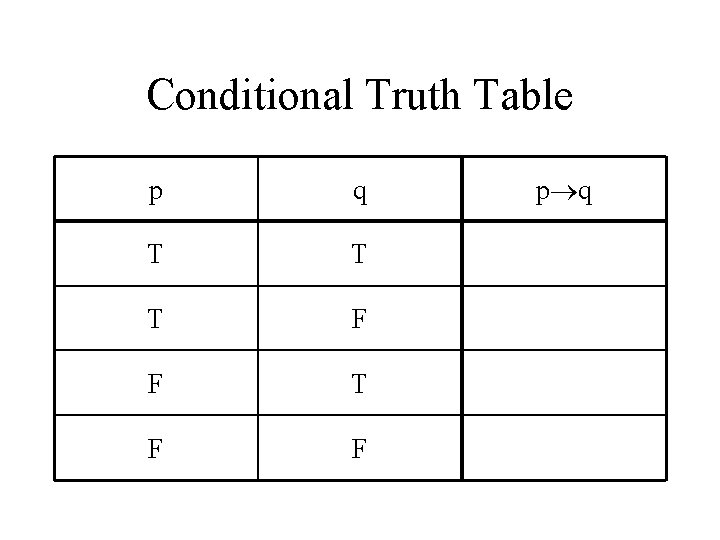
Conditional Truth Table p q T T T F F p q

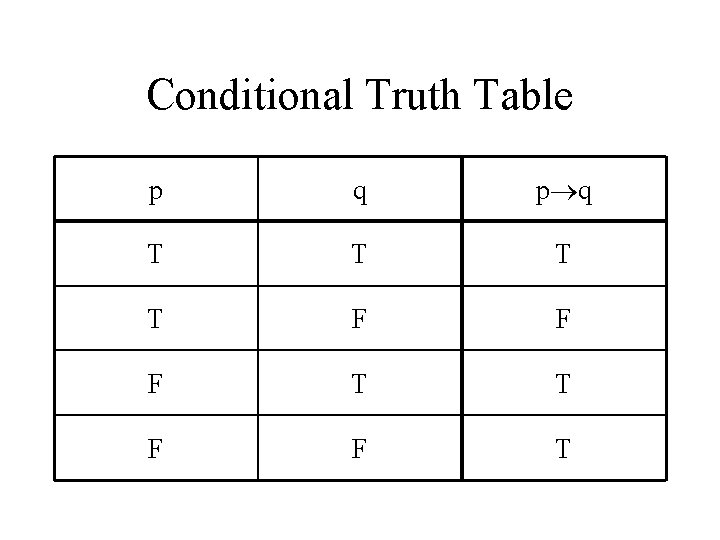
Conditional Truth Table p q T T F F F T T F F T

Conditional is vacuously true when hypothesis is false.

Precedence of Logical Operators • • ~ and

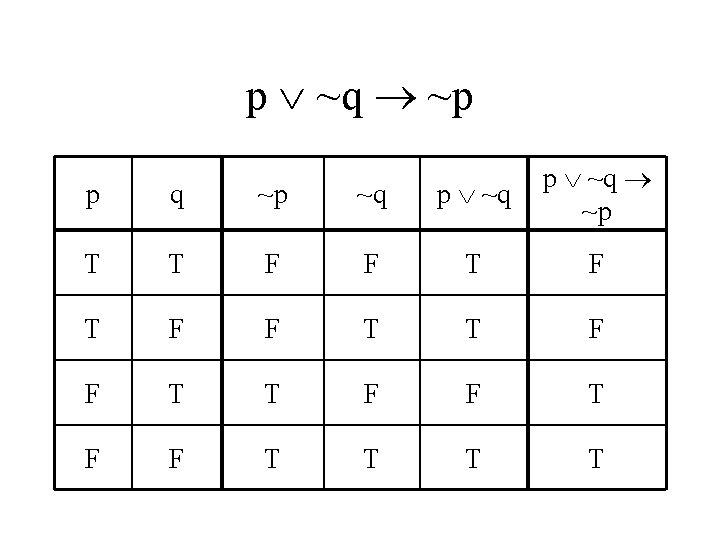
Precedence Examples • p ~q ~p • Order is ~, , • (p (~q)) (~p)

p ~q ~p

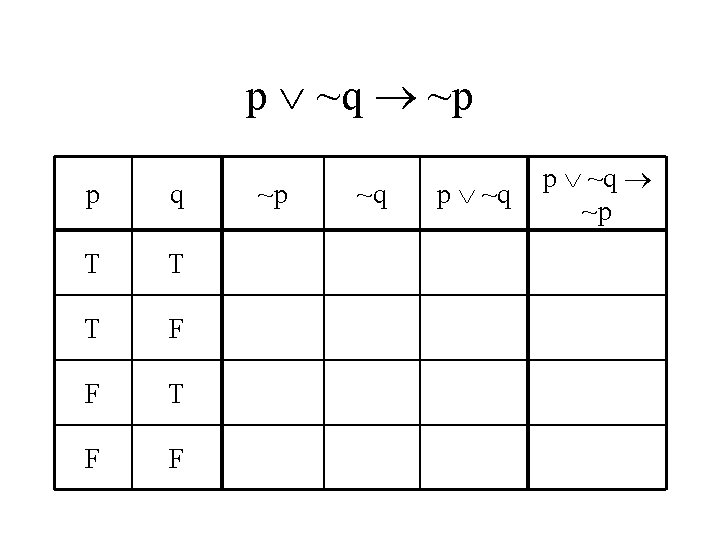
p ~q ~p p q T T T F F ~p ~q p ~q ~p

p ~q ~p p q ~p ~q p ~q ~p T T F F T T F F T T T T

Logical Equivalence • Statement Forms are logically equivalent if, and only if, they have the same truth tables. • P Q
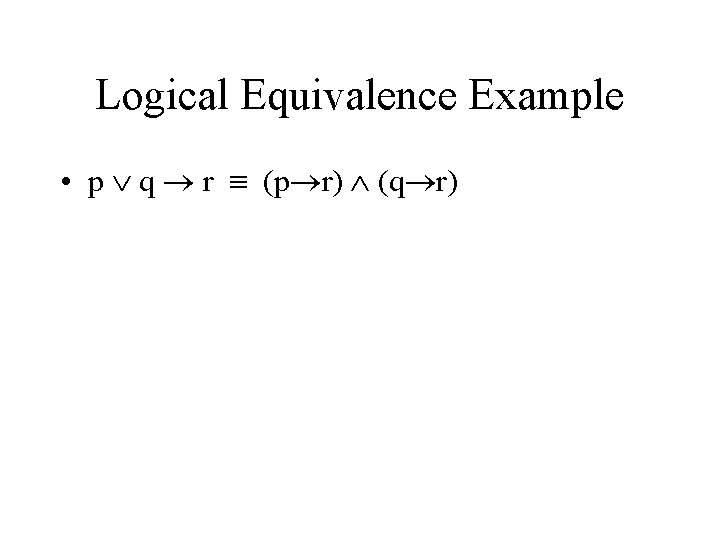
Logical Equivalence Example • p q r (p r) (q r)

Rewriting • p q ~p q • Either you get to work on time or you are fired • If you do not get to work on time, then you are fired.
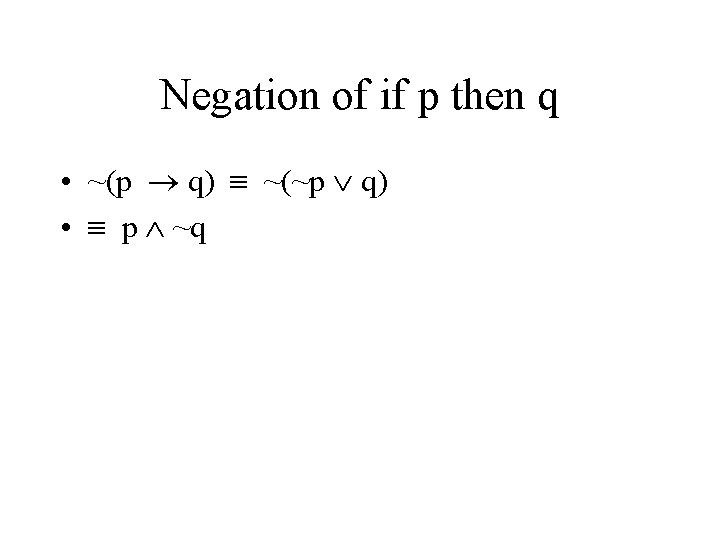
Negation of if p then q • ~(p q) ~(~p q) • p ~q

Contrapositive • Contrapositive of if p then q is if ~q then ~p • p q ~p • Conditional and contrapositive are logically equivalent.

Converse • Converse of if p then q is if q then p • Converse (p q) is (q p) • Conditional and converse are NOT logically equivalent.

Inverse • Inverse of if p then q is if ~p then ~q • Inverse (p q) is (~p ~q) • Conditional and inverse are NOT logically equivalent. • Converse and inverse are logically equivalent.
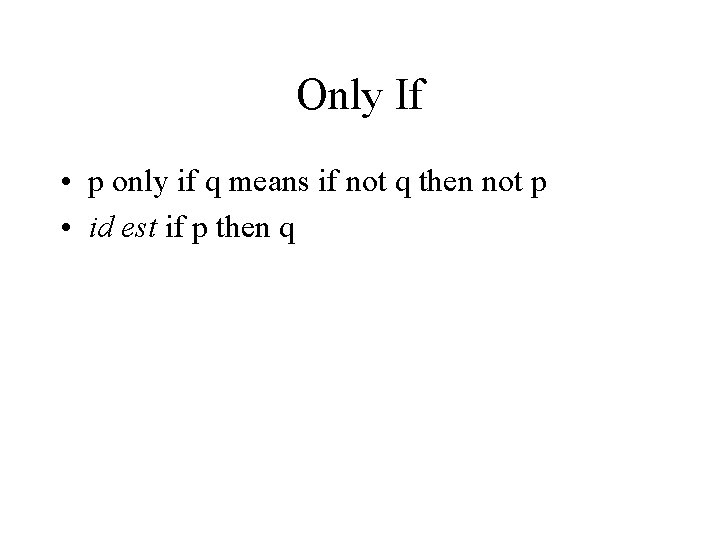
Only If • p only if q means if not q then not p • id est if p then q

Only If Example • John will break the world’s record for the mile only if • he runs the mile in under four minutes.

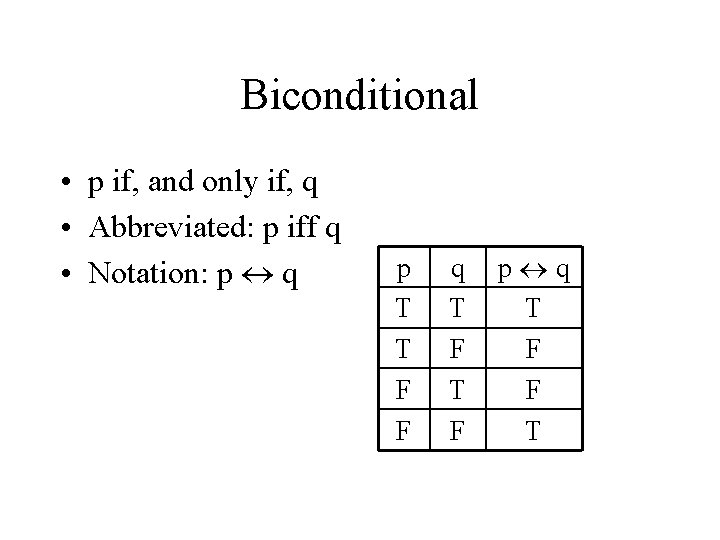
Biconditional • p if, and only if, q • Abbreviated: p iff q • Notation: p q p T T F F q T F p q T F F T

Precedence of Logical Operators • • ~ and
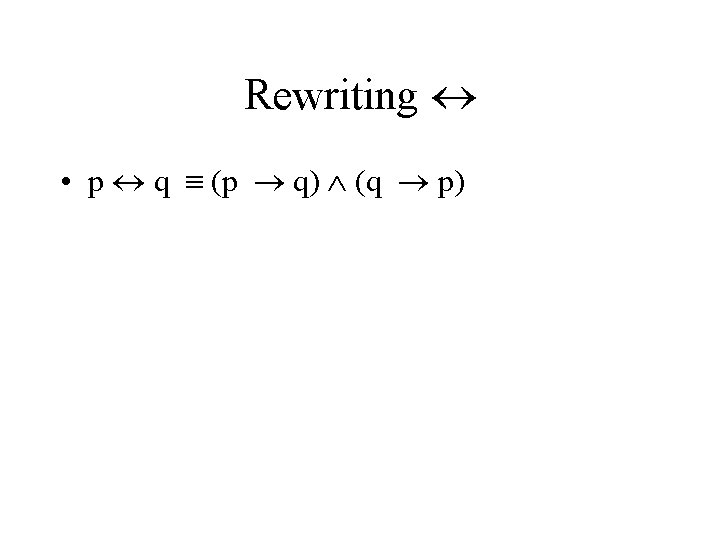
Rewriting • p q (p q) (q p)

Sufficient Condition • r is a sufficient condition for s • If r then s • r s

Necessary Condition • • • r is a necessary condition for s If not r then not s ~r ~s s only if r If s then r

Necessary and Sufficient • r is a necessary and sufficient condition for s • r if, and only if, s • r s

Practice Necessary/Sufficient • Use “John is eligible to vote” and “John is at least 18 years old” to make • A conditional statement: • A necessary statement: • A sufficient statement:

Formal vs. Conversational Logic • Unrelated conclusions • Understood biconditionals