Conditional Statements Lecture 2 Section 1 2 Thu

The Conditional A conditional statement is a statement of the form p q ¢

Truth Table for the Conditional p q is true if p is false or

Example: Conditional Statements “If it is raining, then I am carrying an umbrella. ”

The Contrapositive The contrapositive of p q is q p. ¢ The statements p

The Converse and the Inverse The converse of p q is q p. ¢

The Biconditional ¢ ¢ The statement p q is the biconditional of p and

Exclusive-Or ¢ ¢ The statement p q is the exclusive-or of p and q.

Exclusive-Or p q means “one or the other, but not both. ” ¢ p

The NAND Operator The statement p | q means not both p and q.

The NAND Operator ¢ p | q is defined by p q p|q T

The NAND Operator ¢ The three basic operators may be defined in terms of

The NOR Operator The statement p q means neither p nor q. ¢ The

The NOR Operator ¢ p q is defined by p q T T F

The NOR Operator ¢ The three basic operators may be defined in terms of

Slides: 16

Download presentation

Conditional Statements Lecture 2 Section 1. 2 Thu, Jan 13, 2005

The Conditional A conditional statement is a statement of the form p q ¢ p is the hypothesis. ¢ q is the conclusion. ¢ Read p q as “p implies q. ” ¢

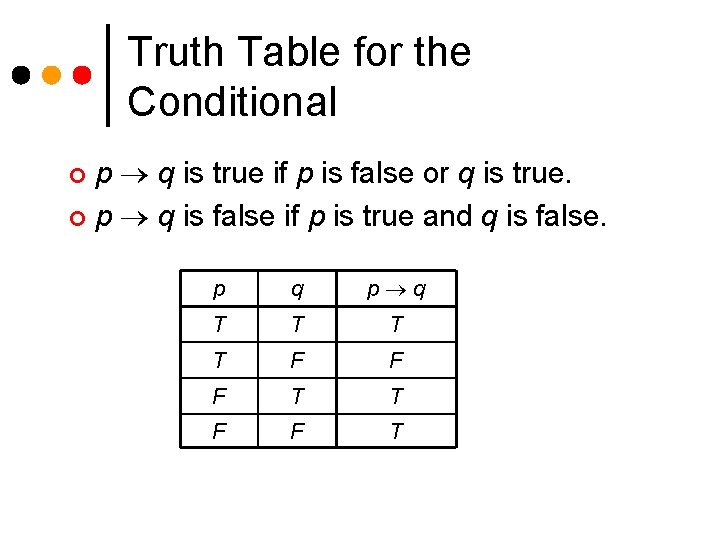
Truth Table for the Conditional p q is true if p is false or q is true. ¢ p q is false if p is true and q is false. ¢ p q T T F F F T T F F T

Example: Conditional Statements “If it is raining, then I am carrying an umbrella. ” ¢ This statement is true ¢ when I am carrying an umbrella (whether or not it is raining), and l when it is not raining (whether or not I am carrying an umbrella). l

The Contrapositive The contrapositive of p q is q p. ¢ The statements p q and q p are logically equivalent. ¢

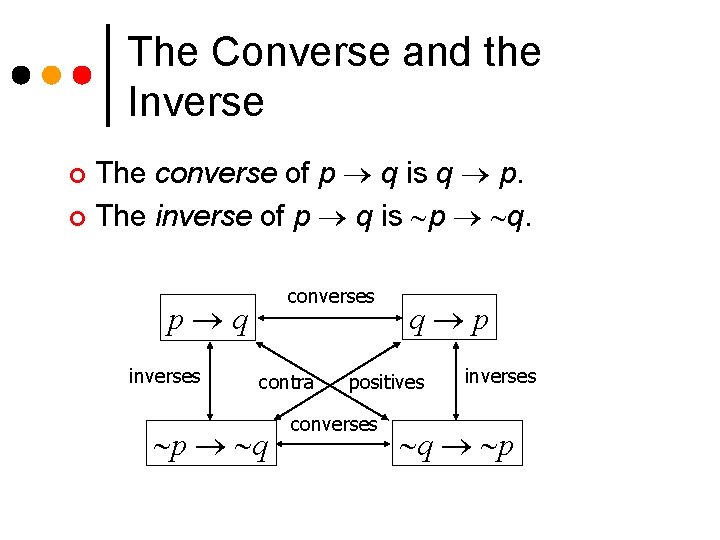
The Converse and the Inverse The converse of p q is q p. ¢ The inverse of p q is p q. ¢ converses p q inverses contra p q q p positives converses inverses q p

Is this logical?

The Biconditional ¢ ¢ The statement p q is the biconditional of p and q. p q is logically equivalent to (p q) (q p). p q T T F F F T

Exclusive-Or ¢ ¢ The statement p q is the exclusive-or of p and q. p q is defined by p q T T F T F T T F F F

Exclusive-Or p q means “one or the other, but not both. ” ¢ p q is logically equivalent to (p q) (q p) ¢ p q is also logically equivalent to (p q) (q p) ¢

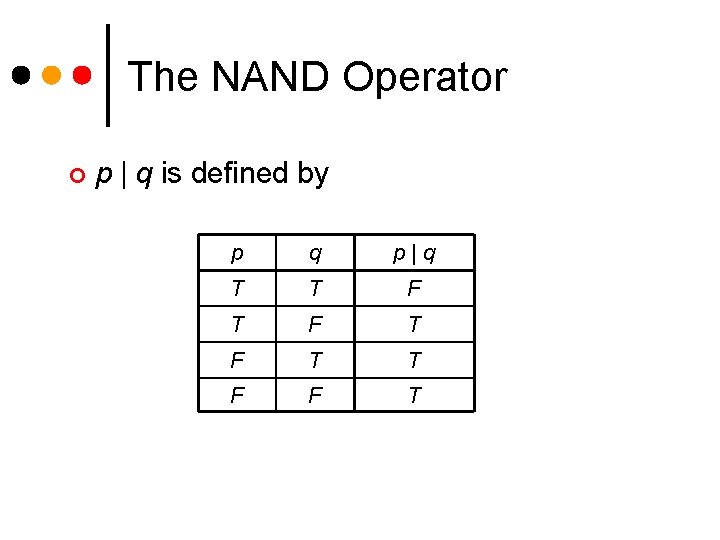
The NAND Operator The statement p | q means not both p and q. ¢ The operator | is also called the Scheffer stroke or NAND. ¢ NAND stands for “Not AND. ” ¢ p | q is logically equivalent to (p q). ¢

The NAND Operator ¢ p | q is defined by p q p|q T T F T F T T F F T

The NAND Operator ¢ The three basic operators may be defined in terms of NAND. p p | p. l p q (p | q) | (p | q). l p q (p | p) | (q | q). l

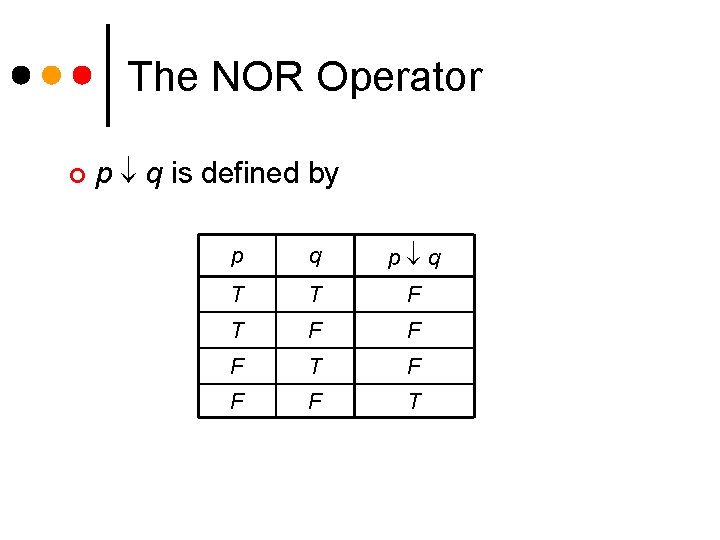
The NOR Operator The statement p q means neither p nor q. ¢ The operator is also called the Pierce arrow or NOR. ¢ NOR stands for “Not OR. ” ¢ p q is logically equivalent to (p q). ¢

The NOR Operator ¢ p q is defined by p q T T F F F T

The NOR Operator ¢ The three basic operators may be defined in terms of NOR. p p p. l p q (p q). l p q (p p) (q q). l