Conditional Random Fields Mark Stamp CRF 1 Intro

Conditional Random Fields Mark Stamp CRF 1

Intro q Hidden o o Markov Model (HMM) used in Bioinformatics Natural language processing Speech recognition Malware detection/analysis q And many, many other applications q Bottom line: HMMs are very useful o Everybody knows that! CRF 2

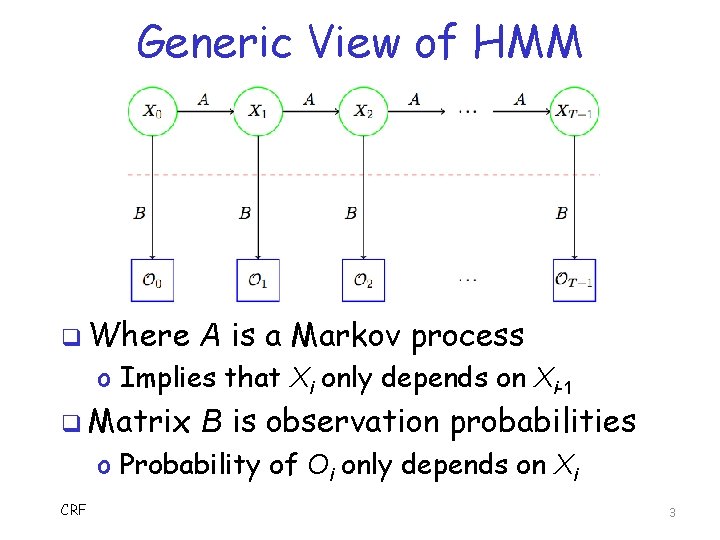
Generic View of HMM q Where A is a Markov process o Implies that Xi only depends on Xi-1 q Matrix B is observation probabilities o Probability of Oi only depends on Xi CRF 3

HMM Limitations q Assumptions o Observation depends on current state o Current state depends on previous state o Strong independence assumption q Often independence is not realistic o Observation can depend on several states o And/or current state might depend on several previous states CRF 4

HMMs q Within HMM framework, we can… q Increase N, number of hidden states q And/or higher order Markov process o “Order 2” means hidden state depends on 2 immediately previous hidden states o Order > 1 relaxes independence constraint q More hidden states, more “breadth” q Higher order, increased “depth” CRF 5

Beyond HMMs q HMMs do not fit some situations o For example, arbitrary dependencies on state transitions and/or observations q Here, focus on generalization of HMM o Conditional Random Fields (CRF) q There are other generalizations o We mention a few q Mostly CRF focused on the “big picture” 6

HMM Revisited q Illustrates graph structure of HMM o That is, HMM is a directed line graph q Can other types of graphs work? q Would they make sense? CRF 7

MEMM q In HMM, observation sequence O is related to states X via B matrix o And O affects X in training, not scoring o Might want X to depend on O in scoring q Maximum Entropy Markov Model o State Xi is function of Xi-1 and Oi q MEMM focused on “problem 2” o That is, determine (hidden) states CRF 8

Generic MEMM q How does this differ from HMM? o State Xi is function of Xi-1 and Oi o Cannot generate Oi using the MEMM, while we can do so using HMM CRF 9

MEMM vs HMM q HMM Find “best” state sequence X o That is, solve HMM Problem 2 o Solution is X that maximizes P(X|O) = Π P(Oi|Xi) Π P(Xi|Xi-1) q MEMM Find “best” state sequence X o Solution is X that maximizes P(X|O) = Π P(Xi|Xi-1, Oi) where P(x|y, o) = 1/Z(o, y) exp(Σwjfj(o, x)) CRF 10

MEMM vs HMM q Note Σwj fj(o, x) in MEMM probability o This sum is over entire sequence o Any useful feature of input observation can affect probability q MEMM more “general” in this sense o As compared to HMM, that is q But MEMM creates a new problem o A problem that does not occur in HMM CRF 11

Label Bias Problem q MEMM uses dynamic programming (DP) o Also known as the Viterbi algorithm q HMM (problem 2) does not use DP o HMM α-pass uses sum, DP uses max q In MEMM probability is “conserved” o Probability must be split between successor states (not so in HMM) o Is this good or bad? CRF 12

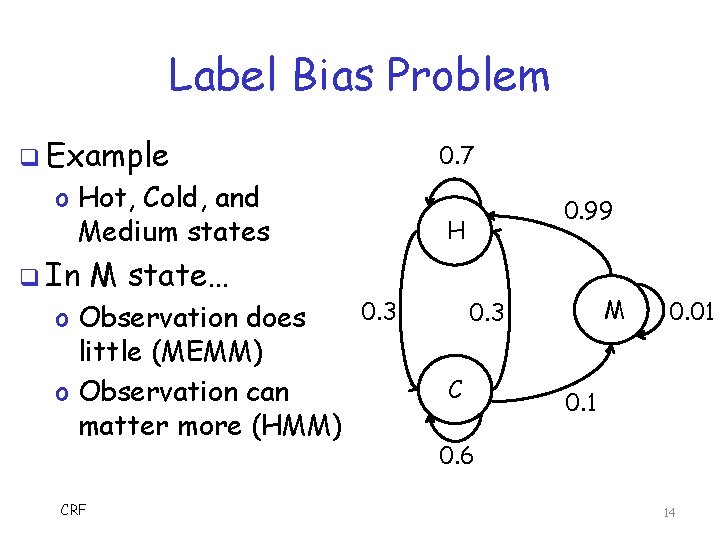
Label Bias Problem q Only one possible successor in MEMM? o All probability passed along to that state o In effect, observation is ignored o More generally, if one dominant successor, observation doesn’t matters much q CRF solves label bias problem of MEMM o So, observation matters q We CRF won’t go into details here… 13

Label Bias Problem q Example o Hot, Cold, and Medium states q In 0. 99 H M state… 0. 3 o Observation does little (MEMM) o Observation can matter more (HMM) CRF 0. 7 M 0. 3 C 0. 01 0. 6 14

Conditional Random Fields q CRFs a generalization of HMMs q Generalization to other graphs o Undirected graphs q Linear Chain CRF is simplest case q But also generalizes to arbitrary (undirected) graphs o That is, can have arbitrary dependencies between states and observations CRF 15

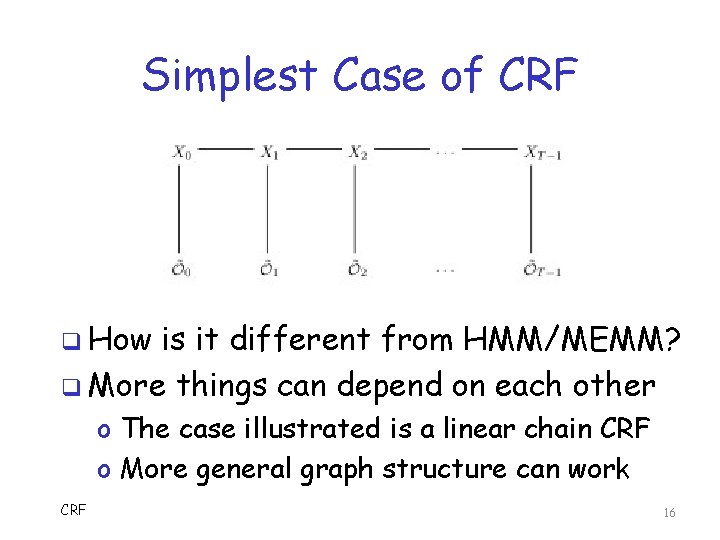
Simplest Case of CRF q How is it different from HMM/MEMM? q More things can depend on each other o The case illustrated is a linear chain CRF o More general graph structure can work CRF 16

Another View q Next, consider deeper connection between HMM and CRF q But first, we need some background o Naïve Bayes o Logistic regression q These topics are very useful in their own right… o …so wake up and pay attention! CRF 17

What Are We Doing Here? q Recall, O observation, X is state q Ideally, want to model P(X, O) o All possible interactions of Xs and Os q But P(X, O) involves lots of parameters o Like the complete covariance matrix o Lots of data needed for “training” o And too much work to train q Generally, CRF this problem is intractable 18

What to Do? q Simplify, simplify, simplify… o Need to make problem tractable o And then hope we get decent results q In Naïve Bayes, assume independence q In regression analysis, try to fit specific function to data q Eventually, we’ll see this is relevant o Wrt HMMs and CRFs, that is CRF 19

Naïve Bayes q Why is it “naïve”? q Assume features in X are independent o Probably not true, but simplifies things o And often works well in practice q Why does independence simplify? o Recall covariance: For X = (x 1, …, xn) and Y = (y 1, …, yn), if means are 0, then Cov(X, Y) = (x 1 y 1 +…+ xnyn) / n CRF 20

Naïve Bayes q Independent implies covariance is 0 q If so, in covariance matrix only the diagonal elements are non-zero q Only need means and variances o Not the entire covariance matrix o Far fewer parameters to estimate o And a lot less data needed for training q Bottom CRF line: Practical solution 21

Naïve Bayes q Why is it “Bayes”? q Because it uses Bayes Theorem: o That is, o Or, o More generally, where Aj form partition CRF 22

Bayes Formula Example q Consider a test for an illegal drug o If you use drug, 98% positive (TPR = sensitivity) o If don’t use, 99% negative (TNR = specificity) o In overall population, 5/1000 use the drug q Let A = uses the drug, B = tests positive q Then =. 98 ×. 005 / (. 98 ×. 005 +. 01 ×. 995) = 0. 329966 = 33% CRF 23

Naïve Bayes q Why is this relevant? q Spse classify based on observation O o Compute P(X|O) = P(O|X) P(X) / P(O) o Where X is one possible class (state) o And P(O|X) is easy to compute q Repeat for all possible classes X o Biggest probability is most likely class X o Can ignore P(O) since it’s constant CRF 24

Regression Analysis q Generically, method for measuring relationship between 2 or more things o E. g. , house price vs size q First, we consider linear regression o Since it’s the simplest case q Then logistic regression o More complicated, but often more useful o Better for binary classifiers CRF 25

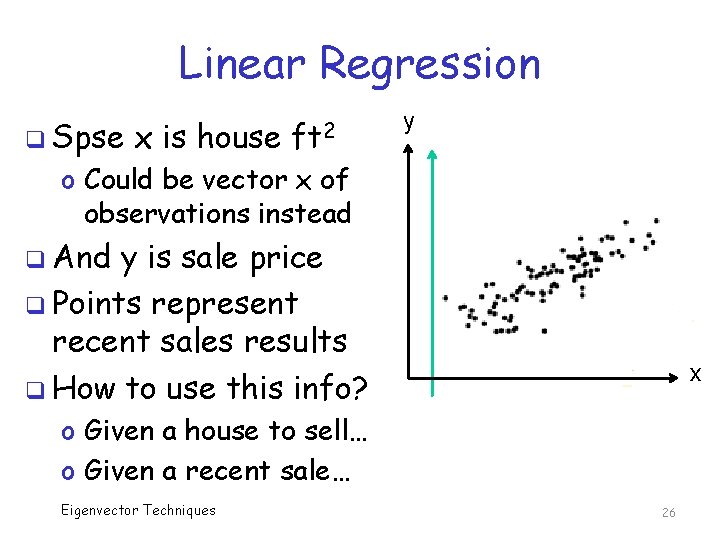
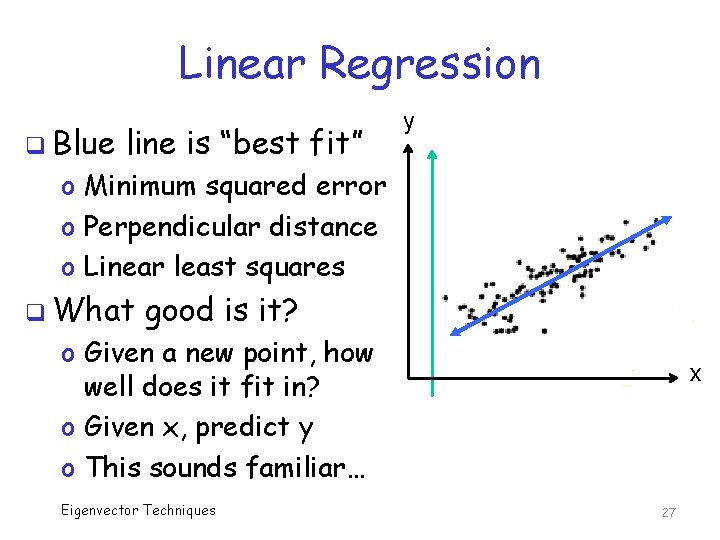
Linear Regression q Spse x is house ft 2 y o Could be vector x of observations instead q And y is sale price q Points represent recent sales results q How to use this info? x o Given a house to sell… o Given a recent sale… Eigenvector Techniques 26

Linear Regression q Blue line is “best fit” y o Minimum squared error o Perpendicular distance o Linear least squares q What good is it? o Given a new point, how well does it fit in? o Given x, predict y o This sounds familiar… Eigenvector Techniques x 27

Regression Analysis q In many problems, only 2 outcomes o Binary classifier, e. g. , malware vs benign o “Malware of specific type” vs “other” q Then x is an observation (vector) q But each y is either 0 or 1 o Linear regression not so good (Why? ) o A better idea logistic regression o Fit a logistic function instead of line CRF 28

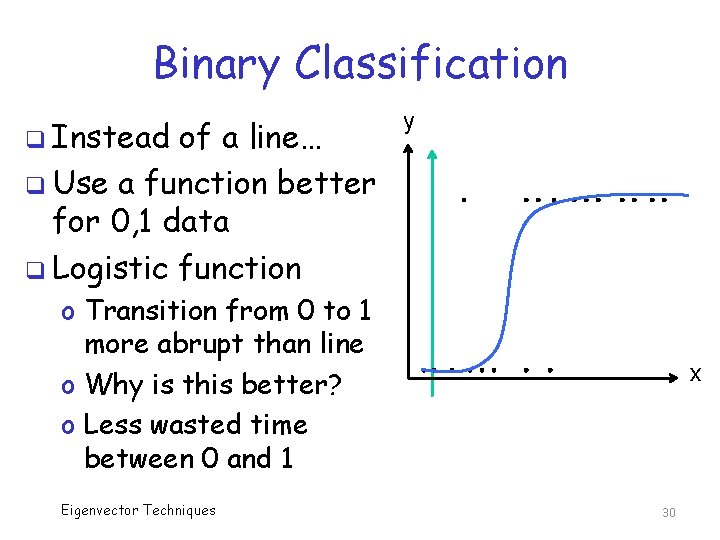
Binary Classification q Suppose we compute score for many files q Score is on x-axis q Output on y-axis y o 1 if file is malware o 0 if file is “other” x q Linear regression not very useful here Eigenvector Techniques 29

Binary Classification q Instead of a line… q Use a function better for 0, 1 data q Logistic function y o Transition from 0 to 1 more abrupt than line o Why is this better? o Less wasted time between 0 and 1 Eigenvector Techniques x 30

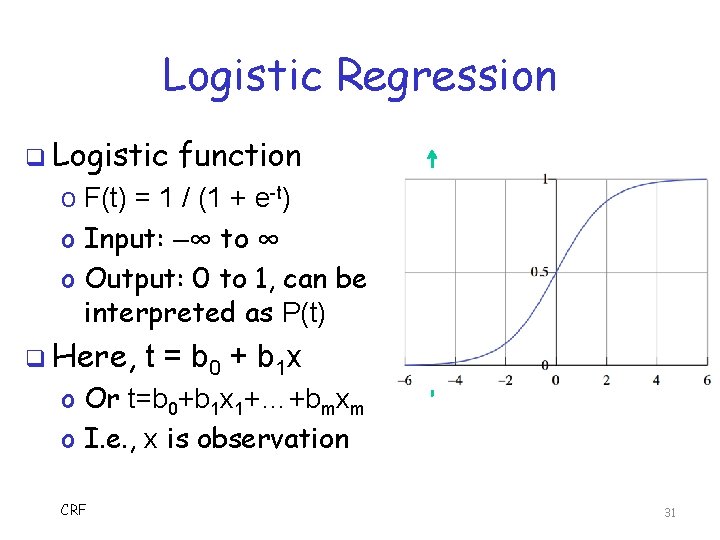
Logistic Regression q Logistic function o F(t) = 1 / (1 + e-t) o Input: –∞ to ∞ o Output: 0 to 1, can be interpreted as P(t) q Here, t = b 0 + b 1 x o Or t=b 0+b 1 x 1+…+bmxm o I. e. , x is observation CRF 31

Logistic Regression q Instead of fitting a line to data… o Fit logistic function to data q And instead of least squares error… o Measure “deviance” distance from ideal case (where ideal is “saturated model”) q Iterative process to find parameters o Find best fit F(t) using data points o More complex training than linear case… o …but, better suited to binary classification CRF 32

Conditional Probability q Recall, we would like to model P(X, O) o Observe that P(X, O) includes all relationships between Xs and Os o Too complex, too many parameters… q So we settle for P(X|O) o A lot fewer parameters o Problem is tractable o Works well in practice CRF 33

Generative vs Discriminative q We are interested in P(X|O) q Generative models o Focus on P(O|X) P(X) o From Naïve Bayes (without denominator) q Discriminative models o Focus directly on P(X|O) o Like logistic regression q Tradeoffs? CRF 34

Generative vs Discriminative q Naïve Bayes is generative model o Since it uses P(O|X) P(X) o Good in unsupervised case, unlabeled data q Logistic o o CRF regression is discriminative Directly deal with P(X|O) No need to expend effort modeling O So, more freedom to model X Unsupervised is “active area of research” 35

HMM and Naïve Bayes q Connection(s) between NB and HMM? q Recall HMM, problem 2 o For given O, find “best” (hidden) state X q We use P(X|O) to determine best X q Alpha pass used in solving problem 2 q Looking closely at alpha pass… o It is based on computing P(O|X) P(X) o With probabilities from the model λ CRF 36

HMM and Naïve Bayes q Connection(s) between NB and HMM? q HMM can be viewed as sequential version of Naïve Bayes o Classifications over series of observations o HMM uses info about state transitions q Conversely, Naïve Bayes is a “static” version of HMM q Bottom line: HMM is generative model CRF 37

CRF and Logistic Regression q Connection between CRF & regression? q Linear chain CRF is sequential version of logistic regression o Classification over series of observations o CRF uses info about state transitions q Conversely, logistic regression can be viewed as static (linear chain) CRF q Bottom line: CRF discriminative model CRF 38

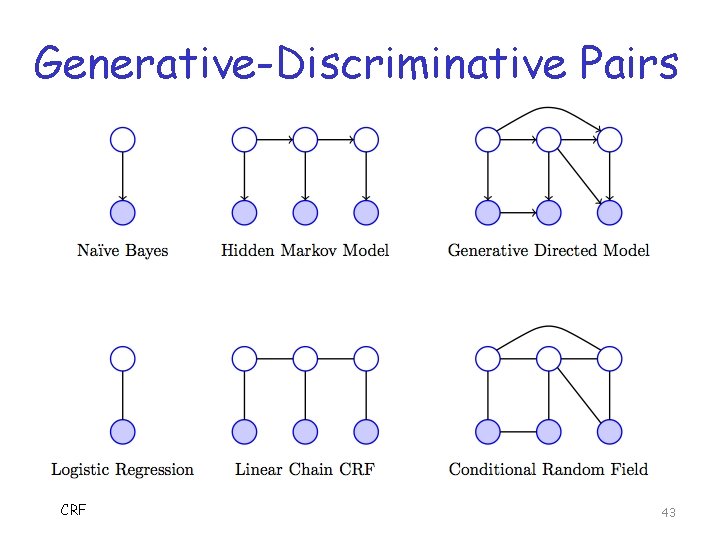
Generative vs Discriminative q Naïve Bayes and Logistic Regression o A “generative-discriminative pair” q HMM and (Linear Chain) CRF o Another generative-discriminative pair o Sequential versions of those above q Are there other such pairs? o Yes, based on further generalizations o What’s more general than sequential? CRF 39

General CRF q Can define CRF on any (undirected) graph structure o Not just a linear chain q In general CRF, training and scoring not as efficient, so… o Linear Chain CRF used most in practice q If special cases, might be worth considering more general CRF 40

Generative Directed Model q Can view HMM as defined on (directed) line graph q Could consider similar process on more general (directed) graph structures q This more general case is known as “generative directed model” q Algorithms (training, scoring, etc. ) not as efficient in more general case CRF 41

Generative-Discriminative Pair q Generative directed model o As the name implies, a generative model q General CRF o A discriminative model q So, this gives us a 3 rd generativediscriminative pair q Summary on next slide… CRF 42

Generative-Discriminative Pairs CRF 43

HCRF q Yes, you guessed it… o Hidden Conditional Random Field q So, what is hidden? q To be continued… CRF 44

Algorithms q Where are the algorithms? o This is a CS class, after all… q Yes, CRF algorithms do exist o Omitted, since lot of background needed o Would take too long to cover it all o We’ve got better things to do q So, just use existing implementations o It’s your lucky day… CRF 45

References E. Chen, Introduction to conditional random fields q Y. Ko, Maximum entropy Markov models and conditional random fields q A. Quattoni, Tutorial on conditional random fields for sequence prediction q CRF 46

References C. Sutton and A. Mc. Callum, An introduction to conditional random fields, Foundations and Trends in Machine Learning, 4(4): 267 -373, 2011 q H. M. Wallach, Conditional random fields: An introduction, 2004 q CRF 47