Conditional Probability Independent Events Finite 7 5 example

Conditional Probability: Independent Events Finite 7 -5

example: • Toss a balanced die once and record the number on the top face. • Let E be the event that a 1 shows on the top face. • Let F be the event that the number on the top face is odd. – What is P(E)? – What is the Probability of the event E if we are told that the number on the top face is odd, that is, we know that the event F has occurred? Conditional Probability

• Key idea: The original sample space no longer applies. • The new or reduced sample space is S={1, 3, 5} • Notice that the new sample space consists only of the outcomes in F. • P(E occurs given that F occurs) = 1/3 • Notation: P(E|F) = 1/3 Conditional Probability

• Def. The conditional probability of E given F is the probability that an event, E, will occur given that another event, F, has occurred if Conditional Probability
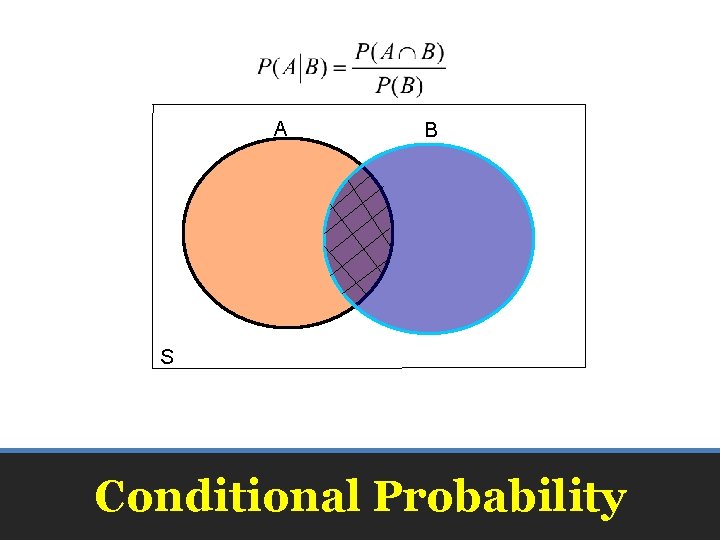
A B S Conditional Probability

• If the outcomes of an experiment are equally likely, then Conditional Probability

• Example: Earned degrees in the United States in recent year Conditional Probability

The academy awards is soon to be shown. For a specific married couple the probability that the husband watches the show is 80%, the probability that his wife watches the show is 65%, while the probability that they both watch the show is 60%. If the husband is watching the show, what is the probability that his wife is also watching the show Example

The academy awards is soon to be shown. Let B = the event that the husband watches the show P[B]= 0. 80 Let A = the event that his wife watches the show P[A]= 0. 65 and P[A ∩ B]= 0. 60 Example

Conditional Probability can be rewritten as follows Conditional Probability

Example: E: dollar falls in value against the yen F: supplier demands renegotiation of contract Find Conditional Probability

mutually exclusive Two mutually exclusive events are independent only in the special case where A B Mutually exclusive events are highly dependent otherwise. A and B cannot occur simultaneously. If one event occurs the other event does not occur. Difference between independence and mutually exclusive

or S A B The ratio of the probability of the set A within B is the same as the ratio of the probability of the set A within the entire sample S. Difference between independence and mutually exclusive

and if A and B are independent. The multiplicative rule of probability

If the probability of the occurrence of event A is the same regardless of whether or not an outcome B occurs, then the outcomes A and B are said to be independent of one another. Symbolically, if then A and B are independent events. Independent Events

then we can also state the following relationship for independent events: if and only if A and B are independent events. Independent Events

• A coin is tossed and a single 6 -sided die is rolled. Find the probability of getting a head on the coin and a 3 on the die. • Probabilities: P(head) = 1/2 P(3) = 1/6 P(head and 3) = 1/2 * 1/6 = 1/12 Example

• Example: If E, F, and G are independent, then Independence Formula – 3 events

• If E, F, and G are independent given that an event H has occurred, then The Notion of Independence applied to Conditional Probability

• Independent Events vs. Mutually Exclusive Events (Disjoint Events) • If two events are Independent, • If two events are Mutually Exclusive Events then they do not share common outcomes Important

Summary of the Rules of Probability
![P[A B] = P[A] + P[B] – P[A B] and P[A B] = P[A] P[A B] = P[A] + P[B] – P[A B] and P[A B] = P[A]](http://slidetodoc.com/presentation_image_h2/98f6ded8e05528b4b9f248b4d2e68584/image-22.jpg)
P[A B] = P[A] + P[B] – P[A B] and P[A B] = P[A] + P[B] if P[A B] = f The Additive Rule

for any event E The Rule for Complements

Conditional probability

and if A and B are independent. This is the definition of independent The multiplicative rule of probability

• you have a box with 3 blue marbles, 2 red marbles, and 4 yellow marbles. You are going to pull out one marble, record its color, put it back in the box and draw another marble. What is the probability of pulling out a red marble followed by a blue marble? Example

• you have a box with 3 blue marbles, 2 red marbles, and 4 yellow marbles. You are going to pull out one marble, record its color, put it back in the box and draw another marble. What is the probability of pulling out a red marble followed by a blue marble? Example

• Suppose you are going to draw two cards from a standard deck. What is the probability that the first card is an ace and the second card is a jack (just one of several ways to get “blackjack” or 21). Example

• Suppose you are going to draw two cards from a standard deck. What is the probability that the first card is an ace and the second card is a jack (just one of several ways to get “blackjack” or 21). Example

• Pages 330 – 333 • 1 -15 odd, 21, 23, 29, 33 – 43 odd, 49 – 53 all, 64 – 67 all, 73 Homework
- Slides: 30