Conditional Probability and Independence Section 3 6 Definition

Conditional Probability and Independence Section 3. 6

Definition • A conditional probability is a probability whose sample space has been limited to only those outcomes that fulfill a certain condition. • The conditional probability of event A given that event B has happened is P(A|B)=P(A ∩ B)/P(B). • The order is very important do not think that P(A|B)=P(B|A)! THEY ARE DIFFERENT.

Exercise #1 • Suppose that A and B are events with probabilities: P(A)=1/3, P(B)=1/4, P(A ∩ B)=1/10 • Find each of the following: 1. P(A | B) = P(A ∩ B)/P(B)=1/10/1/4=4/10 2. P(B | A) = P(A ∩ B)/P(A)=1/10/1/3=3/10 3. P(A’ | B’) = P(A’ ∩ B’)/P(B’)= P((A U B)’)/(1 -P(B))=(1 -P(A U B))/(1 – P(B))= (1 – (P(A)+P(B)-P(A ∩ B)))/(1 -P(B))= (1 – (1/3+1/4 -1/10))/(1 -1/10)=(1 -29/60)/9/10= 31/60/9/10=31/54.

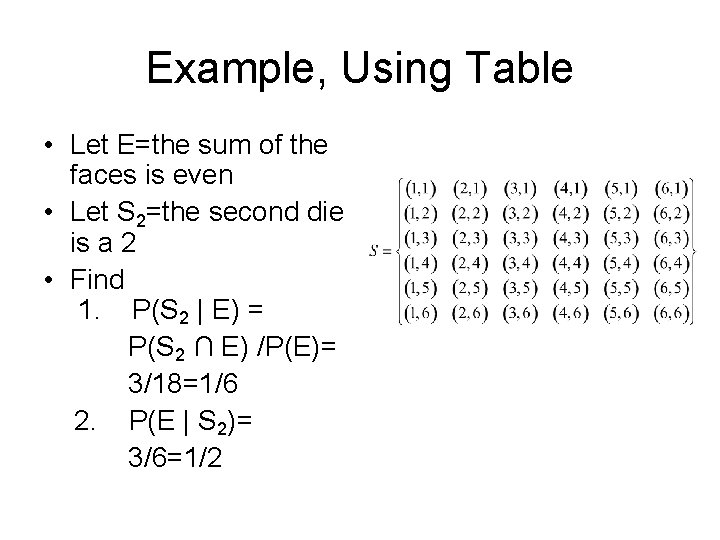
Example, Using Table • Let E=the sum of the faces is even • Let S 2=the second die is a 2 • Find 1. P(S 2 | E) = P(S 2 ∩ E) /P(E)= 3/18=1/6 2. P(E | S 2)= 3/6=1/2

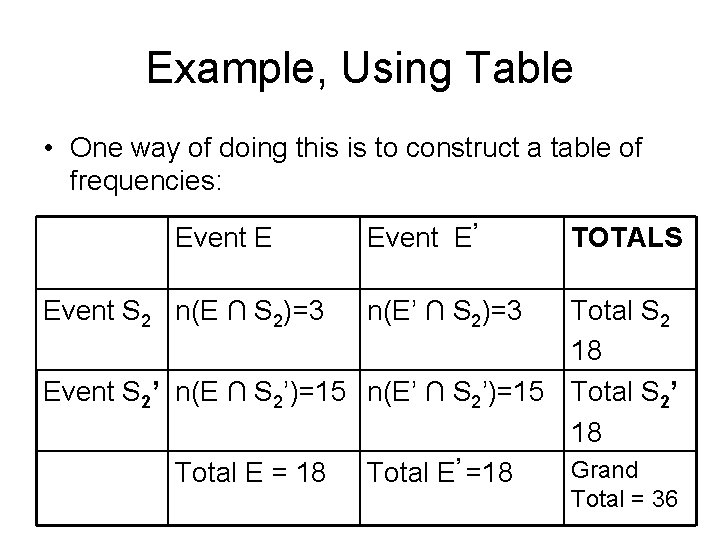
Example, Using Table • One way of doing this is to construct a table of frequencies: Event E Event S 2 n(E ∩ S 2)=3 Event E’ TOTALS n(E’ ∩ S 2)=3 Total S 2 18 Event S 2’ n(E ∩ S 2’)=15 n(E’ ∩ S 2’)=15 Total S 2’ 18 Grand Total E = 18 Total E’ =18 Total = 36

Independence of events • Two events E and F are said to be independent if and only if P(E ∩ F)=P(E)P(F). • If the above condition is not satisfied, then we say the two events E and F are dependent. • When we say two events are independent, we are saying that if event E has occurred, this will not effect the probability of event F. • INDEPENDENT EVENTS: The occurrence of one event has no effect on the probability of the other.

Independent Events • Consider flipping a coin recording the outcome each time. Are these events independent? ? • You throw 2 fair dice, one is green, one is red. Observe the outcomes. • Let A be the event that the sum is 7 • Let B be the event that the red die shows an even number • Are A and B Independent? • Are A and B Mutually exclusive?