Condensed Matter Physics review 1 Free Electron Gas

Condensed Matter Physics: review 1

Free Electron Gas in Metals l l l Solid metals are bonded by the metallic bond One or two of the valence electrons from each atom are free to move throughout the solid All atoms share all the electrons. A metal is a lattice of positive ions immersed in a gas of electrons. The binding between the electrons and the lattice is what holds the solid together 2

Fermi-Dirac “Filling” Function Probability of electrons to be found at various energy levels. • For E – EF = 0. 05 e. V f(E) = 0. 12 For E – EF = 7. 5 e. V f(E) = 10 – 129 • Exponential dependence has HUGE effect! • Temperature dependence of Fermi-Dirac function shown as follows: 3

Free Electron Gas in Metals Since we are dealing with fermions, the electron gas obeys Fermi-Dirac statistics. The number of electrons with energy in the range E to E+d. E is given by where, the density of states g(E) is given by 4

Free Electron Gas in Metals The electron has two spin states, so W = 2. If the electron’s speed << c, we can take its energy to be So the number of states in (E, E+d. E) is given by 5

Free Electron Gas in Metals The number of electrons in the interval E to E+d. E is therefore The first term is the Fermi-Dirac distribution and the second is the density of states g(E)d. E 6

Free Electron Gas in Metals From n(E) d. E we can calculate many global characteristics of the electron gas. Here are just a few l The Fermi energy – the maximum energy level occupied by the free electrons at absolute zero l l The average energy The total number of electrons in the electron gas 7

Free Electron Gas in Metals The total number of electrons N is given by the integral At T=0, the Fermi-Dirac distribution is equal to 1 if E < EF and 0 if E > EF. At T=0, all energy levels are filled up to the energy EF, called the Fermi energy. 8

Free Electron Gas in Metals The total number of electrons N is given by The average energy of a free electron is given by 9

Free Electron Gas in Metals At T = 0, the integrals are easy to do. For example, the total number of electrons is 10

Free Electron Gas in Metals The average energy of an electron is This implies EF = k TF defines the Fermi temperature 11

Summary of metallic state l l The ions in solids form regular lattices A metal is a lattice of positive ions immersed in a gas of electrons. All ions share all electrons The attraction between the electrons and the lattice is called a metallic bond At T = 0, all energy levels up to the Fermi energy are filled 12

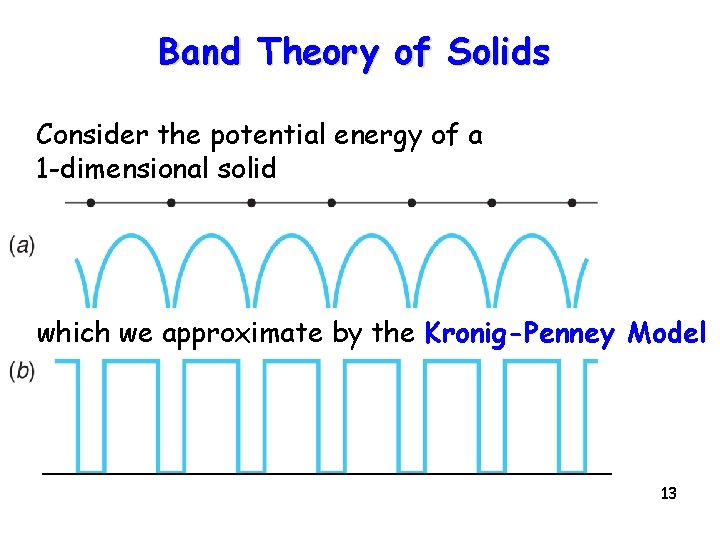
Band Theory of Solids Consider the potential energy of a 1 -dimensional solid which we approximate by the Kronig-Penney Model 13

Band Theory of Solids The task is to compute the quantum states and associated energy levels of this simplified model by solving the Schrödinger equation 1 2 3 14

Band Theory of Solids For periodic potentials, Felix Bloch showed that the solution of the Schrödinger equation must be of the form and the wavefunction must reflect the periodicity of the lattice: 1 2 3 15

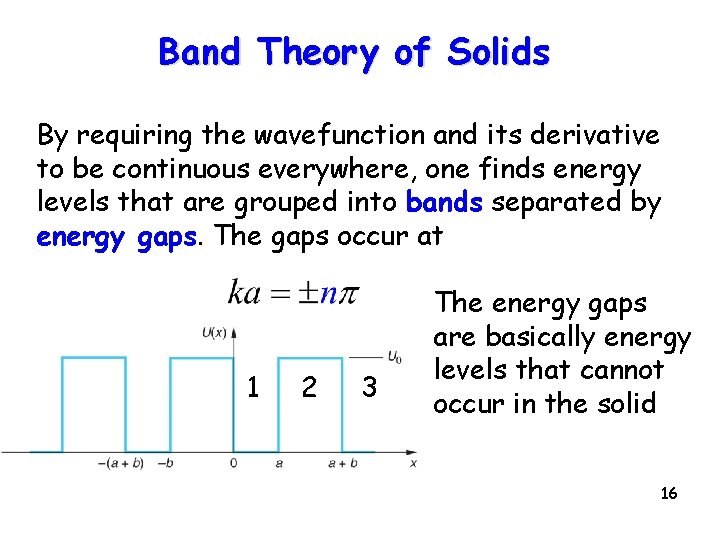
Band Theory of Solids By requiring the wavefunction and its derivative to be continuous everywhere, one finds energy levels that are grouped into bands separated by energy gaps. The gaps occur at 1 2 3 The energy gaps are basically energy levels that cannot occur in the solid 16

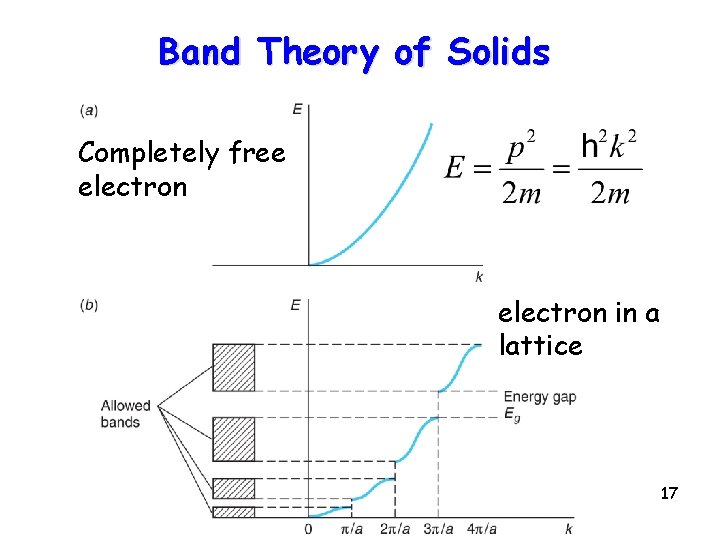
Band Theory of Solids Completely free electron in a lattice 17

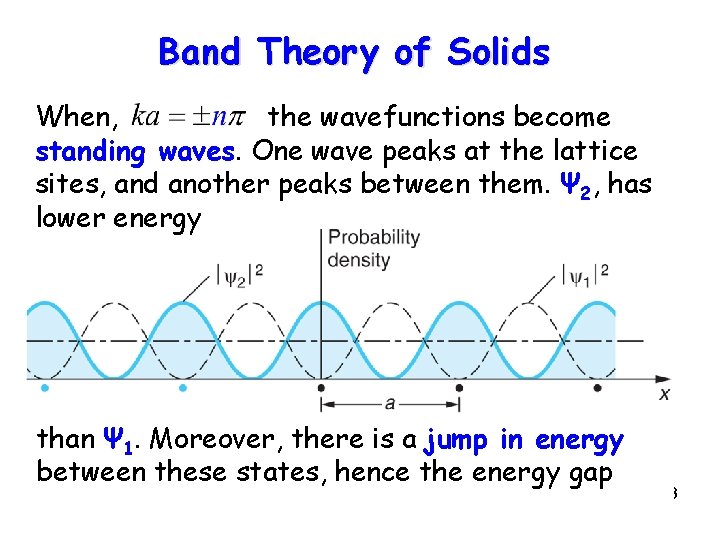
Band Theory of Solids When, the wavefunctions become standing waves. One wave peaks at the lattice sites, and another peaks between them. Ψ 2, has lower energy than Ψ 1. Moreover, there is a jump in energy between these states, hence the energy gap 18

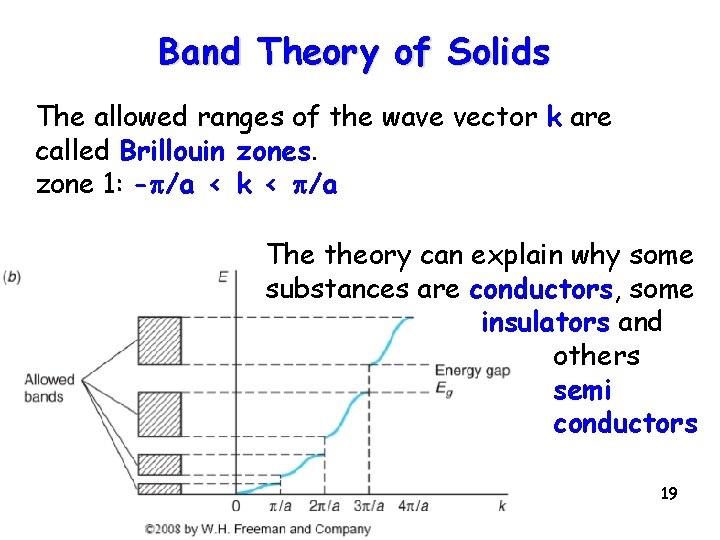
Band Theory of Solids The allowed ranges of the wave vector k are called Brillouin zones. zone 1: -p/a < k < p/a The theory can explain why some substances are conductors, some insulators and others semi conductors 19