Concurrent Reconfiguration of Hexagonal Metamorphic Robots Algorithms for

Concurrent Reconfiguration of Hexagonal Metamorphic Robots: Algorithms for Fast Execution and Obstacle Envelopment Elizabeth M. Tsai Swarthmore College USRG 2002 Jennifer E. Walter Vassar College Nancy M. Amato Texas A&M University
Metamorphic Robotic Systems What are metamorphic robots? • robots with the capability to change shape • i. e. Transformers What are Transformers? • fighting robots that transform into everyday objects (e. g. cars, planes, appliances) Sunstreaker Soundwave USRG 2002

Transformer Background Two types of transformers… 1) Autobots USRG 2002 2) Decepticons • “good guys” • “bad guys” • lead by Optimus Prime • lead by Megatron
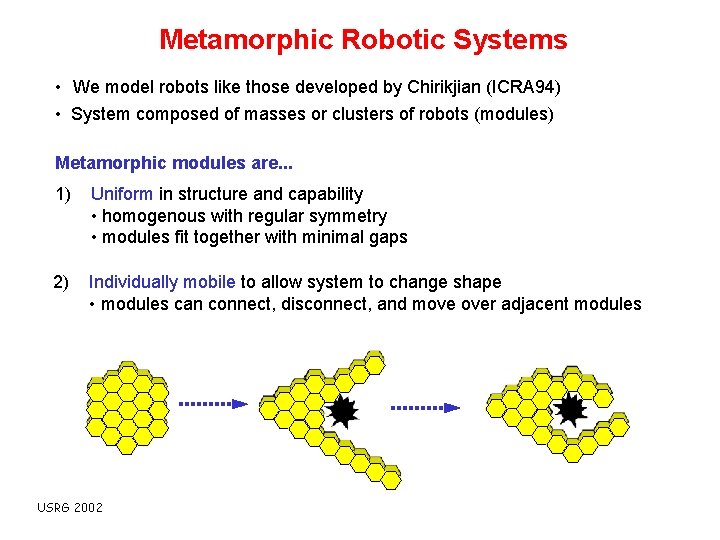
Metamorphic Robotic Systems • We model robots like those developed by Chirikjian (ICRA 94) • System composed of masses or clusters of robots (modules) Metamorphic modules are. . . 1) Uniform in structure and capability • homogenous with regular symmetry • modules fit together with minimal gaps 2) Individually mobile to allow system to change shape • modules can connect, disconnect, and move over adjacent modules USRG 2002
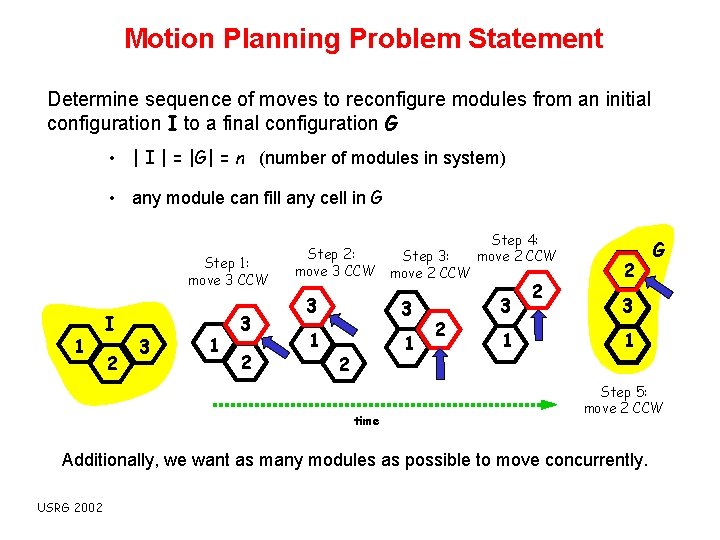
Motion Planning Problem Statement Determine sequence of moves to reconfigure modules from an initial configuration I to a final configuration G • | I | = |G| = n (number of modules in system) • any module can fill any cell in G Step 1: move 3 CCW 1 I 2 3 1 3 2 Step 4: Step 2: Step 3: move 2 CCW move 3 CCW move 2 CCW 3 3 1 1 2 time 2 3 1 2 2 3 1 Step 5: move 2 CCW Additionally, we want as many modules as possible to move concurrently. USRG 2002 G
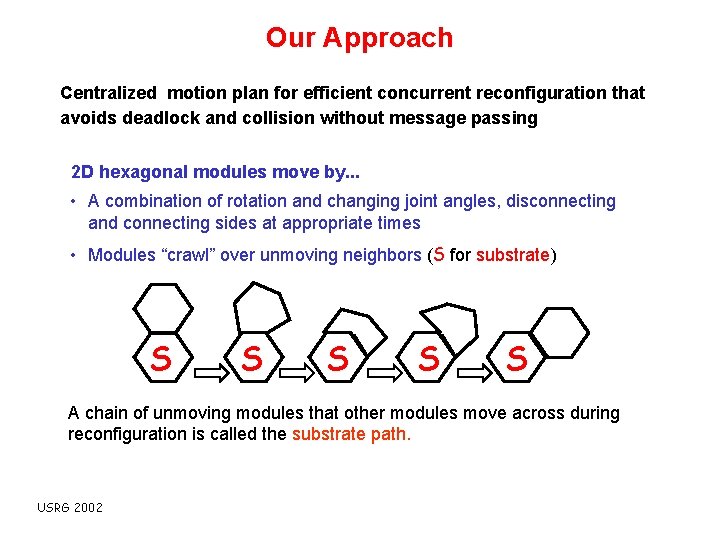
Our Approach Centralized motion plan for efficient concurrent reconfiguration that avoids deadlock and collision without message passing 2 D hexagonal modules move by. . . • A combination of rotation and changing joint angles, disconnecting and connecting sides at appropriate times • Modules “crawl” over unmoving neighbors (S for substrate) S S S A chain of unmoving modules that other modules move across during reconfiguration is called the substrate path. USRG 2002
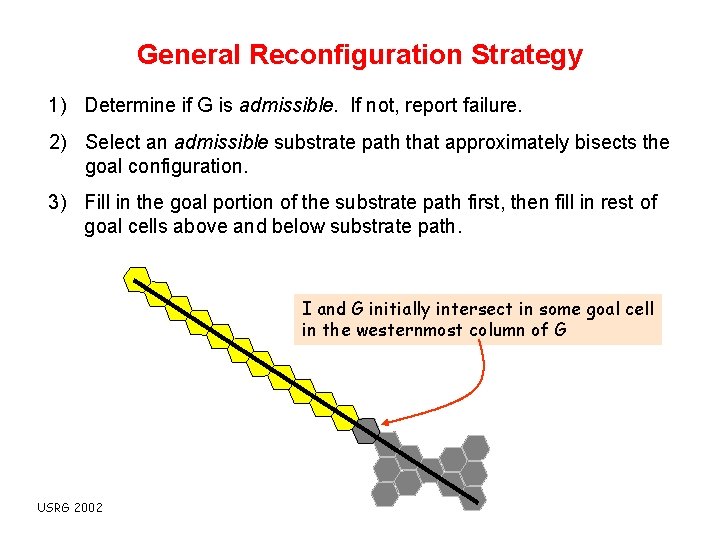
General Reconfiguration Strategy 1) Determine if G is admissible. If not, report failure. 2) Select an admissible substrate path that approximately bisects the goal configuration. 3) Fill in the goal portion of the substrate path first, then fill in rest of goal cells above and below substrate path. I and G initially intersect in some goal cell in the westernmost column of G USRG 2002
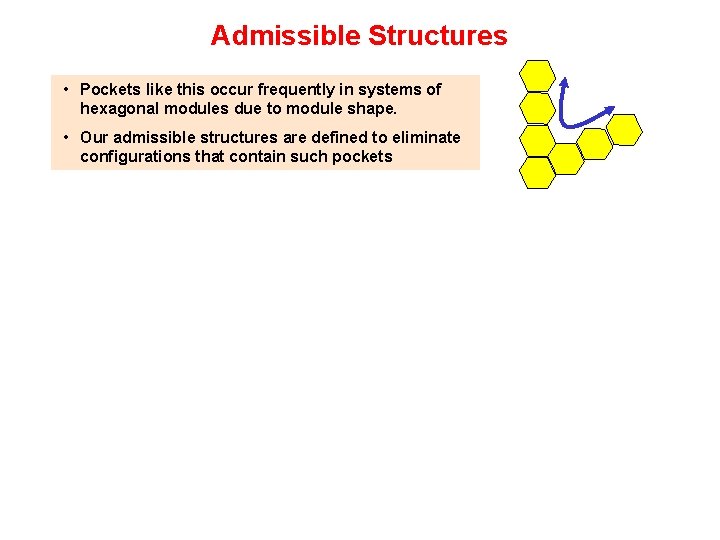
Admissible Structures • Pockets like this occur frequently in systems of hexagonal modules due to module shape. • Our admissible structures are defined to eliminate configurations that contain such pockets
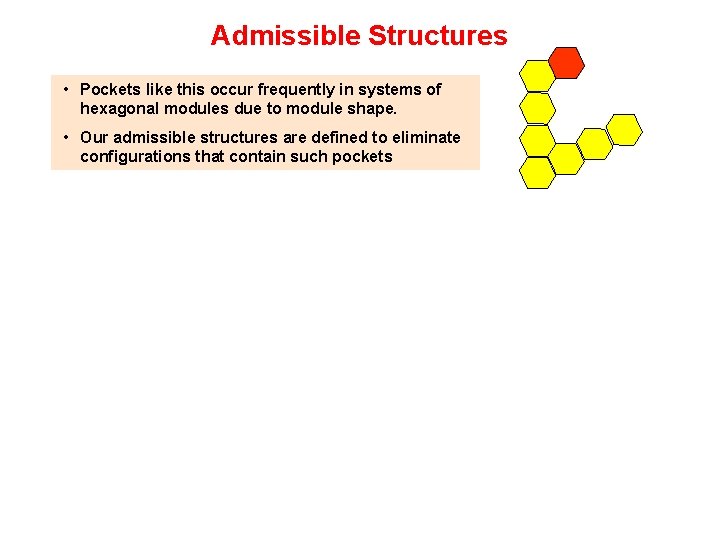
Admissible Structures • Pockets like this occur frequently in systems of hexagonal modules due to module shape. • Our admissible structures are defined to eliminate configurations that contain such pockets
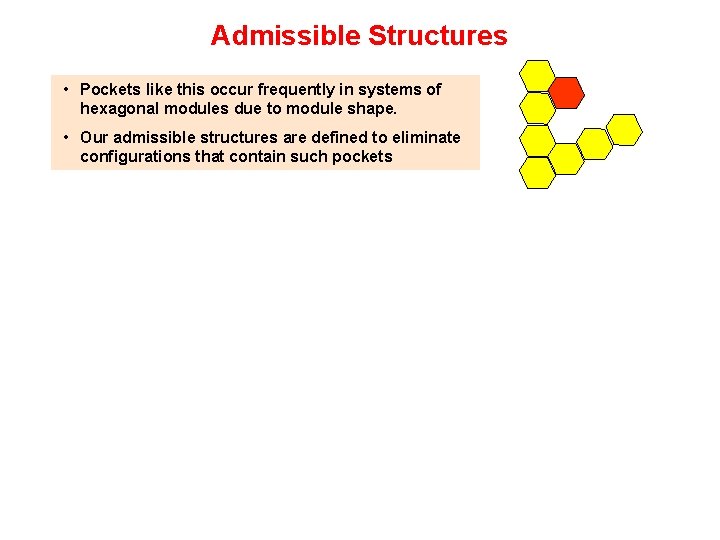
Admissible Structures • Pockets like this occur frequently in systems of hexagonal modules due to module shape. • Our admissible structures are defined to eliminate configurations that contain such pockets
Admissible Structures • Pockets like this occur frequently in systems of hexagonal modules due to module shape. • Our admissible structures are defined to eliminate configurations that contain such pockets
Admissible Structures • Pockets like this occur frequently in systems of hexagonal modules due to module shape. • Our admissible structures are defined to eliminate configurations that contain such pockets
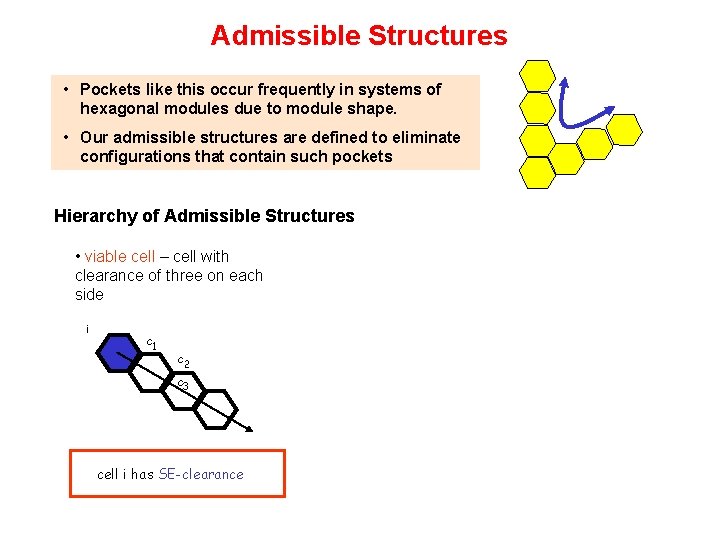
Admissible Structures • Pockets like this occur frequently in systems of hexagonal modules due to module shape. • Our admissible structures are defined to eliminate configurations that contain such pockets Hierarchy of Admissible Structures • viable cell – cell with clearance of three on each side i c 1 c 2 c 3 cell i has SE-clearance
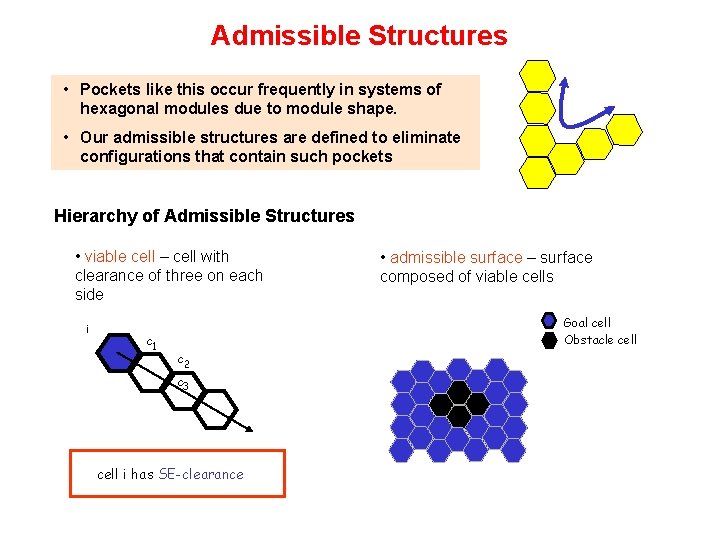
Admissible Structures • Pockets like this occur frequently in systems of hexagonal modules due to module shape. • Our admissible structures are defined to eliminate configurations that contain such pockets Hierarchy of Admissible Structures • viable cell – cell with clearance of three on each side i c 1 • admissible surface – surface composed of viable cells Goal cell Obstacle cell c 2 c 3 cell i has SE-clearance
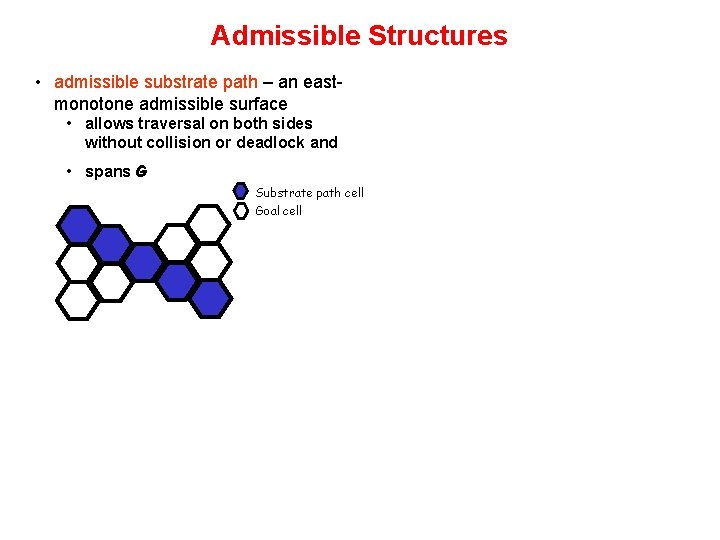
Admissible Structures • admissible substrate path – an eastmonotone admissible surface • allows traversal on both sides without collision or deadlock and • spans G Substrate path cell Goal cell
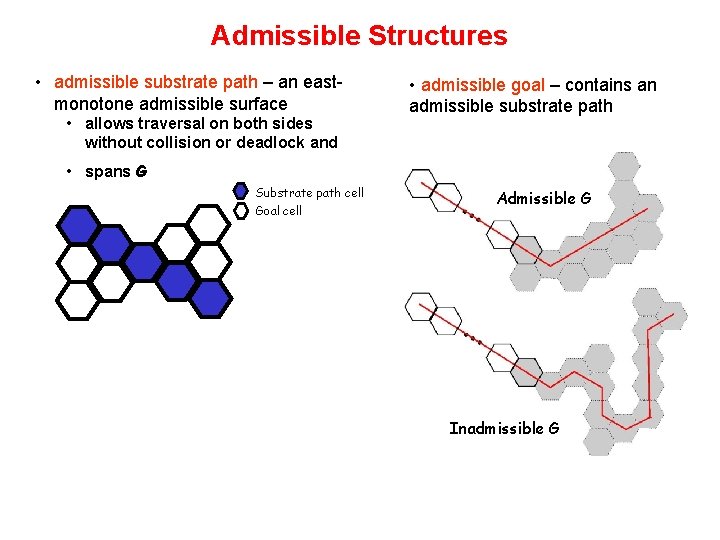
Admissible Structures • admissible substrate path – an eastmonotone admissible surface • allows traversal on both sides without collision or deadlock and • admissible goal – contains an admissible substrate path • spans G Substrate path cell Goal cell Admissible G Inadmissible G
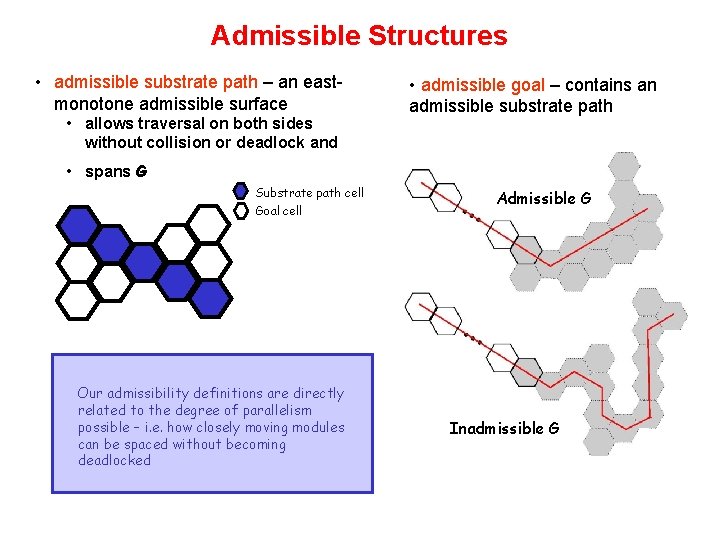
Admissible Structures • admissible substrate path – an eastmonotone admissible surface • allows traversal on both sides without collision or deadlock and • admissible goal – contains an admissible substrate path • spans G Substrate path cell Goal cell Our admissibility definitions are directly related to the degree of parallelism possible – i. e. how closely moving modules can be spaced without becoming deadlocked Admissible G Inadmissible G
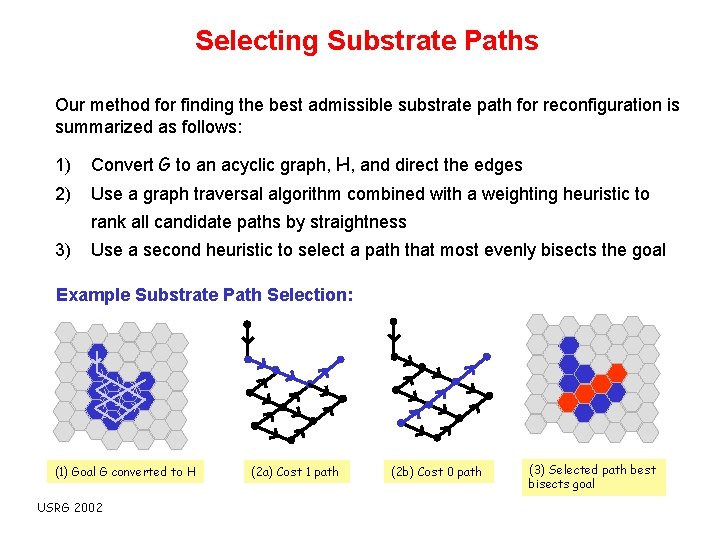
Selecting Substrate Paths Our method for finding the best admissible substrate path for reconfiguration is summarized as follows: 1) Convert G to an acyclic graph, H, and direct the edges 2) Use a graph traversal algorithm combined with a weighting heuristic to rank all candidate paths by straightness 3) Use a second heuristic to select a path that most evenly bisects the goal Example Substrate Path Selection: (1) Goal G converted to H USRG 2002 (2 a) Cost 1 path (2 b) Cost 0 path (3) Selected path best bisects goal
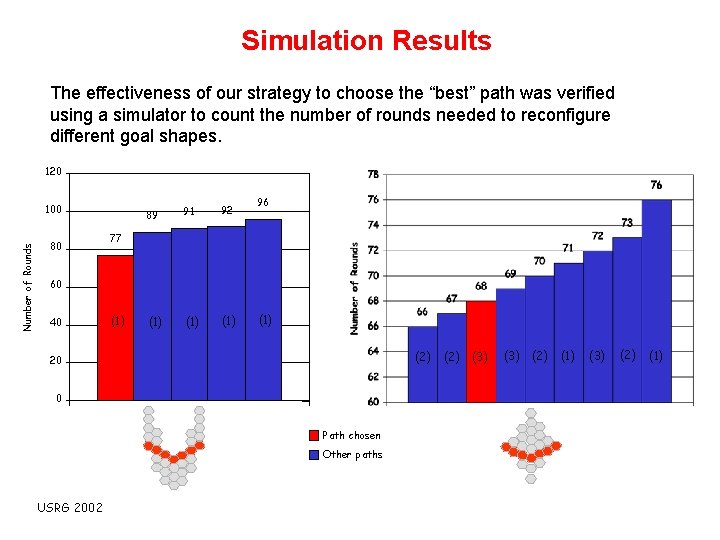
Simulation Results The effectiveness of our strategy to choose the “best” path was verified using a simulator to count the number of rounds needed to reconfigure different goal shapes. 120 Number of Rounds 100 80 89 91 92 (1) (1) 96 77 60 40 (1) (2) 20 0 Path chosen Other paths USRG 2002 (2) (3) (2) (1)
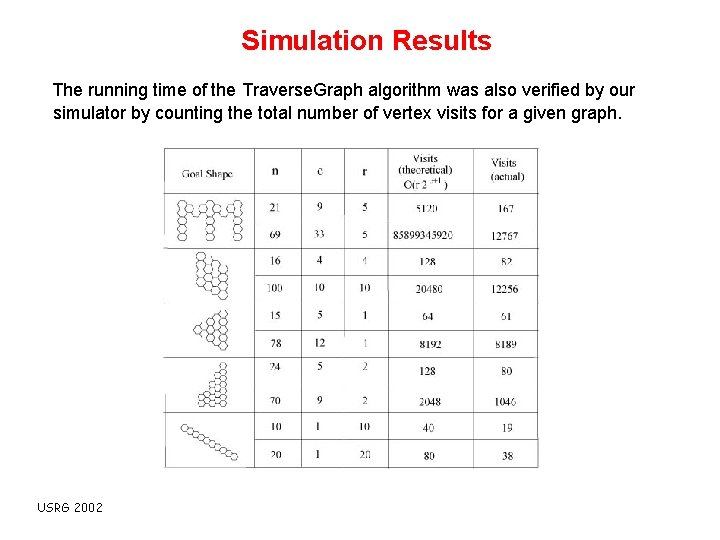
Simulation Results The running time of the Traverse. Graph algorithm was also verified by our simulator by counting the total number of vertex visits for a given graph. USRG 2002

Reconfiguration with a Single Obstacle We consider the presence of a single obstacle in the environment that must… • be enclosed completely inside the goal • be admissible • not involve purple swingy-weapons or water What is an admissible obstacle? • an obstacle that contains an admissible surface Megatron is an inadmissible obstacle How to check for obstacle admissibility For each obstacle cell on the perimeter of the obstacle… …for each side of the cell that is a goal cell… …check two and three cells over for another goal cell (i. e. pocket of size 1 or 2) USRG 2002 Obstacle with pocket of size 1

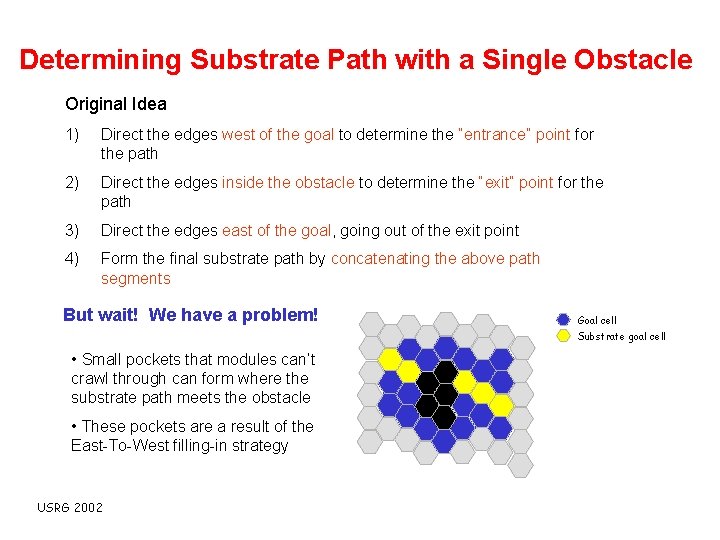
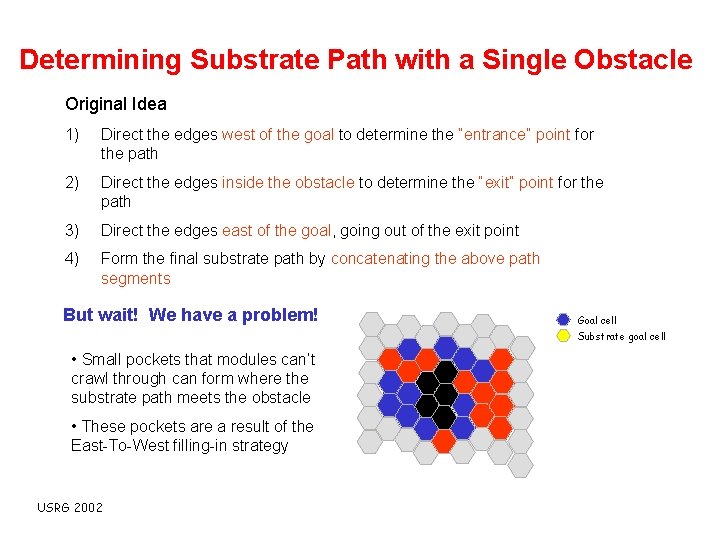
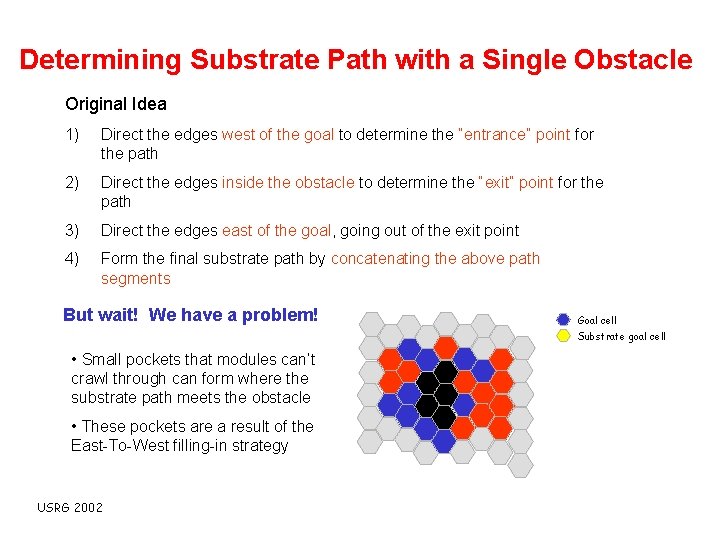
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments USRG 2002
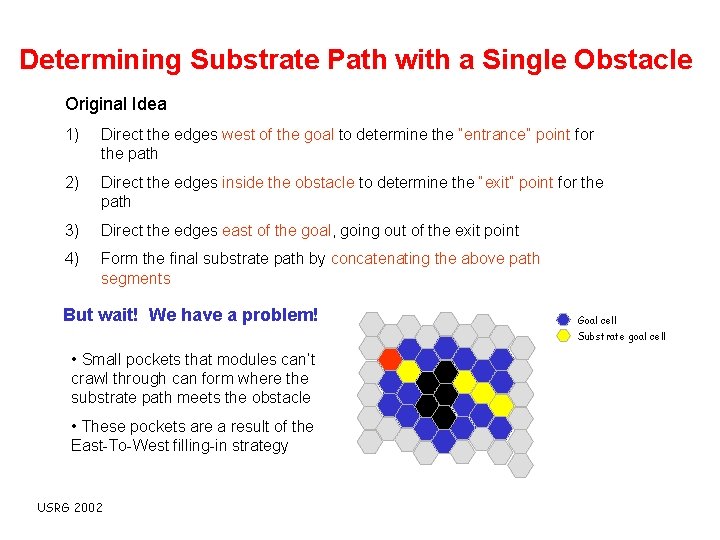
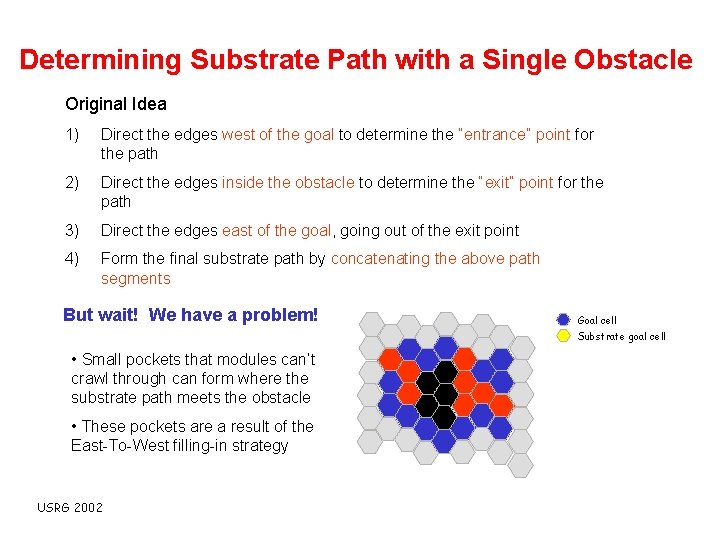
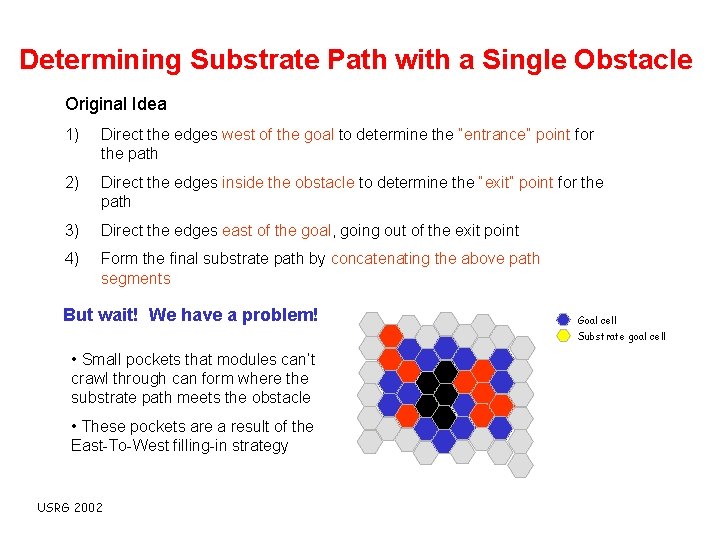
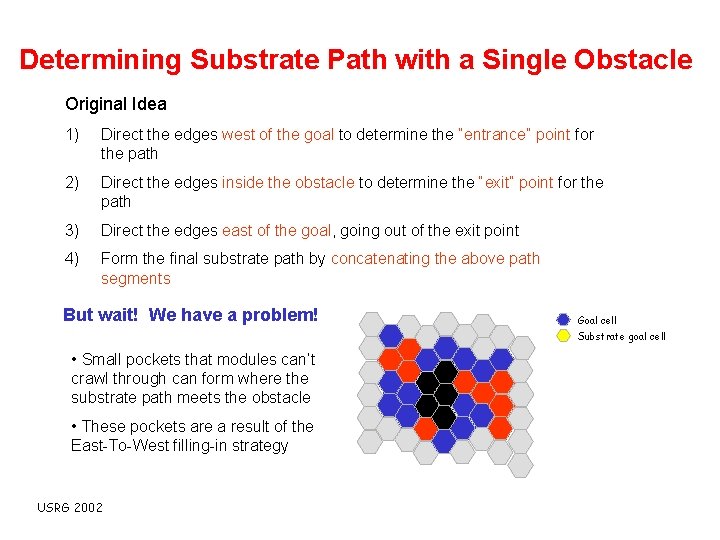
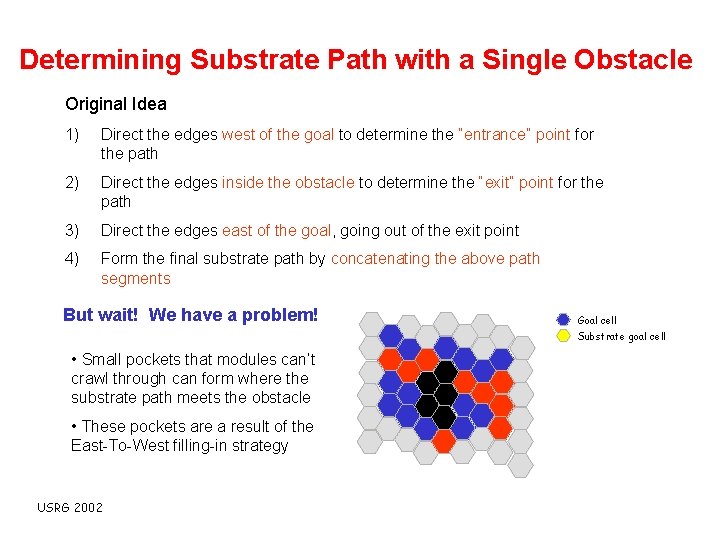
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
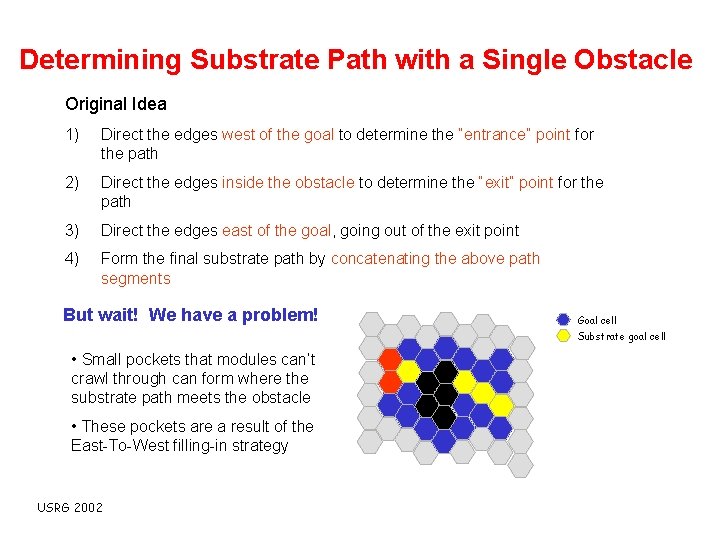
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
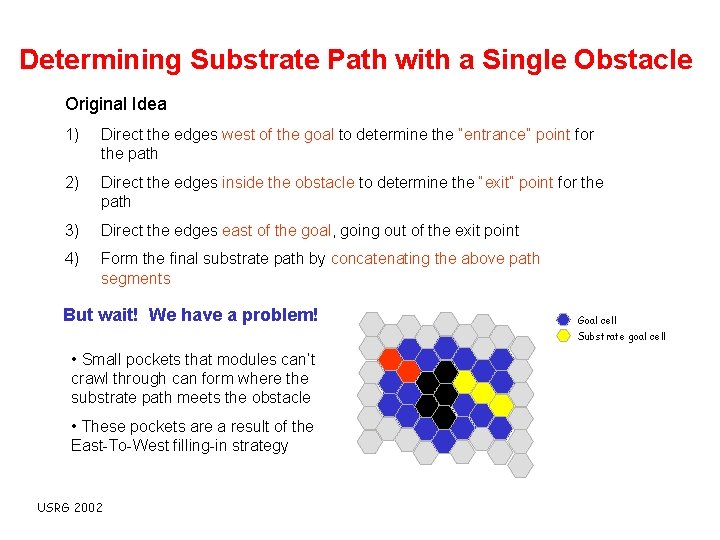
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
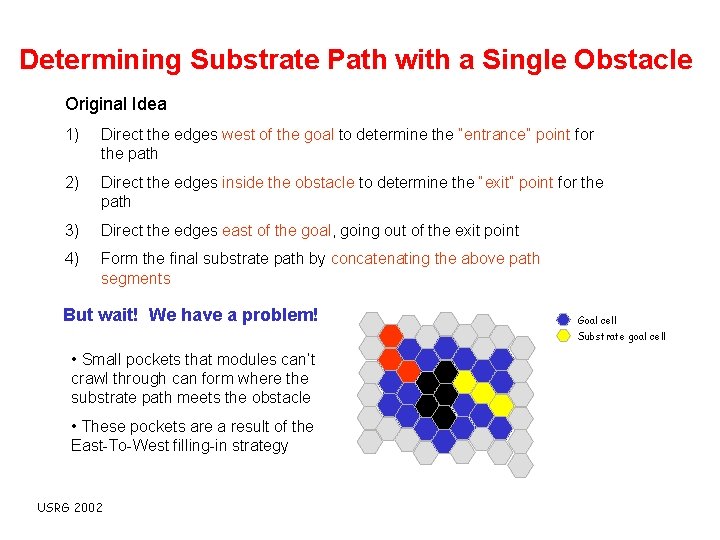
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
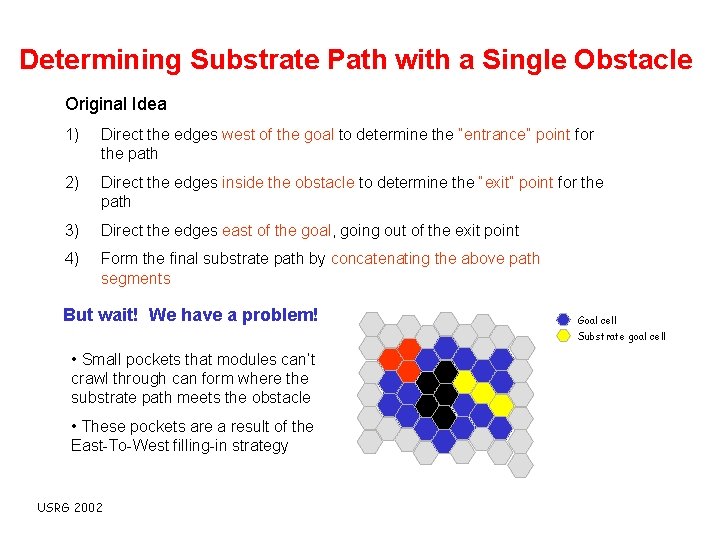
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
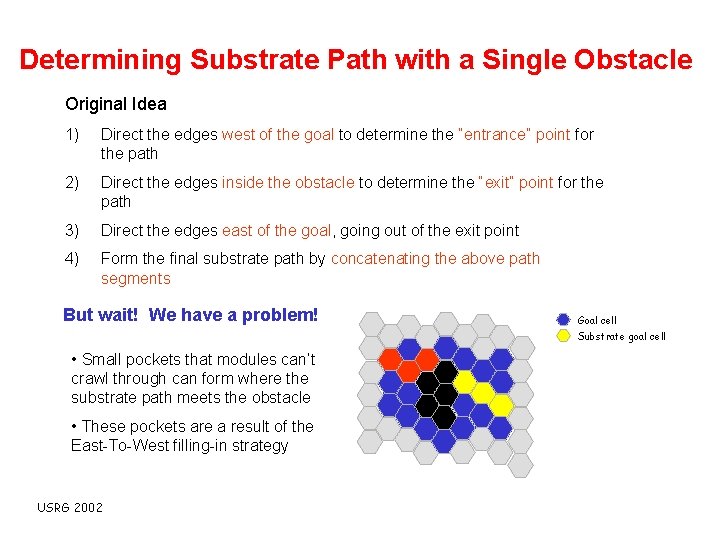
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
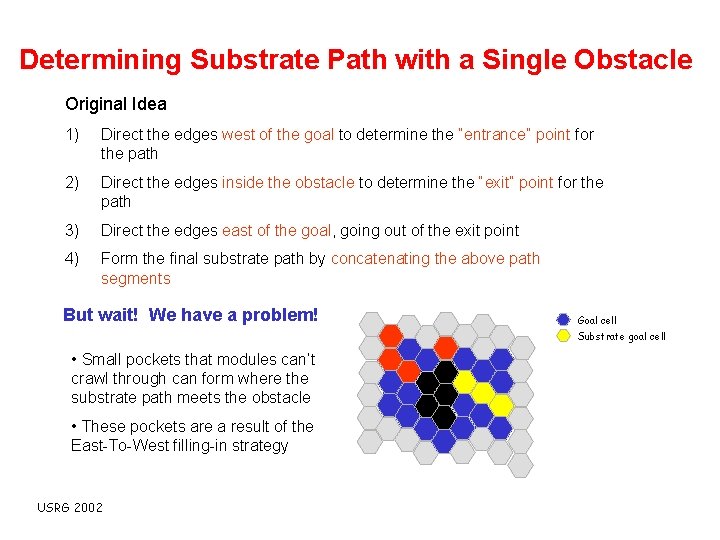
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
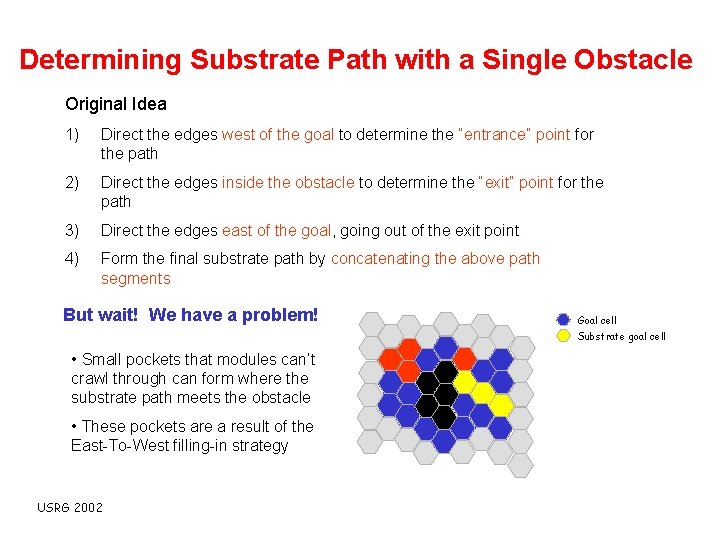
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
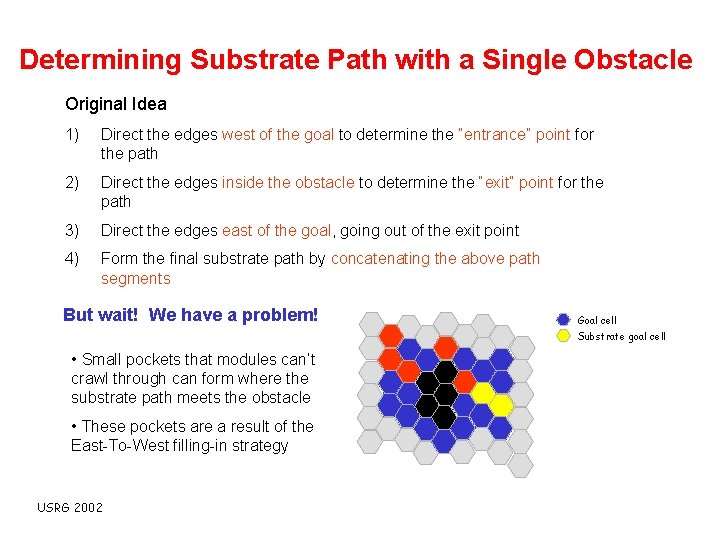
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
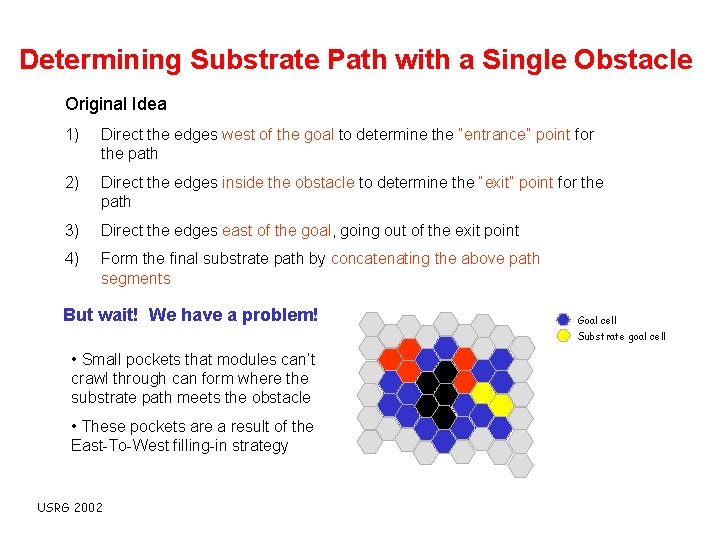
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
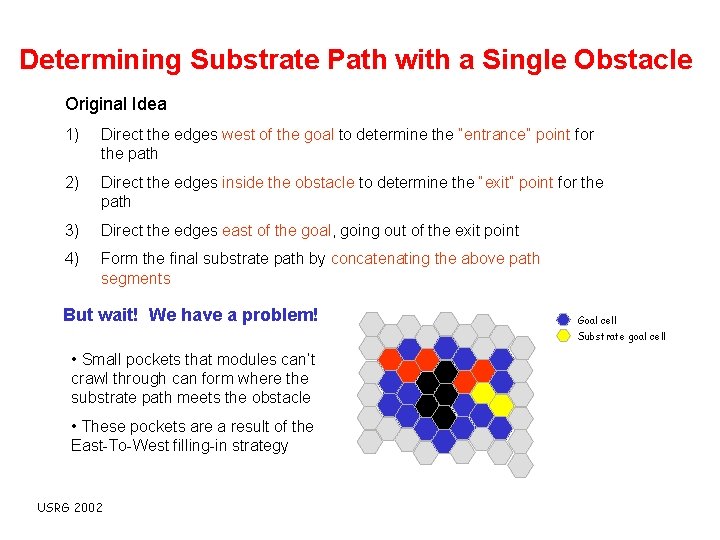
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
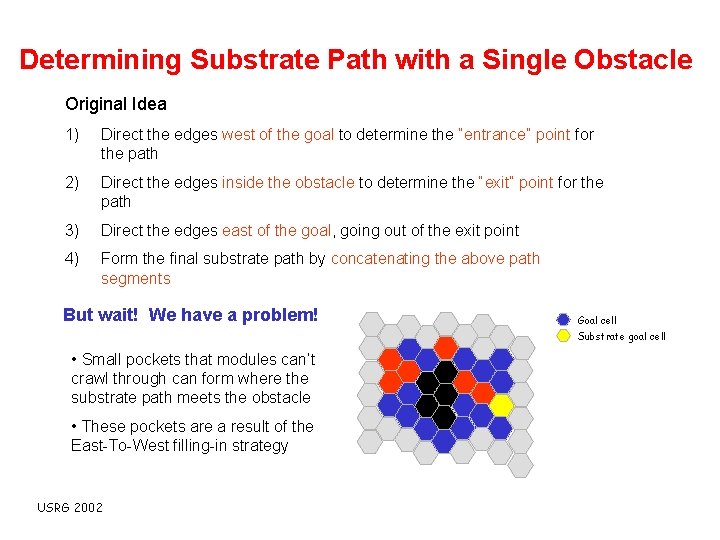
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
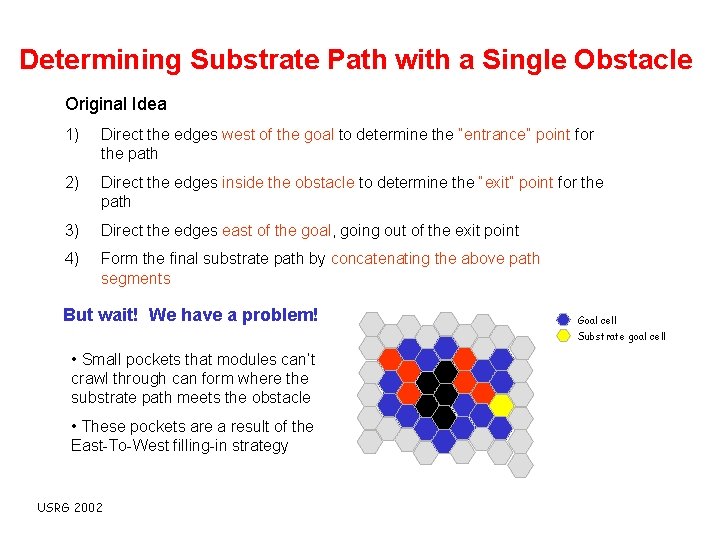
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
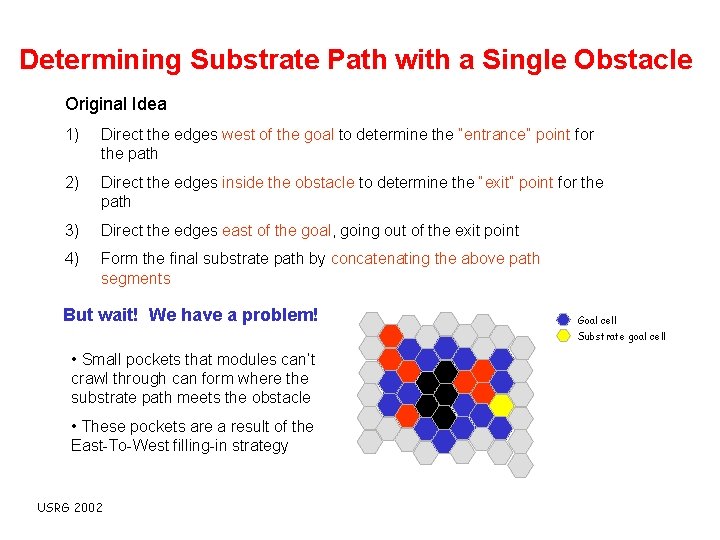
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
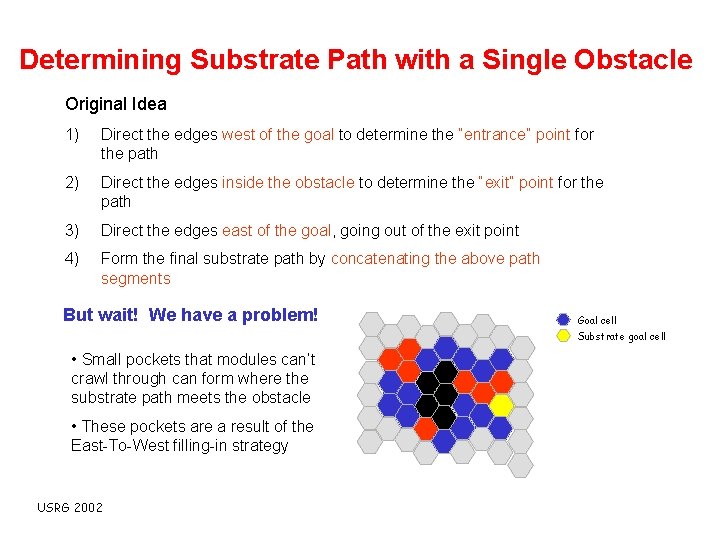
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
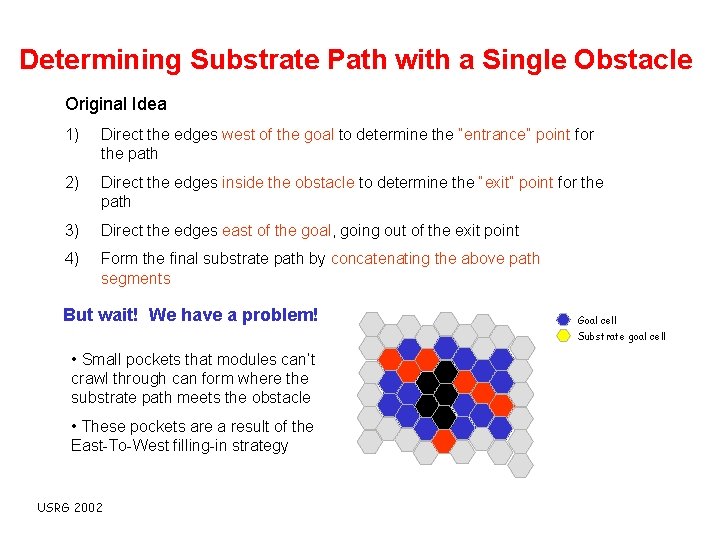
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
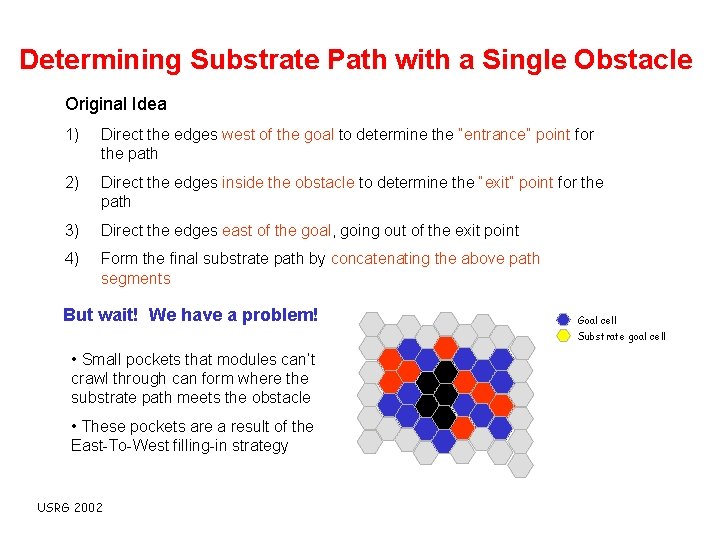
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
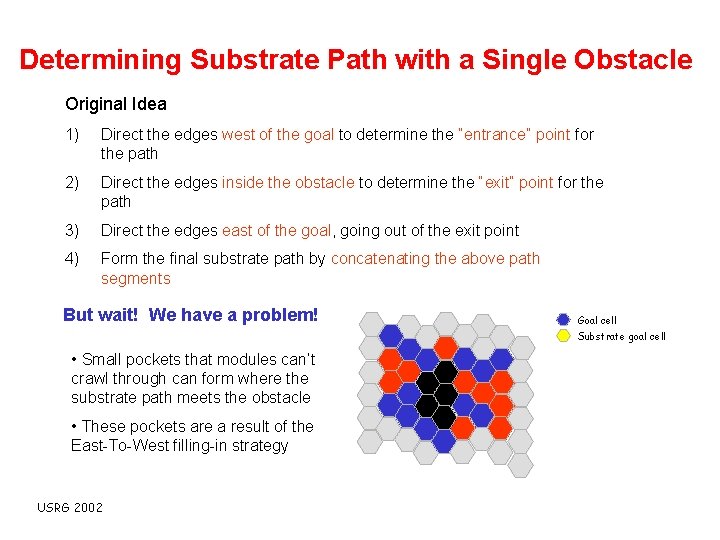
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
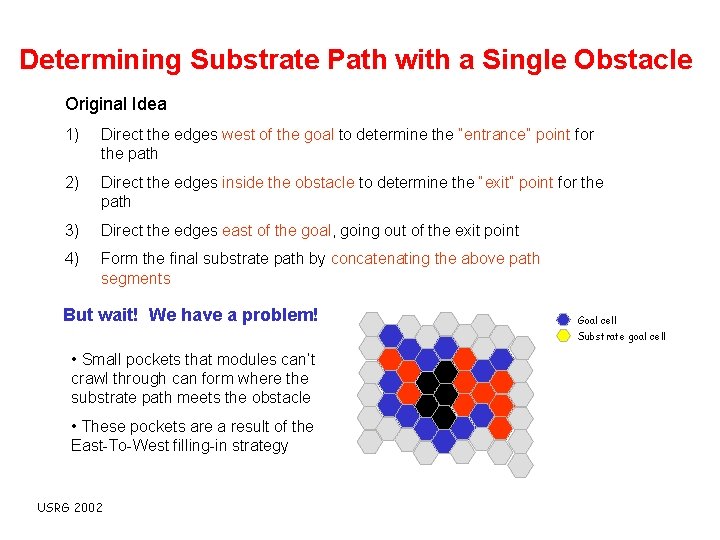
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
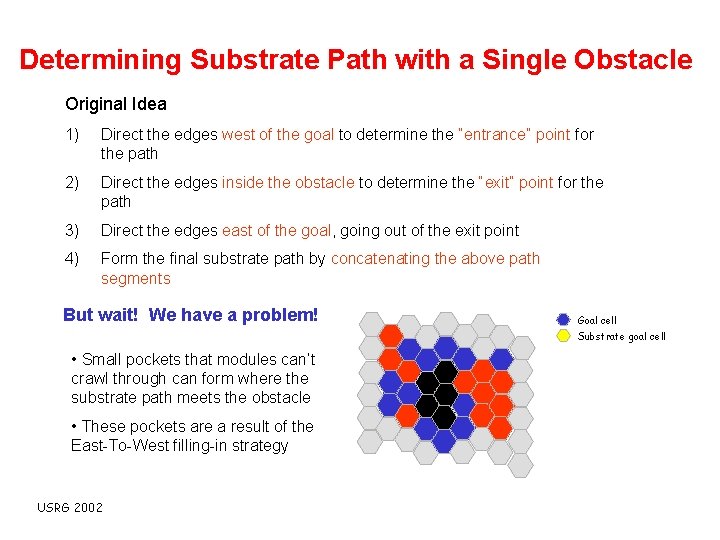
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
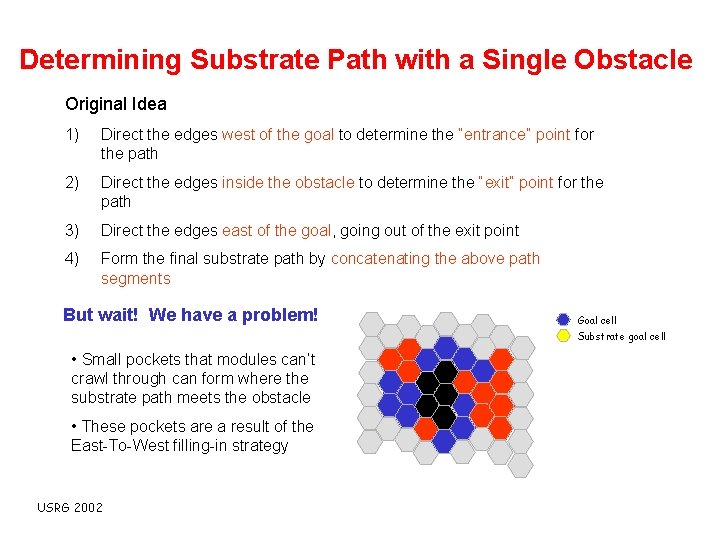
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002

Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002
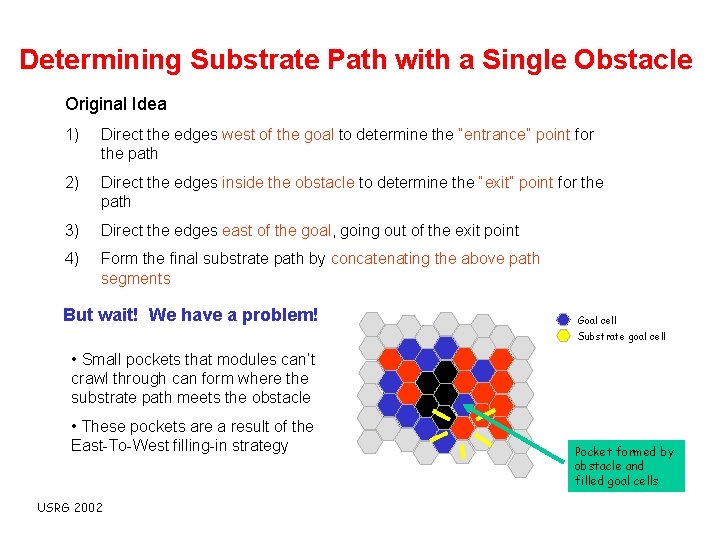
Determining Substrate Path with a Single Obstacle Original Idea 1) Direct the edges west of the goal to determine the “entrance” point for the path 2) Direct the edges inside the obstacle to determine the “exit” point for the path 3) Direct the edges east of the goal, going out of the exit point 4) Form the final substrate path by concatenating the above path segments But wait! We have a problem! Goal cell Substrate goal cell • Small pockets that modules can’t crawl through can form where the substrate path meets the obstacle • These pockets are a result of the East-To-West filling-in strategy USRG 2002 Pocket formed by obstacle and filled goal cells
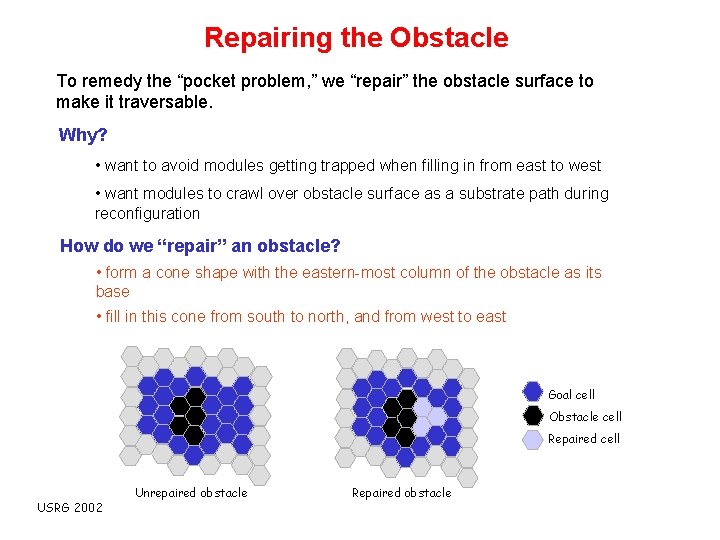
Repairing the Obstacle To remedy the “pocket problem, ” we “repair” the obstacle surface to make it traversable. Why? • want to avoid modules getting trapped when filling in from east to west • want modules to crawl over obstacle surface as a substrate path during reconfiguration How do we “repair” an obstacle? • form a cone shape with the eastern-most column of the obstacle as its base • fill in this cone from south to north, and from west to east Goal cell Obstacle cell Repaired cell USRG 2002 Unrepaired obstacle Repaired obstacle

Future Work 1. Develop algorithms for dealing with multiple obstacles in the environment. 2. Algorithmic work: • asynchronous reconfiguration algorithms. • procedures for deadlock and collision resolution. • “complete” reconfiguration, from arbitrary initial to arbitrary goal. 3. Build fighting robots. USRG 2002
- Slides: 54