Concurrent Data Structures for NearMemory Computing Zhiyu Liu

Concurrent Data Structures Are used everywhere: kernel, libraries, applications Issues: • Difficult to design

The Memory Wall Data movement 2. 2 GHz = 220 K cycles during this

Near Memory Computing • Also called Processing In Memory (PIM) • Avoid data movement

Near Memory Computing: Architecture PIM memory • Vaults: memory partitions • PIM cores: lightweight

Data Structures + Hardware • Tight integration between algorithmic design and hardware characteristics •

Goals: PIM Concurrent Data Structures 1. How do PIM data structures compare to state-ofthe-art

Pointer Chasing Data Structures 1 4 7 8 10 1 16 10 1 3

Naïve PIM Skiplist CPU add(30) CPU add(5) delete(80) PIM Memory Vault PIM core Low

Concurrent Data Structures CPU CPU add(5) add(30) delete(80) High Latency DRAM 1 4 7

Flat Combining Combiner lock CPU add(30) CPU delete(80) add(5) High Latency Sequential access DRAM

Skiplist Throughput 10000000 Lock-free Intel Xeon E 7 -4850 v 3 28 hardware threads,

PIM Performance N Size of the skiplist p Number of processes LCPU Latency of

PIM Performance LCPU = r 1 LPIM = r 2 LLLC r 1 =

PIM Performance Algorithm Lock-free Throughput p / ( B * LCPU ) Flat Combining

Skiplist Throughput 10000000 Lock-free 9000000 Ops/s 8000000 7000000 6000000 5000000 4000000 PIM (expected) 3000000

New PIM algorithm: Exploit Partitioning PIM memory CPU CPU Crossbar Network PIM core Vault

PIM Skiplist w/ Partitioning CPU CPU 1 10 20 CPU cache PIM Memory PIM

Skiplist Throughput 10000000 Lock-free 9000000 8000000 7000000 Ops/s 6000000 FC w/ 16 partitions 5000000

Skiplist Throughput 18000000 PIM w/ 16 partitions (expected) 16000000 14000000 PIM w/ 8 partitions

PIM FIFO Queue 3 sends back the node CPU Deq() PIM Memory Vault 1

Pipelining Can overlap the execution of the next request Deq() 1 2 3 1

Parallelize Enqs and Deqs CPU CPU enqs PIM core Vault 2 Head deqs PIM

Conclusion PIM is becoming feasible in the near future We investigate Concurrent Data Structures

Thank you! icalciu@vmware. com https: //research. vmware. com/

Slides: 33

Download presentation

Concurrent Data Structures Are used everywhere: kernel, libraries, applications Issues: • Difficult to design and implement • Data layout and memory/cache hierarchy play crucial role in performance Cache Memory 2

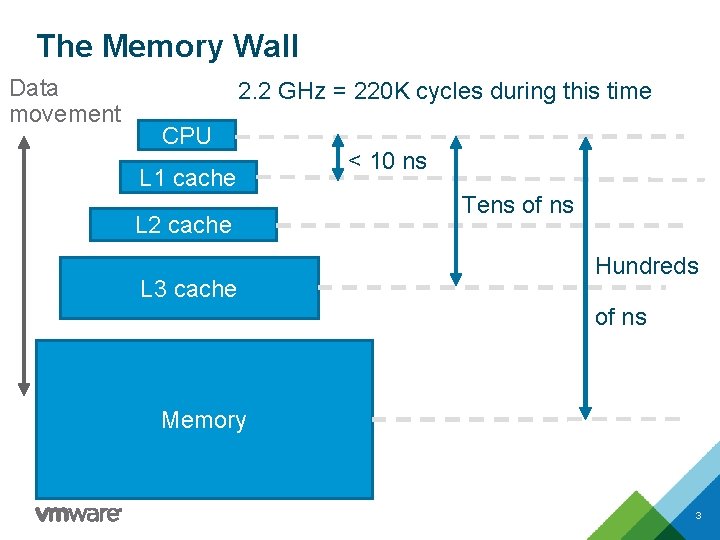
The Memory Wall Data movement 2. 2 GHz = 220 K cycles during this time CPU L 1 cache L 2 cache L 3 cache < 10 ns Tens of ns Hundreds of ns Memory 3

Near Memory Computing • Also called Processing In Memory (PIM) • Avoid data movement by doing computation in memory • Old idea • New advances in 3 D integration and die-stacked memory • Viable in the near future 4

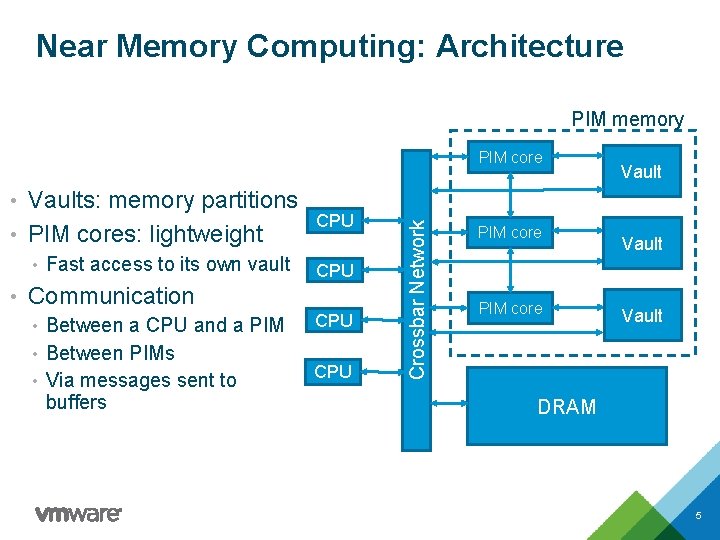
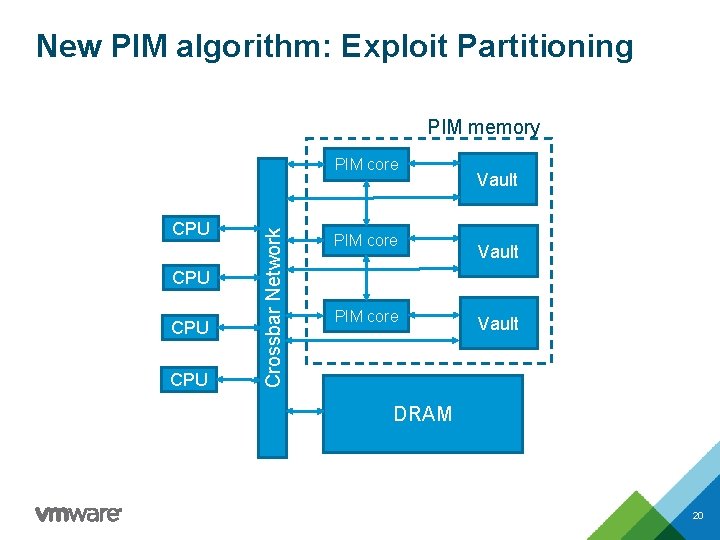
Near Memory Computing: Architecture PIM memory • Vaults: memory partitions • PIM cores: lightweight • Fast access to its own vault CPU • Communication • Between a CPU and a PIM • Between PIMs • Via messages sent to buffers CPU Crossbar Network PIM core Vault DRAM 5

Data Structures + Hardware • Tight integration between algorithmic design and hardware characteristics • Memory becomes an active component in managing data • Managing data structures in PIM • Old work: pointer chasing for sequential data structures • Our work: concurrent data structures 6

Goals: PIM Concurrent Data Structures 1. How do PIM data structures compare to state-ofthe-art concurrent data structures? 2. How to design efficient PIM data structures? LOW Pointer-chasing CONTENTION HIGH Cacheable 7

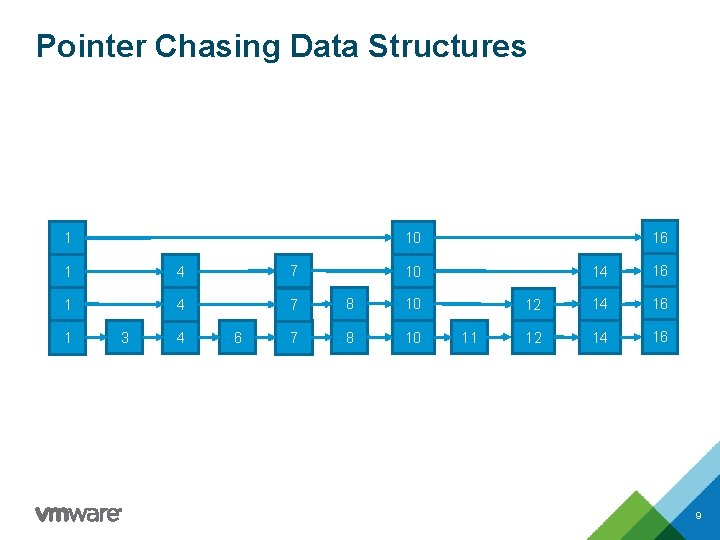
Pointer Chasing Data Structures 1 4 7 8 10 1 16 10 1 3 4 6 14 16 12 14 16 10 11 9

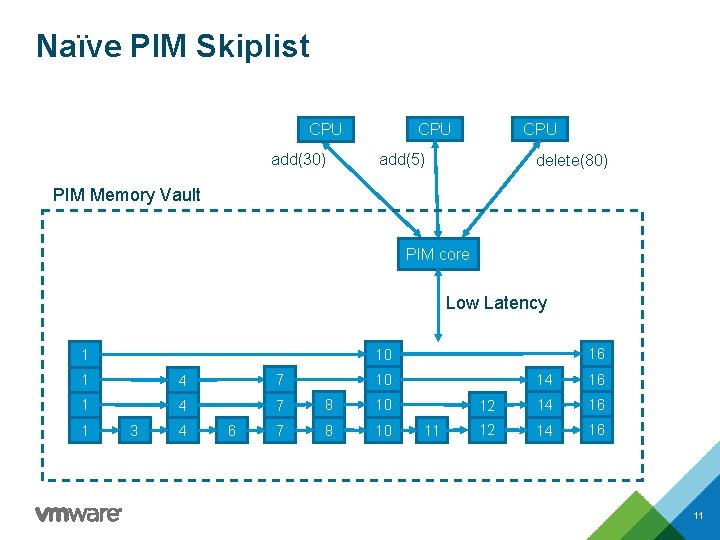
Naïve PIM Skiplist CPU add(30) CPU add(5) delete(80) PIM Memory Vault PIM core Low Latency 1 4 7 8 10 1 16 10 1 3 4 6 14 16 12 14 16 10 11 11

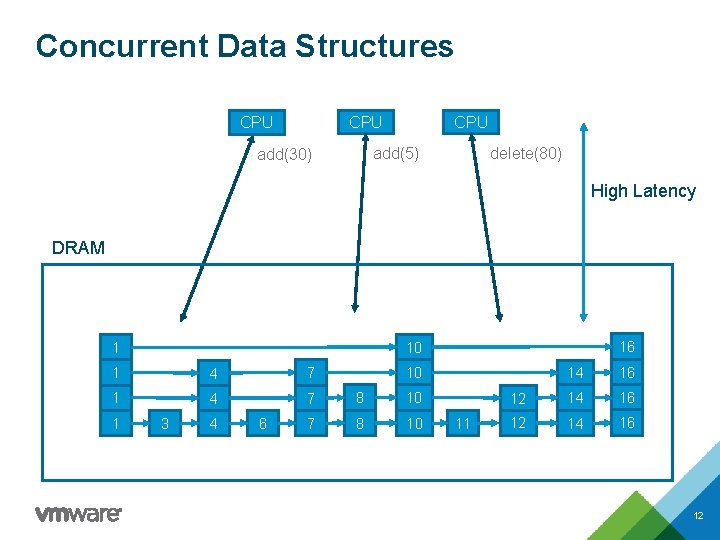
Concurrent Data Structures CPU CPU add(5) add(30) delete(80) High Latency DRAM 1 4 7 8 10 1 16 10 1 3 4 6 14 16 12 14 16 10 11 12

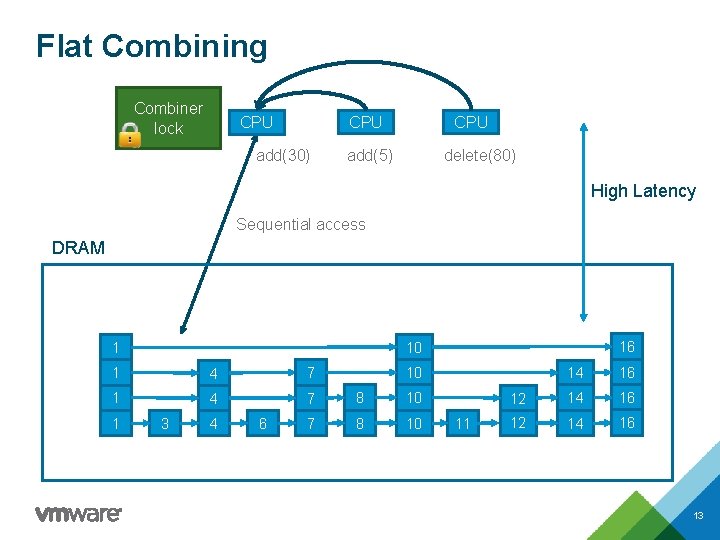
Flat Combining Combiner lock CPU add(30) CPU delete(80) add(5) High Latency Sequential access DRAM 1 4 7 8 10 1 16 10 1 3 4 6 14 16 12 14 16 10 11 13

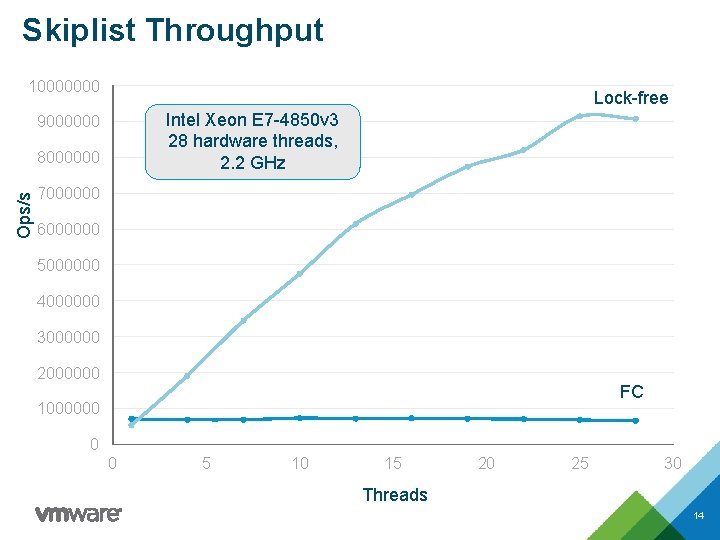
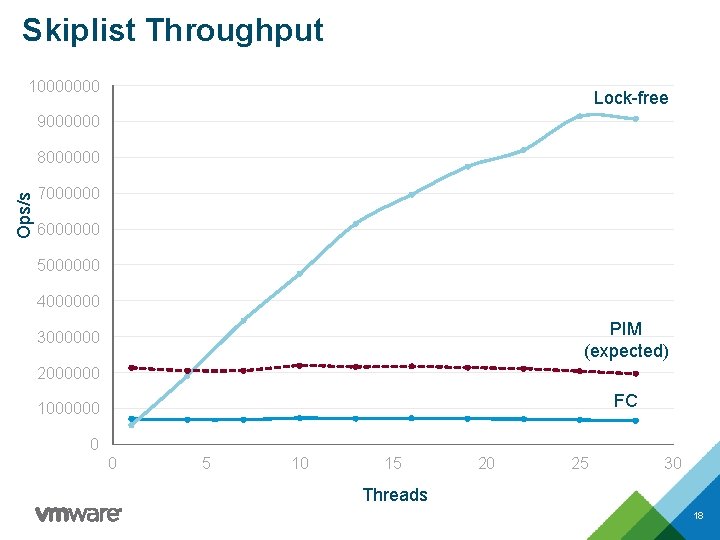
Skiplist Throughput 10000000 Lock-free Intel Xeon E 7 -4850 v 3 28 hardware threads, 2. 2 GHz 9000000 Ops/s 8000000 7000000 6000000 5000000 4000000 3000000 2000000 FC 1000000 0 0 5 10 15 20 25 30 Threads 14

PIM Performance N Size of the skiplist p Number of processes LCPU Latency of a memory access from the CPU LLLC Latency of a LLC access LATOMIC Latency of an atomic instruction (by the CPU) LPIM Latency of a memory access from the PIM core LMSG Latency of a message from the CPU to the PIM core 15

PIM Performance LCPU = r 1 LPIM = r 2 LLLC r 1 = r 2 = 3 LMSG = LCPU 16

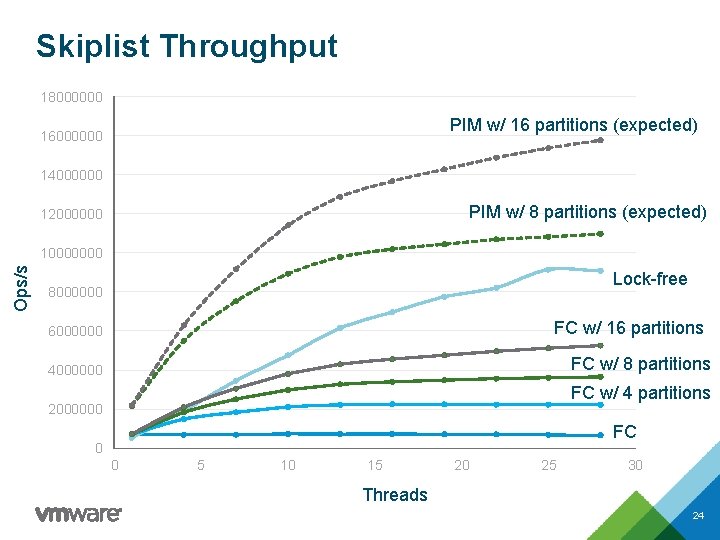
PIM Performance Algorithm Lock-free Throughput p / ( B * LCPU ) Flat Combining (FC) 1 / ( B * LCPU ) PIM 1 / ( B * LPIM + LMSG ) B = average number of nodes accessed during a skiplist operation 17

Skiplist Throughput 10000000 Lock-free 9000000 Ops/s 8000000 7000000 6000000 5000000 4000000 PIM (expected) 3000000 2000000 FC 1000000 0 0 5 10 15 20 25 30 Threads 18

New PIM algorithm: Exploit Partitioning PIM memory CPU CPU Crossbar Network PIM core Vault DRAM 20

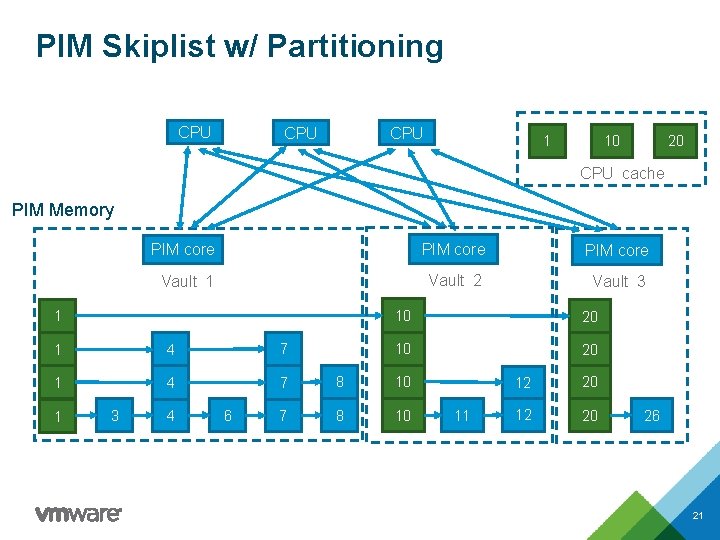
PIM Skiplist w/ Partitioning CPU CPU 1 10 20 CPU cache PIM Memory PIM core Vault 1 Vault 2 Vault 3 1 10 20 1 4 7 8 10 1 3 4 6 11 12 20 26 21

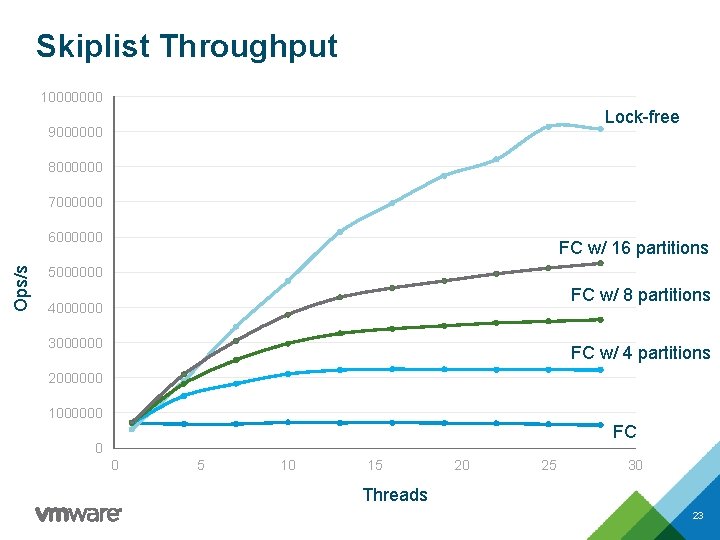
PIM Performance Algorithm Lock-free Throughput p / ( B * LCPU ) Flat Combining (FC) 1 / ( B * LCPU ) PIM 1 / ( B * LPIM + LMSG ) FC + k partitions k / ( B * LCPU ) PIM + k partitions k / ( B * LPIM + LMSG ) B = average number of nodes accessed during a skiplist operation 22

Skiplist Throughput 10000000 Lock-free 9000000 8000000 7000000 Ops/s 6000000 FC w/ 16 partitions 5000000 FC w/ 8 partitions 4000000 3000000 FC w/ 4 partitions 2000000 1000000 FC 0 0 5 10 15 20 25 30 Threads 23

Skiplist Throughput 18000000 PIM w/ 16 partitions (expected) 16000000 14000000 PIM w/ 8 partitions (expected) 12000000 Ops/s 10000000 Lock-free 8000000 FC w/ 16 partitions 6000000 FC w/ 8 partitions 4000000 FC w/ 4 partitions 2000000 FC 0 0 5 10 15 20 25 30 Threads 24

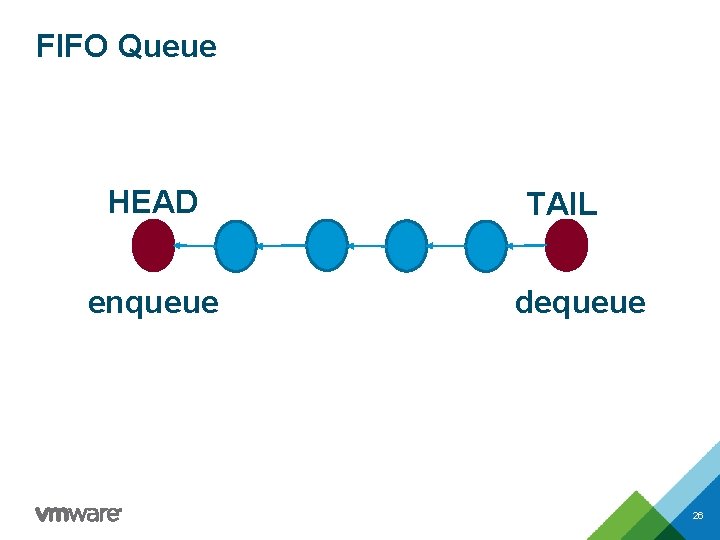
FIFO Queue HEAD enqueue TAIL dequeue 26

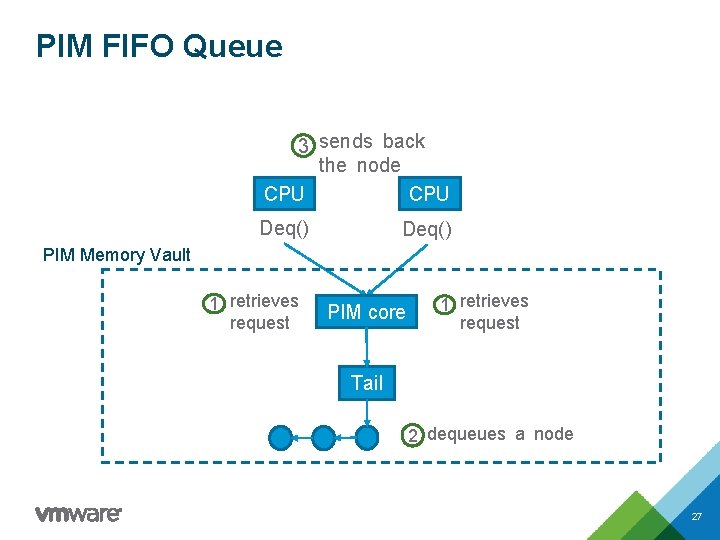
PIM FIFO Queue 3 sends back the node CPU Deq() PIM Memory Vault 1 retrieves request PIM core 1 retrieves request Tail 2 dequeues a node 27

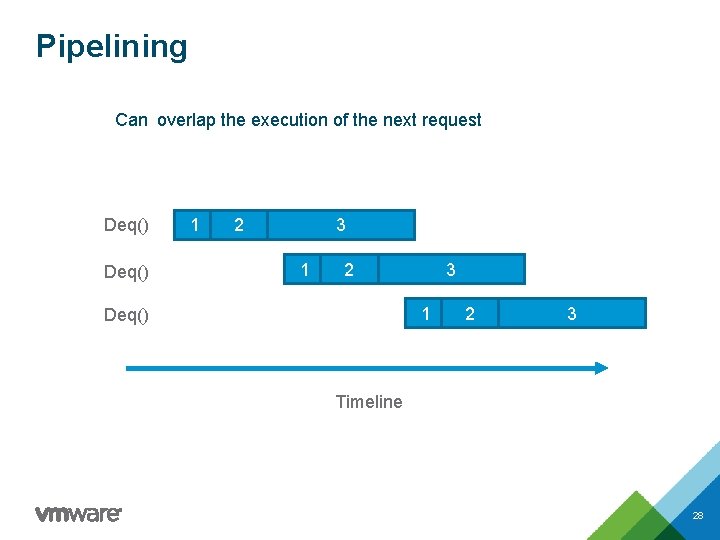
Pipelining Can overlap the execution of the next request Deq() 1 2 3 1 Deq() 2 3 Timeline 28

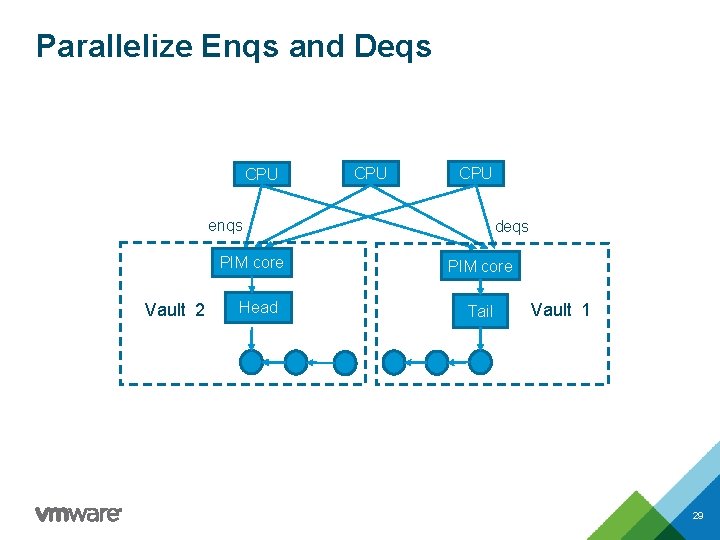
Parallelize Enqs and Deqs CPU CPU enqs PIM core Vault 2 Head deqs PIM core Tail Vault 1 29

Conclusion PIM is becoming feasible in the near future We investigate Concurrent Data Structures (CDS) for PIM Results: • Naïve PIM data structures are less efficient than CDS • New PIM algorithms can leverage PIM features • They outperform efficient CDS • They are simpler to design and implement 30

Thank you! icalciu@vmware. com https: //research. vmware. com/