Concurrency Control Techniques Prepared by Remedios de Dios

Concurrency Control Techniques Prepared by: Remedios de Dios Bulos

Outline • Lock-Based Protocols – What is locking? – What are locks? – Binary locks – Shared/ Exclusive locks (Read/Write Locks) • Timestamp-Based Protocols • Validation-Based Protocols

What is locking? • It is a procedure used to control concurrent access to data; • When one data is accessing the database, a lock may deny access to other transactions to prevent incorrect results; • Ensures serializability of concurrent transactions;

Concurrency Problems Lost update problem Time T 1 T 2 balx t 1 begin _transaction 100 t 2 begin _transaction read(balx) 100 t 3 read(balx) balx=balx + 100 t 4 balx=balx - 10 write(balx) 200 t 5 write(balx) t 6 commit 90 90 Solution: Prevent T 1 from reading the value of balx until after T 2‘s update has been completed. balx should be 190.

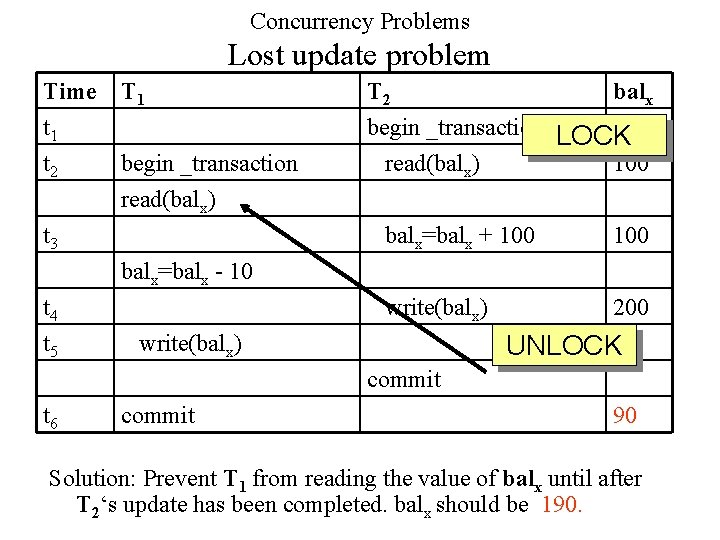
Concurrency Problems Lost update problem Time t 1 t 2 T 1 begin _transaction read(balx) t 3 T 2 balx begin _transaction LOCK 100 read(balx) 100 balx=balx + 100 balx=balx - 10 t 4 t 5 write(balx) 200 UNLOCK 90 commit t 6 commit 90 Solution: Prevent T 1 from reading the value of balx until after T 2‘s update has been completed. balx should be 190.

What is a lock? • A variable associated with a data item that describes the status of the item with respect to possible operations that can be applied to it. • Generally, there is one lock for each data item in the database. X lock-X Y lock-Y Z lock-Z

Types of Locks • Binary locks: • only two states of a lock; • too simple and too restrictive; • not used in practice. • Shared/exclusive locks: which provide more general locking capabilities and are used in practical database locking schemes. • Read Lock as a shared lock, • Write Lock as an exclusive lock.

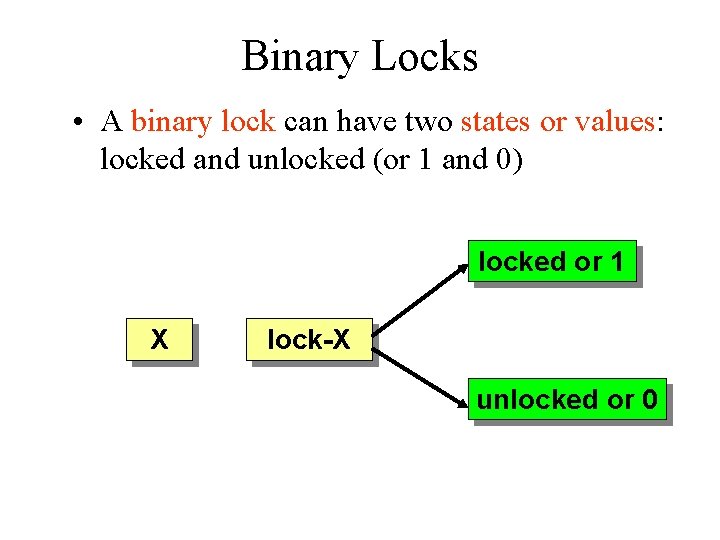
Binary Locks • A binary lock can have two states or values: locked and unlocked (or 1 and 0) locked or 1 X lock-X unlocked or 0

Binary Locks • A binary lock enforces mutual exclusion on the data item; i. e. , at a time, only one transaction can hold a lock. HOLDS lock on X T 1 Can’t HOLD a lock on X T 2

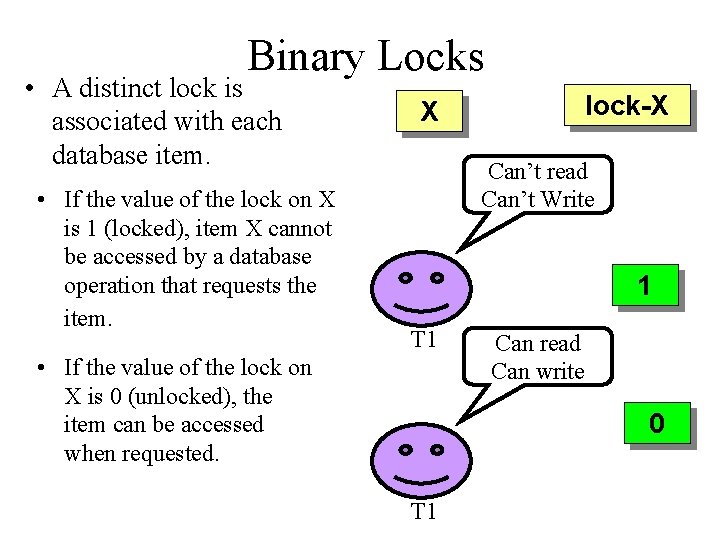
Binary Locks • A distinct lock is associated with each database item. • If the value of the lock on X is 1 (locked), item X cannot be accessed by a database operation that requests the item. lock-X X Can’t read Can’t Write 1 T 1 • If the value of the lock on X is 0 (unlocked), the item can be accessed when requested. Can read Can write 0 T 1

Operations on Binary Locks • lock(X) • unlock(X)

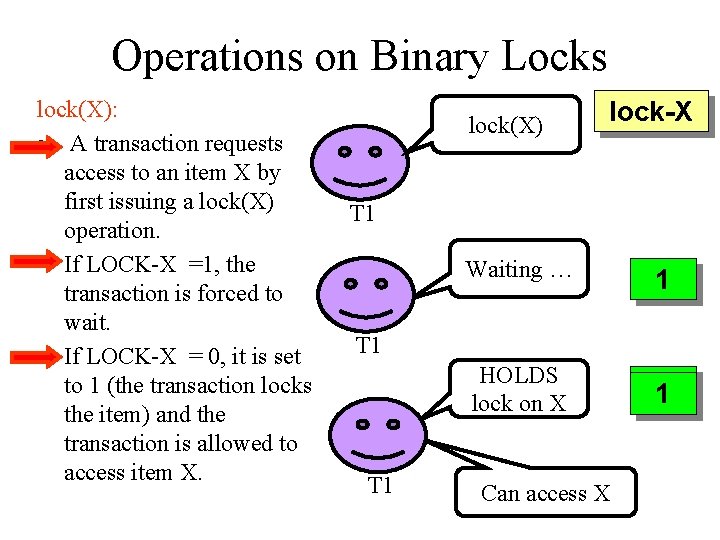
Operations on Binary Locks lock(X): • A transaction requests access to an item X by first issuing a lock(X) operation. • If LOCK-X =1, the transaction is forced to wait. • If LOCK-X = 0, it is set to 1 (the transaction locks the item) and the transaction is allowed to access item X. lock(X) lock-X T 1 Waiting … 1 HOLDS lock on X 0 1 T 1 Can access X

Algorithm: lock(X) B: if LOCK-X =0 (*item is unlocked) then LOCK-X 1 (*lock the item) else begin wait (until lock-X =0 and the lock manager wakes up the transaction) go to B end;

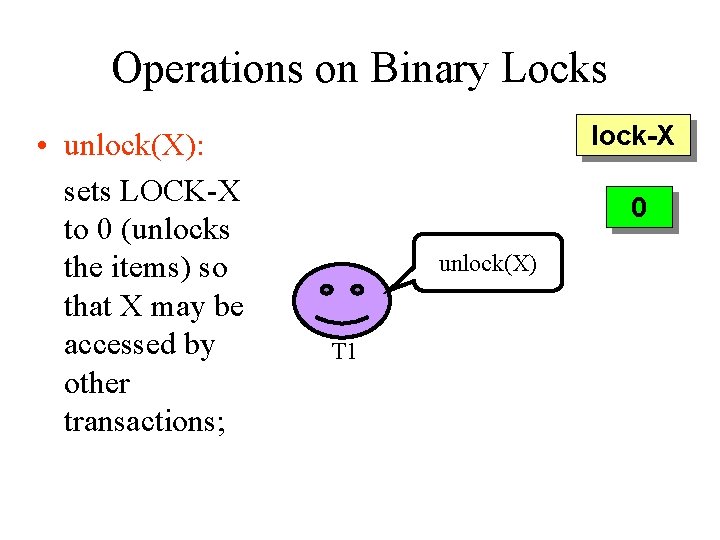
Operations on Binary Locks • unlock(X): sets LOCK-X to 0 (unlocks the items) so that X may be accessed by other transactions; lock-X 0 1 unlock(X) T 1

Algorithm: unlock(X) LOCK-X 0 (*unlock the item) if any transactions are waiting then wakeup one of the waiting transactions

Operations on Binary Locks • lock(X) and unlock(X) operations must be implemented as indivisible units; that is, no interleaving should be allowed once a lock or unlock operation is started until the operation terminates or the transaction must wait until the lock_item goes through.

Operations on Binary Locks • wait command within the lock(X) operation is usually implemented by putting the transaction on a waiting queue for item X until X is unlocked and the transaction can be granted access to it. Other transactions that also want to access X are placed on the same queue. Hence, the wait is considered to be outside the lock(X) operation.

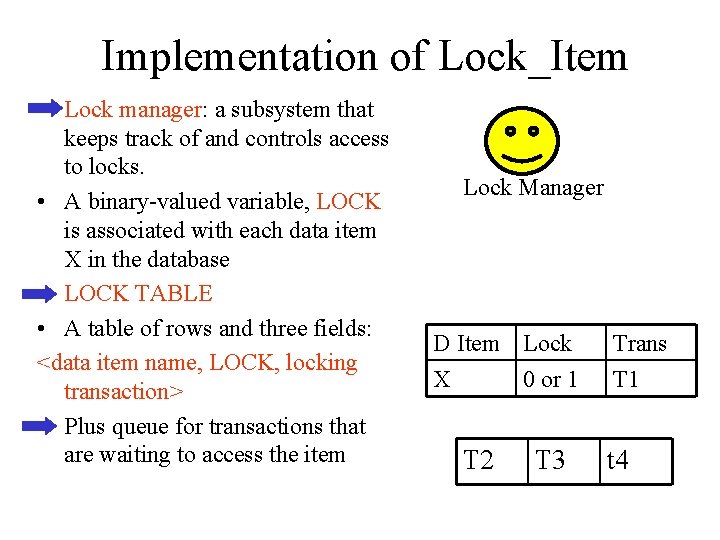
Implementation of Lock_Item • Lock manager: a subsystem that keeps track of and controls access to locks. • A binary-valued variable, LOCK is associated with each data item X in the database • LOCK TABLE • A table of rows and three fields: <data item name, LOCK, locking transaction> • Plus queue for transactions that are waiting to access the item Lock Manager D Item Lock X 0 or 1 T 2 T 3 Trans T 1 t 4

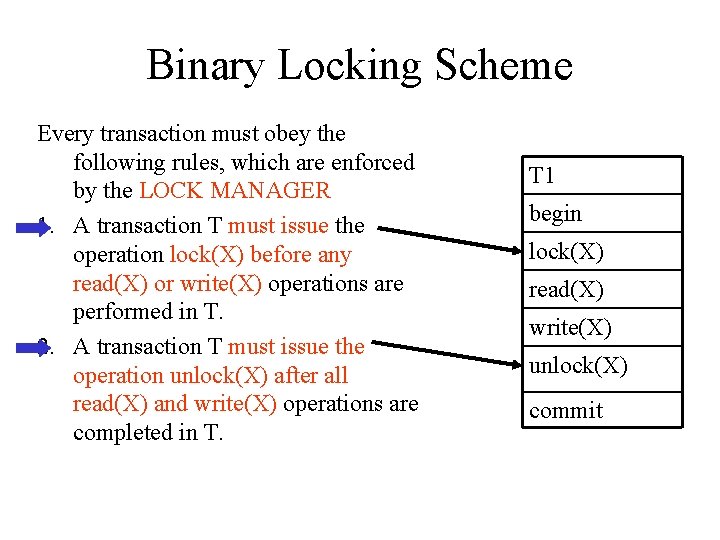
Binary Locking Scheme Every transaction must obey the following rules, which are enforced by the LOCK MANAGER 1. A transaction T must issue the operation lock(X) before any read(X) or write(X) operations are performed in T. 2. A transaction T must issue the operation unlock(X) after all read(X) and write(X) operations are completed in T. T 1 begin lock(X) read(X) write(X) unlock(X) commit

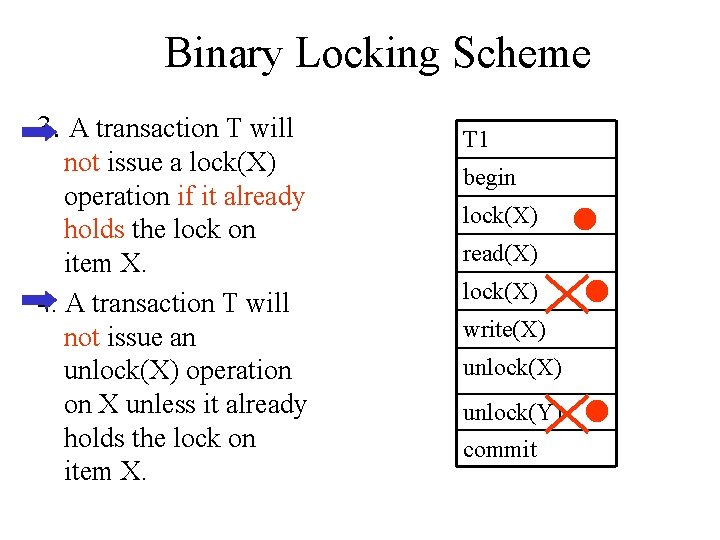
Binary Locking Scheme 3. A transaction T will not issue a lock(X) operation if it already holds the lock on item X. 4. A transaction T will not issue an unlock(X) operation on X unless it already holds the lock on item X. T 1 begin lock(X) read(X) lock(X) write(X) unlock(Y) commit

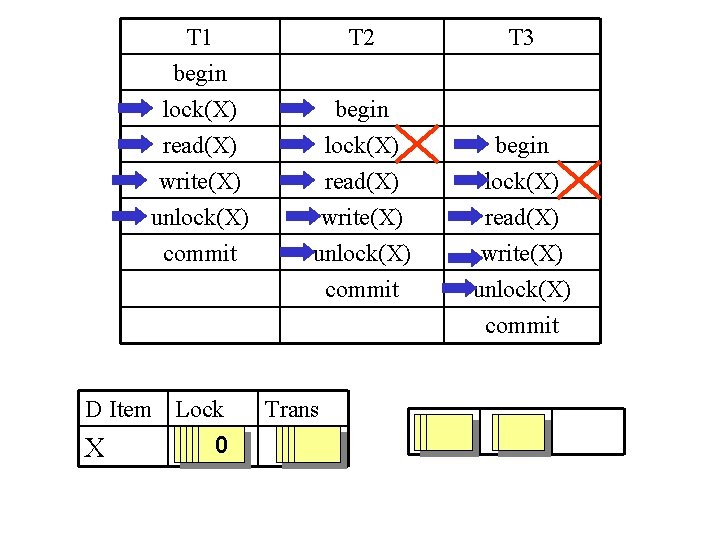
T 1 begin lock(X) read(X) T 2 T 3 begin lock(X) begin write(X) unlock(X) read(X) write(X) lock(X) read(X) commit unlock(X) commit write(X) unlock(X) commit D Item Lock Trans 0 101100 T 1 T 2 T 3 X T 2 T 3

Problem: Given two schedules T 1 and T 2. T 1 transfers an amount (500) from account X to account Y. T 2 deposits an amount (1000) to account X. Initial values of X = 8, 500; Y = 3, 500. Solution: After the successful execution of both transactions, the final values should be: Schedule T 1, T 2: X = 9000; Y = 4000 Schedule T 2, T 1: X = 9000; Y = 4000

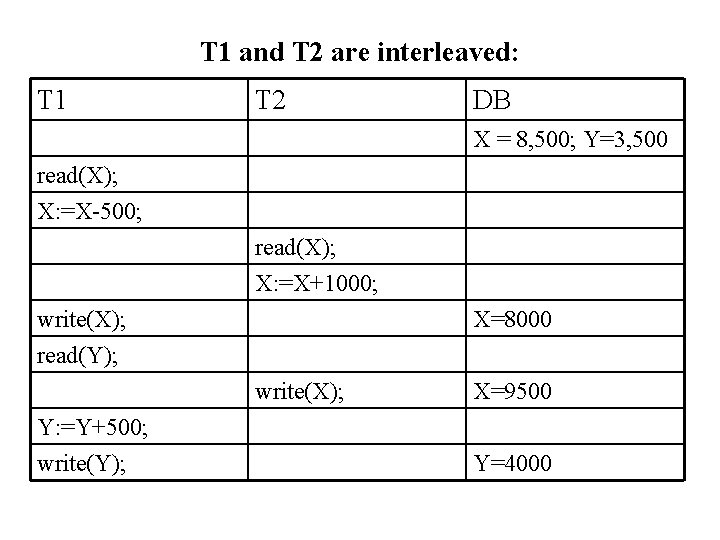
T 1 and T 2 are interleaved: T 1 T 2 DB X = 8, 500; Y=3, 500 read(X); X: =X-500; read(X); X: =X+1000; write(X); read(Y); X=8000 write(X); Y: =Y+500; write(Y); X=9500 Y=4000

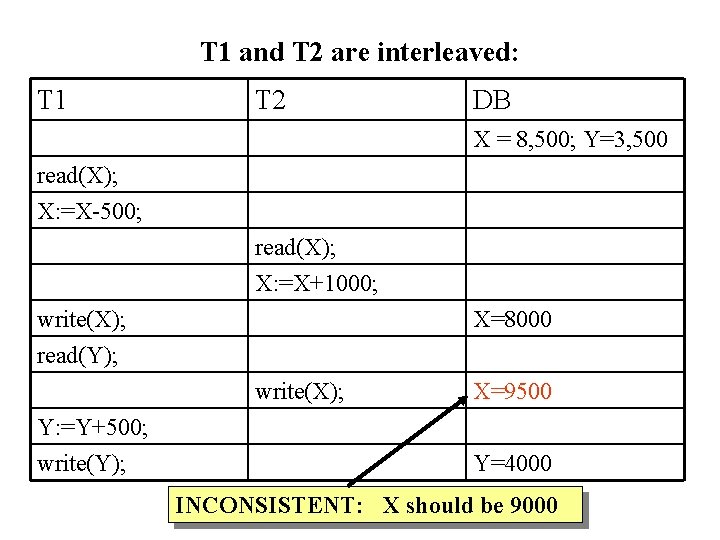
T 1 and T 2 are interleaved: T 1 T 2 DB X = 8, 500; Y=3, 500 read(X); X: =X-500; read(X); X: =X+1000; write(X); read(Y); X=8000 write(X); Y: =Y+500; write(Y); X=9500 Y=4000 INCONSISTENT: X should be 9000

What went wrong? T 2 reads the value of X (old) before T 1‘s update of X has been completed. T 1 T 2 DB X = 8, 500; Y=3, 500 read(X); X: =X-500; read(X); X: =X+1000; write(X); read(Y); X=8000 write(X); Y: =Y+500; write(Y); X=9500 Y=4000

Solution: Prevent T 2 from reading the value of X until after T 1‘s update of X has been completed. T 1 T 2 DB X = 8, 500; Y=3, 500 read(X); X: =X-500; read(X); X: =X+1000; write(X); read_item(Y); X=8000 write(X); Y: =Y+500; write(Y); X=9500 Y=4000

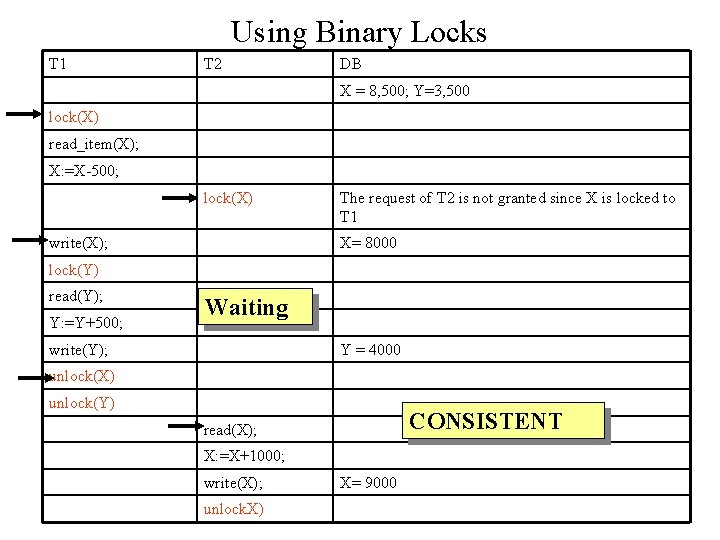
Using Binary Locks T 1 T 2 DB X = 8, 500; Y=3, 500 lock(X) read_item(X); X: =X-500; lock(X) write(X); The request of T 2 is not granted since X is locked to T 1 X= 8000 lock(Y) read(Y); Y: =Y+500; Waiting write(Y); Y = 4000 unlock(X) unlock(Y) CONSISTENT read(X); X: =X+1000; write(X); unlock. X) X= 9000

Binary Locking Problems • Problem: – T 1: adds the value of item A to items B to Z; – T 2: queries the value of item A

T 1 T 2 DB lock(A) The request of T 2 is not granted since A is locked to T 1 lock(A) read(A); lock(B) read(B); B: =B+A; … lock(Z) Waiting read(B); Z: =Z+A; unlock(A) read(A); print(A); unlock(A) unlock(B) … Problem: Too restrictive, that is, at most only one transaction can hold a lock on a given item Solution: Allow several transactions to access the same item, if the access is for reading purposes only T 2 is finally allowed to access item A.

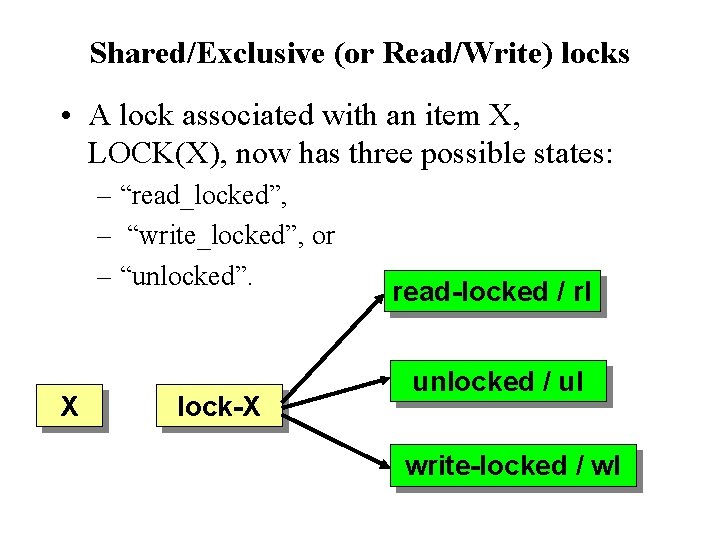
Shared/Exclusive (or Read/Write) locks • A lock associated with an item X, LOCK(X), now has three possible states: – “read_locked”, – “write_locked”, or – “unlocked”. X lock-X read-locked / rl unlocked / ul write-locked / wl

Shared/Exclusive (or Read/Write) locks A read_locked item is also called shared-locked, because other transactions are allowed to read the item. A write_locked item is called exclusive-locked, because a single transaction exclusively holds the lock on the item

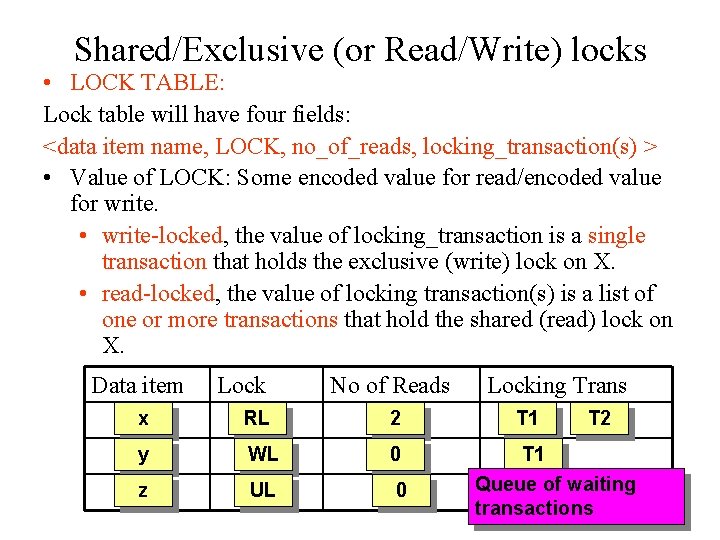
Shared/Exclusive (or Read/Write) locks • LOCK TABLE: Lock table will have four fields: <data item name, LOCK, no_of_reads, locking_transaction(s) > • Value of LOCK: Some encoded value for read/encoded value for write. • write-locked, the value of locking_transaction is a single transaction that holds the exclusive (write) lock on X. • read-locked, the value of locking transaction(s) is a list of one or more transactions that hold the shared (read) lock on X. Data item Lock No of Reads x RL 2 y WL 0 z UL 0 Locking Trans T 1 T 2 T 1 Queue of waiting transactions

Shared/Exclusive (or Read/Write) locks Rules for Read/Write Locks 1. A transaction T must issue the operation read_lock(X) or write_lock(X) before any read(X) operation is performed in T. 2. 2. A transaction T must issue the operation write_lock(X) before any write(X) operation is performed in T. T 1 T 2 begin read-lock(X) write-lock(X) read(X) write-lock(X) write(X) unlock(X) commit

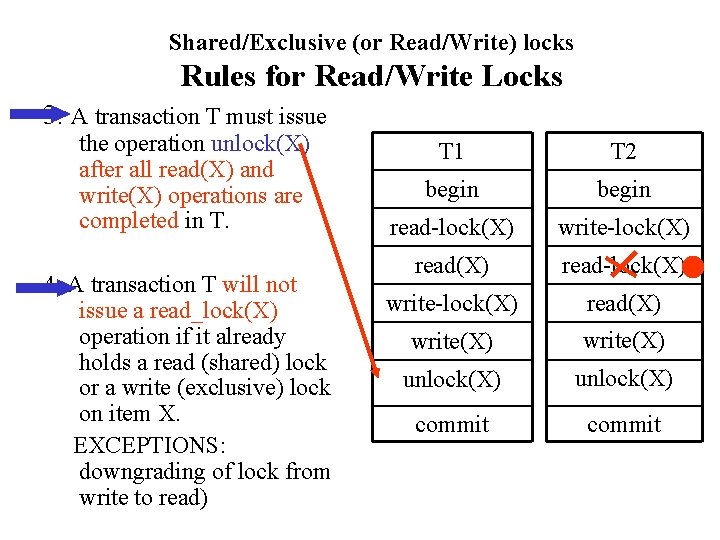
Shared/Exclusive (or Read/Write) locks Rules for Read/Write Locks 3. A transaction T must issue the operation unlock(X) after all read(X) and write(X) operations are completed in T. 4. A transaction T will not issue a read_lock(X) operation if it already holds a read (shared) lock or a write (exclusive) lock on item X. EXCEPTIONS: downgrading of lock from write to read) T 1 T 2 begin read-lock(X) write-lock(X) read(X) write(X) unlock(X) commit

Shared/Exclusive (or Read/Write) locks Rules for Read/Write Locks 5. A transaction T will not issue T 1 T 2 begin write-lock(X) read(X) Exceptions: Upgrading of lock from read to write) write-lock(X) write(X) 6. A transaction T will not issue an unlock(X) operation unless it already holds a read (shared) lock or a write (exclusive) lock on item X. unlock(X) commit unlock(Y) a write_lock(X) operation if it already holds a read(shared) lock or write (exclusive) lock on item X. commit

Algorithm: read_lock(X) B: if LOCK(X) = “unlocked” then begin LOCK(X) “read-locked”; no_of_reads(X) 1 end elseif LOCK(X) = “read-locked” then no_of_read(X) no_of_reads(X) + 1 else begin wait (until LOCK(X) = “unlocked” and the lock manager wakes up the transaction); go to B end

Algorithm: write_lock(X) B: if LOCK(X) = “unlocked” then begin LOCK(X) “write-locked”; else wait (until LOCK(X) = “unlocked” and the lock manager wakes up the transaction); go to B end;

Algorithm: unlock(X) B: if LOCK(X) = “write-locked” then begin LOCK(X) “unlocked”; wakeup one of the waiting transactions, if any end else if LOCK(X) = “read-locked” then begin no_of_read(X) no_of_reads(X) - 1 if no_of_reads(X)=0 then begin LOCK(X) =“unlocked” wakeup one of the waiting transactions, if any end;

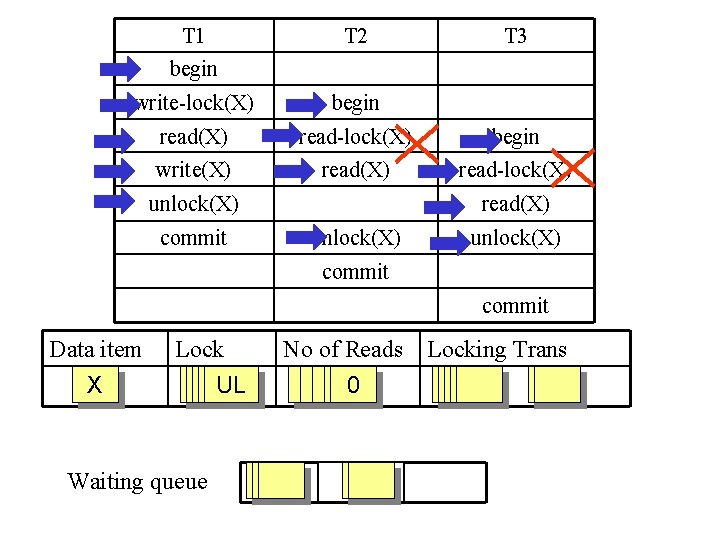
T 1 T 2 T 3 begin write-lock(X) begin read(X) read-lock(X) begin write(X) read-lock(X) unlock(X) read(X) commit unlock(X) commit Data item X Lock No of Reads UL WL UL RL UL Waiting queue 01210 T 2 T 3 Locking Trans T 1 T 2 T 3

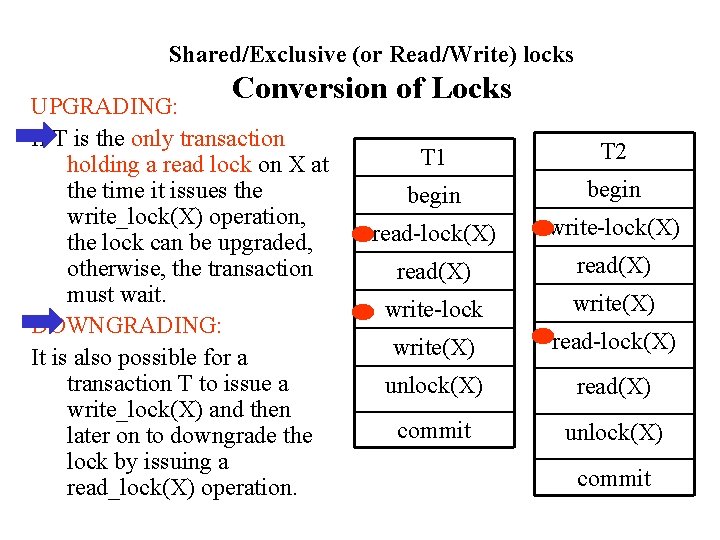
Shared/Exclusive (or Read/Write) locks Conversion of Locks UPGRADING: If T is the only transaction holding a read lock on X at the time it issues the write_lock(X) operation, the lock can be upgraded, otherwise, the transaction must wait. DOWNGRADING: It is also possible for a transaction T to issue a write_lock(X) and then later on to downgrade the lock by issuing a read_lock(X) operation. T 1 T 2 begin read-lock(X) write-lock(X) read(X) write-lock write(X) read-lock(X) unlock(X) read(X) commit unlock(X) commit

Lock-compatibility matrix S X s true false x false

Example • Problem: – T 1: adds the value of item A to items B to Z; – T 2: queries the value of item A

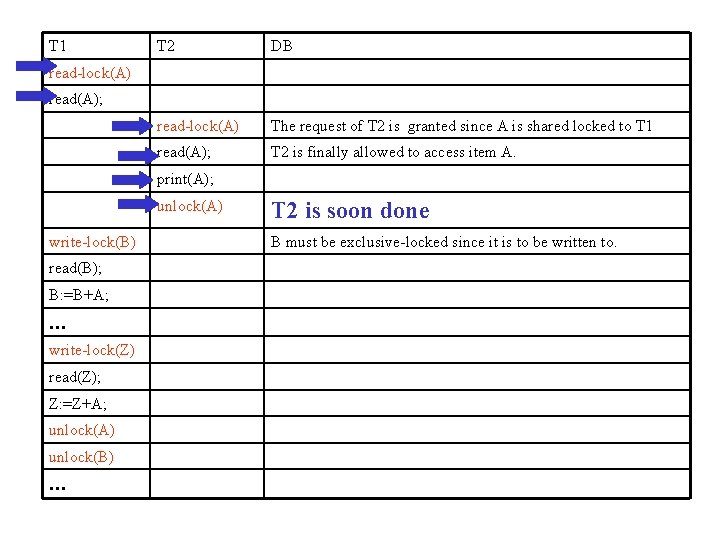
T 1 T 2 DB read-lock(A) The request of T 2 is granted since A is shared locked to T 1 read(A); T 2 is finally allowed to access item A. read-lock(A) read(A); print(A); unlock(A) write-lock(B) read(B); B: =B+A; … write-lock(Z) read(Z); Z: =Z+A; unlock(A) unlock(B) … T 2 is soon done B must be exclusive-locked since it is to be written to.

However, locking can violate serializability

Locking: Violation of Serializability Problem: Given two transaction T 1 and T 2 T 1 adds the content of Y to X; ( X = X+Y) T 2 adds the content of X to Y; (Y = Y + X) Initial values : X= 20, Y=30 Solution 1: T 1, T 2 T 1: X = X + Y; 20+30; X= 50 ; Y=30 T 2: Y = Y + X; 30+50; X=50; Y=80 Solution 2: T 2, T 1 T 2: Y = Y + X; 30+20; X=20; Y=50 T 1: X = X + Y; 20+50; X= 70 ; Y=50

Serial Schedule: T 1, T 2 T 1 T 2 DB X=20; Y=30 read(Y); read(X); X: =X+Y; write(X) X = 50 read(X); New value of X is read, which is 50 read(Y) Y=Y+X write(Y) Y = 80 Old value of Y is read, which is 30

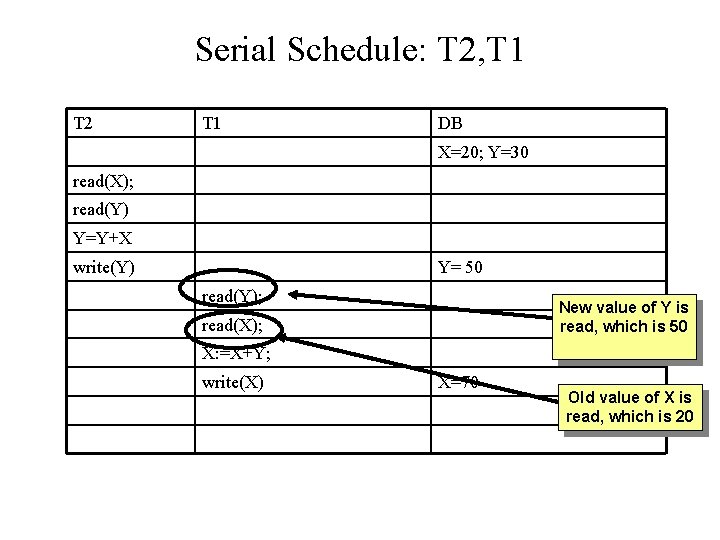
Serial Schedule: T 2, T 1 T 2 T 1 DB X=20; Y=30 read(X); read(Y) Y=Y+X write(Y) Y= 50 read(Y); New value of Y is read, which is 50 read(X); X: =X+Y; write(X) X=70 Old value of X is read, which is 20

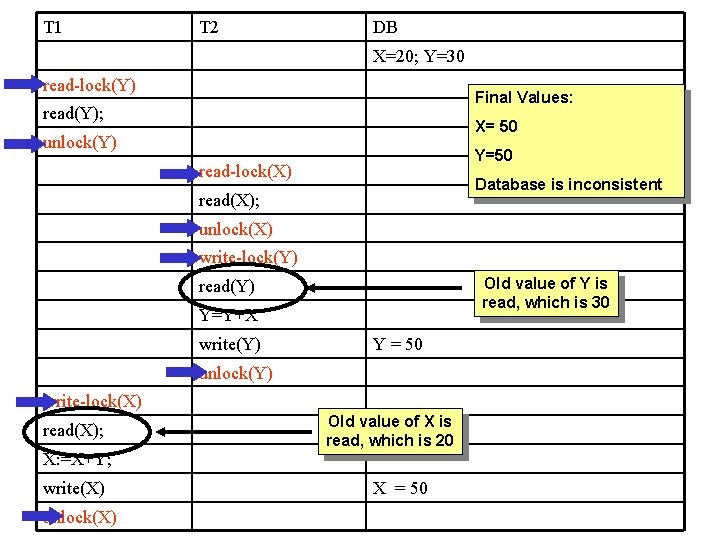
T 1 T 2 DB X=20; Y=30 read-lock(Y) Final Values: read(Y); X= 50 unlock(Y) Y=50 read-lock(X) Database is inconsistent read(X); unlock(X) write-lock(Y) Old value of Y is read, which is 30 read(Y) Y=Y+X write(Y) Y = 50 unlock(Y) write-lock(X) read(X); X: =X+Y; write(X) unlock(X) Old value of X is read, which is 20 X = 50

Locking Can Violate Serializability Findings: • T 1, T 2: X=50; Y=80 • T 2, T 1: X=70, Y=50 • Interleaved schedule using R/W locking: X=50; Y=50 • Therefore, interleaved schedule is not serializable

What is wrong with the example?

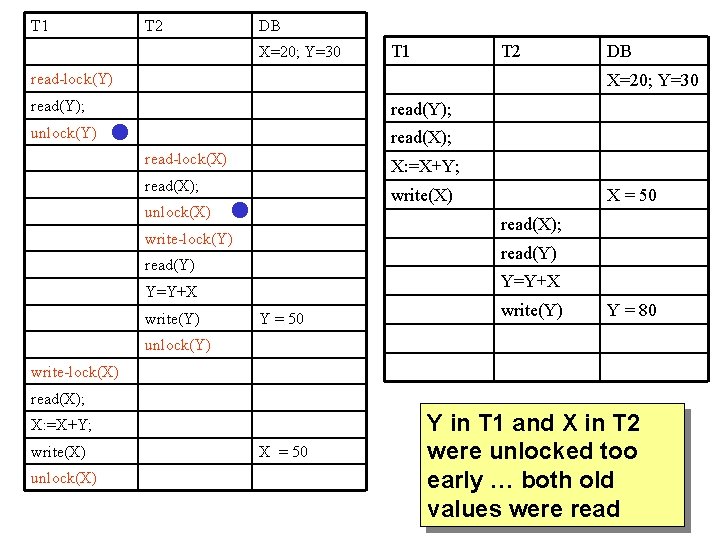
T 1 T 2 DB X=20; Y=30 read-lock(Y) read(Y); unlock(Y) read(X); read-lock(X) X: =X+Y; read(X); write(X) unlock(X) read(X); write-lock(Y) read(Y) Y=Y+X write(Y) X = 50 Y = 50 write(Y) Y = 80 unlock(Y) write-lock(X) read(X); X: =X+Y; write(X) unlock(X) X = 50 Y in T 1 and X in T 2 were unlocked too early … both old values were read

Locking Can Violate Serializability Problem: Given two transaction T 9 and T 10 T 9 : transfers 100 from Y to X T 10 : increases the amounts of X and Y by 10% X= X *1. 1; Y = Y * 1. 1 Initial values : X= 100, Y=400 Solution 1: T 9, T 10 T 9: X = X + 100 = 200; Y= Y – 100 = 300 T 10: X=200 * 1. 1 =220 Y = 300 * 1. 1 = 330 Solution 2: T 10, T 9 T 10: X=100 * 1. 1 =110 Y = 400* 1. 1 = 440 T 9: X = X + 100 = 210; Y= Y – 100 = 340

T 9 write_lock(T 9, X) T 10 begin _transaction read(X) X=X + 100 unlock(T 9, X) write(X) X=X * 1. 1 write(X) unlock(T 10, X) unlock(T 9, Y) X=220 read(baly) write_lock(T 10, Y) write_lock(T 9, Y) X=200 read(X) write_lock(T 10, X) unlock(T 10, Y) begin _transaction Y=Y * 1. 1 write(Y) read(Y) Y=440 commit Y=Y - 100 write(Y) commit Y=340

Locking Can Violate Serializability Findings: • T 9, T 10: X=220; Y=330 • T 10, T 9: X=210, Y=340 • Interleaved schedule using R/W locking: X=220; Y=340 • Therefore, interleaved schedule is not serializable

What is wrong with the example?

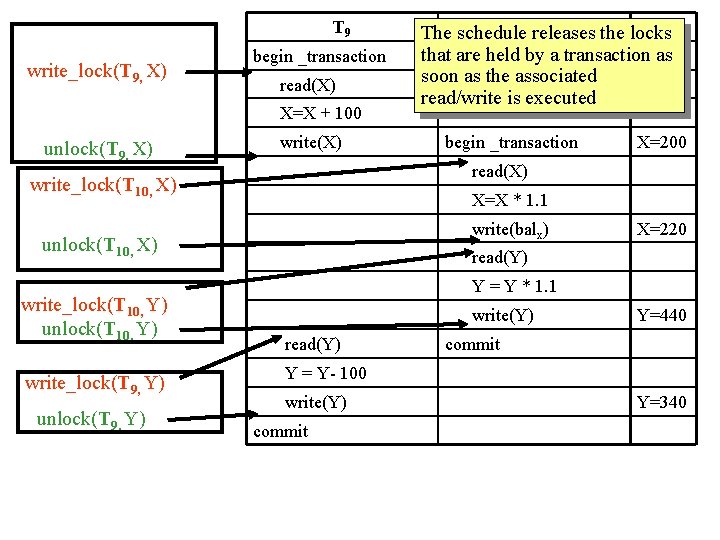
T 9 write_lock(T 9, X) begin _transaction read(X) X=X + 100 unlock(T 9, X) write(X) unlock(T 9, Y) X=200 X=X * 1. 1 write(balx) unlock(T 10, X) write_lock(T 9, Y) begin _transaction read(X) write_lock(T 10, Y) unlock(T 10, Y) 10 The schedule. Treleases the locks that are held by a transaction as soon as the associated read/write is executed X=220 read(Y) Y = Y * 1. 1 write(Y) read(Y) Y=440 commit Y = Y- 100 write(Y) commit Y=340

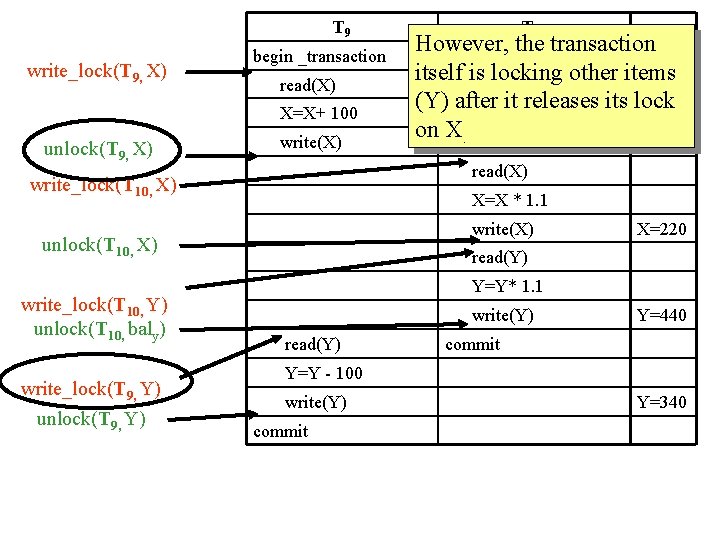
T 9 write_lock(T 9, X) begin _transaction read(X) X=X+ 100 unlock(T 9, X) write(X) X=X * 1. 1 write(X) unlock(T 10, X) write_lock(T 9, Y) unlock(T 9, Y) However, the transaction itself is locking other items (Y) after it releases its lock on begin X. _transaction X=200 read(X) write_lock(T 10, Y) unlock(T 10, baly) T 10 X=220 read(Y) Y=Y* 1. 1 write(Y) read(Y) Y=440 commit Y=Y - 100 write(Y) commit Y=340

Two-phase locking (2 PL): definition • A transaction follows the two-phase locking protocol, if all locking operations (read_lock, write_lock) precede the first unlock operation in the transaction. T 1 begin read-lock(Y) read(Y); write-lock(X) read(X); X: =X+Y; write(X) unlock(Y) unlock(X) commit

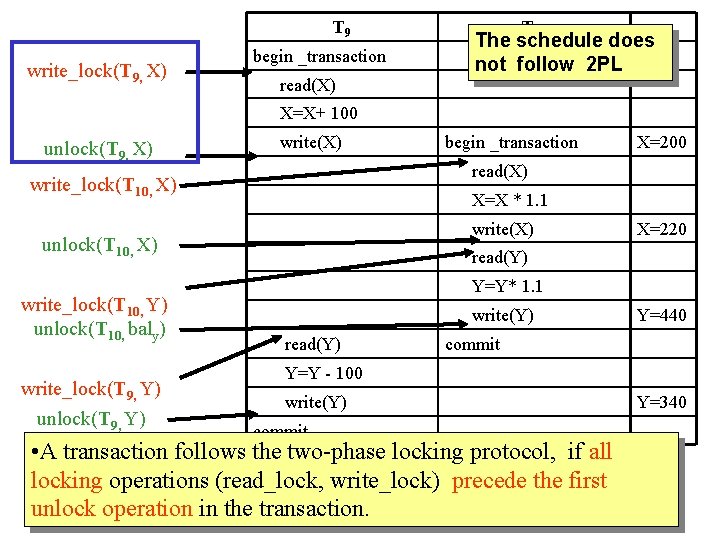
T 9 write_lock(T 9, X) begin _transaction read(X) T 10 The schedule does not follow 2 PL X=X+ 100 unlock(T 9, X) write(X) X=X * 1. 1 write(X) unlock(T 10, X) write_lock(T 9, Y) unlock(T 9, Y) X=200 read(X) write_lock(T 10, Y) unlock(T 10, baly) begin _transaction X=220 read(Y) Y=Y* 1. 1 write(Y) read(Y) Y=440 commit Y=Y - 100 write(Y) commit • A transaction follows the two-phase locking protocol, if all locking operations (read_lock, write_lock) precede the first unlock operation in the transaction. Y=340

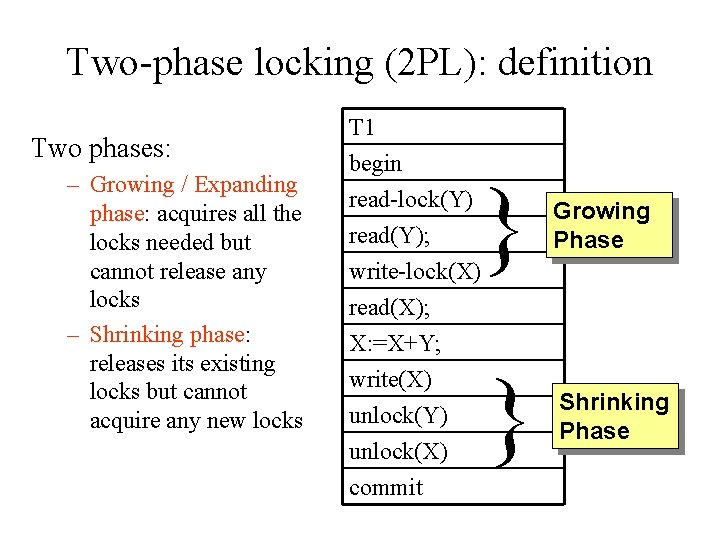
Two-phase locking (2 PL): definition Two phases: – Growing / Expanding phase: acquires all the locks needed but cannot release any locks – Shrinking phase: releases its existing locks but cannot acquire any new locks T 1 begin read-lock(Y) read(Y); write-lock(X) read(X); X: =X+Y; write(X) unlock(Y) unlock(X) commit } Growing Phase } Shrinking Phase

2 PL (Basic): Rules • A transaction must acquire a lock on an item before operating on the item. The lock may be read or write depending on the type of access needed. • Once a transaction releases a lock, it can never acquire any new locks.

Upgrading/Downgrading locks with 2 PL • Upgrading of locks (from read-locked to write-locked) must be done during the expanding phase. • Downgrading of locks (from write-locked to read-locked) must be done in the shrinking phase. Hence, a read_lock(X) operation that downgrades an already held write lock on X can appear only in the shrinking phase.

Claims of 2 PL 1. If every transaction in a schedule follows the two-phase locking protocol, the schedule is guaranteed to be serializable, obviating the need to test for serializability schedules. 2. If the locking mechanism enforces twophase locking rules, it in effect enforces serializability.

2 PL Upholds Serializability It has a cyclic precedence graph; it is not conflict serializable. This schedule becomes (conflict) serializable using 2 PL below: T 1 T 2 write_lock(X); read_item(X); write_lock(X); write_item(X); unlock(X); T 3 It has an acyclic precedence graph; it is not conflict serializable. write_item(X); unlock(X);

2 PL Example • Problem – T 1 transfers 50 from account A to B – T 2 displays the sum of accounts and B – Initial Values: A =100; B=200

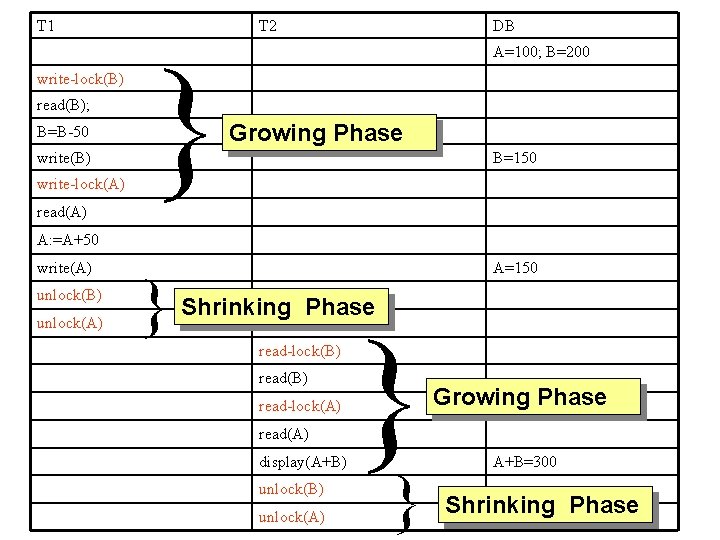
T 1 write-lock(B) read(B); B=B-50 write(B) write-lock(A) read(A) T 2 } DB A=100; B=200 Growing Phase B=150 A: =A+50 write(A) unlock(B) unlock(A) } A=150 Shrinking Phase read-lock(B) read-lock(A) read(A) display(A+B) unlock(A) } } Growing Phase A+B=300 Shrinking Phase

2 -Phase Locking Problem: Given two transaction T 1 and T 2 T 1 adds the content of Y to X; ( X = X+Y) T 2 adds the content of X to Y; (Y = Y + X) Initial values : X= 20, Y=30 Solution 1: T 1, T 2 Solution 2: T 2, T 1: X = X + Y; 20+30; T 2: Y = Y + X; 30+20; X= 50 ; Y=30 X=20; Y=50 T 2: Y = Y + X; 30+50; T 1: X = X + Y; 20+50; X=50; Y=80 X= 70 ; Y=50

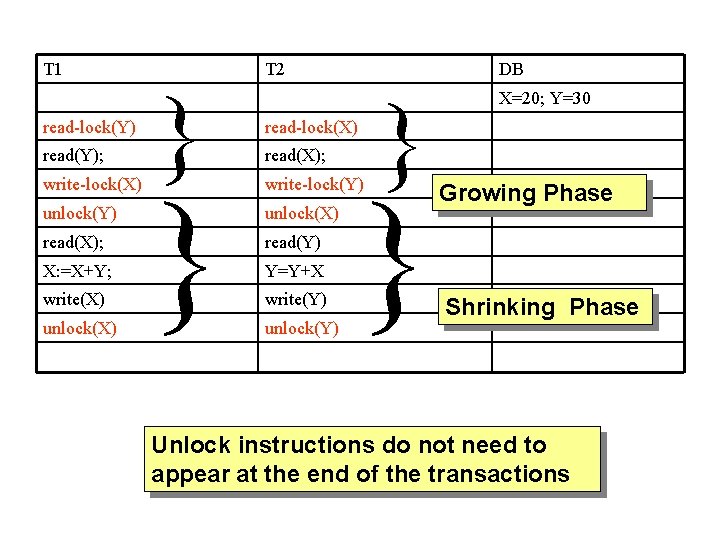
T 1 read-lock(Y) read(Y); write-lock(X) unlock(Y) read(X); X: =X+Y; write(X) unlock(X) } T 2 read-lock(X) read(X); DB } } } write-lock(Y) unlock(X) X=20; Y=30 Growing Phase read(Y) Y=Y+X write(Y) unlock(Y) Shrinking Phase Unlock instructions do not need to appear at the end of the transactions

T 1 read-lock(Y) read(Y); write-lock(X) read(X); X: =X+Y; write(X) unlock(Y) unlock(X) T 2 DB } } X=20; Y=30 read-lock(X) read(X); write-lock(Y) Growing Phase read(Y) Y=Y+X } write(Y) unlock(X) unlock(Y) } Shrinking Phase Deadlocks may occur

2 PL Allows Lock Conversions read_lock(A); read_item(A); read_lock(B); read_item(B); A: = A+B read_lock(C); read_item(C); A: = A+C; . . read_lock(Z); read_item(Z); write_lock(A); A: = A+Z; write(A); unlock(A); . . *upgrade

Concurrency Problems Lost update problem Time T 1 T 2 balx t 1 begin _transaction 100 t 2 begin _transaction read(balx) 100 t 3 read(balx) balx=balx + 100 t 4 balx=balx - 10 write(balx) 200 t 5 write(balx) t 6 commit 90 90 Solution: Prevent T 1 from reading the value of balx until after T 2‘s update has been completed. balx should be 190.

Preventing the lost update problem with 2 PL Time T 1 t 2 T 2 begin _transaction balx 100 write_lock(balx) 100 t 3 write_lock(balx) read (balx) 100 t 4 wait balx=balx +100 t 5 wait write (balx) 200 t 6 wait t 7 read (balx) 200 t 8 balx=balx - 10 200 t 9 write (balx) 190 t 10 commit/unlock(balx) 190 Commit/unlock(balx) 200 Solution: Prevent T 1 from reading the value of balx until after T 2‘s update has been completed.

Concurrency Problems Uncommitted dependency problem Time T 3 T 4 balx t 1 t 2 t 3 begin _transaction read(balx) balx=balx + 100 100 write(balx) … rollback 200 100 t 4 t 5 t 6 begin _transaction read(balx) balx=balx - 10 t 7 t 8 write(balx) commit 190 Solution: Prevent T 3 from reading the value of balx until after the decision has been made to either commit or abort T 4‘s effects; balx should be 90 since T 4 failed.

Preventing the uncommitted dependency problem with 2 PL Time T 3 t 1 T 4 begin _transaction balx 100 t 2 write_lock(balx) 100 t 3 read (balx) 100 balx=balx +100 write (balx) 200 t 4 begin _transaction t 5 write_lock(balx) t 6 wait t 7 read (balx) 100 t 8 balx=balx - 10 100 t 9 write (balx) 90 t 10 commit/unlock(balx) 90 rollback/unlock(balx) 100 Solution: Prevent T 3 from reading the value of balx until after the decision has been made to either commit or abort T 4‘s effects

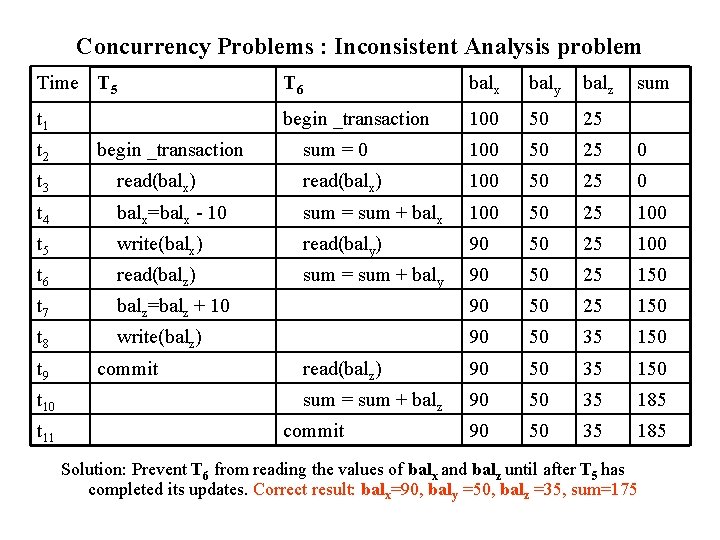
Concurrency Problems : Inconsistent Analysis problem Time T 5 T 6 balx baly balz t 1 begin _transaction 100 50 25 sum = 0 100 50 25 0 t 2 begin _transaction sum t 3 read(balx) 100 50 25 0 t 4 balx=balx - 10 sum = sum + balx 100 50 25 100 t 5 write(balx) read(baly) 90 50 25 100 t 6 read(balz) sum = sum + baly 90 50 25 150 t 7 balz=balz + 10 90 50 25 150 t 8 write(balz) 90 50 35 150 read(balz) 90 50 35 150 sum = sum + balz 90 50 35 185 t 9 t 10 t 11 commit Solution: Prevent T 6 from reading the values of balx and balz until after T 5 has completed its updates. Correct result: balx=90, baly =50, balz =35, sum=175

Preventing the inconsistent analysis problem with 2 PL Time T 5 t 1 t 2 T 6 begin _transaction sum=0 balx baly balz 100 50 25 0 Sum t 3 write_lock(balx) t 4 read (balx) read_lock(balx) 100 50 25 0 t 5 balx=balx - 10 wait 100 50 25 0 t 6 write (balx) wait 90 50 25 0 t 7 write_lock(balz) wait 90 50 25 0 t 8 read (balz) wait 90 50 25 0 t 9 balz=balz + 10 wait 90 50 25 0 t 10 write (balz) wait 90 50 35 0

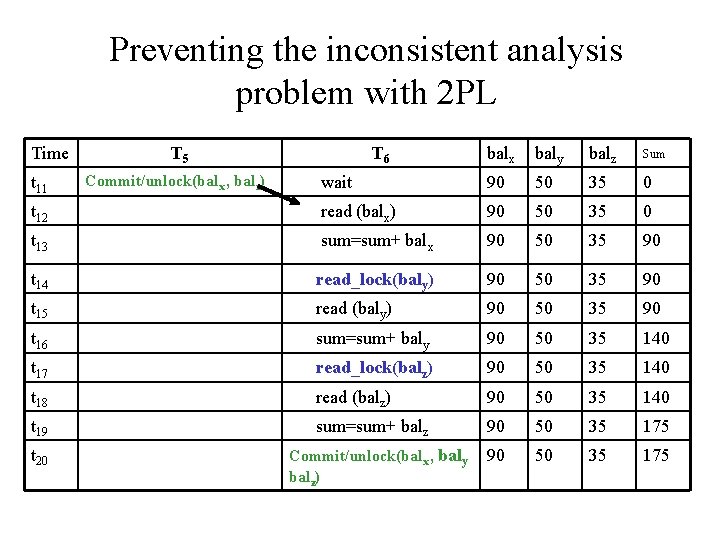
Preventing the inconsistent analysis problem with 2 PL Time balx baly balz Sum wait 90 50 35 0 t 12 read (balx) 90 50 35 0 t 13 sum=sum+ balx 90 50 35 90 t 14 read_lock(baly) 90 50 35 90 t 15 read (baly) 90 50 35 90 t 16 sum=sum+ baly 90 50 35 140 t 17 read_lock(balz) 90 50 35 140 t 18 read (balz) 90 50 35 140 t 19 sum=sum+ balz 90 50 35 175 t 11 t 20 T 5 Commit/unlock(balx , balz) T 6 Commit/unlock(balx , baly balz)

Why 2 PL may reduce concurrency T 1 T 2 DB X=20; Y=30 read-lock(Y) read(Y); write-lock(X) write-lock(Y) read(X); read(Y) X: =X+Y; Y=Y+100 write(X) write(Y) unlock(Y) T 2 waits even though T 1 finishes reading Y unlock(X) • Holding lock unnecessarily, or locking too early: –Transaction T 1 may not be able to release item Y after it is through using it if T 1 must lock an additional item X later on; –or conversely, T 1 must lock the additional item X before it needs it so that it can release Y.

T 1 Why 2 PL may reduce concurrency T 2 DB X=20; Y=30 read-lock(Y) read(Y); write-lock(X) write-lock(Y) read(X); read(Y) X: =X+Y; Y=Y+100 write(X) write(Y) unlock(Y) unlock(X) • Penalty to other transactions: –Another transaction T 2 seeking to access Y may be forced to wait, even though T 1 is done with Y; –conversely, if X is locked earlier than it is needed, another transaction seeking to access X is forced to wait even though T is not using X yet

Variations of 2 PL • • Basic Conservative Strict Rigorous

Conservative 2 PL (static 2 PL) • Requires a transaction to lock all the items it accesses before the transaction begins execution, by predeclaring its read-set and write-set. (The read-set of a transaction is the set of all items that the transaction reads, and the write-set is the set of all items that it writes) • If any of the predeclared items needed cannot be locked, the transaction does not lock any item; instead, it waits until all the items are available for locking.

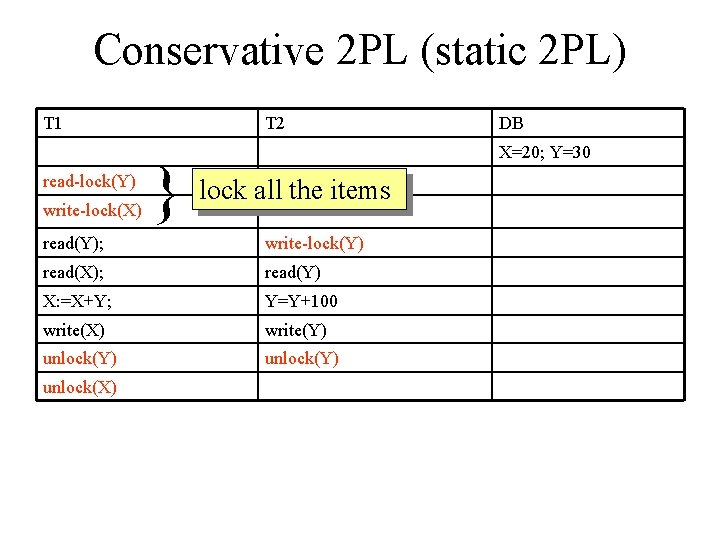
Conservative 2 PL (static 2 PL) T 1 read-lock(Y) write-lock(X) T 2 } lock all the items read(Y); write-lock(Y) read(X); read(Y) X: =X+Y; Y=Y+100 write(X) write(Y) unlock(Y) unlock(X) DB X=20; Y=30

Conservative 2 PL (static 2 PL) • POLICY – lock all that you need before reading or writing. Transaction is in shrinking phase after it starts • PROPERTY – Conservative 2 PL is a deadlock-free protocol • PRACTICAL – difficult to use because of difficulty predeclaring the read-set and write -set.

Strict 2 PL • It is the most popular variation of 2 PL; it guarantees strict schedules. • A transaction T does not release any of its exclusive (write) locks until after it commits or aborts. Hence, no other transaction can read or write an item that is written by T unless T has committed, leading to a strict schedule for recoverability.

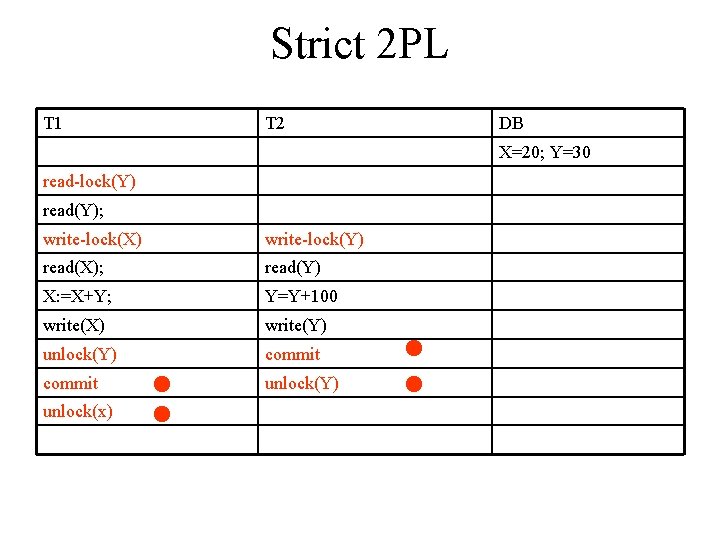
Strict 2 PL T 1 T 2 DB X=20; Y=30 read-lock(Y) read(Y); write-lock(X) write-lock(Y) read(X); read(Y) X: =X+Y; Y=Y+100 write(X) write(Y) unlock(Y) commit unlock(Y) unlock(x)

Strict 2 PL • Policy – release write locks only after terminating. Transaction is in expanding/growing phase until it ends (may release some read locks before commit). • Property – NOT a deadlock-free protocol • PRACTICAL – Possible to enforce and desirable due to recoverability

Rigorous 2 PL • A transaction T does not release any of its locks (exclusive or shared) until after it commits or aborts • Behaves similar to Strict 2 PL except it is more restrictive, but easier to implement since all locks are held till commit.

Rigorous 2 PL T 1 T 2 DB X=20; Y=30 read-lock(Y) read(Y); write-lock(X) write-lock(Y) read(X); read(Y) X: =X+Y; Y=Y+100 write(X) write(Y) commit unlock(X) unlock(Y)

Limitations of 2 PL 1. 2 PL protocol guarantees serializability (that is, every schedule that is permitted is serializable), but it does not permit all possible serializable schedules (that is, some serializable schedules will be prohibited by the protocol). 2. Use of locks can cause two additional problems: deadlock and starvation.

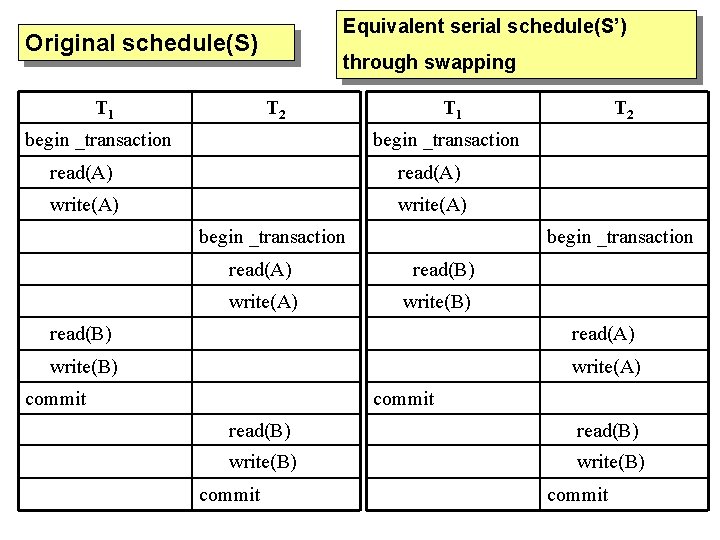
Equivalent serial schedule(S’) Original schedule(S) T 1 through swapping T 2 begin _transaction T 1 T 2 begin _transaction read(A) write(A) begin _transaction read(B) write(B) read(A) write(B) write(A) commit read(B) write(B) commit

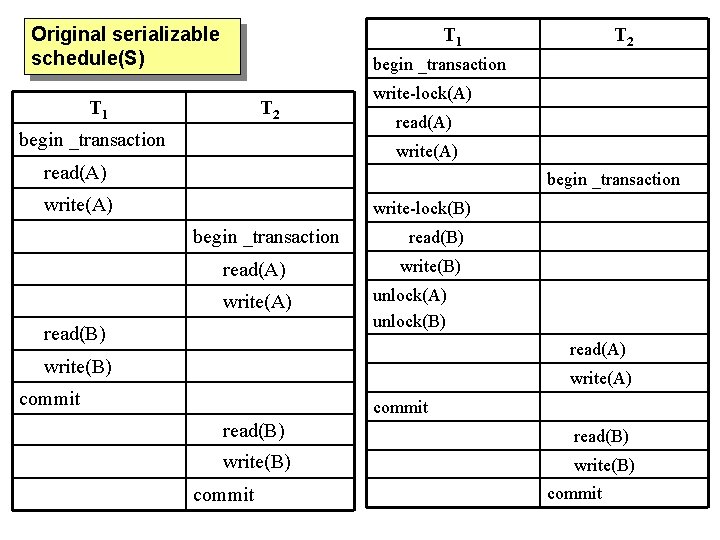
Original serializable schedule(S) T 1 T 2 begin _transaction write-lock(A) read(A) write(A) read(A) begin _transaction write(A) write-lock(B) begin _transaction read(A) write(A) read(B) write(B) unlock(A) unlock(B) read(A) write(B) write(A) commit read(B) write(B) commit

Problems with 2 PL • Deadlock • Livelock / Starvation • Cascading rollback

Problems with 2 PL • Deadlock • Livelock / Starvation • Cascading rollback

Deadlock: Example • Problem: – T 1 adds the content of Y to X; X=X+Y – T 2 adds the content of X to Y; Y=Y+X

Deadlock: Example T 1 T 2 add the content of Y to X of X to Y read_lock(Y); read_lock(X) read_item(Y); write_lock(X); X=X+Y write(X) unlock(Y) read_item(X); write_lock(Y) Y=Y+X write(Y) unlock(X) unlock(Y) Status initial values: X=20, Y =30 Request will be denied since X is locked (shared) to T 2 Request will be denied since Y is locked (shared) to T 1

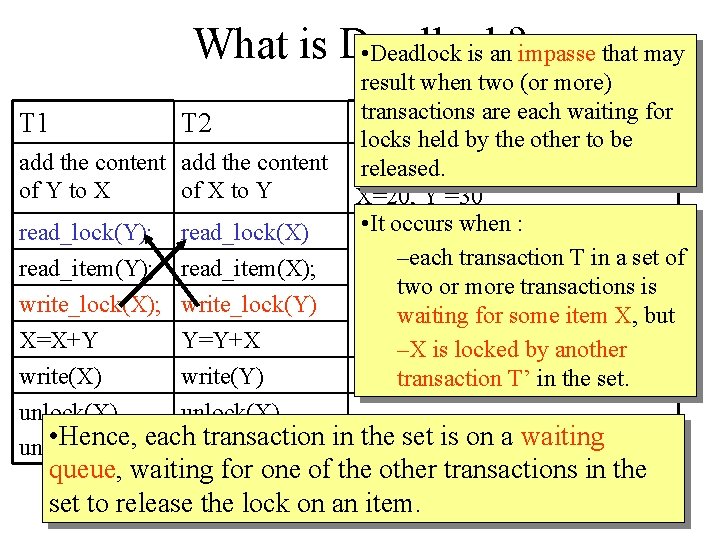
What is Deadlock? • Deadlock is an impasse that may T 1 T 2 add the content of Y to X of X to Y read_lock(Y); read_lock(X) result when two (or more) transactions are each waiting for Status locks held by the other to be initial values: released. X=20, Y =30 • It occurs when : –each transaction T in a set of two or more transactions is waiting for some item X, but –X is locked by another transaction T’ in the set. read_item(Y); read_item(X); write_lock(Y) X=X+Y Y=Y+X write(X) write(Y) unlock(X) • Hence, each transaction in the set is on a waiting unlock(Y) queue, waiting for one of the other transactions in the set to release the lock on an item.

How is Deadlock detected? • Through the construction of wait-for-graph (WFG) showing the transaction dependencies. – Transaction T 1 is dependent on T 2 if transaction T 2 holds the lock on a data item that T 1 is waiting for. • Deadlock exists if and only if the wfg contains a cycle. • The deadlock detection algorithm generates wfg at regular intervals and examines it for a cycle – Small interval: increases overhead – Large interval: deadlock may not de detected for a long period.

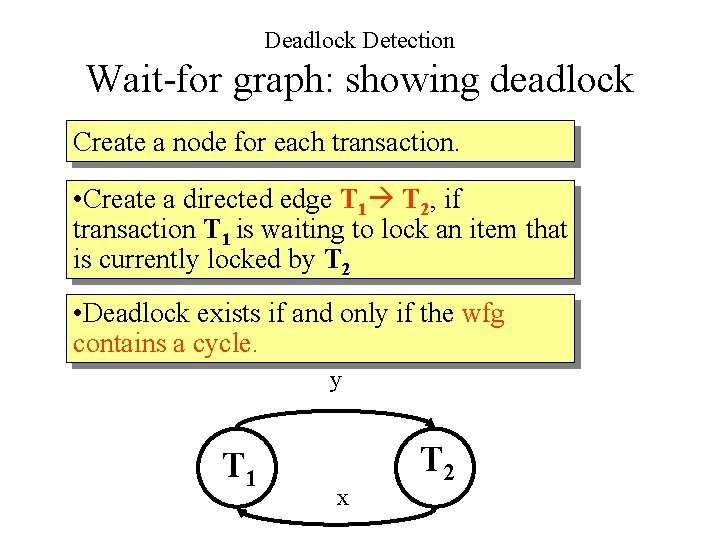
Deadlock Detection Wait-for graph: showing deadlock Create a node for each transaction. • Create a directed edge T 1 T 2, if transaction T 1 is waiting to lock an item that is currently locked by T 2 • Deadlock exists if and only if the wfg contains a cycle. y T 1 x T 2

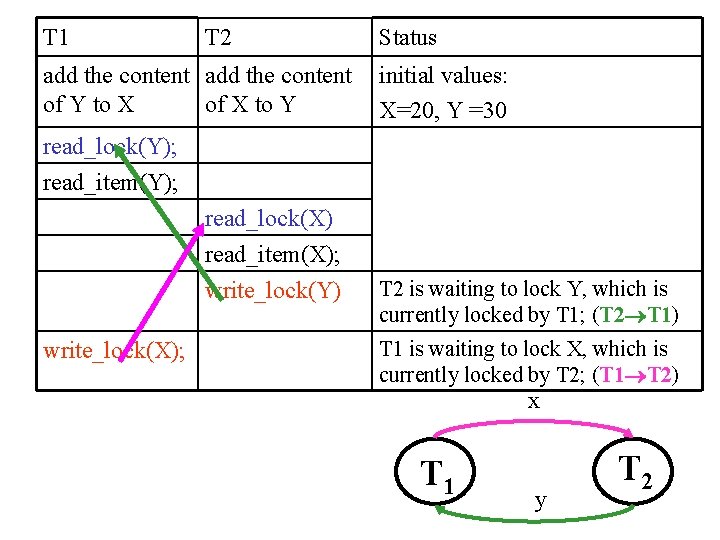
T 1 T 2 add the content of Y to X of X to Y Status initial values: X=20, Y =30 read_lock(Y); read_item(Y); read_lock(X) read_item(X); write_lock(Y) write_lock(X); T 2 is waiting to lock Y, which is currently locked by T 1; (T 2 T 1) T 1 is waiting to lock X, which is currently locked by T 2; (T 1 T 2) x T 1 y T 2

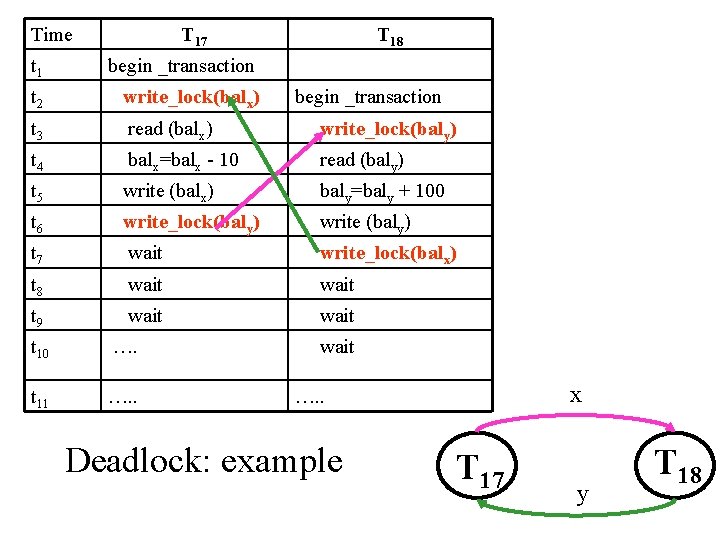
Time T 17 T 18 t 1 begin _transaction t 2 write_lock(balx) t 3 read (balx) write_lock(baly) t 4 balx=balx - 10 read (baly) t 5 write (balx) baly=baly + 100 t 6 write_lock(baly) write (baly) t 7 wait write_lock(balx) t 8 wait t 9 wait t 10 …. t 11 …. . begin _transaction wait x …. . Deadlock: example T 17 y T 18

How is deadlock solved? T 17 T 18 t 1 begin _transaction t 2 write_lock(balx) t 3 read (balx) t 4 balx=balx - 10 t 5 write (balx) t 6 write_lock(baly) t 7 wait t 8 wait t 9 wait t 10 …. t 11 …. . • Break deadlock by aborting one or more of the transactions • Abort transaction T 18 begin _transaction • Locks held by T 18 are write_lock(baly) released read (baly) • Transaction T 17 can baly=baly + 100 continue and finish write (baly) • DBMS restarts T 18 write_lock(balx) wait …. .

How is Deadlock Handled? • Deadlock prevention – The DBMS looks ahead to determine if a transaction would cause deadlock and never allows deadlock to occur. • Deadlock detection and recovery – The DBMS allows deadlock to occur but recognizes occurrences of deadlock and breaks it.

Deadlock Prevention 1. 2. 3. 4. 5. 6. Use of Conservative Locking Ordering of all items in the database … Use of transaction timestamp No waiting Cautious waiting Use of timeouts

Deadlock Prevention Use of Conservative Locking T 17 T 18 begin _transaction • Every transaction locks all the items it needs in advance (generally not a practical assumption) write_lock(X) write_lock(Y) begin _transaction read (X) write_lock(Y) X=X - 10 write_lock(X) write (X) read (Y) … unlock(X) Y=Y + 100 unlock(Y) write (Y) … unlock(Y) unlock(X) • If any of the items cannot be obtained, none of the items are locked. Rather, the transaction waits and then tries again to lock all the item it needs.

Review: Conservative 2 PL (static 2 PL) • Requires a transaction to lock all the items it accesses before the transaction begins execution, by predeclaring its read-set and write-set. (The read-set of a transaction is the set of all items that the transaction reads, and the write-set is the set of all items that it writes) • If any of the predeclared items needed cannot be locked, the transaction does not lock any item; instead, it waits until all the items are available for locking.

Deadlock Prevention Ordering of all items in the database… T 17 T 18 begin _transaction write_lock(X) begin _transaction read (X) write_lock(X) X=X - 10 read (X) write (X) X=X+ 100 write_lock(Y) write (Y) … … X Y Z • Ordering all the items in the database and making sure that a transaction that needs several items will lock them according to that order. • However, this requires that the programmer is aware of the chosen order of the items, which is not very practical

Deadlock Prevention No Waiting • In case of inability to obtain a lock, a transaction aborts and is resubmitted with a fixed delay. (causes too many needless aborts)

Deadlock Prevention Cautious Waiting Suppose that transaction Ti tries to lock an item X but is not able to do so because X is locked by some other transaction Tj with a conflicting lock. (Ti Tj) Cautious waiting: if Tj is not blocked (not waiting for some other locked item) then Ti is blocked and allowed to wait else abort Ti That is, if Ti is waiting for Tj, let Ti wait unless Tj is also waiting for Tz to release some other item.

Deadlock Prevention Cautious Waiting Time t 1 Ti Tj begin _transaction t 2 write_lock(balx) begin _transaction t 3 read (balx) write_lock(baly) t 4 balx=balx - 10 read (baly) t 5 write (balx) baly=baly + 100 t 6 write_lock(baly) write (baly) t 7 wait …. t 8 wait t 9 wait Since Tj is not blocked (not waiting for some other locked item) then Ti is blocked and allowed to wait

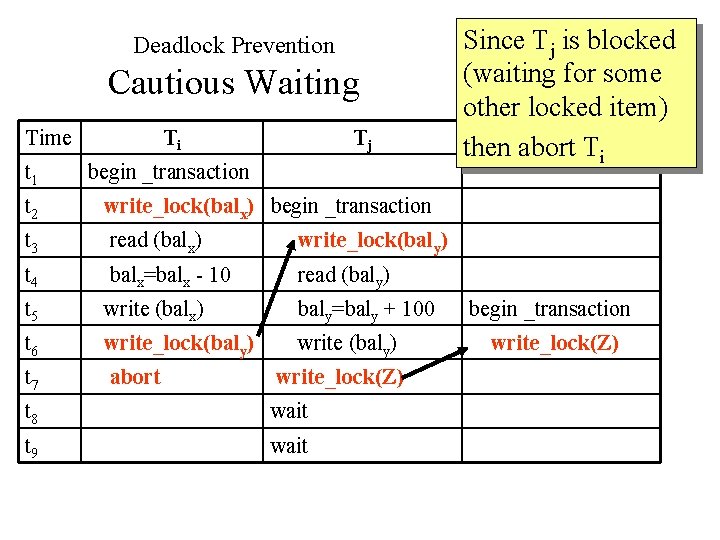
Deadlock Prevention Cautious Waiting Time t 1 Ti Tj begin _transaction t 2 write_lock(balx) begin _transaction t 3 read (balx) write_lock(baly) t 4 balx=balx - 10 read (baly) t 5 write (balx) baly=baly + 100 t 6 write_lock(baly) write (baly) t 7 abort write_lock(Z) t 8 wait t 9 wait Since Tj is blocked (waiting for some other locked item) Tk then abort Ti begin _transaction write_lock(Z)

Deadlock Prevention Use of Timeouts • Practical because of its low overhead and simplicity. • If a transaction waits for a period longer than a system-defined timeout period, the system assumes that the transaction may be deadlocked and aborts it – regardless of whether a deadlock actually exists or not. • DISADVANTAGE: Some transactions that were not deadlocked may abort and may have to be resubmitted.

Deadlock Prevention Use of transaction timestamp • Use of a transaction timestamp TS(T), which is a unique identifier assigned to each transaction. • The timestamps are typically ordered based on the order in which transactions are started; hence, if T 1 starts before transaction T 2, then TS(T 1) < TS(T 2) • The older transaction T 1 has the smaller timestamp value

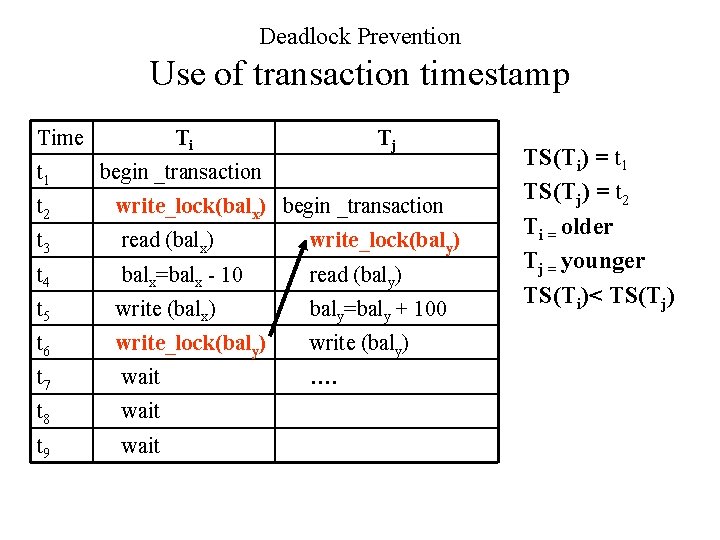
Deadlock Prevention Use of transaction timestamp Time t 1 Ti Tj begin _transaction t 2 write_lock(balx) begin _transaction t 3 read (balx) write_lock(baly) t 4 balx=balx - 10 read (baly) t 5 write (balx) baly=baly + 100 t 6 write_lock(baly) write (baly) t 7 wait …. t 8 wait t 9 wait TS(Ti) = t 1 TS(Tj) = t 2 Ti = older Tj = younger TS(Ti)< TS(Tj)

Two Schemes of Deadlock Prevention • Wait-die • Wound-wait Case: Suppose the transaction Ti tries to lock an item X, but is not able to because X is locked by some other transaction Tj with a conflicting lock. Ti Tj , therefore Ti is waiting for Tj

Two Schemes of Deadlock Prevention Wait-Die : Ti Tj The rules of wait-die are as follows: if TS(Ti) < TS(Tj) then (Ti older than Tj) Ti is allowed to wait else (Ti younger than Tj) abort Ti (Ti dies) and restart it later with the same timestamp • Older transactions producing deadlock waits on younger transaction to get the locked items held by it. • Younger transaction producing deadlock gives up the wait and aborts (dies), then gets resubmitted.

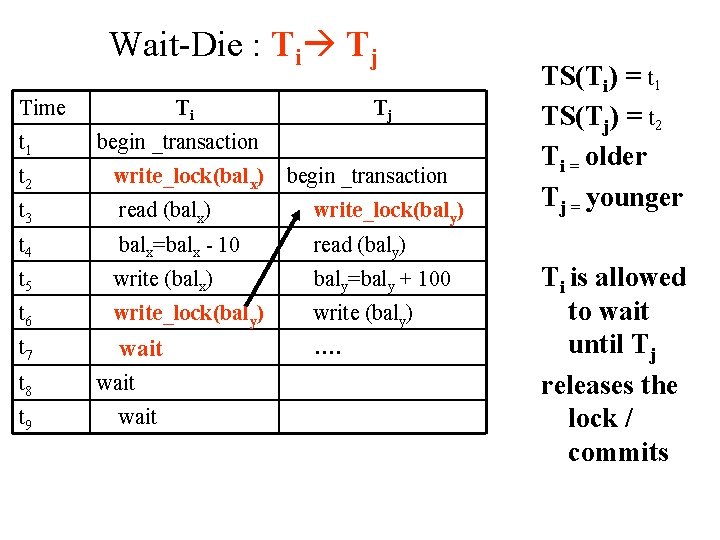
Wait-Die : Ti Tj Time Ti Tj t 1 begin _transaction t 2 write_lock(balx) t 3 read (balx) write_lock(baly) t 4 balx=balx - 10 read (baly) t 5 write (balx) baly=baly + 100 t 6 write_lock(baly) write (baly) t 7 wait …. t 8 t 9 wait begin _transaction TS(Ti) = t 1 TS(Tj) = t 2 Ti = older Tj = younger Ti is allowed to wait until Tj releases the lock / commits

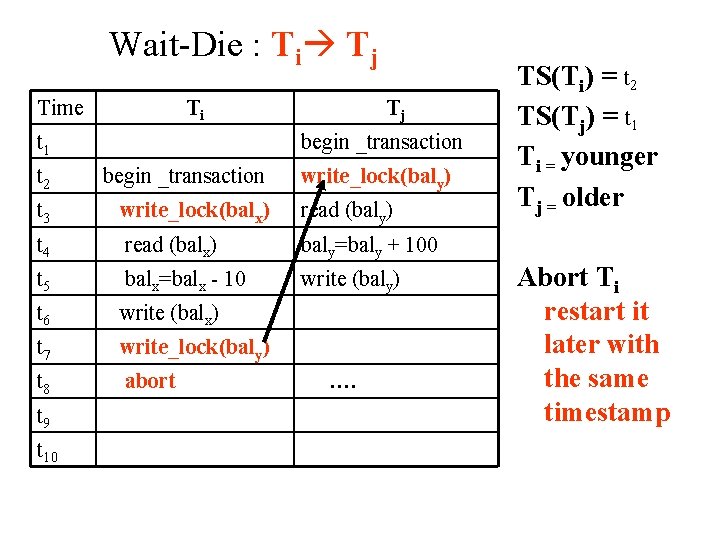
Wait-Die : Ti Tj Time Ti t 1 Tj begin _transaction t 2 begin _transaction t 3 write_lock(balx) read (baly) t 4 read (balx) baly=baly + 100 t 5 balx=balx - 10 write (baly) t 6 write (balx) t 7 write_lock(baly) t 8 abort t 9 t 10 write_lock(baly) …. TS(Ti) = t 2 TS(Tj) = t 1 Ti = younger Tj = older Abort Ti restart it later with the same timestamp

Two Schemes of Deadlock Prevention Wound-Wait: Ti Tj The rules of wound-wait are as follows: If TS(Ti) < TS(Tj) Then (Ti older than Tj) abort Tj (Ti wounds Tj) and restart it later with the same timestamp Else (Ti younger than Tj) Ti is allowed to wait • Younger transaction producing deadlock allowed to wait for older one to release locked item • Older transaction producing deadlock preempts the younger transaction by wounding (killing) it and causing it to abort.

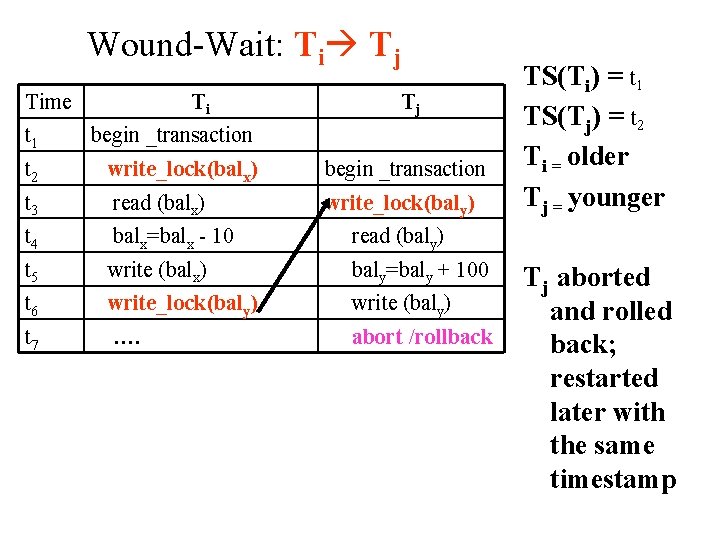
Wound-Wait: Ti Tj Time Ti Tj t 1 begin _transaction t 2 write_lock(balx) begin _transaction t 3 read (balx) write_lock(baly) t 4 balx=balx - 10 read (baly) t 5 write (balx) baly=baly + 100 t 6 write_lock(baly) write (baly) t 7 …. abort /rollback TS(Ti) = t 1 TS(Tj) = t 2 Ti = older Tj = younger Tj aborted and rolled back; restarted later with the same timestamp

Wound-Wait: Ti Tj Time Ti t 1 Tj begin _transaction t 2 begin _transaction t 3 write_lock(balx) read (baly) t 4 read (balx) baly=baly + 100 t 5 balx=balx - 10 write (baly) t 6 write (balx) t 7 write_lock(baly) t 8 wait t 9 t 10 write_lock(baly) …. TS(Ti) = t 2 TS(Tj) = t 1 Ti = younger Tj = older Ti is allowed to wait

Two Schemes of Deadlock Prevention Wait-Die and Wound-Wait Both schemes kill younger transactions involved in a deadlock. Wait-die: transactions only wait on younger transactions Wound-wait: transactions only wait on older transactions Both schemes are deadlock-free.

Problems with 2 PL • Deadlock • Livelock / Starvation • Cascading rollback

Livelock/Starvation 1. A transaction is starved if it cannot proceed for an indefinite period of time while other transactions in the system continue normally. This may occur if the waiting scheme for locked items is unfair, giving priority to some transactions over others.

Livelock/Starvation 2. Starvation can only occur in the algorithms for dealing with deadlock. It occurs if the algorithms select the same transaction as victim repeatedly, thus causing it to abort and never finish execution.

Remedies for Preventing Starvation 1. First-come-first-serve queue • • a fair waiting scheme; transactions are enabled to lock an item in the order in which they are originally requested to lock the item. 2. Allow some transactions to have priority over others but increase the priority of a transaction the longer it waits, until it eventually gets the highest priority and proceeds.

Remedies for Preventing Starvation 3. The victim selection algorithm can use higher priorities for transactions that have been aborted multiple times so that they are not selected as victims repeatedly. The wait-die and wound-wait schemes avoid starvation.

Problems with 2 PL • Deadlock • Livelock / Starvation • Cascading rollback

Problems with 2 PL Cascading Rollback • Cascading rollback occurs when a single transaction leads to a series of rollbacks. • Cascading rollbacks are undesirable since they potentially lead to the undoing of a significant amount of work

Cascading rollback in 2 PL Time t 1 T 14 begin _transaction t 2 write_lock(balx) t 3 read (balx) t 4 read_lock(baly) t 5 read (baly) t 6 balx=baly + balx t 7 write (balx) t 8 unlock (balx) t 9 t 10 T 15 . . . begin _transaction write_lock(balx) read (balx) T 16

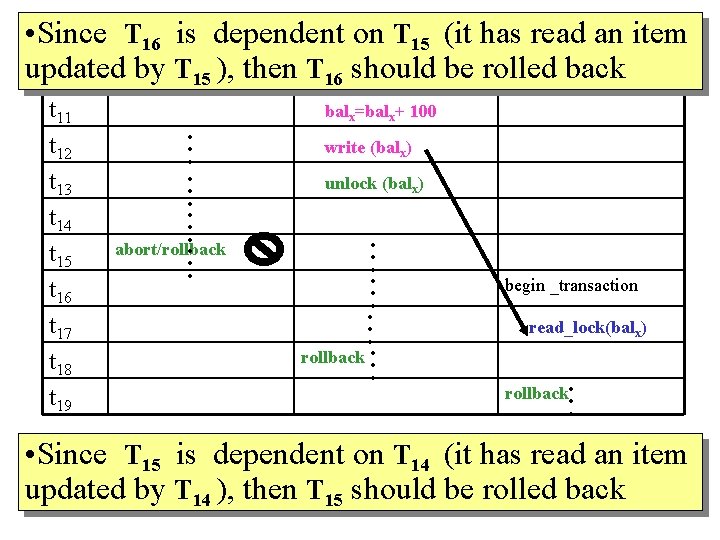
• Since T 16 Cascading is dependentrollback on T 15 (itin has 2 PL read an item updated Time by TT 1514), then T 16 should T 15 be rolled back T 16 t 11 t 12 t 13 t 14 t 15 t 16 t 17 t 18 t 19 . . . abort/rollback. balx=balx+ 100 write (balx) unlock (balx) . . rollback. . begin _transaction read_lock(balx) rollback. . . • Since T 15 is dependent on T 14 (it has read an item updated by T 14 ), then T 15 should be rolled back

Cascading rollback in 2 PL • Cascading rollback happens when a single transaction leads to a series of rollback. Failure (and rollback) of T 14 results in T 15 and T 16 being rolled back

How to prevent cascading rollbacks? • Leave the release of all locks until the end of the transaction (rigorous 2 PL). • This prevents other transactions to read values of items whose transactions have not yet committed.