CONCEPTUAL ARITHMETIC METHODS WITH DECIMALS Multiplication Multiplication with

CONCEPTUAL ARITHMETIC METHODS WITH DECIMALS Multiplication

Multiplication with decimals The following three techniques will be covered in this presentation: �Using upper and lower product bounds to correctly place the decimal point �Converting �Place to fractions value multiplication

Technique 1 Using upper and lower product bounds to correctly place the decimal point

Example 1: Find the product of 3. 8 and 0. 52 1. Find upper and lower bounds for the factors: 3 < 3. 8 < 4 and 0. 5 < 0. 52 < 0. 6 2. Find upper and lower bounds for the product:

Example 1: Find the product of 3. 8 and 0. 52 3. Multiply the factors as if they were whole numbers: 4. Use the upper and lower bounds for the product to correctly place the decimal point. Answer:

Example 2: Find the product of 72. 3 and 8. 201 1. 70 < 72. 3 < 80 and 2. 8 < 8. 201 < 9 3. Multiply the factors as if they were whole numbers: 4. Correctly place the decimal point using the bounds.

Technique 2 Convert to fractions

Example 3: Find the product of 1. 2 and 0. 03 1. Convert each decimal to fraction form: 2. Multiply the fractions: 1. Rewrite in decimal form: 1. 2 x 0. 03 = 0. 036 If you have trouble seeing the decimal form, note that 36/1000 = 30/1000 + 6/1000 = 3/100 + 6/1000 = 0. 03 + 0. 006 = 0. 036

Example 4: Find the product of 0. 025 and 0. 08 1. Convert each decimal to fraction form: 2. Multiply the fractions: 1. Rewrite in decimal form: 0. 025 x 0. 08 = 0. 002

Example 5: Find the product of 34. 23 and 0. 011 1. Convert each decimal to fraction form: 2. Multiply the fractions: 1. Rewrite in decimal form: 34. 23 x 0. 011 = 0. 37653 Note that the final digit of 3 in the numerator 37653 from step 2 must be in the 100, 000 ths (hundred thousandths) place.

Technique 3 Place Value Multiplication

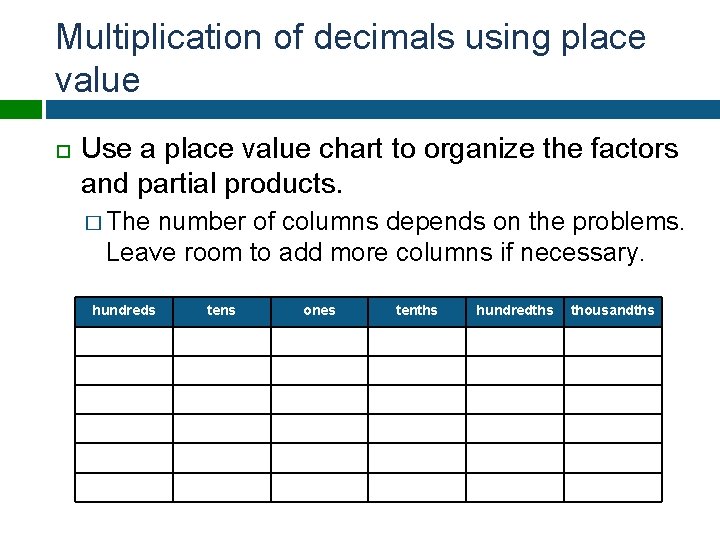
Multiplication of decimals using place value Use a place value chart to organize the factors and partial products. � The number of columns depends on the problems. Leave room to add more columns if necessary. hundreds tens ones tenths hundredths thousandths

Example 6: Find the product of 2. 3 and 4. 5 Step 1: Enter the factors into a place value chart. tens ones tenths hundredths reasoning 2 3 2 ones and 3 tenths 4 5 4 ones and 5 tenths

Example 6: Find the product of 2. 3 and 4. 5 Step 2: Find the partial products. tens ones tenths 2 3 2 ones and 3 tenths 4 5 4 ones and 5 tenths 1 hundredths 5 reasoning

Example 6: Find the product of 2. 3 and 4. 5 Step 2: Find the partial products. tens ones tenths 2 3 2 ones and 3 tenths 4 5 4 ones and 5 tenths 1 1 0 hundredths 5 reasoning

Example 6: Find the product of 2. 3 and 4. 5 Step 2: Find the partial products. tens ones tenths 2 3 2 ones and 3 tenths 4 5 4 ones and 5 tenths 1 1 0 1 2 hundredths 5 reasoning

Example 6: Find the product of 2. 3 and 4. 5 Step 2: Find the partial products. tens ones tenths 2 3 2 ones and 3 tenths 4 5 4 ones and 5 tenths 1 1 0 1 2 8 hundredths 5 reasoning

Example 6: Find the product of 2. 3 and 4. 5 Step 3: Sum the partial products to obtain the final product. tens ones tenths hundredths reasoning 2 3 2 ones and 3 tenths 4 5 4 ones and 5 tenths 1 1 0 1 2 5 8 1 0 3 5 2. 3 x 4. 5 = 10. 35

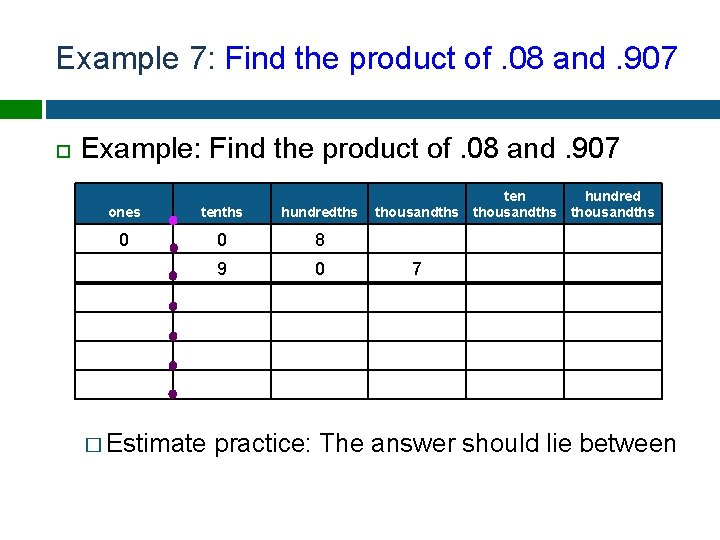
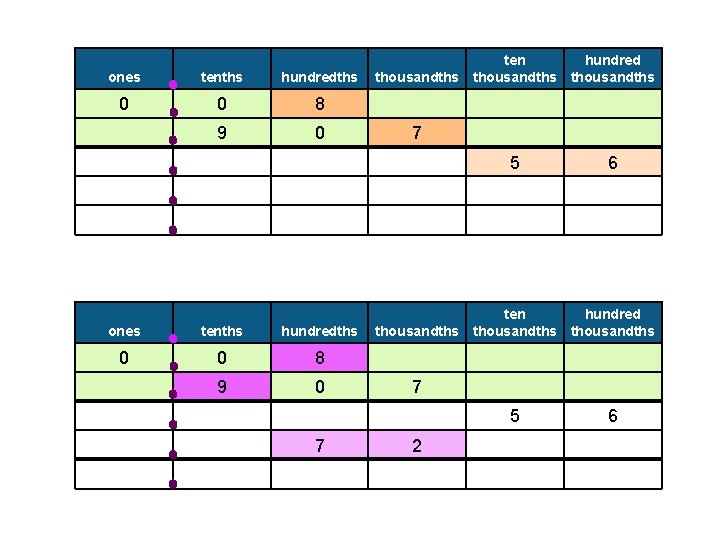
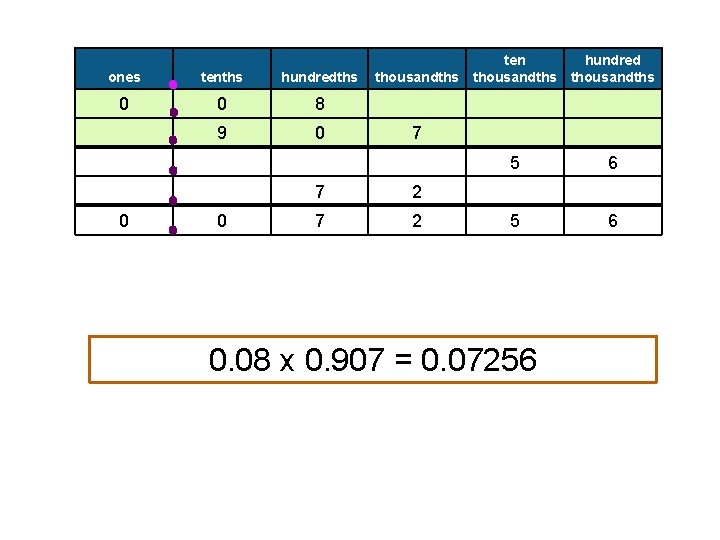
Example 7: Find the product of. 08 and. 907 Example: Find the product of. 08 and. 907 ones tenths hundredths 0 0 8 9 0 � Estimate ten hundred thousandths 7 practice: The answer should lie between

ones tenths hundredths 0 0 8 9 0 ten hundred thousandths thousandths 7 5 7 6 2 6

ones tenths hundredths 0 0 8 9 0 0 0 ten hundred thousandths 7 7 2 5 6 0. 08 x 0. 907 = 0. 07256

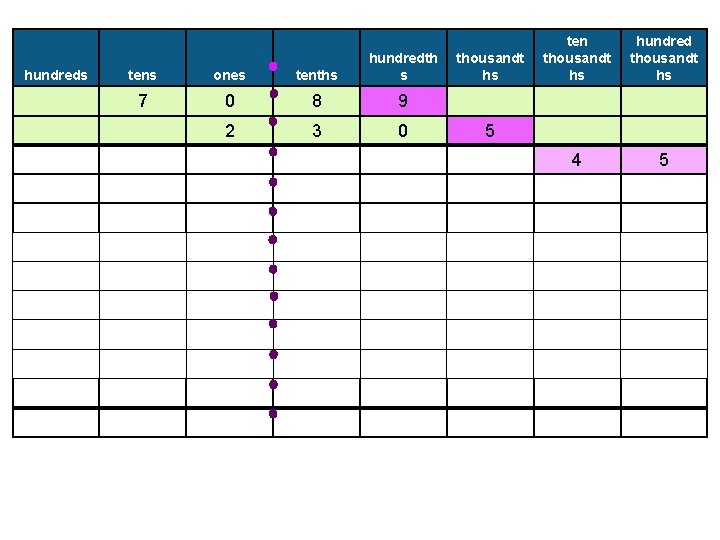
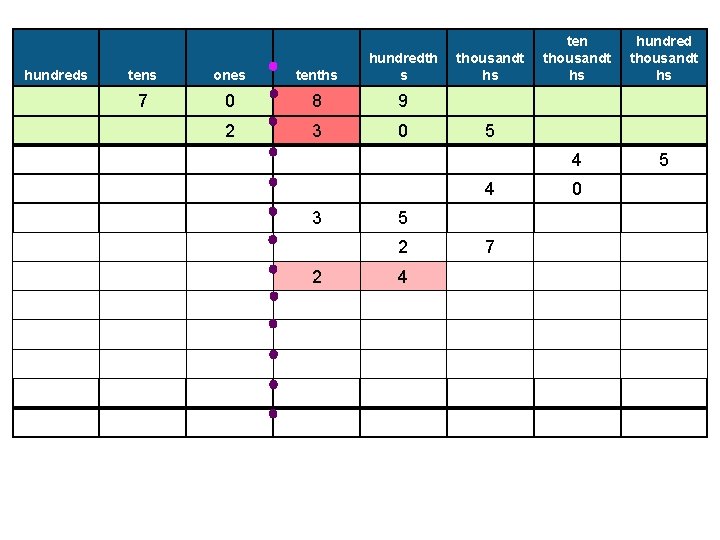
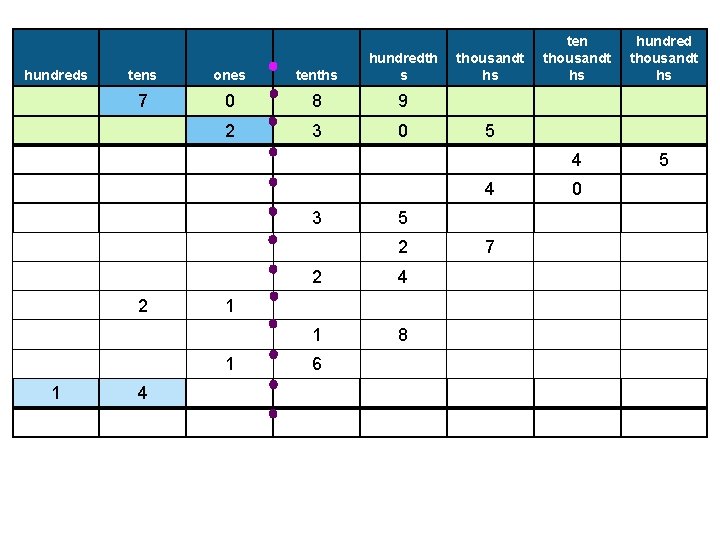
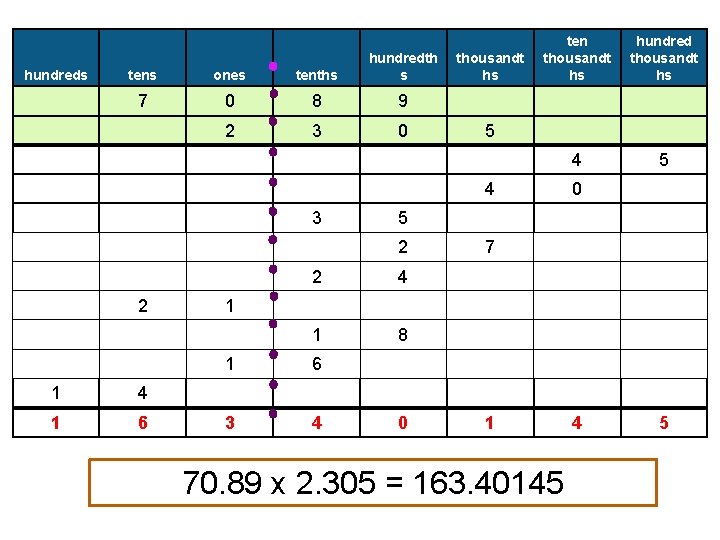
Example 8: Find the product of 2. 305 and 70. 89. � Estimating, we see that our answer should be between 2 x 70 = 140 and 3 x 71 = 213. We can use this as a check at the end.

hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs ten thousandt hs hundred thousandt hs 4 5 5

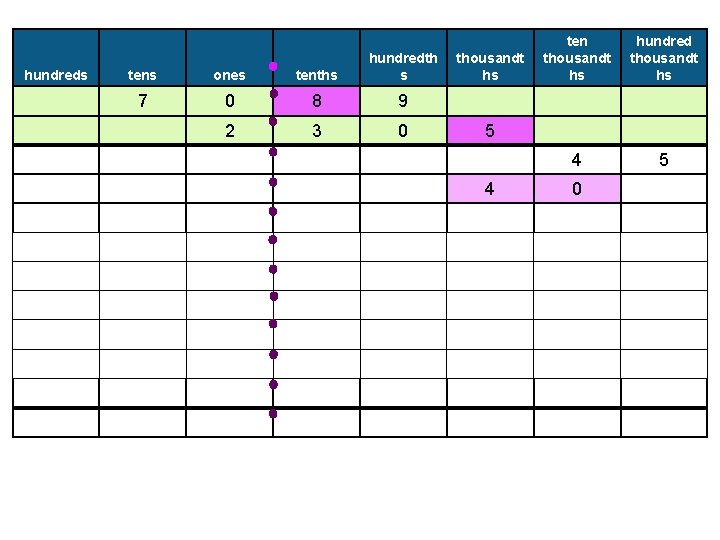
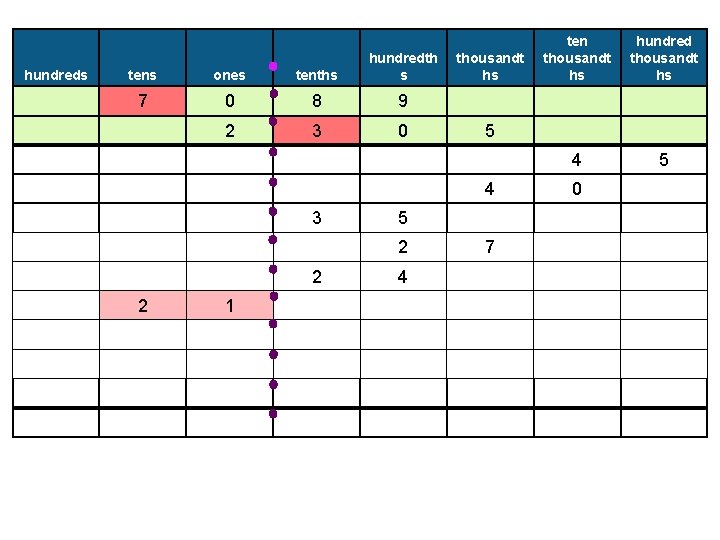
hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs ten thousandt hs hundred thousandt hs 4 5 5 4 0

hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs 5 hundred thousandt hs 4 5 5 4 3 ten thousandt hs 0

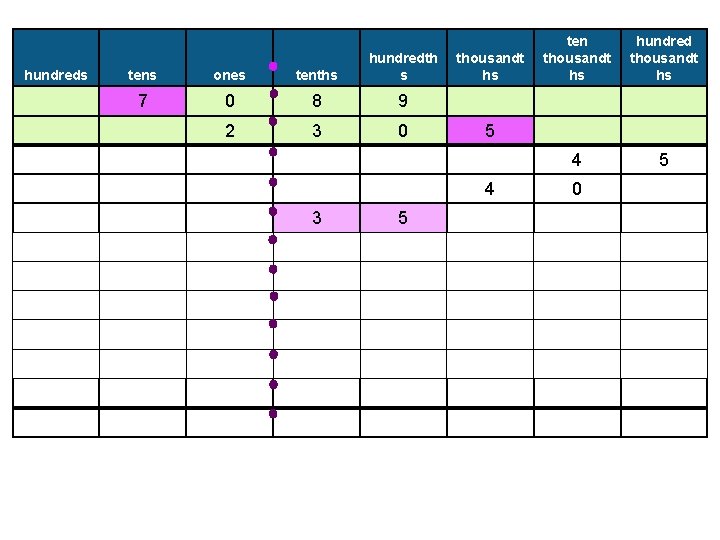
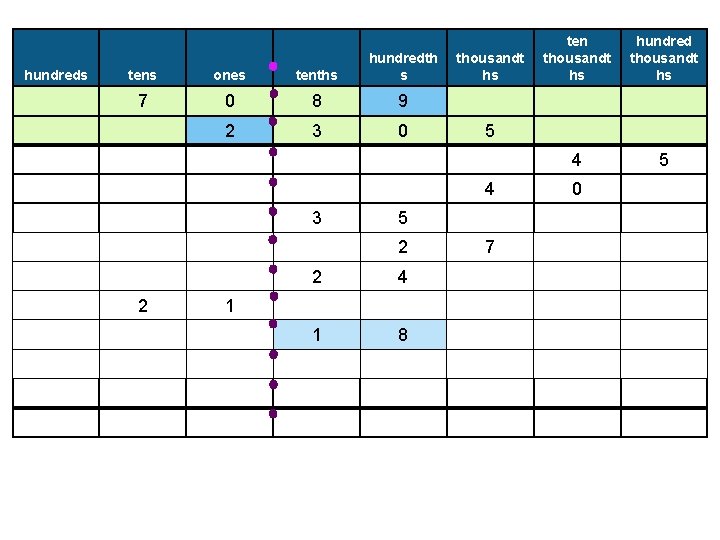
hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs 5 2 hundred thousandt hs 4 5 5 4 3 ten thousandt hs 7 0

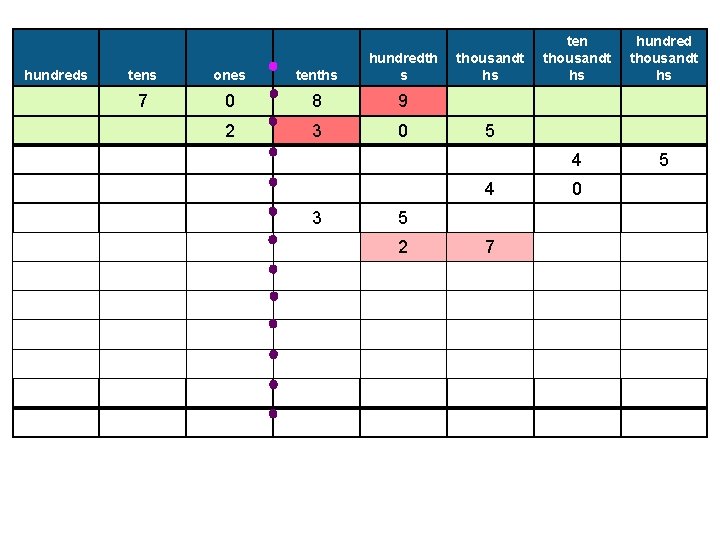
hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs 5 2 2 4 hundred thousandt hs 4 5 5 4 3 ten thousandt hs 7 0

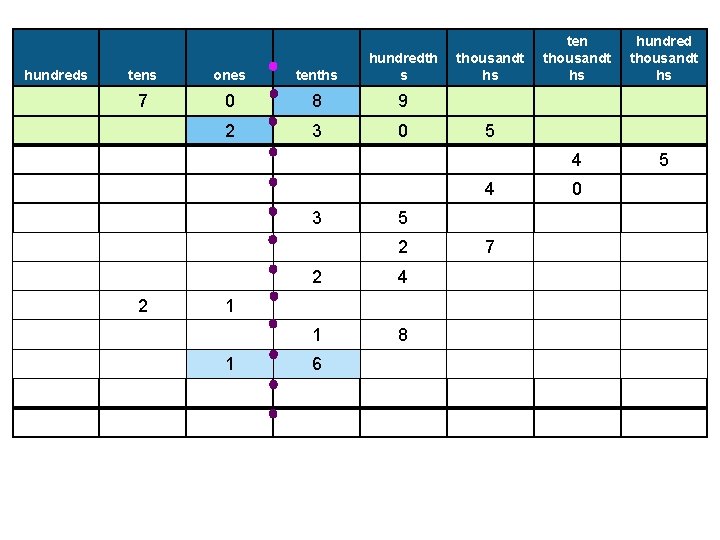
hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs 5 2 2 2 1 4 hundred thousandt hs 4 5 5 4 3 ten thousandt hs 7 0

hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs 5 2 2 2 4 1 8 1 hundred thousandt hs 4 5 5 4 3 ten thousandt hs 7 0

hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs 5 2 2 2 4 1 8 1 1 6 hundred thousandt hs 4 5 5 4 3 ten thousandt hs 7 0

hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs 5 2 2 4 4 1 8 1 1 1 2 6 hundred thousandt hs 4 5 5 4 3 ten thousandt hs 7 0

hundreds tens ones tenths hundredth s 7 0 8 9 2 3 0 thousandt hs ten thousandt hs hundred thousandt hs 4 5 5 4 3 5 2 2 1 4 1 6 0 2 4 1 8 7 1 1 6 3 4 0 1 70. 89 x 2. 305 = 163. 40145 4 5