Concepts Scatter Plot Correlation positive negative none weak

Concepts • Scatter Plot • Correlation: positive, negative, none; weak, strong, perfect, significant • Regression • Rank correlation • Prediction interval

Skills • Creating and interpreting a scatter plot • Finding and interpreting the regression coefficient – Determining if the regression coefficient is significant • Writing and using the regression equation – Deciding when to use the mean and when to use the regression equation for as a point estimate of y for a given x • Find and interpreting the rank regression coefficient. – Determining if the rank regression coefficient is significant • Creating a prediction interval

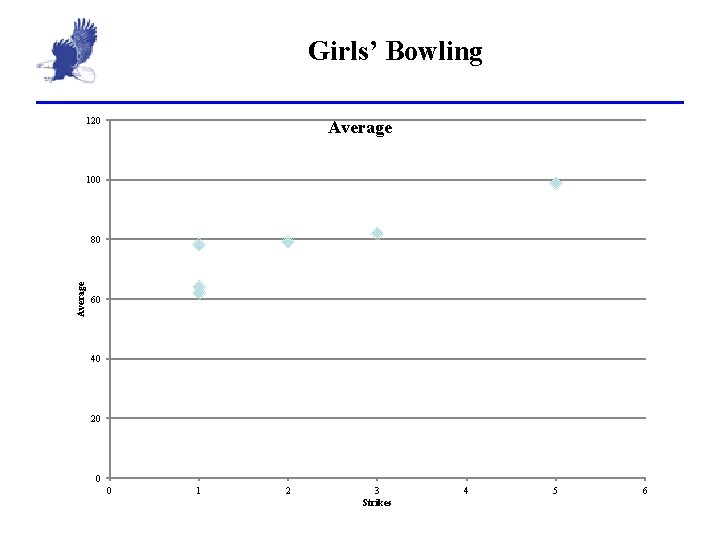
Problem: Girls Bowling Strikes 3 5 1 1 1 2 Average 82 99 64 62 78 79 1. Draw and interpret a scatter chart. 2. Find the regression coefficient for the correlation between the number of strikes and the average bowling score. 1. Describe the meaning of the correlation 2. 3. Is this what you expected? If not, why not? . Determine of the correlation is significant. 3. Write the regression equation 4. What is the point estimate of the average of a bowler who rolled 4 strikes? 5. What is the prediction interval of the average of a bowler who rolled 4 strikes?

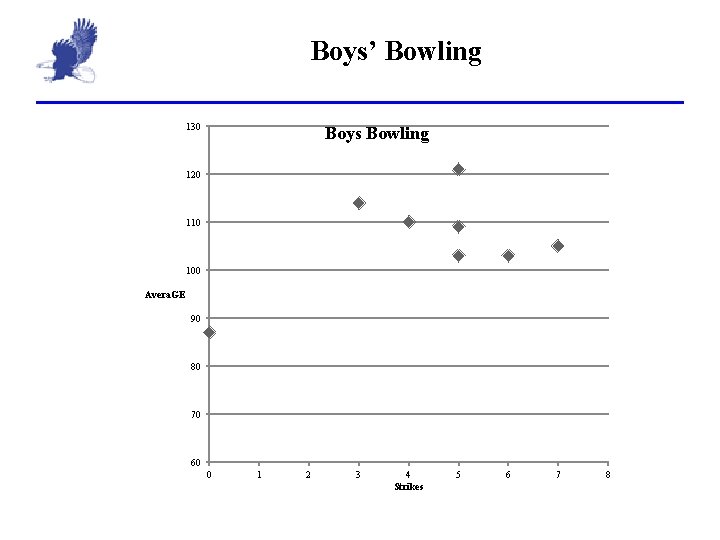
Problem: Boys Bowling Strikes Average 3 6 5 5 7 0 4 5 114 103 109 105 87 110 121 1. Draw and interpret a scatter chart 2. Find the regression coefficient for the correlation between the number of strikes and the average score. 1. Describe the meaning of the correlation 2. Is this what you expected? If not, why not? . 3. Determine if the correlation is significant. 3. Write the regression equation 4. Estimate of the average of a bowler who rolled 2 strikes 1. Explain why you choose the particular value.

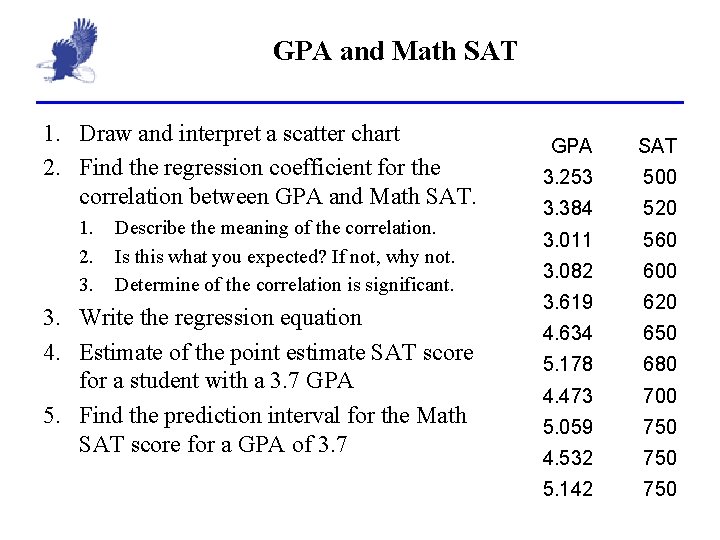
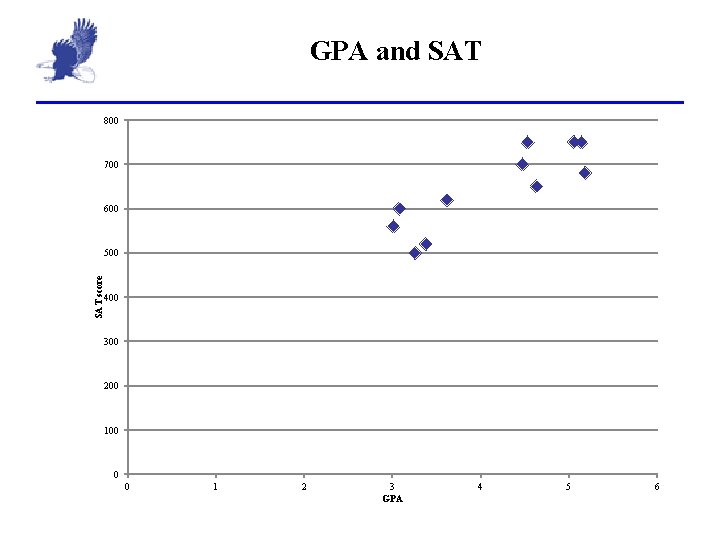
GPA and Math SAT 1. Draw and interpret a scatter chart 2. Find the regression coefficient for the correlation between GPA and Math SAT. 1. 2. 3. Describe the meaning of the correlation. Is this what you expected? If not, why not. Determine of the correlation is significant. 3. Write the regression equation 4. Estimate of the point estimate SAT score for a student with a 3. 7 GPA 5. Find the prediction interval for the Math SAT score for a GPA of 3. 7 GPA SAT 3. 253 500 3. 384 520 3. 011 560 3. 082 600 3. 619 620 4. 634 650 5. 178 680 4. 473 700 5. 059 750 4. 532 750 5. 142 750

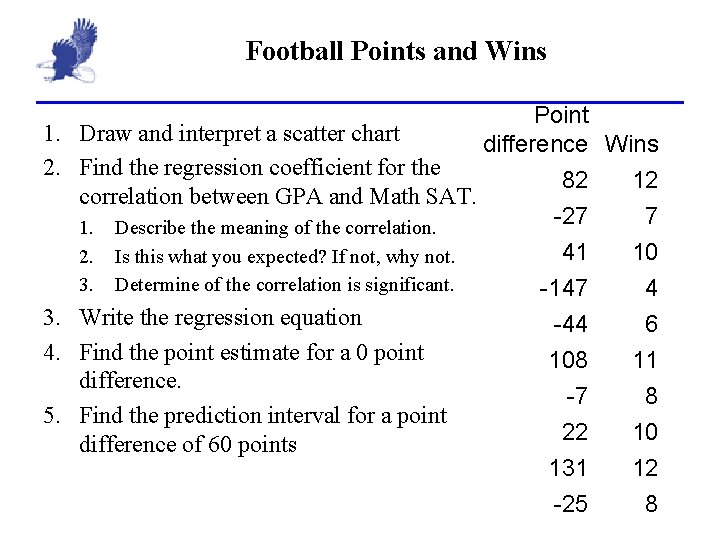
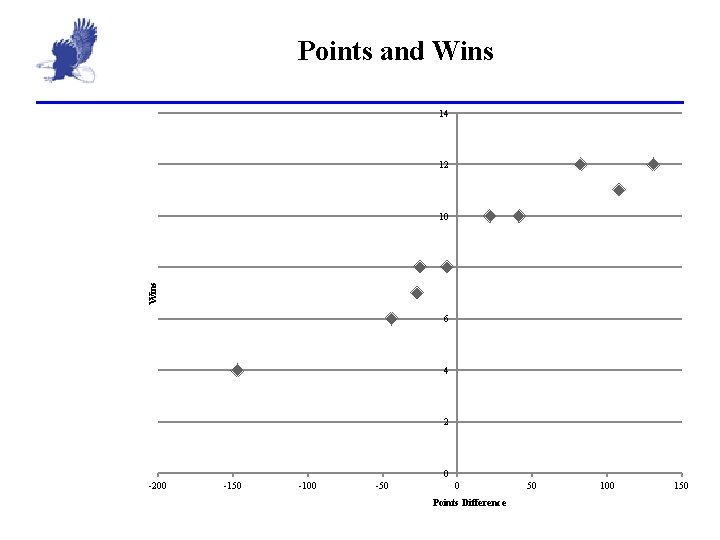
Football Points and Wins Point 1. Draw and interpret a scatter chart difference Wins 2. Find the regression coefficient for the 82 12 correlation between GPA and Math SAT. -27 7 1. Describe the meaning of the correlation. 2. 3. Is this what you expected? If not, why not. Determine of the correlation is significant. 3. Write the regression equation 4. Find the point estimate for a 0 point difference. 5. Find the prediction interval for a point difference of 60 points 41 -147 -44 108 -7 22 131 -25 10 4 6 11 8 10 12 8

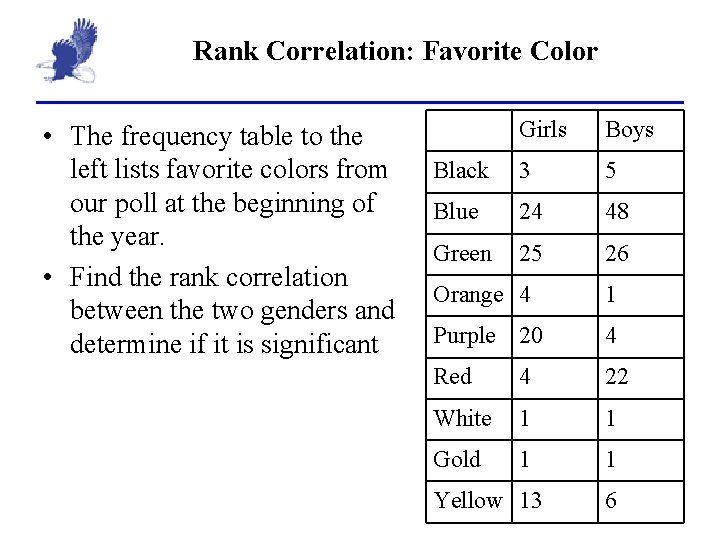
Rank Correlation: Favorite Color • The frequency table to the left lists favorite colors from our poll at the beginning of the year. • Find the rank correlation between the two genders and determine if it is significant Girls Boys Black 3 5 Blue 24 48 Green 25 26 Orange 4 1 Purple 20 4 Red 4 22 White 1 1 Gold 1 1 Yellow 13 6

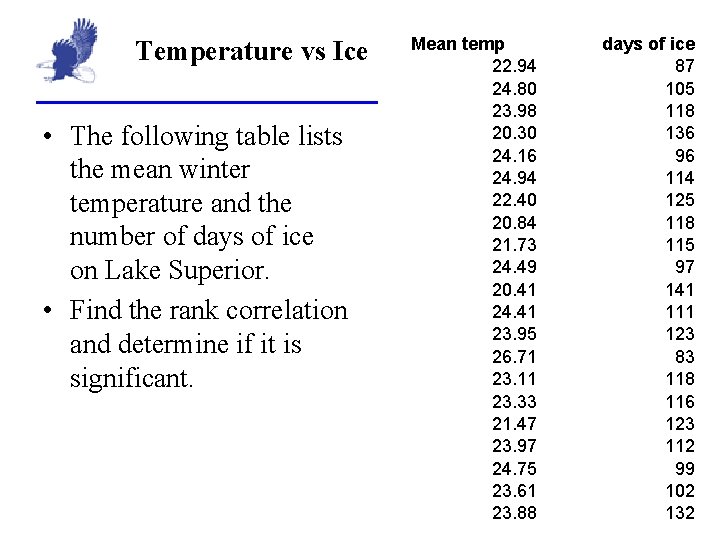
Temperature vs Ice • The following table lists the mean winter temperature and the number of days of ice on Lake Superior. • Find the rank correlation and determine if it is significant. Mean temp 22. 94 24. 80 23. 98 20. 30 24. 16 24. 94 22. 40 20. 84 21. 73 24. 49 20. 41 24. 41 23. 95 26. 71 23. 11 23. 33 21. 47 23. 97 24. 75 23. 61 23. 88 days of ice 87 105 118 136 96 114 125 118 115 97 141 111 123 83 118 116 123 112 99 102 132

Girls’ Bowling 120 Average 100 Average 80 60 40 20 0 0 1 2 3 Strikes 4 5 6

Problem Girls Bowling 1. r = 0. 905; positive/strong. As the girls’ strikes increase, their averages increase. 2. Critical value for a 95% degree of confidence is 0. 811. As r is beyond the critical value we reject the hypothesis that r is insignificant. 3. 4. The correlation is significant, use the function

Boys’ Bowling 130 Boys Bowling 120 110 100 Avera. GE 90 80 70 60 0 1 2 3 4 Strikes 5 6 7 8

Problem Boys Bowling 1. r = 0. 488; positive/weak. As the boy’s strikes increase, so does the average, but not consistently 2. Critical value for a 95% degree of confidence is 0. 707. As r is within the critical value we accept the hypothesis that r is insignificant. 3. 4. Since the correlation is not significant, we use the mean value for the estimate: 106. 5

GPA and SAT 800 700 600 SAT score 500 400 300 200 100 0 0 1 2 3 GPA 4 5 6

Problem GPA and SAT 1. r = 0. 859; positive perfect. As GPA increases, so does SAT score 2. Critical value is 0. 602. As r is beyond the critical value we reject the hypothesis that correlation is insignificant. 3. 4. The correlation is significant, use the function

Points and Wins 14 12 10 Wins 8 6 4 2 0 -200 -150 -100 -50 0 Points Difference 50 100 150

Points and wins 1. r = 0. 965; Positive strong. As the points difference increases, so do the points. 2. Critical value is 0. 632. As r is beyond the critical value, we reject the claim that the correlation is insignificant 3. 4. The correlation is significant, so we can use the equation.

Rank Correlation • Favorite color rank correlation: – r = 0. 761 – Critical value is 0. 600. As r is beyond the critical value, the correlation is significant • Temperature and ice – r = -0. 661 – Critical value is 0. 371. As r is beyond the critical value, the correlation is significant