Concepts Linguistic Support for Generic Programming in C

Concepts: Linguistic Support for Generic Programming in C++ Jaakko Järvi Bjarne Stroustrup Andrew Lumsdaine Douglas Gregor Jeremy Siek Gabriel Dos Reis 1

Generic Programming o A methodology for the construction of generic software libraries. n n o Dual focus on abstraction and efficiency Example: The C++ Standard Template Library Core notion: Lifting an algorithm 1. 2. 3. Start with concrete algorithms: int gcd(int a, int b) {. . . } Remove unnecessary requirements: template<typename Integral> Integral gcd(Integral a, Integral b) {. . . } Repeat: lift Integral to Commutative. Ring 2

Generic Programming in C++ o C++ templates enable the application of GP n n n o Overloading permits natural abstractions Instantiation eliminates cost of abstractions Many successful, generic libraries in C++ Significant problems remain: n n Inability to directly express ideas of GP Generic libraries in C++ are fragile Can we design better support for Generic Programming in C++ without sacrificing the performance and flexibility of templates? 3

Concepts for C++: Goals o o Support for the core ideas of Generic Programming in C++ Modular type checking for C++ templates Performance equivalent to C++ templates Complete backward compatibility n o o Library evolution is particularly important Simplicity Implementability 4

Concepts Overview o Three major parts: n Concept definitions: Specify the behavior of classes of types via requirements. n Where clauses: Specify constraints on template parameters in terms of concepts. n Concept maps: Specify how types meet the requirements of a concept. 5

Constrained Templates o Place constraints on template parameters via a where clause n n Uses of the template must satisfy these constraints Definition of the template can assume only what the constraints imply template<typename T> where Less. Than. Comparable<T> const T& min(const T& x, const T& y) { return x < y? x : y; } 6

Concept Definitions o Concept definitions state requirements on type parameters. concept Less. Than. Comparable<typename T> { bool operator<(T, T); axiom Irreflexivity(T x) { !(x < x); } axiom Transitivity(T x, T y, T z) { if (x < y && y < z) x < z; } } 7

Concept Parameterization o Concepts can have any number of parameters: concept Equality. Comparable<typename T, typename U> { bool operator==(T, U); bool operator!=(T, U); } 8

Iterator Concepts o Iterators abstract the notion of a sequence of values. concept Input. Iterator<typename Iter> { Iter& operator++(Iter&); Iter operator++(Iter&, int); bool operator==(Iter, Iter); bool operator!=(Iter, Iter); ? ? ? operator*(Iter); }; 9 // // // pre-increment post-increment equality comparison inequality comparison dereference

Iterators & Associated Types o value_type is the type that the iterator points to concept Input. Iterator<typename Iter> { typename value_type; Iter& operator++(Iter&); Iter operator++(Iter&, int); bool operator==(Iter, Iter); bool operator!=(Iter, Iter); value_type operator*(Iter); }; 10 // // // pre-increment post-increment equality comparison inequality comparison dereference

Iterators & Nested Requirements o difference_type measures sequence length concept Input. Iterator<typename Iter> { typename value_type; typename difference_type; where Signed. Integral<difference_type>; Iter& operator++(Iter&); // pre-increment Iter operator++(Iter&, int); // post-increment bool operator==(Iter, Iter); // equality comparison bool operator!=(Iter, Iter); // inequality comparison value_type operator*(Iter); // dereference }; 11

Using Associated Types o Implementing the STL find with concepts: template<typename Iter, typename T> where Input. Iterator<Iter> && Equality. Comparable<Input. Iterator<Iter>: : value_type, T> Iter find(Iter first, Iter last, const T& value) { while (first != last && !(*first == value)) ++first; return first; } 12

Concept Maps o We want to call find with an array of integers: bool contains(int* array, int n, int value) { return find(array, array + n, value) != array + n; } o Concept maps satisfy concept constraints: concept_map Input. Iterator<int*> { typedef int value_type; typedef ptrdiff_t difference_type; } 13

Concept Maps o We want to call find with an array of integers: bool contains(int* array, int n, int value) { return find(array, array + n, value) != array + n; } o Concept maps satisfy concept constraints: template<typename T> concept_map Input. Iterator<T*> { typedef T value_type; typedef ptrdiff_t difference_type; } 14

Concept Refinement o A bidirectional iterator can move backward: o A random access iterator can jump around: concept Bidirectional. Iterator<typename Iter> Input Iterator : Input. Iterator<Iter> { Iter& operator--(Iter&); Bidirectional Iter operator--(Iter&, int); Iterator } concept Random. Access. Iterator<typename Iter> : Bidirectional. Iterator<Iter> Random Access { Iterator Iter operator+(Iter, difference_type); // … } 15

Concept-Based Overloading o Advance an iterator x by n steps: template<Input. Iterator Iter> void advance(Iter& x, Iter: : difference_type n) { while (n > 0) { ++x; - -n; } } // O(n) template<Random. Access. Iterator Iter> void advance(Iter& x, Iter: : difference_type n) { x = x + n; } // O(1) o Compiler selects best match: n n advance(i, n); // O(1) or O(n)? Overloaded calls in generic algorithms can cause instantiation-time ambiguities (PLDI ‘ 06) 16

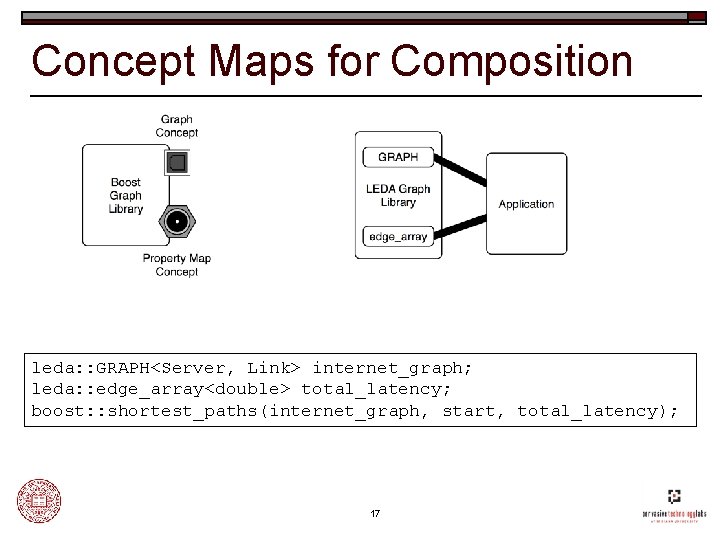
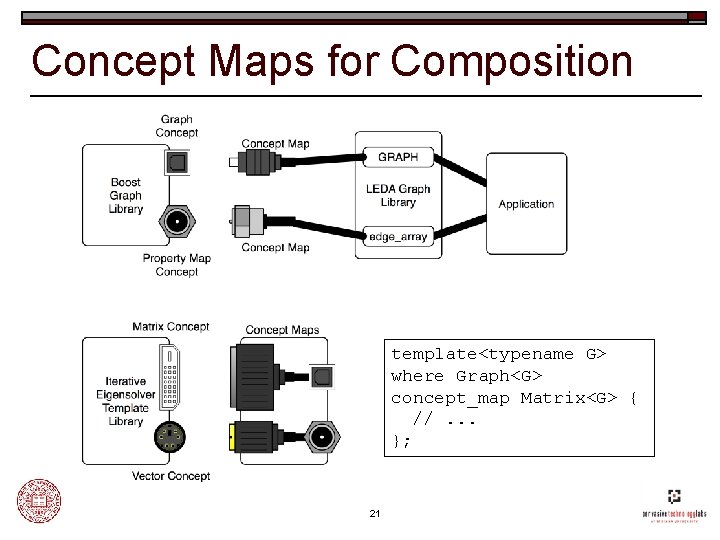
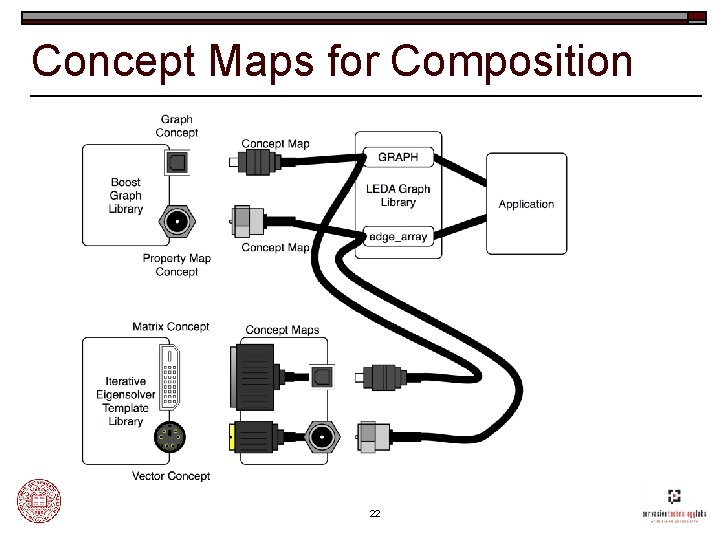
Concept Maps for Composition leda: : GRAPH<Server, Link> internet_graph; leda: : edge_array<double> total_latency; boost: : shortest_paths(internet_graph, start, total_latency); 17

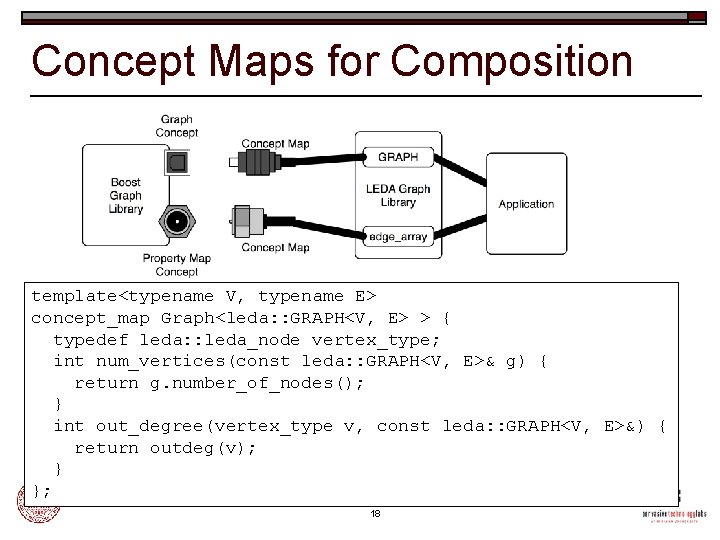
Concept Maps for Composition template<typename V, typename E> concept_map Graph<leda: : GRAPH<V, E> > { typedef leda: : leda_node vertex_type; int num_vertices(const leda: : GRAPH<V, E>& g) { return g. number_of_nodes(); } int out_degree(vertex_type v, const leda: : GRAPH<V, E>&) { return outdeg(v); } }; 18

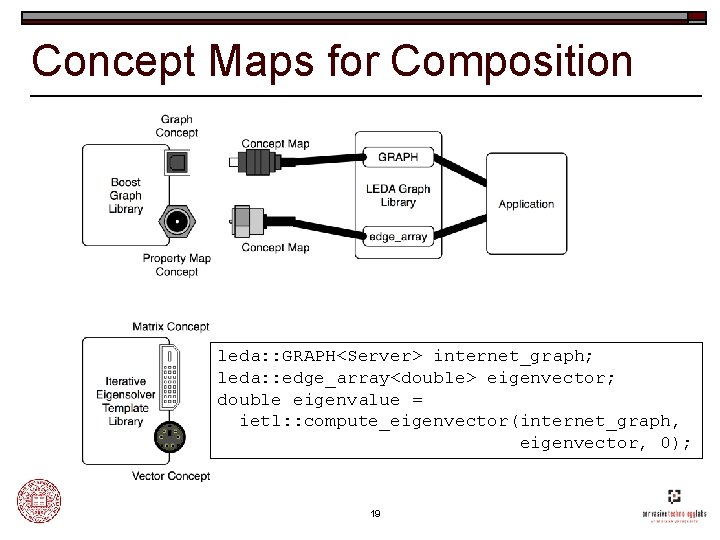
Concept Maps for Composition leda: : GRAPH<Server> internet_graph; leda: : edge_array<double> eigenvector; double eigenvalue = ietl: : compute_eigenvector(internet_graph, eigenvector, 0); 19

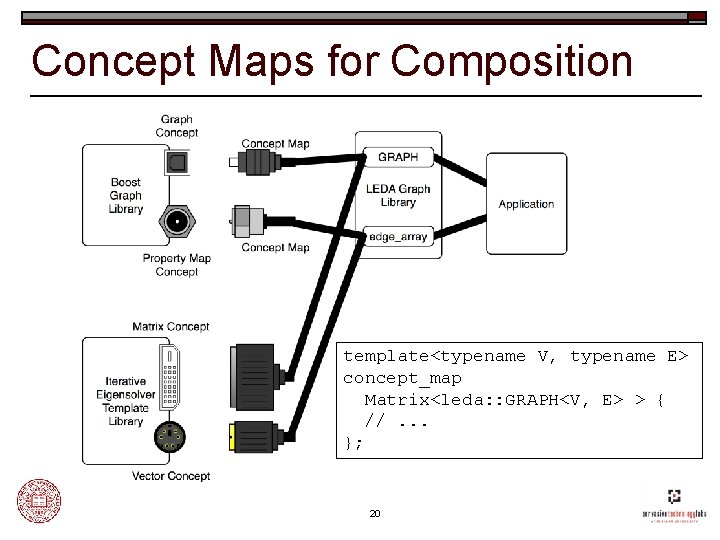
Concept Maps for Composition template<typename V, typename E> concept_map Matrix<leda: : GRAPH<V, E> > { //. . . }; 20

Concept Maps for Composition template<typename G> where Graph<G> concept_map Matrix<G> { //. . . }; 21

Concept Maps for Composition 22

Related Work o G o Haskell Type Classes o ML Signatures o Java, C# Generics o Fortress Traits 23

Summary: Concepts for C++ o Concepts provide complete support for Generic Programming in C++ n n o Transparent composition of generic libraries Seamless evolution of existing C++ code Prototype implementation in Concept. GCC Includes drop-in concept-enhanced STL http: //www. genericprogramming. org/software/Concept. GCC n o Strong candidate for inclusion in upcoming ISO C++ Standard, C++0 x 24