Concepts in Computer Science COP 2500 Spring 2006

Concepts in Computer Science COP 2500, Spring 2006 http: //www. cs. ucf. edu/courses/cop 2500 Keith Garfield garfield@cs. ucf. edu

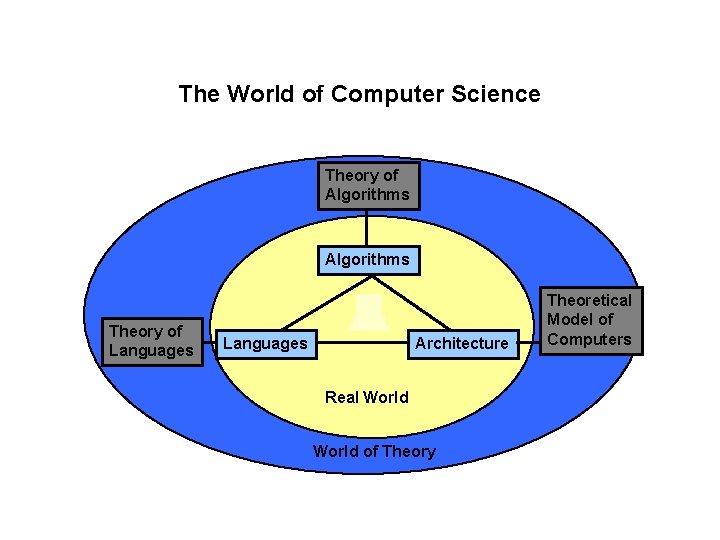
The World of Computer Science Theory of Algorithms Theory of Languages Architecture Real World of Theory Theoretical Model of Computers

What is Computer Science all About? What problems can a computer solve? What is the computational cost of the solution? • The answer to the first question tells us whether a problem should even be attempted using a computer. – Some problems are perfectly suited for computers, others are not. • The answer to the second question tells us if it is worth doing. – The cost is in terms of some resource like time or memory usage. – We attempt to relate cost to problem size. – Problems are grouped into classes depending on their cost (Chptr 11)

Purpose of the Course • Computer Capabilities: Inherent capabilities of any autonomous computing machine. • Basic CS concepts: Allows you to communicate with and work with CS people, and validate (or disprove), their ideas. • Programming? : Not trying to teach you to be programmers, but will require some programming to develop topics. • Program design: How does one go about planning a computer program? • Program implementation: How does my design get turned into working code?

Course Outline • Throughout the course we will use searching and sorting problems to illustrate points. • Topics (roughly in the same order as they are introduced) – – – Binary math Basic computer architecture Our model of a computer Introduction to Algorithms and Functions (Chapter 2) The cost of computation (Chapter 9) Transforming algorithms into code (Chapter 3, supplemental text) Computer languages: data types and data structures. (Chapter 3) Computer languages: program control mechanisms (Chapter 4) Computer Languages: Types of languages (Chapter 7) More about functions: recursion, iteration, modularity. (Chapter 4) Complex Data Structures. (Chapter 3, 5) The hierarchy of problems (Chapter 11)

Some First Thoughts • Computers are amazingly stupid. They have no sense of self, situation, or history. • Computers will only do what you tell them, and you must give them their directions in minute detail. • Computers store information in very limited ways. • Because of the above, computers are very good at some types of tasks and very bad at others. – Good: Mindless repetition with accuracy. – Bad: Creativity, intuition, “common sense”, and sensing. • We will use the above to discuss what computers can and cannot do: Can it be computed?

CS Concepts: Computational Power • Computational power refers to the types of problems a computer can solve. – It has nothing to do with how fast a computer is nor how nice the graphics are. • It turns out very simple computers are just as powerful than very expensive ones (although slower). • So in terms of computational power, all computers are equal. – This allows generalized solutions - solve a problem for one and we solve it for all. • Since all computers are equal, we tend to focus on types of problems rather than types of computers. – Is the problem computable?

CS Concepts: Computable Problems • Since all computers are equal, we tend to focus on types of problems rather than types of computers, – Is the problem computable? If yes, we’ll find a fast computer. • We are implying some problems are not (currently) computable. – Weather prediction is the most well known example. – Route planning is another. – Natural Language Processing is another. • This class focuses on computable problems – Sorting and searching. • We will look at sorting and searching methods in order to discuss basic CS ideas, terminology, and good practices. – This corresponds to chapters 2, 3, 4, 5, and 6 of text.

CS Concepts: What is computable? We will identify a small set of problems that Are computable, and a small set that are not Computable during this class. New problems can be mapped (correlated, Compared, translated) to the known problems And then deemed computable or not.

Patterns of 2’s in Computing • Computers operate on a binary system • Binary systems allow only two values – Zero or One – “On” or “Off” – “True” or “False” • Early computers were composed of groups of mechanical switches, each of which was “On” or “Off” at any time. • Modern computers store “bits” of data. Each bit can have the value of Zero or One. – The word BIT is a shortening of BINARY DIGIT

Computers Store Everything in Binary Form • So computer memory is nothing more than long sequences of bits (0’s and 1’s). • The most common unit of computer memory you see is the BYTE, which is simply a group of 8 bits. – How much memory does your PC at home have? It is always given in bytes, not bits. The same is true of file sizes. • These bits must be interpreted in special ways to be meaningful to humans – All data is represented as lists of 0’s and 1’s – Different types of data require different methods of interpretation to be meaningful. Numbers are different than letters, for example. – We will talk much more about data types throughout the semester.

Comparing Human and Computer Formats • • The human digits: Computer digits: • • Some human numbers: Computer numbers: • • The human alphabet: Aa, Bb, Cc, Dd, Ee, …. . Xx, Yy, Zz Computer alphabet: 0, 1 • • Some human words: “dog” “cat” Computer words: 0110010001101111101100111 011000110110001110100 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1 17 10001 42 31 101010 11111

Lets Look at Regular Math Again • Consider two math operations: taking a number to a power, and taking the log of a number. • We will focus on the number 2 (binary – no surprise) n 2 n n log 2 n 0 1 2 3 … 8 9 10 1 2 4 8 … 256 512 1024 0 1 2 3 … 8 9 10

How Much Information can we Store? • The number of bits assigned to a piece of information tells us how well we can describe the information. • The most abstract case: n bits allows 2 n distinct values. Bits Values Number Of Values 1 0 1 2 2 00 01 10 11 Bits 3 4 Values 000 001 010 011 100 101 110 111 Number Of Values 8

Example 1: Color Depth • How many colors are available if each pixel uses n bits? Bits Values Colors 1 0 1 Black White 00 01 10 11 Black Dark Gray Light Gray White 2 • Bits 3 Values Colors 000 001 010 011 100 101 110 111 Black Blue Green Yellow Red Purple Orange White How many bits are required for 256 colors? – 8 bits, because log 2 256 = 8 – That’s one byte – coincidence? ? ?

Example 2: Red-Green-Blue Format • One way to designate colors is setting values for the amount of red, green, and blue present in the mix. • The “digits” allowed in this system are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. • Each color component can have a value from 00 to FF – Examples of RGB colors might be FF 00 FF (fuschia), C 0 C 0 (silver) • How many bits are need to store the value of the color?

Example 2: Red-Green-Blue Format (cont) • How many bits are need to store the value of the color? How many bits are required for each “digit”? There are 16 distinct digits, and log 16 = 4 Each color component has two digits, so… Each color component requires 8 bits (or one byte – coincidence? A color is made up of three color components, so… 8 x 3 = 24 bits to specify a color. • How many distinct colors can be specified? 24 bits are used to specify the color, so… 224 = 16, 777, 216 (but in practice this is not done)

Example 3: Computer Memory • How much memory is on your computer? Is it a power of 2? • Lets assume a machine having 64 MB of RAM How many bits are required to specify a distinct memory location? Lets try 25 bits 225 = 33, 554, 432 (not enough) Lets try 26 bits 226 = 67, 108, 864 distinct values. 26 bits are required to specify a memory location. • How about 128 MB of RAM? 27 bits 227 = 134, 217, 728 27 bits are now required to specify a memory location. (twice the memory for one more bit – coincidence? )

Example 4: Computer Memory • What if we needed to assign a unique binary number to each of you in this class? How many bits would we need for each number? There about 90 of you. 1 bit 21 = 2 numbers. 2 bits 22 = 4 numbers. 3 bits 23 = 8 numbers. 4 bits 24 = 16 numbers. 5 bits 25 = 32 numbers. 6 bits 26 = 64 numbers. 7 bits 27 = 128 numbers. (This is more than the 90 required). Answer: 7 bits. This allows 90 unique values. • How many bits do we need to add if we double the class size?

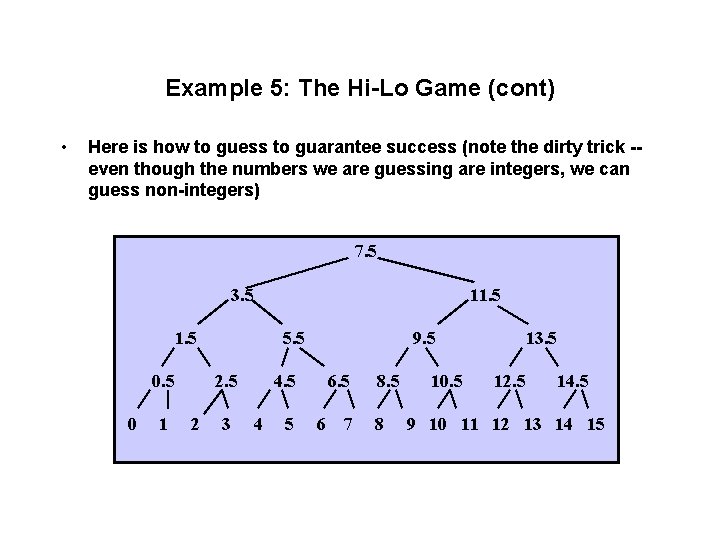
Example 5: The Hi-Lo Game • • I will give you five chances to guess an integer. Whenever you guess wrongly I will tell you whether the answer is higher or lower than your guess. Under what circumstances are you guaranteed success (the range of numbers can be considered the “size” of the problem)? – – – The numbers range from 0 – 3 The numbers range from 0 – 7 The numbers range from 0 – 15 The numbers range from 0 – 31 The numbers range from 0 – 63 We want the fifth guess to be perfect, so we only have fours guesses to play with. Each guess can correspond to a bit of information. 24 = 16 so I can discern 16 distinct values with my guesses. Answer: 0 – 15.

Example 5: The Hi-Lo Game (cont) • Here is how to guess to guarantee success (note the dirty trick -even though the numbers we are guessing are integers, we can guess non-integers) 7. 5 3. 5 11. 5 0 1 5. 5 2 3 9. 5 4 5 6 7 8. 5 8 10. 5 13. 5 12. 5 14. 5 9 10 11 12 13 14 15

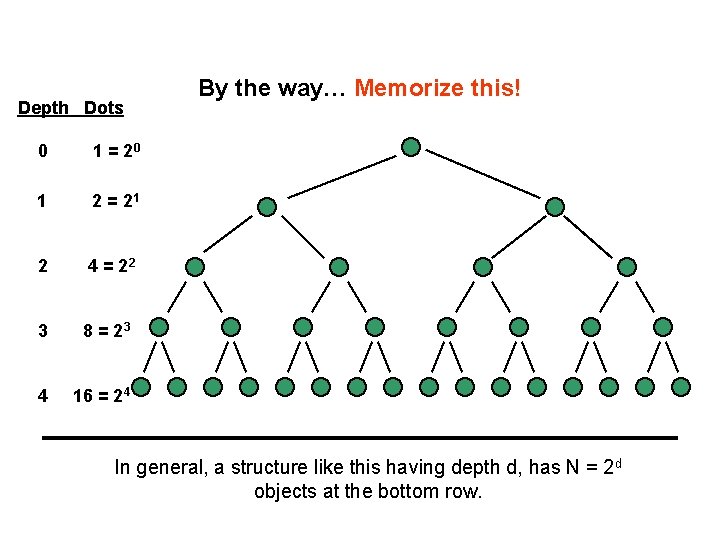
Depth Dots 0 1 = 20 1 2 = 21 2 4 = 22 3 8 = 23 4 16 = 24 By the way… Memorize this! In general, a structure like this having depth d, has N = 2 d objects at the bottom row.

Why do we Care? • We are trying to determine what kinds of problems are computable (ie capable of being solved by a computer). • These patterns we’ve seen will show up again and again: – Developing methods to solve problems and to determine the computational “cost” of the solution. – Determining what problem “sizes” are computable (example: hi-lo with 5 guesses and a range of 0 – 1000 is not computable. ) • Divide and Conquer (section 6. 4): – A basic and powerful method of solving problems. – We attempt to cut the size of the problem in half at each step. – This leads to a log n number of steps for problems of size n (and that’s good)

A Computer Model • Computer science is concerned with computation – What is computable? – How much effort is it to compute something? • We want the results to apply to all computers, not specific types or brands. • We need to develop an abstract model of a computer – Develop properties for theoretical computer. – Apply the properties to all real world computers.

Solution Space • Consider… – How many answers are there to 2 + 2 ? – How many answers are there to “Guess what color I am thinking of between red, green, and blue? ” – How many answers are there to “What’s your favorite color between red, green, and blue? ” – How many answers are their to “Is 3 > 2 ? ” – How many answers are their to “Guess which integer I am thinking of between 0 and 1. ” – How many answers are there to “Guess which number I am thinking of between 0 and 1. ”

Solution Space: The number of possible answers – right or wrong – to a question. • Solution space is sometimes called “search space” since often the answers must be searched through in some fashion. • Sometimes, solution space can give a clue as to the hardness of a problem – Large search spaces with no good mechanism (algorithm) for extracting the correct answer are intractable problems. – Small search spaces imply a problem can be solved even without an elegant solution.

A Computer Model • Computer science is concerned with computation – What is computable? – How much effort is it to compute something? • We want the results to apply to all computers, not specific types or brands. • We need to develop an abstract model of a computer – Develop properties for theoretical computer. – Apply the properties to all real world computers.

Computer Architecture (the Basics) • The following are components of a computer system from a commercial standpoint: – – – • The Central Processing Unit (CPU) Memory (Temporary data storage) Disk Space (permanent data storage) Monitor Keyboard Other input/output devices Do we need all of this for our abstract model?

Computer Architecture (the Basics) • Computer science is concerned with computation – What is computable? – How much effort is it to compute something? • Computer science focuses on the parts of the computer that deal with computation – Memory stores data and instructions – The CPU operates on the data per the instructions – Not input/output devices (monitors, keyboards, mice, etc) • We need a model for the CPU. • We need a model for memory

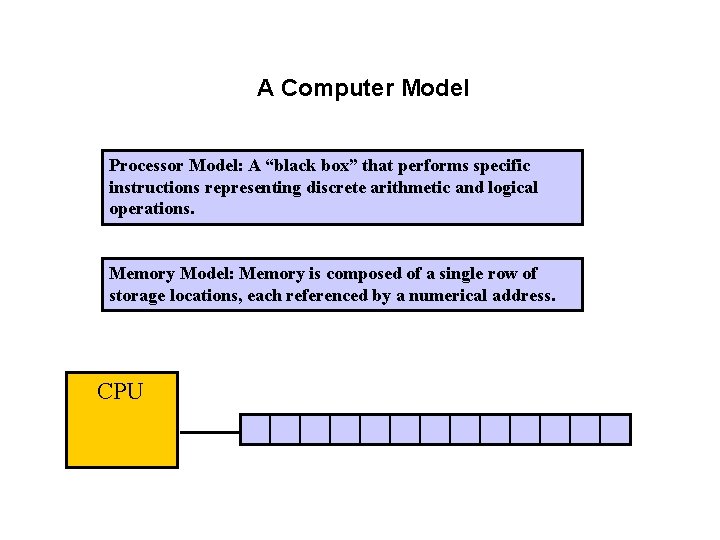
The CPU (Processor) Model • A real CPU has many elements, each devoted to specific types of operations (addition, multiplication, working with real numbers etc) • Our model of a Processor is much simpler: – A processor is a “black box” that can perform arithmetic and logical operations. – A processor performs one discrete operation at a time: • • Discrete: Add two numbers Discrete: Compare two numbers to see which is larger Discrete: Fetch a value from memory Not Discrete: Find the average of 20 numbers (too many operations) Processor Model: A “black box” that performs specific instructions representing discrete arithmetic and logical operations.

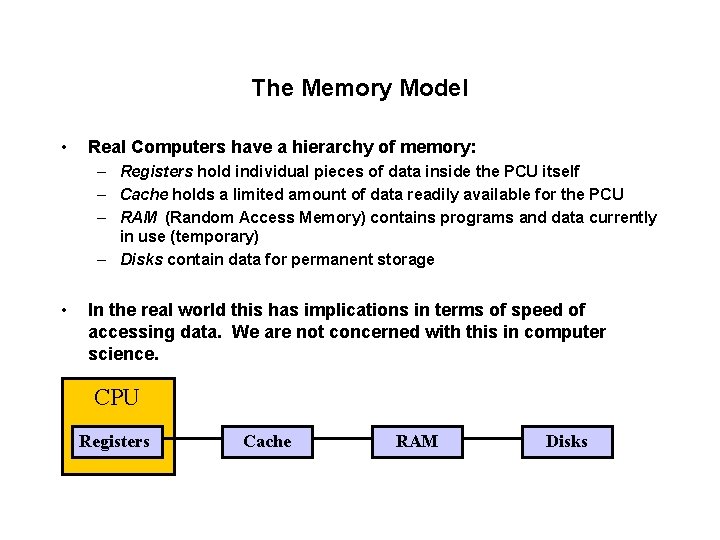
The Memory Model • Real Computers have a hierarchy of memory: – Registers hold individual pieces of data inside the PCU itself – Cache holds a limited amount of data readily available for the PCU – RAM (Random Access Memory) contains programs and data currently in use (temporary) – Disks contain data for permanent storage • In the real world this has implications in terms of speed of accessing data. We are not concerned with this in computer science. CPU Registers Cache RAM Disks

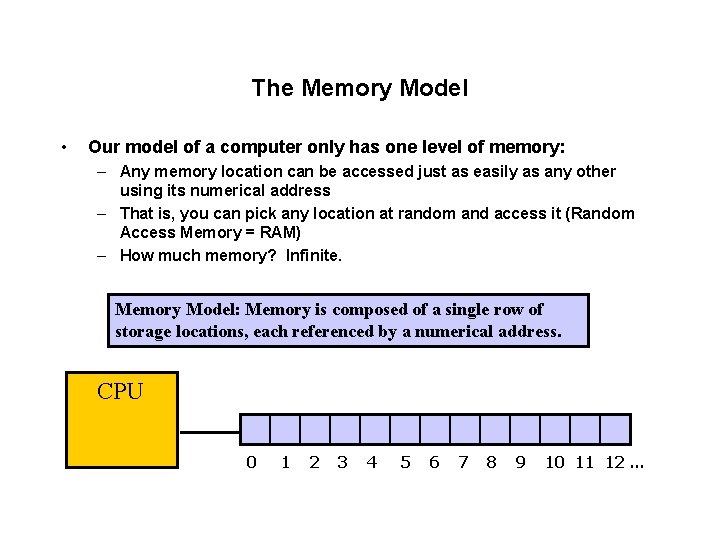
The Memory Model • Our model of a computer only has one level of memory: – Any memory location can be accessed just as easily as any other using its numerical address – That is, you can pick any location at random and access it (Random Access Memory = RAM) – How much memory? Infinite. Memory Model: Memory is composed of a single row of storage locations, each referenced by a numerical address. CPU 0 1 2 3 4 5 6 7 8 9 10 11 12 …

A Computer Model Processor Model: A “black box” that performs specific instructions representing discrete arithmetic and logical operations. Memory Model: Memory is composed of a single row of storage locations, each referenced by a numerical address. CPU

Summary of Theoretical Computer Model • This course is investigating what computers can and cannot do. • We want the results of this course to apply to all computers, not specific types or brands. • Therefore we use an abstract computer model that has the following characteristics: – Processor: A “black box” that performs specific instructions representing discrete arithmetic and logical operations. – Memory: An infinite number of boxes or pigeonholes, each referred to by a numeric address. • Now we can talk about what this thing can do.

Introduction to Variables • Remember that memory is a long series of boxes referred to by numerical addresses. • We could allow any numeric memory location to be used in our algorithms to store data in memory and then retrieving the data when we needed it. • The problem with using numeric memory addresses directly is twofold. – Programs with more than a few pieces of data would drive you crazy trying to keep track of where you put it. – Different real world machines have different memeory structures. 1 8 x y

Introduction to Variables • We use the concept of a variable to assign a name to the memory location. – Lets call our data "x" and "y". • We use a data declaration to tell the computer that we are using variable names to help us store data. – Declarations need to specify the variable NAME, TYPE, and STRUCTURE. • The computer will assign memory locations to each variable: – Here, “x” is associated with memory location 1. – Here, “y” is associated with memory location 8. 1 8 x y

Data Types and Data Structures • When specifying data in a program we need to describe its name, type and its structure. • Data's type impose meaning onto data (semantics) and data's structure impose organization (syntax) onto data. • Data Type (definition): A label applied to data that tells the computer how to interpret and manipulate data. – Type tells the computer how much space to reserve for variables and how to interpret operations on them. • Data Structure (definition): The way data is organized logically. – Describes how different pieces of data are organized.