Computing transit time components from a regional analysis

Computing transit time components from a regional analysis: A practical implementation 6 th European HICUM Workshop June 12, 13, 2006 - Heilbronn N. Kauffmann STMicroelectronics

Introduction q The regional approach • Bipolar transistor divided into neutral (WE , WB , WC) and SCR (WBE , WBC ) regions Detection of an hole injection layer (WI) in the collector • Decomposition based on DC and quasi-static analysis, in 1 D only • Transit time components computed from the above decomposition: TF = TE + TBC + TC q Importance of the regional approach • Educational purpose, better understanding of bipolar physics • Device optimization • First order model parameters extraction q Practical Test • Database of 1 D NPN Si. Ge simulations • DEVICE Simulator (Drift-Diffusion only) • Regional data computed and checked for all members of the database • Note : 1 D simulation only available so far (no 2 D/3 D effects) and S Node not Available N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 2

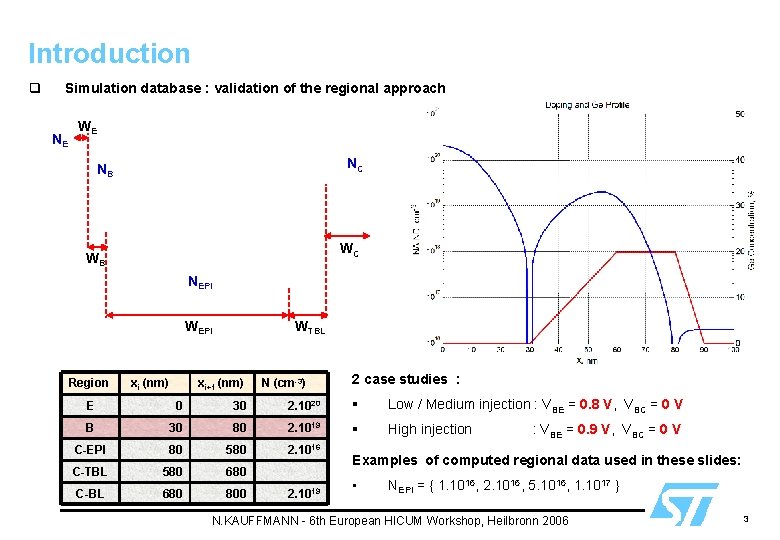
Introduction q Simulation database : validation of the regional approach NE WE NC NB WC WB NEPI WEPI Region xi (nm) WTBL xi+1 (nm) N (cm-3) 2 case studies : E 0 30 2. 1020 § Low / Medium injection : VBE = 0. 8 V, VBC = 0 V B 30 80 2. 1019 § High injection C-EPI 80 580 2. 1016 C-TBL 580 680 C-BL 680 800 2. 1019 : VBE = 0. 9 V, VBC = 0 V Examples of computed regional data used in these slides: • NEPI = { 1. 1016, 2. 1016, 5. 1016, 1. 1017 } N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 3

Outline Introduction Regional approach Examples Conclusion N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 4

Regional Approach - Definitions 1. Transit times • TF : Forward transit time (BC Short) • TR : Reverse transit time (BE Short) • TFF : Total transit time from CE Short, = 1 / (2 p FT) 2. Transit time components • TE : Transit time of minority carriers in the neutral emitter • TBE : Transit time of minority carriers in the BE SCR • TB : Transit time of minority carriers in the neutral base and BC SCR (electrons) • TC : Transit time of minority carriers in the neutral collector and BC SCR (holes) • TBC : Recharging time of the BC SCR (transport of majority carriers – electrons) 3. Charges • Qm : Minority charge Qm = { QN • QC : Uncompensated charge QC = if |QN| < |QP| , QP otherwise } Q P - QN N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 5

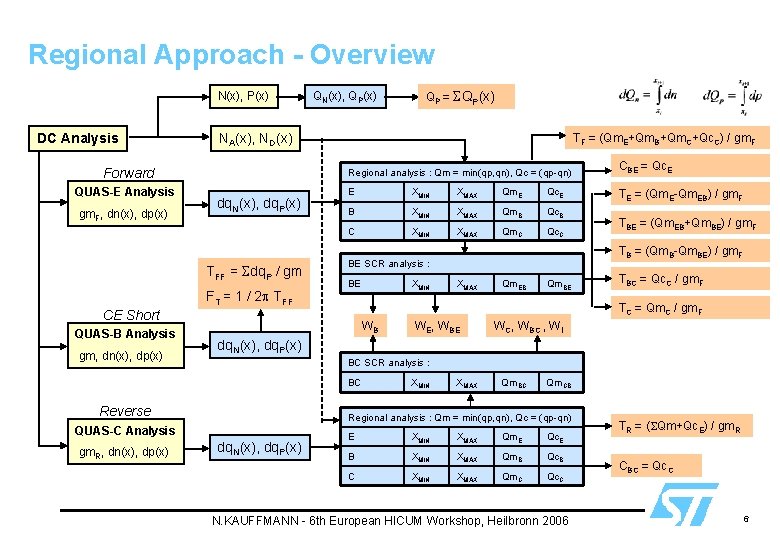
Regional Approach - Overview N(x), P(x) DC Analysis gm. F, dn(x), dp(x) TF = (Qm. E+Qm. B+Qm. C+Qc. C) / gm. F Regional analysis : Qm = min(qp, qn), Qc = (qp-qn) dq. N(x), dq. P(x) TFF = Sdq. P / gm FT = 1 / 2 p TFF E XMIN XMAX Qm. E Qc. E B XMIN XMAX Qm. B Qc. B C XMIN XMAX Qm. C Qc. C BE gm, dn(x), dp(x) TE = (Qm. E-Qm. EB) / gm. F TBE = (Qm. EB+Qm. BE) / gm. F XMAX Qm. EB Qm. BE TBC = Qc. C / gm. F TC = Qm. C / gm. F WB WE, WBE WC, WBC , WI dq. N(x), dq. P(x) BC SCR analysis : BC Reverse XMIN XMAX Qm. BC Qm. CB Regional analysis : Qm = min(qp, qn), Qc = (qp-qn) QUAS-C Analysis gm. R, dn(x), dp(x) XMIN CBE = Qc. E TB = (Qm. B-Qm. BE) / gm. F BE SCR analysis : CE Short QUAS-B Analysis QP = SQP(x) NA(x), ND(x) Forward QUAS-E Analysis QN(x), QP(x) dq. N(x), dq. P(x) E XMIN XMAX Qm. E Qc. E B XMIN XMAX Qm. B Qc. B C XMIN XMAX Qm. C Qc. C N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 TR = (SQm+Qc. E) / gm. R CBC = Qc. C 6

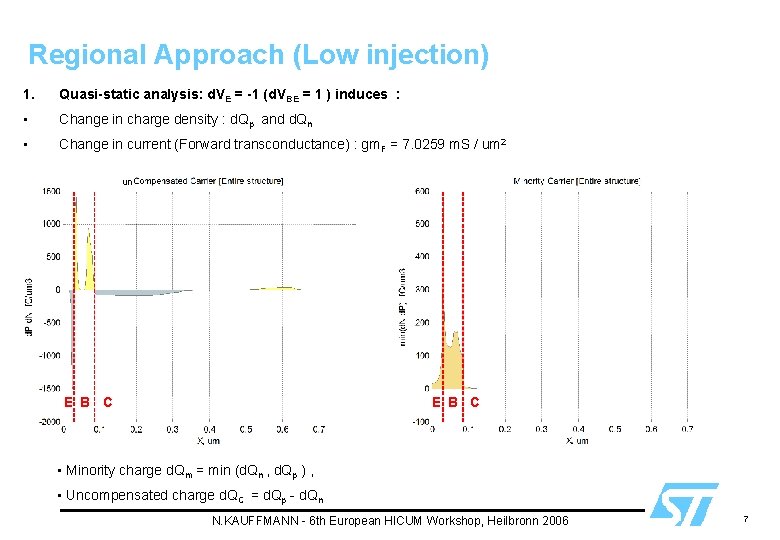
Regional Approach (Low injection) 1. Quasi-static analysis: d. VE = -1 (d. VBE = 1 ) induces : • Change in charge density : d. Qp and d. Qn • Change in current (Forward transconductance) : gm. F = 7. 0259 m. S / um 2 un E B C • Minority charge d. Qm = min (d. Qn , d. Qp ) , • Uncompensated charge d. QC = d. Qp - d. Qn N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 7

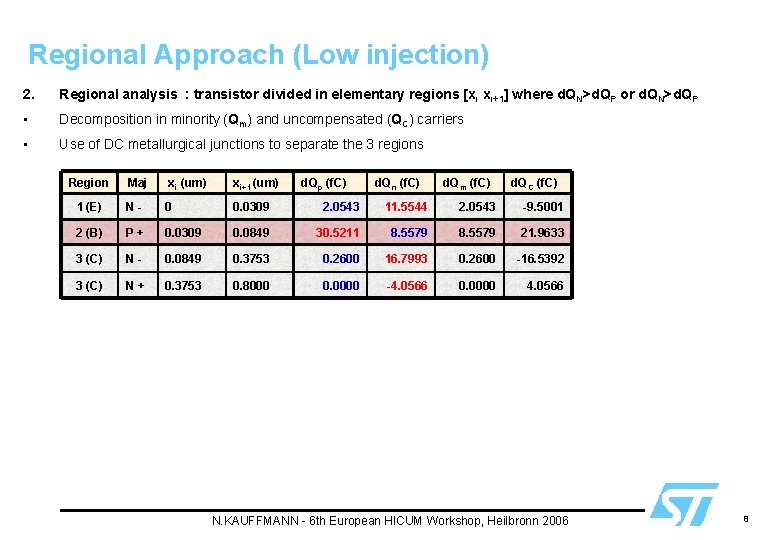
Regional Approach (Low injection) 2. Regional analysis : transistor divided in elementary regions [x i xi+1] where d. QN>d. QP or d. QN>d. QP • Decomposition in minority (Qm) and uncompensated (QC) carriers • Use of DC metallurgical junctions to separate the 3 regions Region Maj xi (um) xi+1 (um) d. Qp (f. C) d. Qn (f. C) d. Qm (f. C) d. QC (f. C) 1 (E) N- 0 0. 0309 2. 0543 11. 5544 2. 0543 -9. 5001 2 (B) P+ 0. 0309 0. 0849 30. 5211 8. 5579 21. 9633 3 (C) N- 0. 0849 0. 3753 0. 2600 16. 7993 0. 2600 -16. 5392 3 (C) N+ 0. 3753 0. 8000 0. 0000 -4. 0566 0. 0000 4. 0566 N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 8

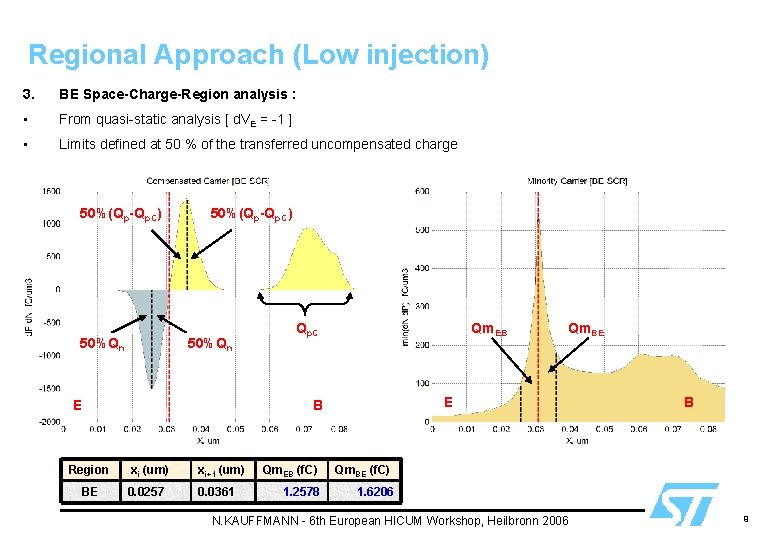
Regional Approach (Low injection) 3. BE Space-Charge-Region analysis : • From quasi-static analysis [ d. VE = -1 ] • Limits defined at 50 % of the transferred uncompensated charge 50%(Qp-Qp. C) 50%Qn E Qp. C Qm. EB E B Region BE xi (um) xi+1 (um) 0. 0257 0. 0361 Qm. EB (f. C) 1. 2578 Qm. BE B Qm. BE (f. C) 1. 6206 N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 9

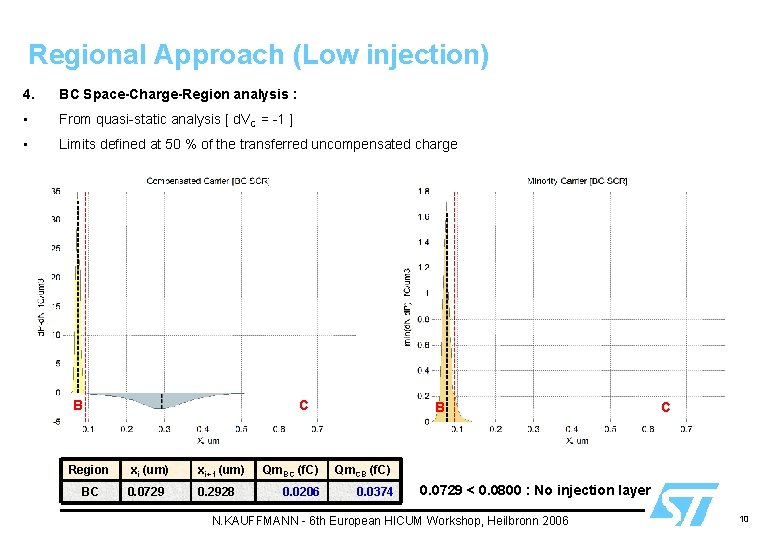
Regional Approach (Low injection) 4. BC Space-Charge-Region analysis : • From quasi-static analysis [ d. VC = -1 ] • Limits defined at 50 % of the transferred uncompensated charge B Region BC C xi (um) xi+1 (um) 0. 0729 0. 2928 B Qm. BC (f. C) Qm. CB (f. C) 0. 0206 0. 0374 C 0. 0729 < 0. 0800 : No injection layer N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 10

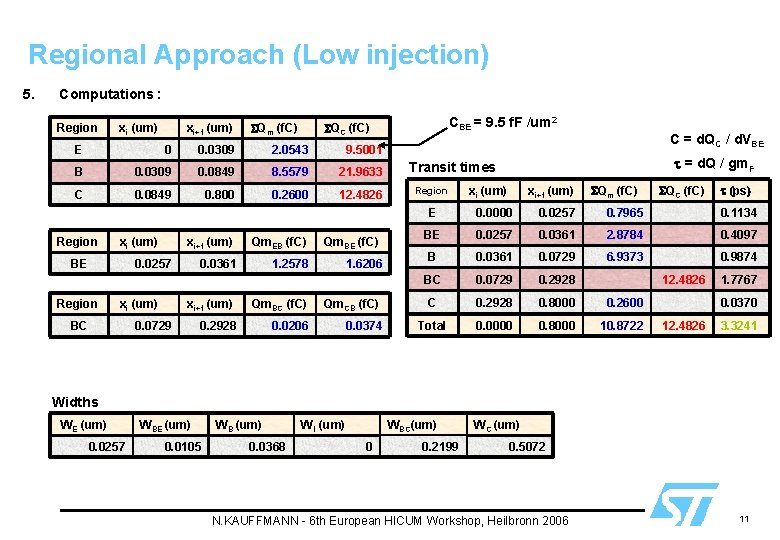
Regional Approach (Low injection) 5. Computations : Region xi (um) xi+1 (um) SQm (f. C) E 0 0. 0309 2. 0543 9. 5001 B 0. 0309 0. 0849 8. 5579 21. 9633 C 0. 0849 0. 800 0. 2600 12. 4826 Region xi (um) BE xi+1 (um) Qm. EB (f. C) 0. 0361 1. 2578 0. 0257 Region xi (um) BC Qm. BE (f. C) 1. 6206 xi+1 (um) Qm. BC (f. C) Qm. CB (f. C) 0. 2928 0. 0206 0. 0374 0. 0729 CBE = 9. 5 f. F /um 2 SQC (f. C) C = d. QC / d. VBE t = d. Q / gm. F Transit times Region xi (um) xi+1 (um) SQm (f. C) SQC (f. C) t (ps) E 0. 0000 0. 0257 0. 7965 0. 1134 BE 0. 0257 0. 0361 2. 8784 0. 4097 B 0. 0361 0. 0729 6. 9373 0. 9874 BC 0. 0729 0. 2928 C 0. 2928 0. 8000 0. 2600 Total 0. 0000 0. 8000 10. 8722 12. 4826 1. 7767 0. 0370 12. 4826 3. 3241 Widths WE (um) 0. 0257 WBE (um) 0. 0105 WB (um) 0. 0368 WI (um) WBC(um) 0 0. 2199 WC (um) 0. 5072 N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 11

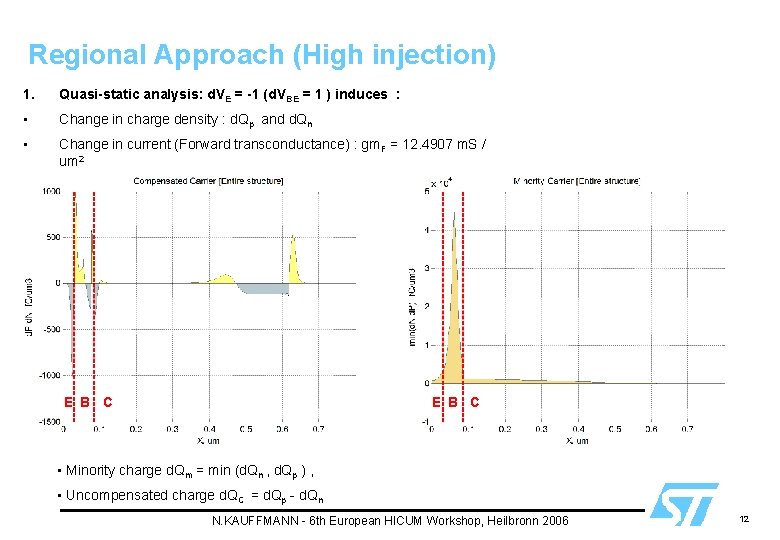
Regional Approach (High injection) 1. Quasi-static analysis: d. VE = -1 (d. VBE = 1 ) induces : • Change in charge density : d. Qp and d. Qn • Change in current (Forward transconductance) : gm. F = 12. 4907 m. S / um 2 E B C • Minority charge d. Qm = min (d. Qn , d. Qp ) , • Uncompensated charge d. QC = d. Qp - d. Qn N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 12

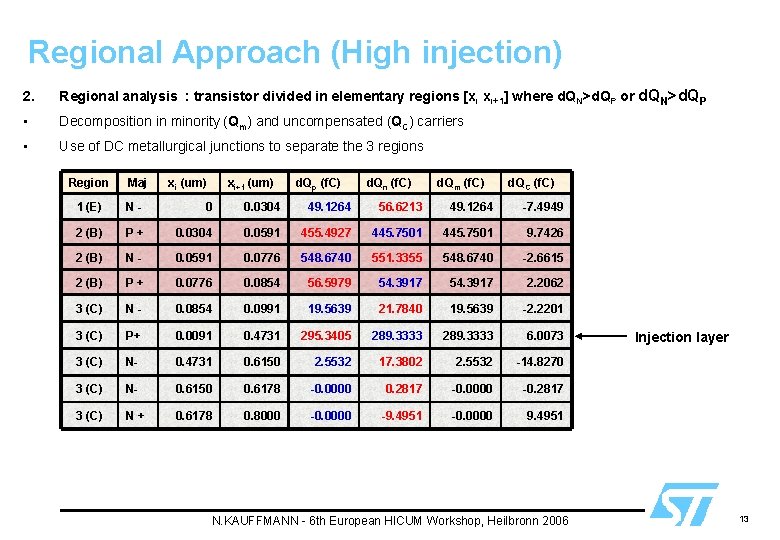
Regional Approach (High injection) 2. Regional analysis : transistor divided in elementary regions [x i xi+1] where d. QN>d. QP or d. QN>d. QP • Decomposition in minority (Qm) and uncompensated (QC) carriers • Use of DC metallurgical junctions to separate the 3 regions Region Maj xi (um) xi+1 (um) d. Qp (f. C) d. Qn (f. C) d. Qm (f. C) d. QC (f. C) 1 (E) N- 0 0. 0304 49. 1264 56. 6213 49. 1264 -7. 4949 2 (B) P+ 0. 0304 0. 0591 455. 4927 445. 7501 9. 7426 2 (B) N- 0. 0591 0. 0776 548. 6740 551. 3355 548. 6740 -2. 6615 2 (B) P+ 0. 0776 0. 0854 56. 5979 54. 3917 2. 2062 3 (C) N- 0. 0854 0. 0991 19. 5639 21. 7840 19. 5639 -2. 2201 3 (C) P+ 0. 0091 0. 4731 295. 3405 289. 3333 6. 0073 3 (C) N- 0. 4731 0. 6150 2. 5532 17. 3802 2. 5532 -14. 8270 3 (C) N- 0. 6150 0. 6178 -0. 0000 0. 2817 -0. 0000 -0. 2817 3 (C) N+ 0. 6178 0. 8000 -0. 0000 -9. 4951 -0. 0000 9. 4951 N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 Injection layer 13

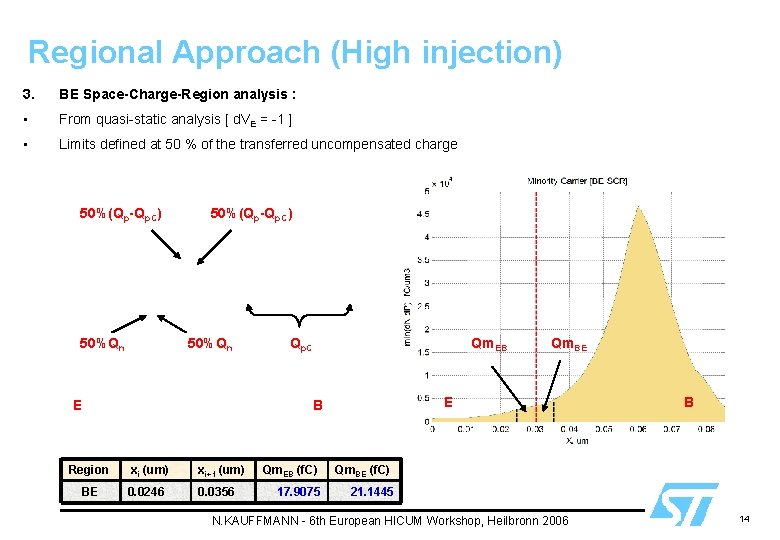
Regional Approach (High injection) 3. BE Space-Charge-Region analysis : • From quasi-static analysis [ d. VE = -1 ] • Limits defined at 50 % of the transferred uncompensated charge 50%(Qp-Qp. C) 50%Qn E Qp. C Qm. EB E B Region BE xi (um) xi+1 (um) 0. 0246 0. 0356 Qm. EB (f. C) 17. 9075 Qm. BE B Qm. BE (f. C) 21. 1445 N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 14

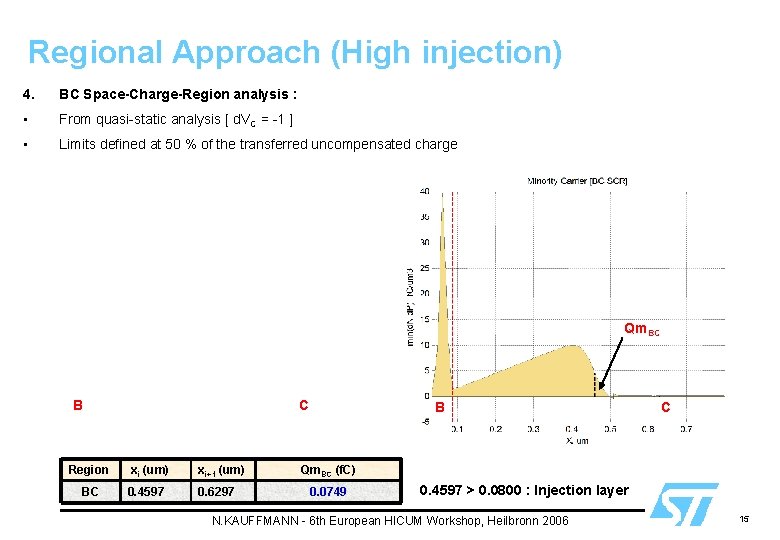
Regional Approach (High injection) 4. BC Space-Charge-Region analysis : • From quasi-static analysis [ d. VC = -1 ] • Limits defined at 50 % of the transferred uncompensated charge Qm. BC B Region BC C xi (um) xi+1 (um) 0. 4597 0. 6297 B C Qm. BC (f. C) 0. 0749 0. 4597 > 0. 0800 : Injection layer N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 15

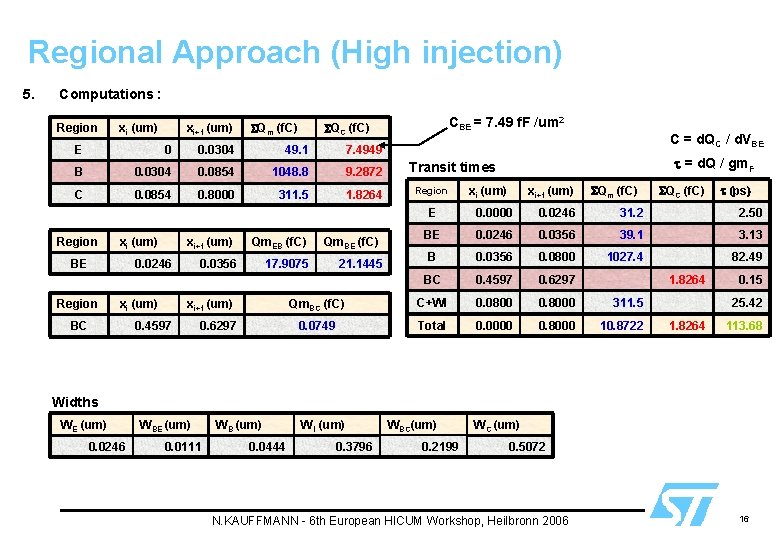
Regional Approach (High injection) 5. Computations : Region xi (um) xi+1 (um) SQm (f. C) E 0 0. 0304 49. 1 7. 4949 B 0. 0304 0. 0854 1048. 8 9. 2872 C 0. 0854 0. 8000 311. 5 1. 8264 Region xi (um) BE Region xi (um) BC xi (um) xi+1 (um) SQm (f. C) SQC (f. C) t (ps) 31. 2 2. 50 BE 0. 0246 0. 0356 39. 1 3. 13 B 0. 0356 0. 0800 1027. 4 82. 49 BC 0. 4597 0. 6297 Qm. BC (f. C) C+WI 0. 0800 0. 8000 311. 5 0. 0749 Total 0. 0000 0. 8000 10. 8722 17. 9075 0. 6297 Region 0. 0246 0. 0356 0. 4597 t = d. Q / gm. F Transit times 0. 0000 Qm. EB (f. C) xi+1 (um) C = d. QC / d. VBE E xi+1 (um) 0. 0246 CBE = 7. 49 f. F /um 2 SQC (f. C) Qm. BE (f. C) 21. 1445 1. 8264 0. 15 25. 42 1. 8264 113. 68 Widths WE (um) 0. 0246 WBE (um) 0. 0111 WB (um) 0. 0444 WI (um) 0. 3796 WBC(um) 0. 2199 WC (um) 0. 5072 N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 16

Outline Introduction Regional approach Examples Conclusion N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 17

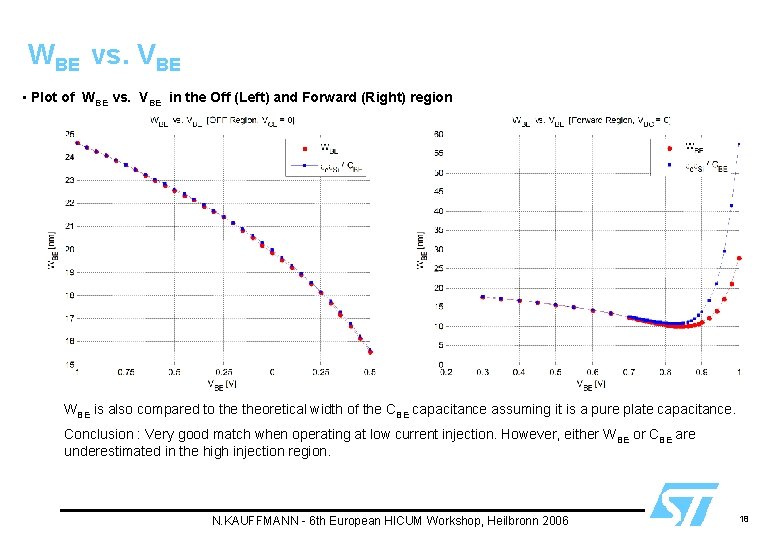
WBE vs. VBE • Plot of WBE vs. VBE in the Off (Left) and Forward (Right) region WBE is also compared to theoretical width of the CBE capacitance assuming it is a pure plate capacitance. Conclusion : Very good match when operating at low current injection. However, either WBE or CBE are underestimated in the high injection region. N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 18

WBC vs. IC @ VBC = -2 V • Plot of WBC vs. IC for NEPI = { 1. 1016, 2. 1016, 5. 1016, 1. 1017 } 0. 28 um um 0. 43 umum 0. 54 The simulated DC electric field of the current operating point (red dot) is plotted in the right figure, allowing a crude evaluation of the BC SCR width. WBC appears to be very close to the width of the BC SCR defined by the electric field. The maximum value of WBC is 0. 55 mm, close from theory (WBC≈ WEPI) Note that when the doping concentration of the epitaxy layer is very low, WBC does not enter the buried layer and its value is therefore shorter than what is estimated by the electric field. N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 19

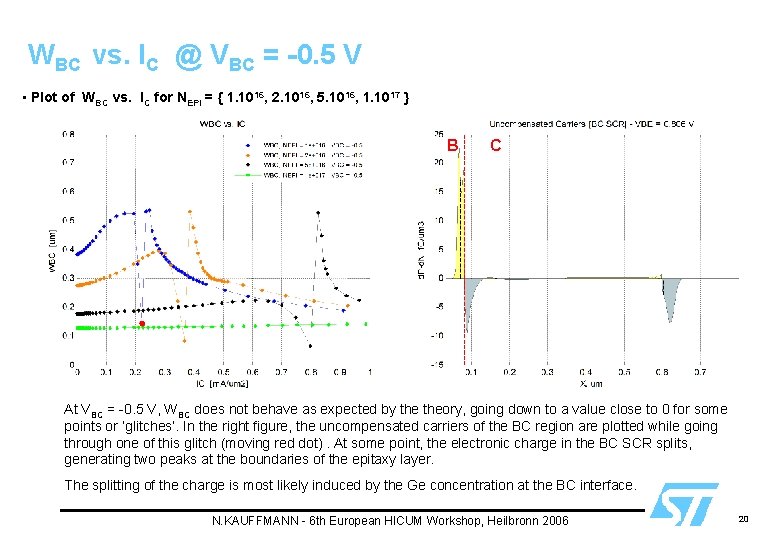
WBC vs. IC @ VBC = -0. 5 V • Plot of WBC vs. IC for NEPI = { 1. 1016, 2. 1016, 5. 1016, 1. 1017 } B C At VBC = -0. 5 V, WBC does not behave as expected by theory, going down to a value close to 0 for some points or ‘glitches’. In the right figure, the uncompensated carriers of the BC region are plotted while going through one of this glitch (moving red dot). At some point, the electronic charge in the BC SCR splits, generating two peaks at the boundaries of the epitaxy layer. The splitting of the charge is most likely induced by the Ge concentration at the BC interface. N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 20

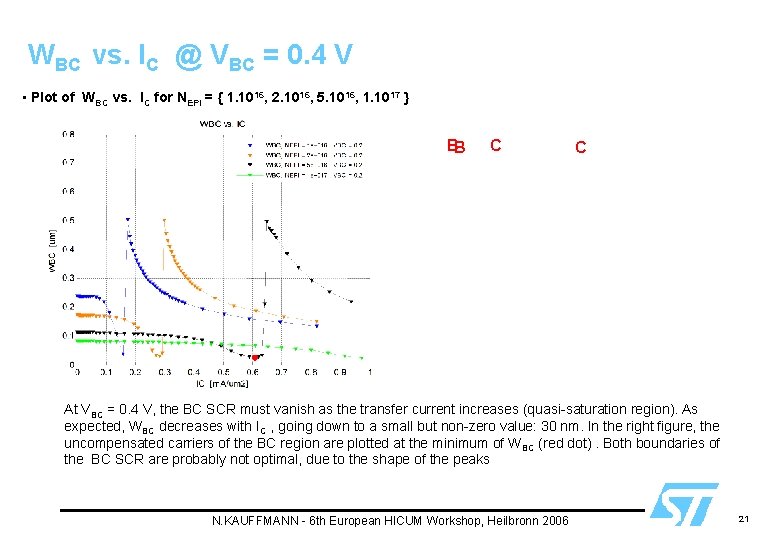
WBC vs. IC @ VBC = 0. 4 V • Plot of WBC vs. IC for NEPI = { 1. 1016, 2. 1016, 5. 1016, 1. 1017 } BB C C At VBC = 0. 4 V, the BC SCR must vanish as the transfer current increases (quasi-saturation region). As expected, WBC decreases with IC , going down to a small but non-zero value: 30 nm. In the right figure, the uncompensated carriers of the BC region are plotted at the minimum of WBC (red dot). Both boundaries of the BC SCR are probably not optimal, due to the shape of the peaks N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 21

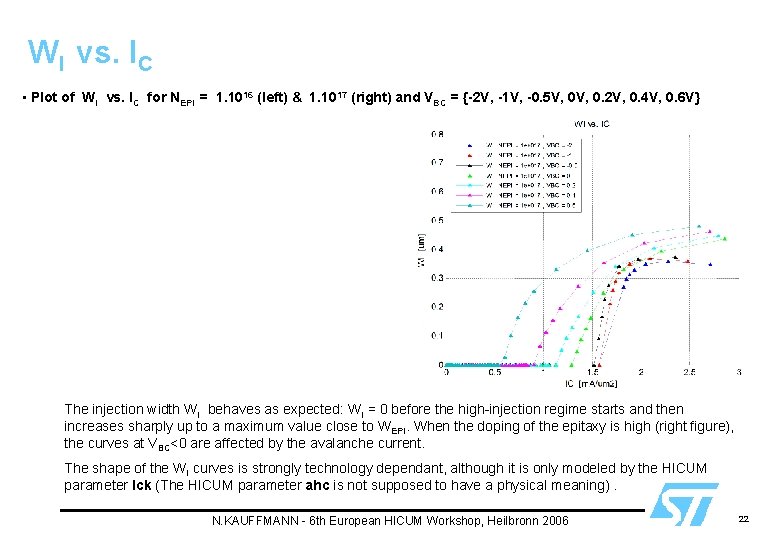
WI vs. IC • Plot of WI vs. IC for NEPI = 1. 1016 (left) & 1. 1017 (right) and VBC = {-2 V, -1 V, -0. 5 V, 0. 2 V, 0. 4 V, 0. 6 V} The injection width WI behaves as expected: WI = 0 before the high-injection regime starts and then increases sharply up to a maximum value close to WEPI. When the doping of the epitaxy is high (right figure), the curves at VBC<0 are affected by the avalanche current. The shape of the WI curves is strongly technology dependant, although it is only modeled by the HICUM parameter Ick (The HICUM parameter ahc is not supposed to have a physical meaning). N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 22

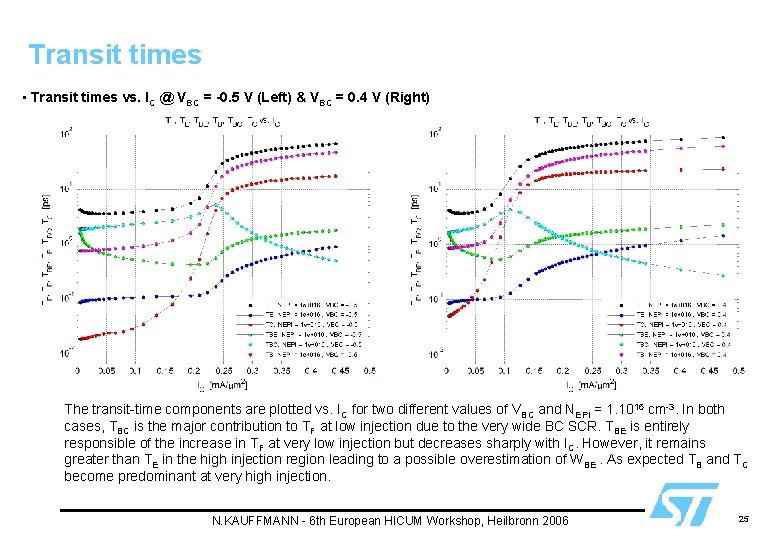
Transit times • Transit times vs. IC @ VBC = -0. 5 V (Left) & VBC = 0. 4 V (Right) The transit-time components are plotted vs. IC for two different values of VBC and NEPI = 1. 1016 cm-3. In both cases, TBC is the major contribution to TF at low injection due to the very wide BC SCR. TBE is entirely responsible of the increase in TF at very low injection but decreases sharply with IC. However, it remains greater than TE in the high injection region leading to a possible overestimation of WBE. As expected TB and TC become predominant at very high injection. N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 25

Outline Introduction Regional approach Examples Conclusion N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 27

Conclusion 1. Regional Approach implementation • Bipolar transistor structure divided in neutral and SCR regions using DC & quasi-static information • Region assignment based on quasi-static data and DC metallurgical boundaries • Definition of SCR Boundaries : 50% of the SCR quasi-static electron / hole charge displaced • So far, no transit time component for BC SCR minority carriers – majority carriers only 2. Test & qualitative results • Database of 1 D TCAD simulations of NPN-Si. Ge transistors – DEVICE Simulator used (Drift/diffusion) • Very smooth and robust results over the entire database • Results physically consistent : Transit times, region widths behave as expected 3. Quantitative results • Quasi-static charge distribution probably affected by Ge content leading to more complex peak structures • Results are usually very good but in some cases, they may not be fully optimal. • AC simulations required to validate the variations of the BE and BC capacitances with I C 4. Perspectives • Extraction of a first order set of HICUM parameters • 2 D extension, S node N. KAUFFMANN - 6 th European HICUM Workshop, Heilbronn 2006 28