Computing the Density of States of Boolean Formulas

Computing the Density of States of Boolean Formulas Stefano Ermon, Carla Gomes, and Bart Selman Cornell University, September 2010

Motivation: Significant progress in SAT From 100 variables, 200 constraints (early 90’s) to over 1, 000 vars. and 5, 000 clauses in 20 years. Applications: Hardware and Software Verification, Planning, Scheduling, Optimal Control, Protocol Design, Routing, Multi-agent systems, E-Commerce (E-auctions and electronic trading agents), etc. SAT: Given a Boolean formula Φ in CNF, Φ=C 1ΛC 2 Λ…ΛCm does Φ have a satisfying assignment?

Extending SAT technology n Model counting problem (number of distinct satisfying assignments): probabilistic inference problems n multi-agent / adversarial reasoning (bounded) [Roth ‘ 96, Littman et. al. ‘ 01, Sang et. al. ‘ 04, Darwiche ‘ 05, Domingos ‘ 06] n n MAX-SAT and Weighted MAX-SAT: find a truth assignment that maximizes the number of satisfied clauses or the sum of their weights n n beyond decision (NP) [Hansen at al. ’ 90] hard and soft constraints [Heras et al. ’ 08, Cohen et al. ’ 06] How can we combine both challenges?

Density of states n Given a Boolean formula Φ in CNF, Φ=C 1ΛC 2 Λ…ΛCm with m clauses the density of states is a function that gives the number of truth assignments that violate exactly i clauses, for i =0, . . , m n n n(0) = number of assignments that violate 0 clauses (models) n(1) = number of assignments that violate exactly 1 clause

Density of states: a challenging problem n Generalizes SAT ¨ n Generalizes MAX-SAT ¨ n Decision problem: Φ is satisfiable if and only if n(0)>0 MAX-SAT is the minimum i such that n(i)>0 Generalizes #SAT ¨ Number of models = n(0)

Statistical physics n More generally, the density of states (DOS) gives the number of microstates with energy E ¨ Microstates = truth assignments ¨ Energy = number of violated clauses ¨ Ground states = maximally satisfying assignments n Compact, very informative characterization of a physical system ¨ Macroscopic thermodynamic quantities (free energy, internal energy, . . ) ¨ Partition function, phase transitions, . .

Motivation n n DOS provides a finer characterization of the structure of a combinatorial search space Statistical physics and CSPs: ¨ Insights on problem structure, hardness, new algorithms, Survey Propagation [Montanari et. al. ‘ 07, Monasson et. al. ‘ 96, Mézard ’ 02, Parisi ‘ 02] n By defining different energy functions, it can be naturally used for probabilistic style inference (e. g. Markov Logic, [Domingos ‘ 06] )

Talk Outline n n n Prior work A novel sampling strategy: MCMC-Flat. Sat Empirical Validation ¨ Small formulas with ground truth ¨ Synthetic formulas ¨ Random 3 -SAT ¨ Large structured instances ¨ Model counting n Conclusions

Density of states: prior work n n Exact Method: Enumeration (exponential) Approximate ¨ Uniform n n Sampling [Belaidouni et. al. ‘ 02] Sample density from K random truth assignments Impractical, unlikely to hit rare assignments (e. g. solutions) ¨ Metropolis n n Sampling [Rose et. al. ‘ 96] In theory, the density can be extracted from the Boltzmann distribution Impractical, difficult choice of the temperature and slow mixing times [Wei et. al. ‘ 04 ] How can we improve the sampling strategy?

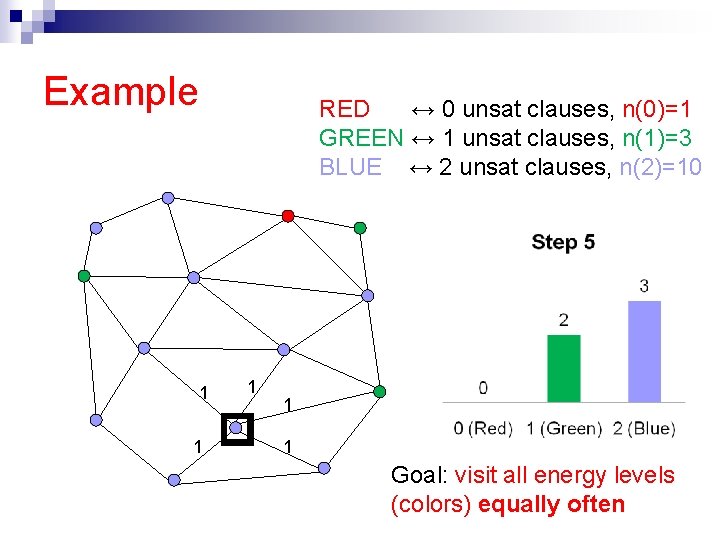
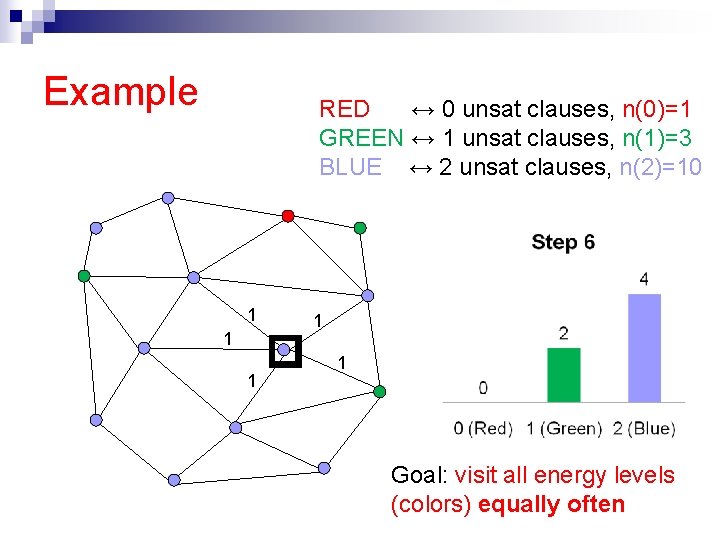
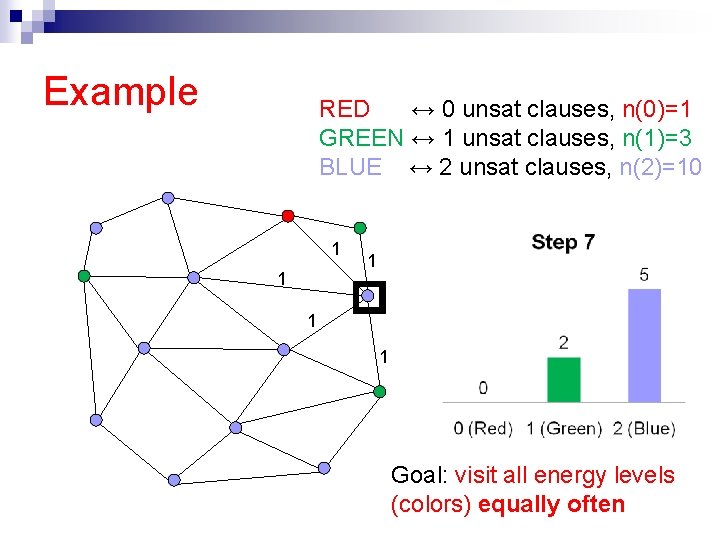
The flat histogram idea n Idea: Set up a Markov Chain that visits all energy levels equally often [F. Wang and Landau ’ 02, J. Wang et. al. ’ 99, De Oliveira et. al. ’ 96] e. g. an equal amount of time at the set of truth assignments with 0 unsat clauses, 1 unsat clause, . . . n How? Flip a variable, accept new state σ’ with probability n Always accepts “rarer” states (when n(E’)<n(E))

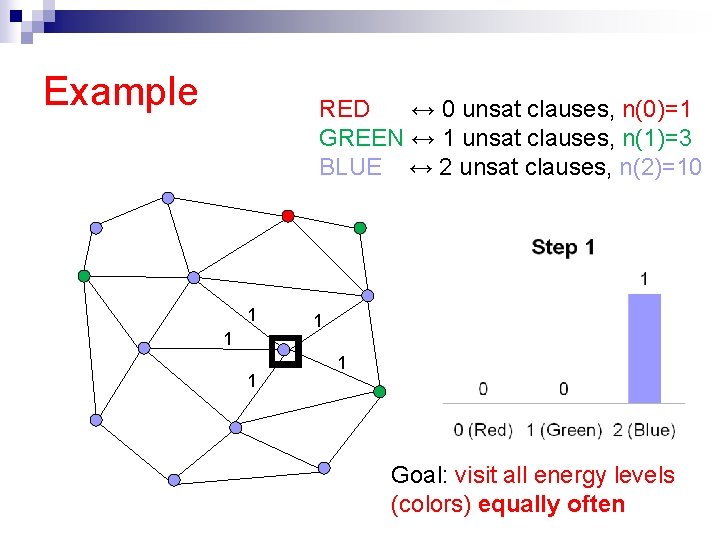
Example RED ↔ 0 unsat clauses, n(0)=1 GREEN ↔ 1 unsat clauses, n(1)=3 BLUE ↔ 2 unsat clauses, n(2)=10 1 1 1 Goal: visit all energy levels (colors) equally often

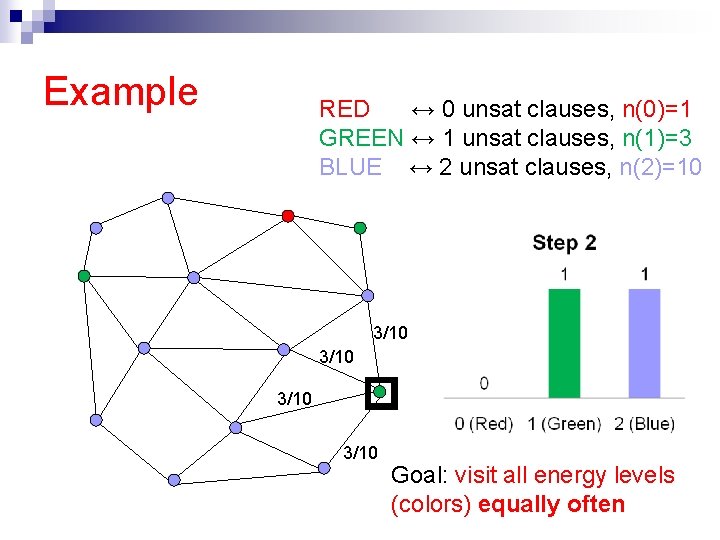
Example RED ↔ 0 unsat clauses, n(0)=1 GREEN ↔ 1 unsat clauses, n(1)=3 BLUE ↔ 2 unsat clauses, n(2)=10 3/10 Goal: visit all energy levels (colors) equally often

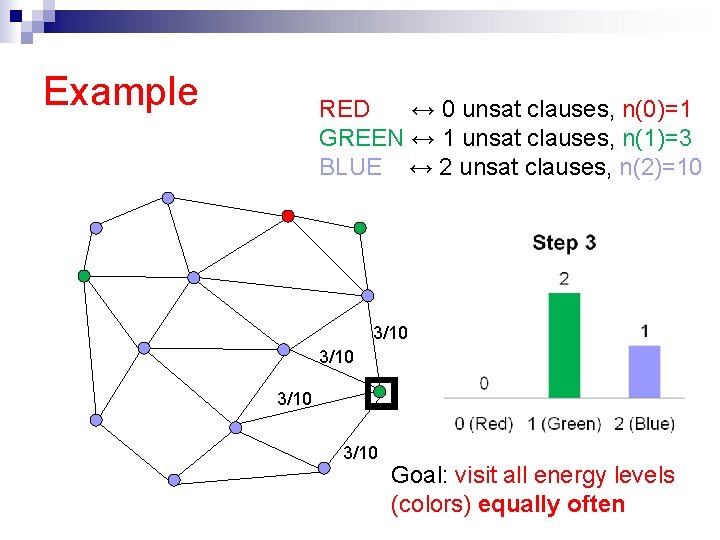
Example RED ↔ 0 unsat clauses, n(0)=1 GREEN ↔ 1 unsat clauses, n(1)=3 BLUE ↔ 2 unsat clauses, n(2)=10 1 1 1 Goal: visit all energy levels (colors) equally often

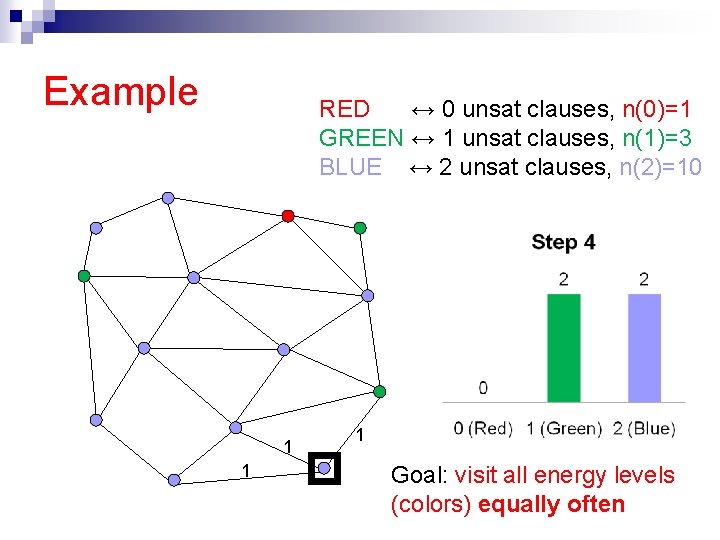
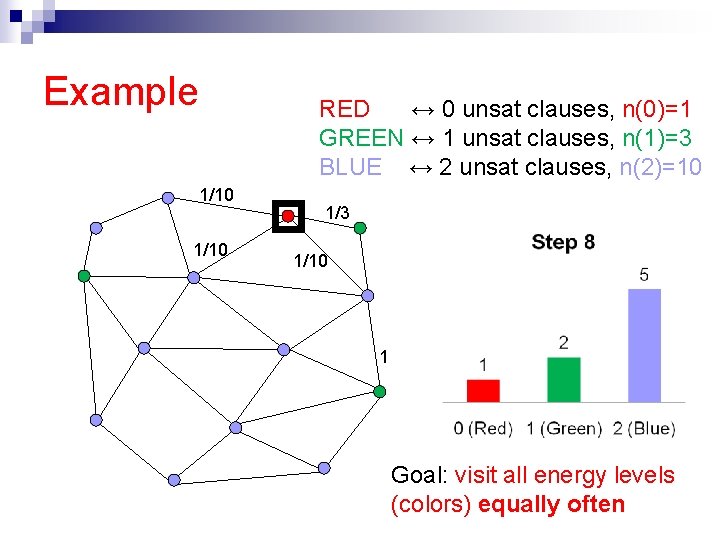
Example RED ↔ 0 unsat clauses, n(0)=1 GREEN ↔ 1 unsat clauses, n(1)=3 BLUE ↔ 2 unsat clauses, n(2)=10 1/10 1/3 1/10 1 Goal: visit all energy levels (colors) equally often

Example …and finally…

Example RED ↔ 0 unsat clauses, n(0)=1 GREEN ↔ 1 unsat clauses, n(1)=3 BLUE ↔ 2 unsat clauses, n(2)=10

Flat histogram: Intuition n Detailed balance holds with those transition probabilities n Properly biased towards “rare” states But there are few “rare” states n (Red, Blue, Green) The total time spent in each type of state is the same (flat visit histogram). Note: in contrast, Simulated Annealing concentrates sampling around low energy states (more greedy!)

Flat histogram But… how can we even run the Markov Chain? Acceptance probability: The density n() is unknown and is precisely what we want to compute!

Adaptive sampling n n Start with an initial guess g (our estimate of the true density n) Random walk: ¨ Use g for guidance (acceptance probability) ¨ Chain will initially not sample uniformly across energy levels ¨ Each step, adjust g using a modification factor F ¨ Keep track of the visit histogram H n When we see a flat H, we must have the right density!

The modification factor, F n n F controls the tradeoff between convergence rate and accuracy Use large modification factors F at the beginning to get ¨ rough estimates ¨ fast convergence n n Keep reducing F to get finer estimates Analogous to an annealing process

MCMC-Flat. Sat Initialization Inner Loop : adaptive sampling until the visit histogram is flat (g becomes our new guess for n)

MCMC-Flat. Sat Outer Loop Reduce modification factor and repeat inner loop until g≈n

Outline of empirical validation n Empirical validation on combinatorial problems ¨ Convergence ¨ Efficiency (number ¨ Accuracy n of samples vs search space size) We study: ¨ Small formulas with ground ¨ Large synthetic formulas ¨ Random 3 -SAT ¨ Large structured instances ¨ Model counting truth

Formulas with known ground truth n n n Instances from MAXSAT 2007 competition (Ramsey, Spin Glass, Max Clique) Direct enumeration is possible (n<=28), so we can compare our estimate with ground truth Metrics: ¨ KL divergence: ¨ Relative error per point

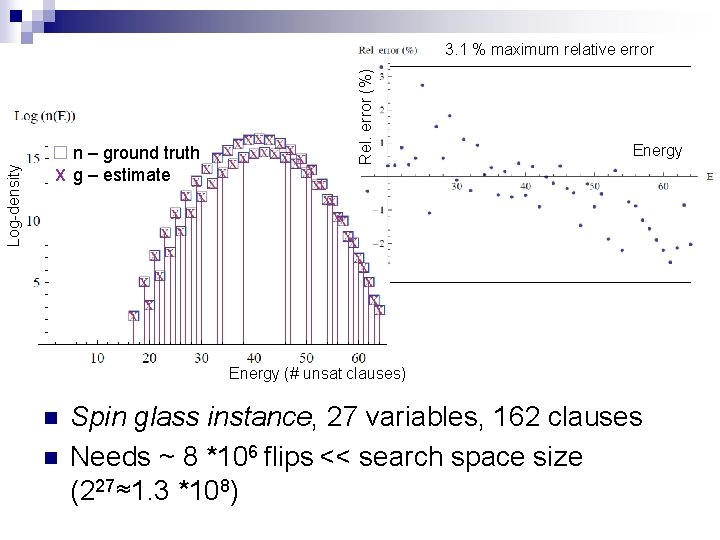
n – ground truth X g – estimate Rel. error (%) Log-density 3. 1 % maximum relative error Energy (# unsat clauses) n n Spin glass instance, 27 variables, 162 clauses Needs ~ 8 *106 flips << search space size (227≈1. 3 *108)

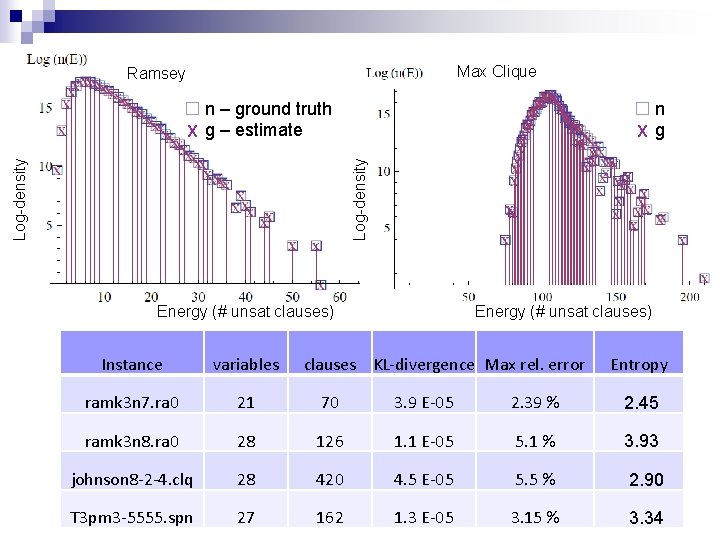
Max Clique Ramsey n X g Log-density n – ground truth X g – estimate Energy (# unsat clauses) Instance variables clauses KL-divergence Max rel. error Entropy ramk 3 n 7. ra 0 21 70 3. 9 E-05 2. 39 % 2. 45 ramk 3 n 8. ra 0 28 126 1. 1 E-05 5. 1 % 3. 93 johnson 8 -2 -4. clq 28 420 4. 5 E-05 5. 5 % 2. 90 T 3 pm 3 -5555. spn 27 162 1. 3 E-05 3. 15 % 3. 34

Synthetic formulas n Ground truth for larger formulas? ¨ Construct n n n synthetic formulas Formulas for which we derive a closed form solution for the density Result on the composition (logical conjunction) of independent formulas (do not share variables) The density of F is the convolution of the density of Φ with itself l times

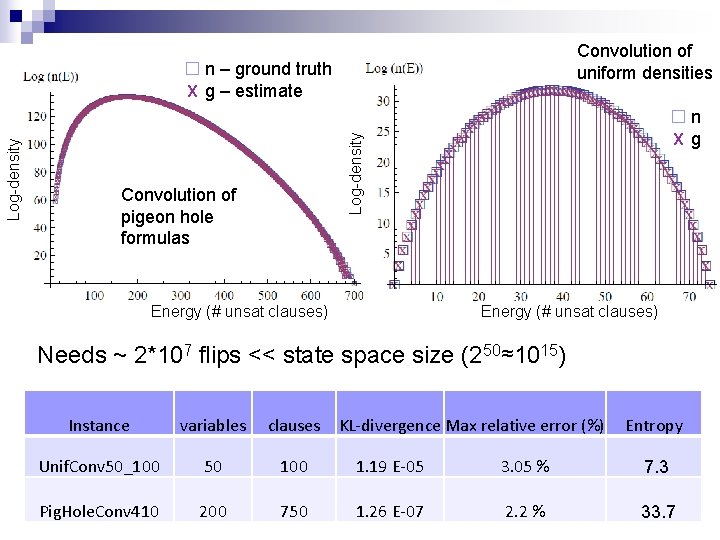
Convolution of uniform densities n X g Log-density n – ground truth X g – estimate Convolution of pigeon hole formulas Energy (# unsat clauses) Needs ~ 2*107 flips << state space size (250≈1015) Instance variables clauses KL-divergence Max relative error (%) Entropy Unif. Conv 50_100 50 100 1. 19 E-05 3. 05 % 7. 3 Pig. Hole. Conv 410 200 750 1. 26 E-07 2. 2 % 33. 7

Random k-SAT formulas n n Well known phase transitions for the satisfiability property in terms of the ratio α (Φ is satisfiable ↔ nΦ(0)>0 ) Analytic result on the average density given a truth assignment, the probability of having a clause that is violated is 1/2 k for random k-SAT

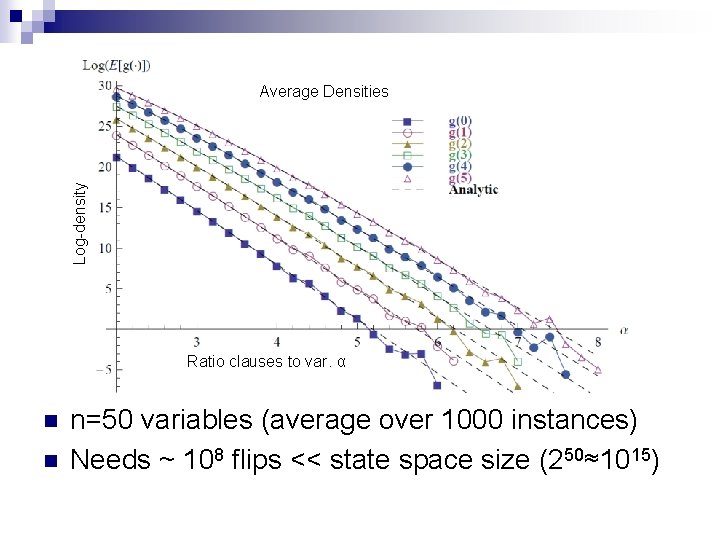
Log-density Average Densities Ratio clauses to var. α n n n=50 variables (average over 1000 instances) Needs ~ 108 flips << state space size (250≈1015)

Large structured instances n n No ground truth known Consistency checks ¨ Number of models, when exact model counting is feasible (# models=n(0)) ¨ Method of the moments: n Sample K assignments at random, compute their energies (unsat clauses) n Compute sample moments (e. g. average energy, 2 nd order moment of energy, . . ) n Compare with moments obtained using the estimated density g

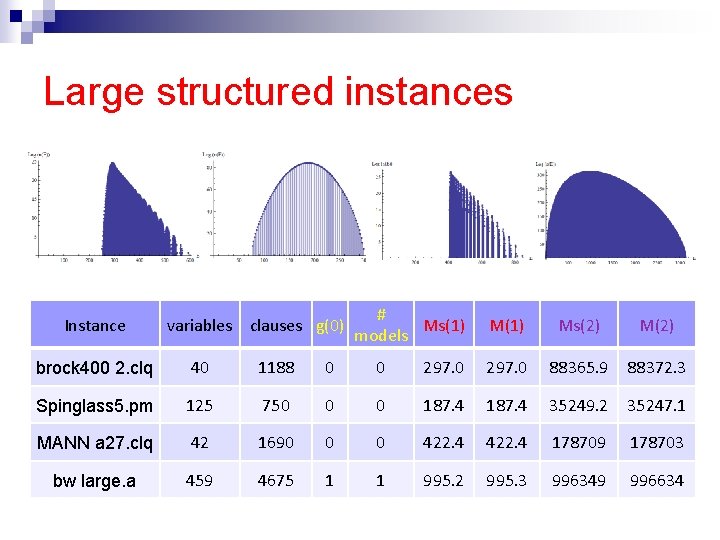
Large structured instances Instance variables clauses g(0) # Ms(1) models M(1) Ms(2) M(2) brock 400 2. clq 40 1188 0 0 297. 0 88365. 9 88372. 3 Spinglass 5. pm 125 750 0 0 187. 4 35249. 2 35247. 1 MANN a 27. clq 42 1690 0 0 422. 4 178709 178703 bw large. a 459 4675 1 1 995. 2 995. 3 996349 996634

n Planning problem: ¨ n=459 variables ¨ m=4675 clauses Log-density Logistic instance Energy (# unsat clauses) n n Huge search space (2459 truth assignments), but MCMC-Flat. Sat returns within hours Remarkable precision: ¨ Finds the only existing model g(0)=n(0)=1! ¨ The mode of the estimated distribution is e 300 times larger than the number of models g(0) counts the needles and the haystack! (the moments method indicates g is accurate)

Model counting n Comparison with state-of-the-art model counters ¨ Sample. Count [Gomes et. al. ‘ 06] ¨ Sample. Mini. SAT [Gogate et. al. ‘ 07] n n MCMCFlat. Sat is very accurate Timings are competitive when ratio clauses to variables is not too large ¨ DOS provides guidance ¨ Information on what is not a model ¨ Overhead because it provides more information

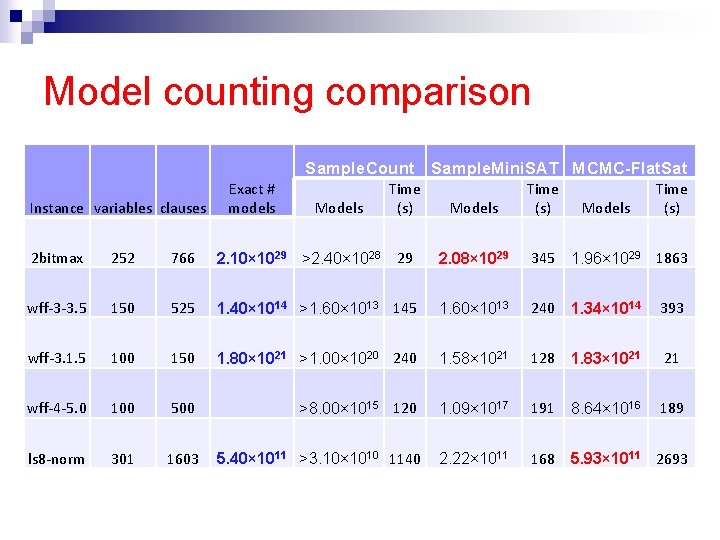
Model counting comparison Sample. Count Sample. Mini. SAT MCMC-Flat. Sat Instance variables clauses Exact # models Models Time (s) 2 bitmax 252 766 2. 10× 1029 >2. 40× 1028 29 2. 08× 1029 345 1. 96× 1029 1863 wff-3 -3. 5 150 525 1. 40× 1014 >1. 60× 1013 145 1. 60× 1013 240 1. 34× 1014 393 wff-3. 1. 5 100 150 1. 80× 1021 >1. 00× 1020 240 1. 58× 1021 128 1. 83× 1021 21 wff-4 -5. 0 100 500 >8. 00× 1015 120 1. 09× 1017 191 8. 64× 1016 189 ls 8 -norm 301 1603 5. 40× 1011 >3. 10× 1010 1140 2. 22× 1011 168 5. 93× 1011 2693

Conclusions n n Computing the density of states is a hard problem (encompasses SAT, MAX-SAT, #SAT) MCMCFlat. Sat: sampling strategy adapted from physics for combinatorial spaces that adaptively explores the space while collecting statistics ¨ Extremely accurate, very efficient (few samples) ¨ Provides a compact, rich description of the search space. New insights about structure and local search n Very general method: any property can be used for search space partitioning. ¨ Many applications to counting and inference problems

Extra slides

Future work n SAT-specific improvements ¨ Energy saturation ¨ Energy barriers (and related normalization issues) ¨ Walksat heuristics (with Metropolis-Hastings updates) n n n Direct application to inference in Markov Logic Formal proof of convergence / counterexamples Application to other counting problems in combinatorial spaces

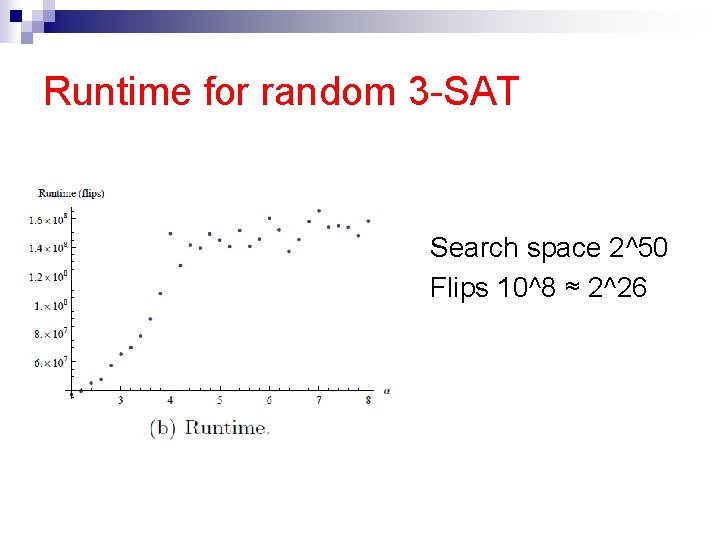
Runtime for random 3 -SAT n n Search space 2^50 Flips 10^8 ≈ 2^26

Related work on random 3 -SAT n Lots of work on the i=0 (i. e. SAT/UNSAT) case [Gent et. al. ‘ 94] n Previous experimental work for i>0 [Zhang ‘ 01] ¨ Different definition: “no more than i unsat clauses” versus “exactly i unsat clauses” ¨ Location on the phase transitions ¨ Apparently, same location n n Analytic results [Achlioptas et al. ‘ 05] We can see two phase transitions: assignments are unlikely to violate a large number of clauses

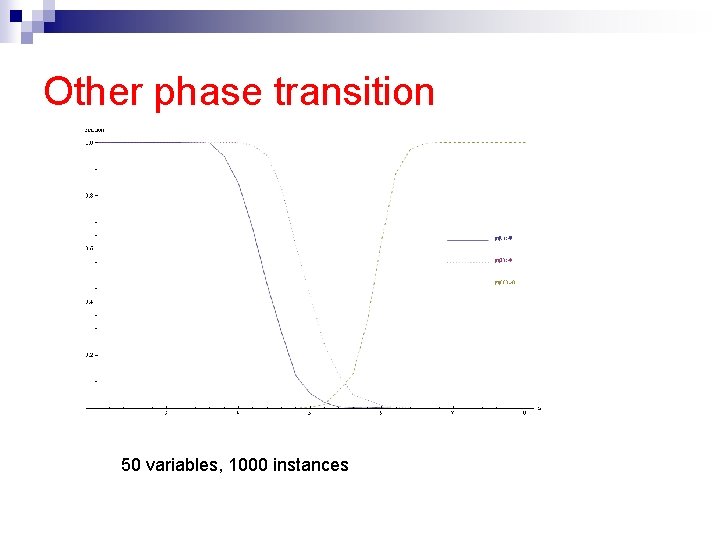
Other phase transition 50 variables, 1000 instances

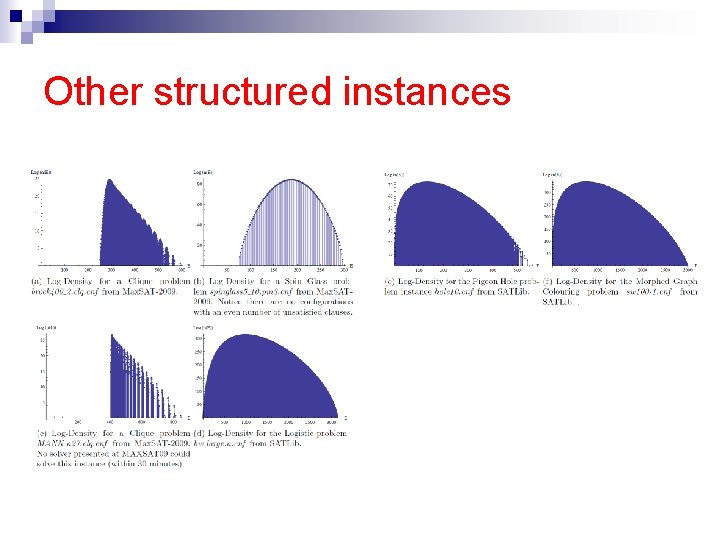
Other structured instances

Histogram flatness (formal) n Flatness condition of the visit histogram H is a necessary condition for convergence ¨ If g is equal to the true density n, the detailed balance is satisfied by upon convergence, the steady state probability is proportional to the reciprocal of the density of the corresponding energy level

Histogram flatness (formal) n Flatness condition of the visit histogram H is a necessary condition for convergence If g=n, the visit histogram H will be flat i. e. energy levels visited equally often n Problem: the density n() is unknown and is precisely what we want to compute!

Propositional Satisfiability (SAT) Satifiability (SAT): Given a formula in propositional calculus, does it have a model, i. e. , is there an assignment to its variables making it true? (a b c) AND (a c) SAT: prototypical hard combinatorial search and reasoning problem. Problem is NP-Complete. (Cook 1971)

Prior work - Metropolis n Approximate [Rose et. al. , ‘ 96 ] ¨ Metropolis sampling at temperature T ¨ Energy = number of violated clauses ¨ Measure the empirical probability P(E) of energy levels, rescale to get the density n(E) ¨ Slow mixing times [Wei et. al. , ‘ 04 ] ¨ Difficult choice of the temperature

Theoretical Convergence n Stated as a conjecture in Lee, Okabe and Landau, Convergence and Refinement of the Wang-Landau Algorithm, Computer Physics Communications, 2006 n Proof of convergence in Atchade and Liu, The Wang-Landau Algorithm for Monte Carlo computation in general state spaces, Statistica Sinica, 2009

Closed forms n k-SAT, m clauses such that each variable appears exactly in one clause, the DOS is where is the fraction of assignments of the variables in a single clause not satisfying it (e. g. in 3 -SAT, only 1 over 8 assignments does not satisfy a clause)

Implementation details n n Use of log-densities New assignment generated by flipping a variable uniformly at random Flatness condition (within 10% of the max) Normalization ¨ The density is obtained only up to a constant factor ¨ We use the normalization constraint n n F 0=1. 5, reduce by Flatness is checked every 1000 moves

Random k-SAT formulas n n k-SAT: each clause has at most k literals Random k-SAT: formulas Φ generated with ¨n variables ¨ m clauses produced independently by n n ¨α n randomly choosing a set of k variables from n available negating each one with probability 0. 5 is the ratio clauses to variables (m/n) Let be the probability measure associated with this generative model for Φ

Composition n Logical conjunction of formulas Φ that do not share variables n The density of F is the convolution of the density of Φ with itself l times Analogous to the probability density of the sum of l independent random variables n

Closed forms n Starting with a formula Φ with uniform density (e. g. ) we construct Sum of n s-sided dices has closed form probability distribution: