Computing Shortest Paths among Curved Obstacles in the

Computing Shortest Paths among Curved Obstacles in the Plane Danny Z. Chen 1 and Haitao Wang 2 1 University of Notre Dame 2 Utah State University So. CG 2013

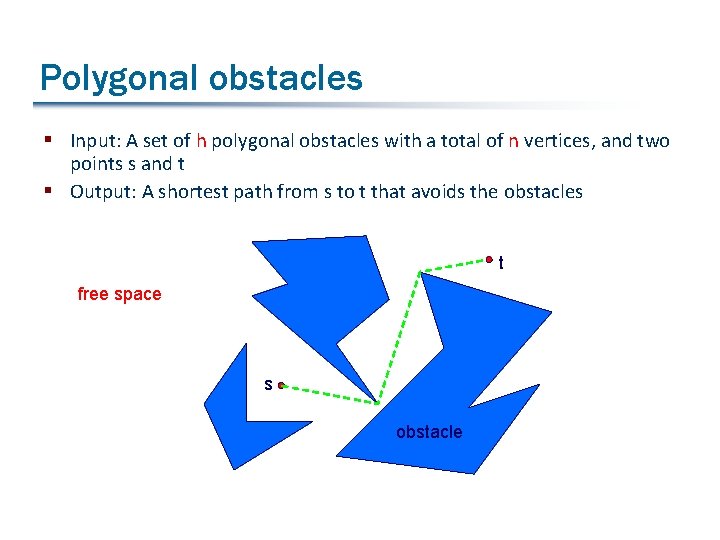
Polygonal obstacles § Input: A set of h polygonal obstacles with a total of n vertices, and two points s and t § Output: A shortest path from s to t that avoids the obstacles t free space s obstacle

Curved obstacles § Input: a set of obstacles whose boundaries are curves § Output: a shortest path from s to t in the free space t s

Modeling curved obstacles § An obstacle: a simple region with vertices on the boundary § The boundary portion between two adjacent vertices is of constant size

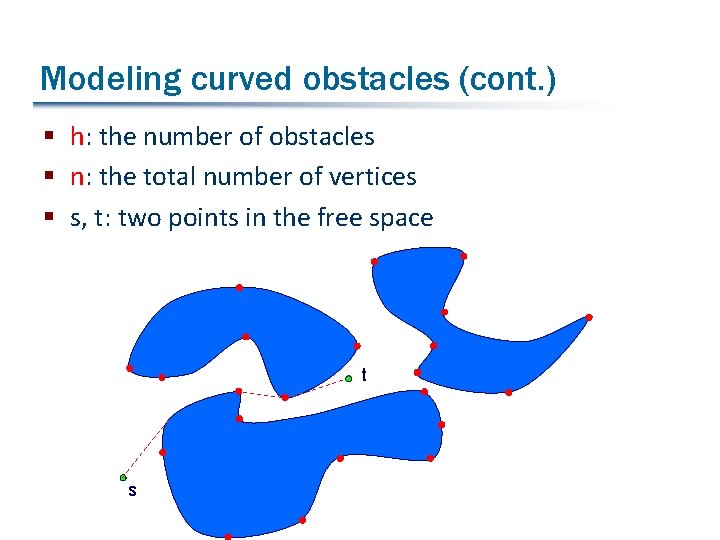
Modeling curved obstacles (cont. ) § h: the number of obstacles § n: the total number of vertices § s, t: two points in the free space t s

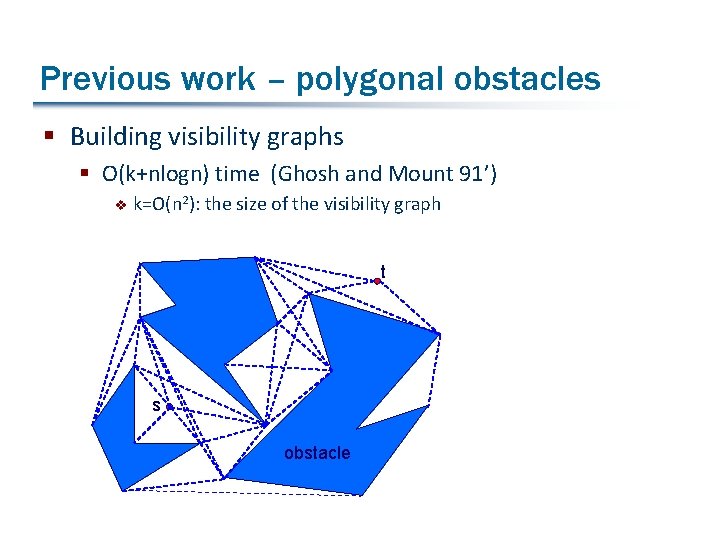
Previous work – polygonal obstacles § Building visibility graphs § O(k+nlogn) time (Ghosh and Mount 91’) v k=O(n 2): the size of the visibility graph t s obstacle

Previous work – polygonal obstacles § Building visibility graphs § O(k+nlogn) time (Ghosh and Mount 91’) v k=O(n 2): the size of the visibility graph § Continuous Disjkstra scheme § O(n 1. 5+Є) time (Mitchell 96’) v first sub-quadratic algorithm § O(nlogn) time and space (Hershberger and Suri 99’) v time-optimal

Curved obstacles – previous and new results § Convex case: all obstacles are convex § Chew 85’, Chang et al. 05’, Hershberger and Guibas 88’, Storer and Reif 94’ § O(n 2) time (Chen and Wang 11’) § Non-convex case: § the previous talk, Hershberger, Suri, and Yildiz v Approach: continuous Dijkstra § our result: O(n+hlog 1+Єh+k) time k=O(h 2): sensitive to the input v Approach: visibility graph v

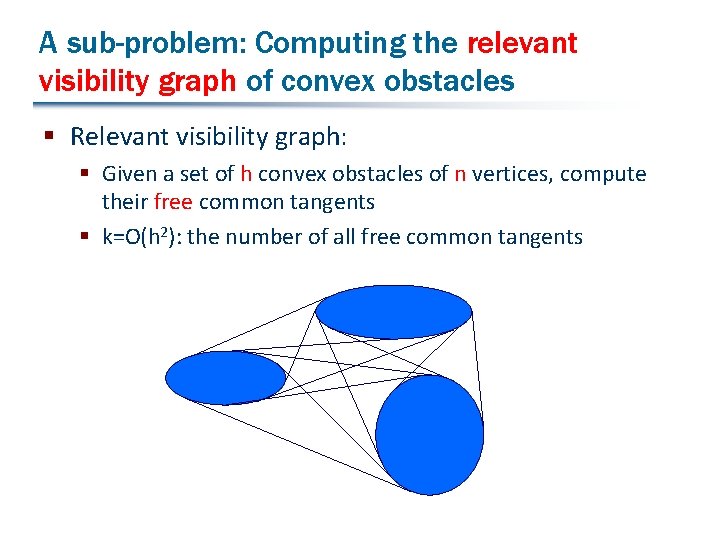
A sub-problem: Computing the relevant visibility graph of convex obstacles § Relevant visibility graph: § Given a set of h convex obstacles of n vertices, compute their free common tangents § k=O(h 2): the number of all free common tangents

Previous work and our result § For polygonal convex obstacles: § O(n + h 2 logn) time, Rohnert, 96’; Kapoor, Maheshwari, Mitchell, 97’ § An open question: O(n + klogn) time § O(nlogn+k) time, Pocchiola and Vegter, 95’ § h=n § Each obstacle is of constant size § Our result: O(n+hlogh + k) time and O(n) working space § Better than the open question § Optimal solution

Our algorithm § Reduce the problem to the convex case § the corridor structure, generalizing the polygon case (Kapoor, Maheshwari, Mitchell 97’) § Solve the convex case s t

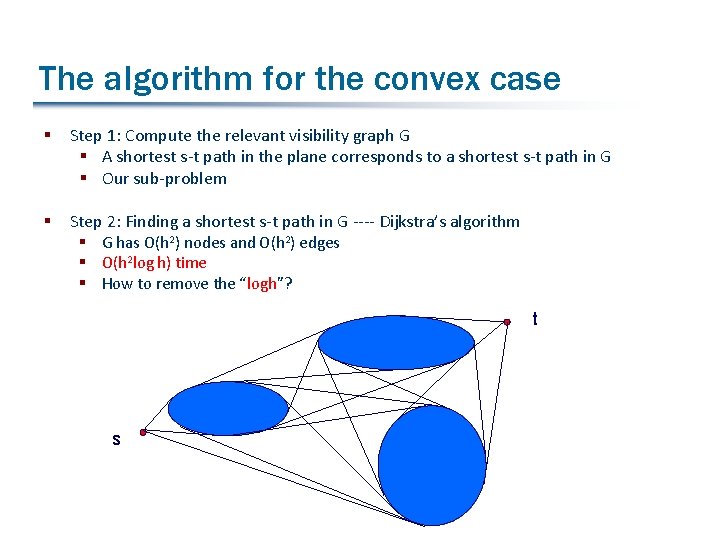
The algorithm for the convex case § Step 1: Compute the relevant visibility graph G § A shortest s-t path in the plane corresponds to a shortest s-t path in G § Our sub-problem § Step 2: Finding a shortest s-t path in G ---- Dijkstra’s algorithm § G has O(h 2) nodes and O(h 2) edges § O(h 2 log h) time § How to remove the “logh”? t s

Solving Step 2 (Chen and Wang 11’) § A follow-up of the work by Hershberger and Guibas 88’ § Transform G to a smaller graph G’ such that § A shortest s-t path in G ↔ a shortest s-t path in G’ § G’ has O(h 2) edges but only O(h) nodes § O(h 2) time for Dijkstra’s algorithm on G’

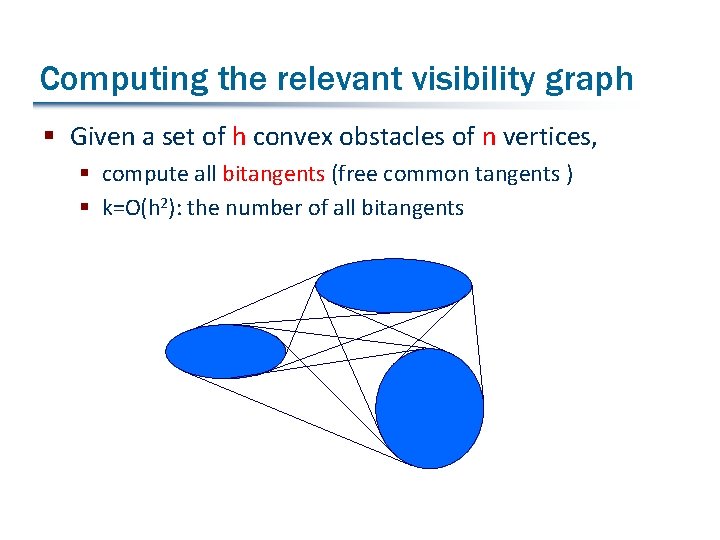
Computing the relevant visibility graph § Given a set of h convex obstacles of n vertices, § compute all bitangents (free common tangents ) § k=O(h 2): the number of all bitangents

The algorithm § An extension of Pocchiola and Vegter’s algorithm (called the PV algorithm) § h=n and all obstacles are of constant size § O(nlogn+k) time and O(n) space § Our result: O(n+hlogh+k) time and O(n) space § Similar to the PV algorithm with some modifications § Challenge: the time analysis PV algorithm: local analysis v Ours: global analysis v

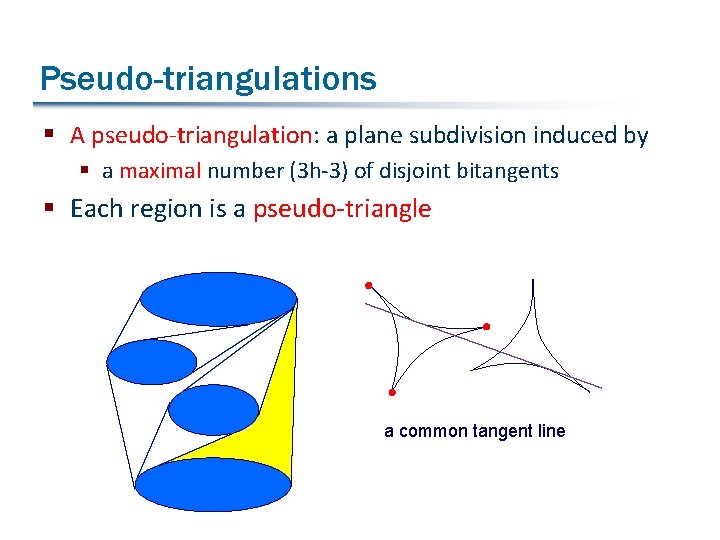
Pseudo-triangulations § A pseudo-triangulation: a plane subdivision induced by § a maximal number (3 h-3) of disjoint bitangents § Each region is a pseudo-triangle a common tangent line

The topological flip algorithm § Start from a pseudo-triangulation T § Flip operations: flip a bitangent b § insert the bitangent b’ of the two pseudo-triangles incident to b § remove b from T § obtain another pseudo-triangulation T’ § Repeat the flip operations § Two issues: § Start from which pseudo-triangulation? § Which is the next bitangent to flip? b b’

Handle the first issue: the initial pseudo-triangulation T 0 § Let B be the set of all bitangents § T 0 is induced by the following bitangents b 1 b 2 b 3 …. § § b 1 is the bitangent of the smallest slope in B b 2 is the bitangent of the smallest slope in B that does not intersect b 1 b 3 is the bitangent of the smallest slope in B that does not intersect b 1 or b 2 …. . b 1 b 3 b 2

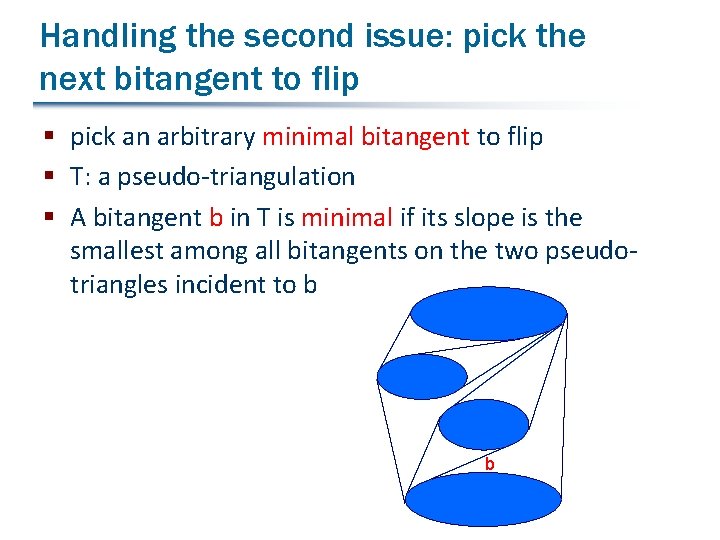
Handling the second issue: pick the next bitangent to flip § pick an arbitrary minimal bitangent to flip § T: a pseudo-triangulation § A bitangent b in T is minimal if its slope is the smallest among all bitangents on the two pseudotriangles incident to b b

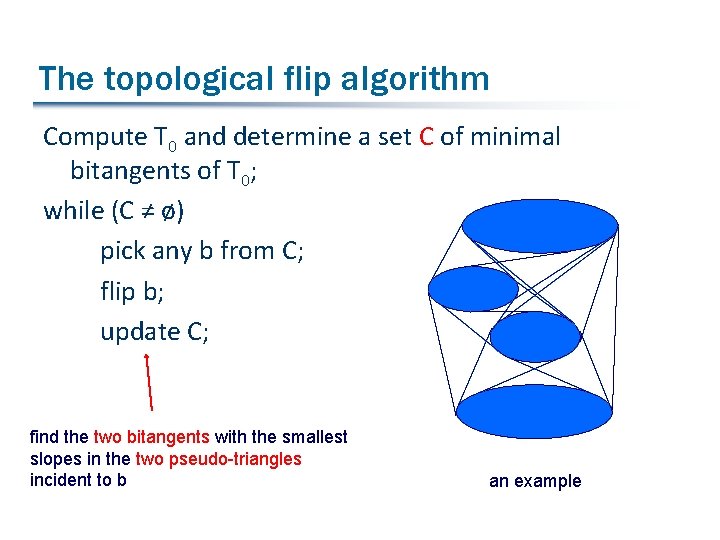
The topological flip algorithm Compute T 0 and determine a set C of minimal bitangents of T 0; while (C ≠ ø) pick any b from C; flip b; update C; find the two bitangents with the smallest slopes in the two pseudo-triangles incident to b an example

Implementation § Key: implement the flip operations efficiently § Goal: O(n+k) time for all k flip operations § Consider a flip on b § a naive approach: start from b, walk clockwise on the boundaries of the two pseudo-triangles incident to b synchronously § time-consuming § an improvement: “jump” to certain locations of the boundaries to start the walk

Time analysis § Implement all walks in the entire algorithm in O(n+k) time § Key: prove that there a total of O(n+k) arcs and bitangents passed by the walks

Proving the total walked arcs and bitangents is O(n+k) § There are k flips in total § Each flip needs to walk on a constant number of bitangents and boundary portions on obstacles § a bitangent v needs O(1) time § a boundary portion of an obstacle v may need Ω(n) time as the portion may be of size Ω(n) s O(1) time for the PV algorithm as each obstacle is of constant size s need a global time analysis for our problem

Conclusions § An O(n+hlog 1+Є h+k) time algorithm for finding shortest paths among curved obstacles § k=O(h 2): sensitive to the input § A sub-problem: Computing the relevant visibility graph § O(n + hlogh +k) time and O(n) working space § Applicable to polygonal obstacles