Computing Maximum NonCrossing Matching in Convex Bipartite Graphs

Computing Maximum Non-Crossing Matching in Convex Bipartite Graphs Danny Z. Chen, Xiaomin Liu, and Haitao Wang University of Notre Dame Indiana, USA FAW-AAIM 2012, Beijing, China

Bipartite Graphs

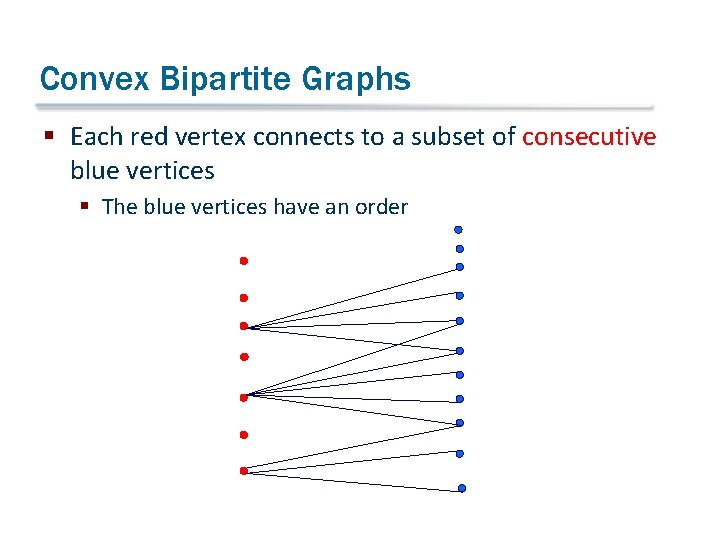
Convex Bipartite Graphs § Each red vertex connects to a subset of consecutive blue vertices § The blue vertices have an order

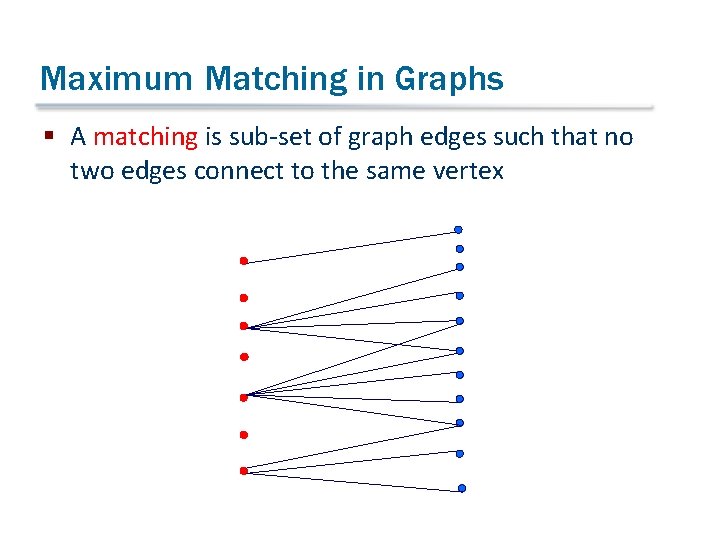
Maximum Matching in Graphs § A matching is sub-set of graph edges such that no two edges connect to the same vertex

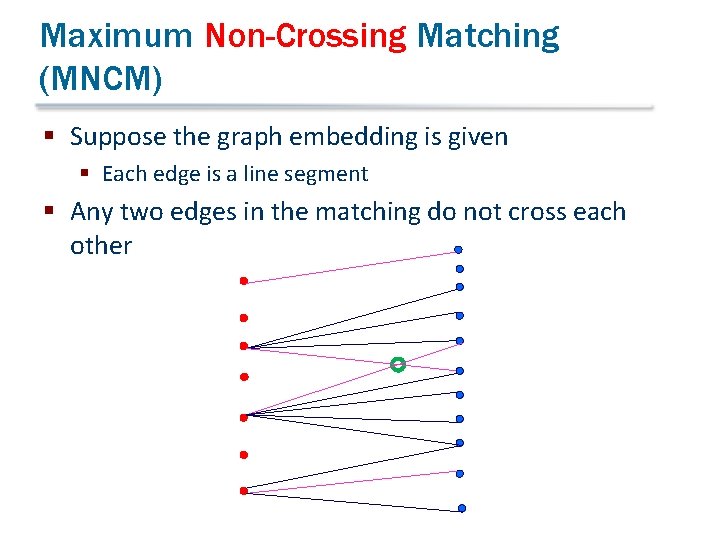
Maximum Non-Crossing Matching (MNCM) § Suppose the graph embedding is given § Each edge is a line segment § Any two edges in the matching do not cross each other

Problem Definition § Given a convex bipartite graph of n vertices and m edges G § Represented implicitly in O(n) space, despite m=ϴ(n 2) § Give the top and bottom edges of each red vertex § Goal: find a maximum non-crossing matching in G top edge bottom edge

Motivation § A sub-problem in our study of medical imaging § Applications in VLSI design

Previous Work § Proposed by Kajitami and Takahashi, 86’ (Symp. On Circuits and Systems) § O(n 2) time algorithm § Reduce it to the problem of finding the longest increasing subsequence in a permutation of size m § O(mlog n) time, Fredman 75’, Widmayer and Wong, 82’ § Malucelli, Ottamann, and Pretolani, 93’ (Discrete Applied Mathmatics) § A labeling algorithm v O(mloglog n) time for general bipartite graphs § O(m+nlog n) time for convex bipartite graphs

Our Result § Convex bipartite graphs § O(nlog n) time § The approaches § Based on the labeling algorithm § New observations § A new data structure

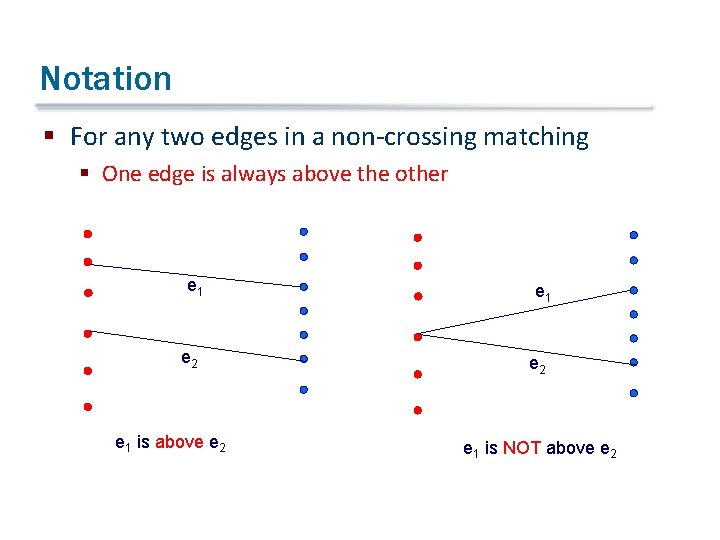
Notation § For any two edges in a non-crossing matching § One edge is always above the other e 1 e 2 e 1 is above e 2 e 1 is NOT above e 2

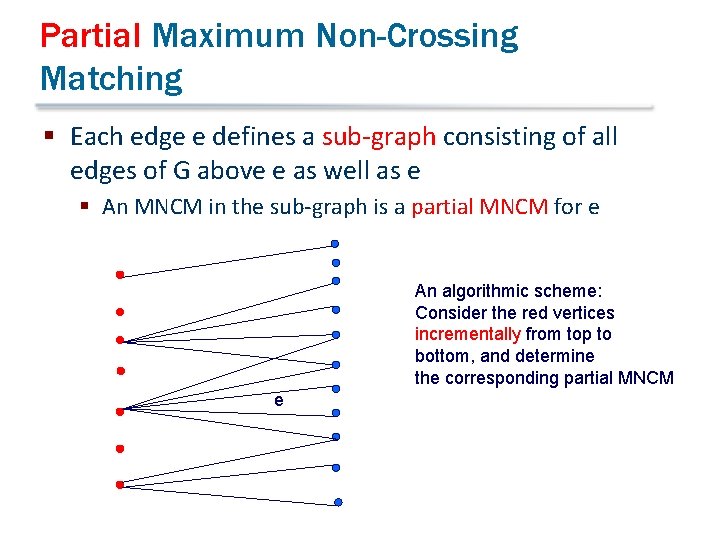
Partial Maximum Non-Crossing Matching § Each edge e defines a sub-graph consisting of all edges of G above e as well as e § An MNCM in the sub-graph is a partial MNCM for e An algorithmic scheme: Consider the red vertices incrementally from top to bottom, and determine the corresponding partial MNCM e

An intuition

The Labeling Algorithm (Previous Work) § A label for each edge e: the size of the partial MNCM of e § A label for each blue vertex: the largest label of the incident edges of the blue vertex 1 1 2 2 u 2 3 3 3 2 3 Rule: the label value of the edge equals one plus the largest label of the blue vertices above u O(mlog n) time: priority search tree

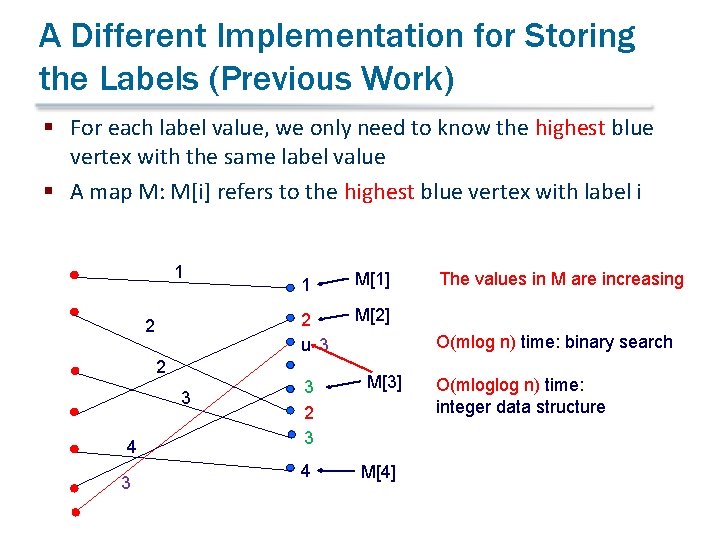
A Different Implementation for Storing the Labels (Previous Work) § For each label value, we only need to know the highest blue vertex with the same label value § A map M: M[i] refers to the highest blue vertex with label i 1 2 2 3 4 3 1 M[1] 2 u 3 M[2] 3 2 3 4 The values in M are increasing O(mlog n) time: binary search M[3] M[4] O(mloglog n) time: integer data structure

A New Observation for Updating M on Convex Bipartite Graphs (Our Work) M[i] top edge i+1 M[i+1] i+2 v i+3 M[i+2] M[i+3] i+4 bottom edge M[i+4]

A New Observation for Updating C (cont. ) M[i] … … M[i+1] M[h] M[i+2]=1+M[i+1] …… … v Update M … M[h-1]=1+M[h-2] … M[h]=1+M[h-1] M[h+1]=1+M[h] a range-shift operation

A New Data Structure § Storing the elements in M § Implementing the range-shift operations § O(log n) time § The segment tree does not work § Because insertions and deletions are involved in the range -shift operations § Overall running time of the algorithm: O(nlog n)

Finding an Actual MNCM § Our algorithm computes the map M § With M, find an actual MNCM § Previous work: O(m) time, m=ϴ(n 2) § Our new result: O(n) time, a greedy algorithm § The key: one particular red vertex § The lowest red vertex in an MNCM § The map M is not needed!

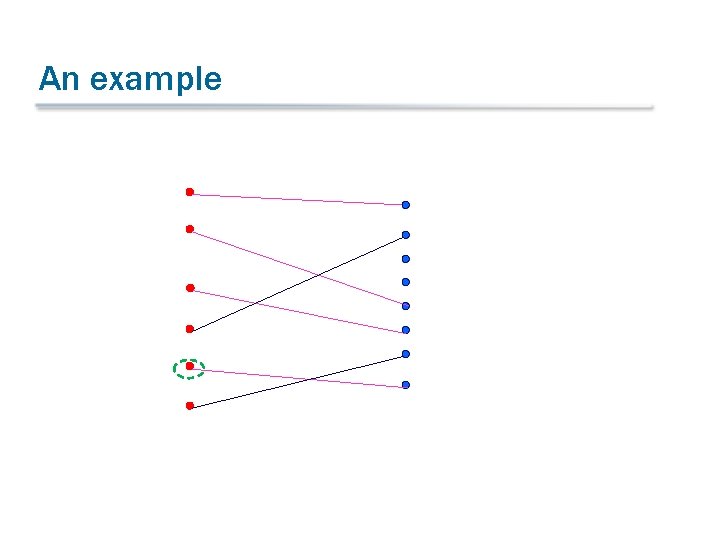
An example

Conclusion § A new algorithm for computing MNCM in convex bipartite graphs § O(nlog n) time § Previous work: O(m+nlog n), m=O(n 2) § Open problem: § A maximum matching can be found in O(n) time § Can we find an MNCM in O(n) time? v Determining the particular red vertex looks easier?

Thank you