Computing Functions with Turing Machines 1 A function

Computing Functions with Turing Machines 1

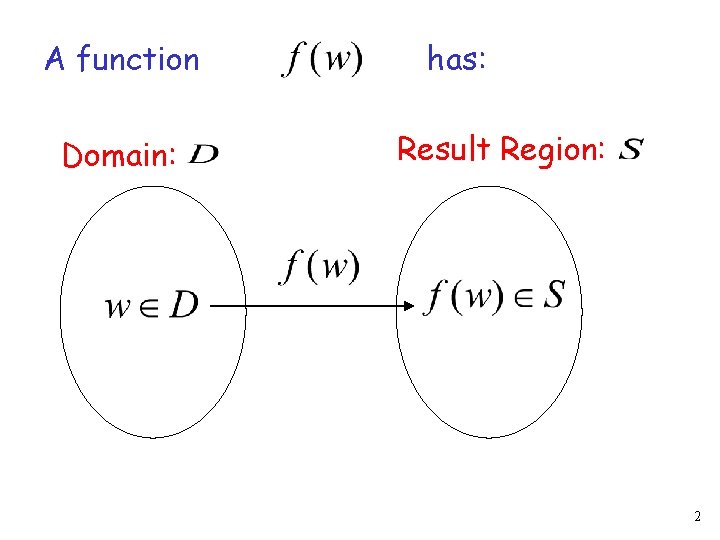
A function Domain: has: Result Region: 2

A function may have many parameters: Example: Addition function 3

Integer Domain Decimal: 5 Binary: 101 Unary: 11111 We prefer unary representation: easier to manipulate with Turing machines 4

Definition: A function is computable if there is a Turing Machine such that: Initial configuration Final configuration initial state For all final state Domain 5

In other words: A function is computable if there is a Turing Machine such that: Initial Configuration For all Final Configuration Domain 6

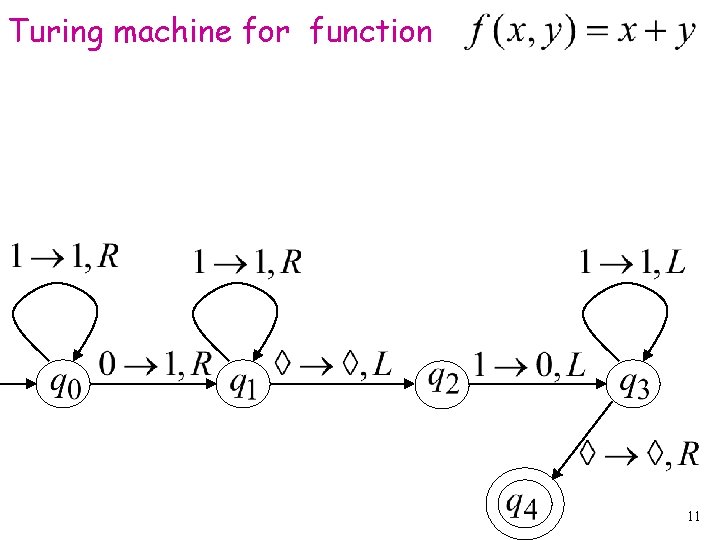
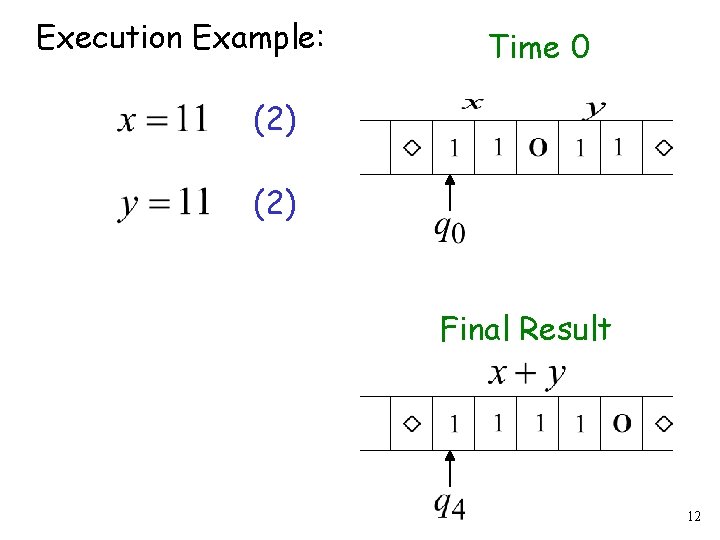
Example The function is computable are integers Turing Machine: Input string: unary Output string: unary 7

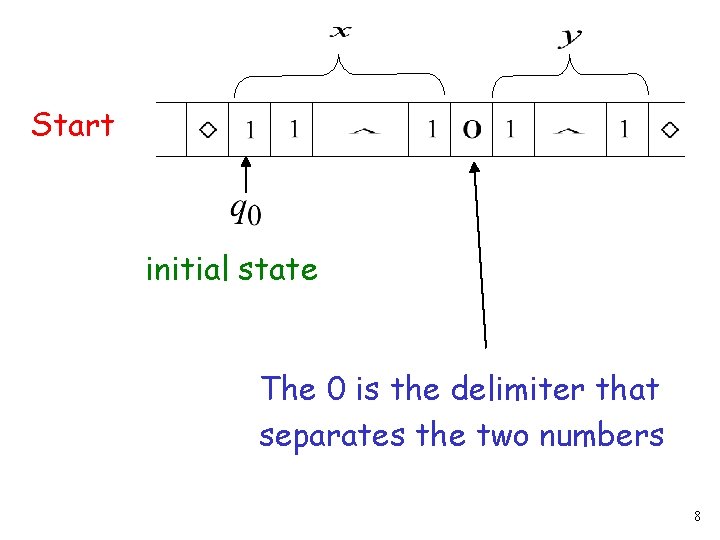
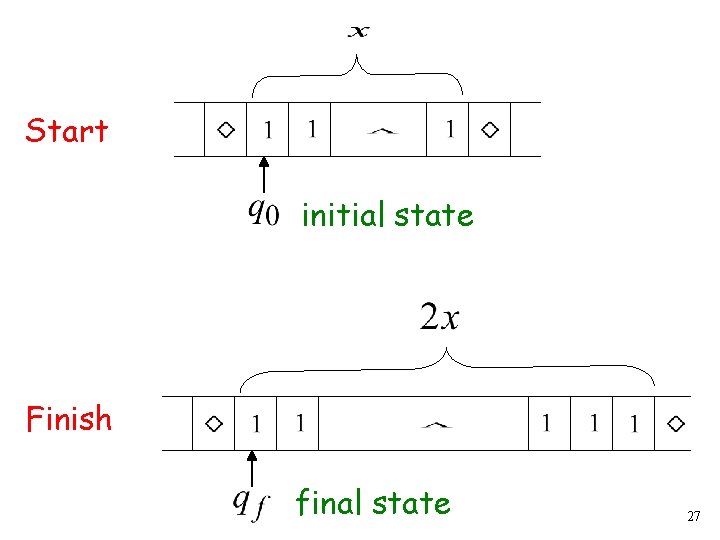
Start initial state The 0 is the delimiter that separates the two numbers 8

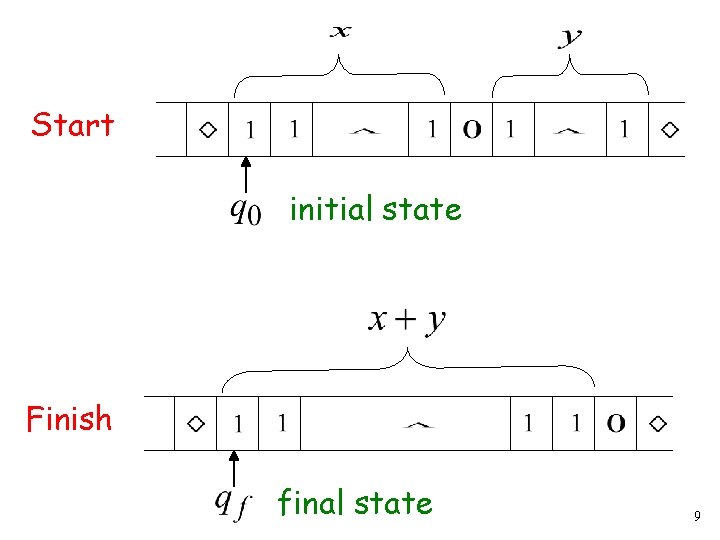
Start initial state Finish final state 9

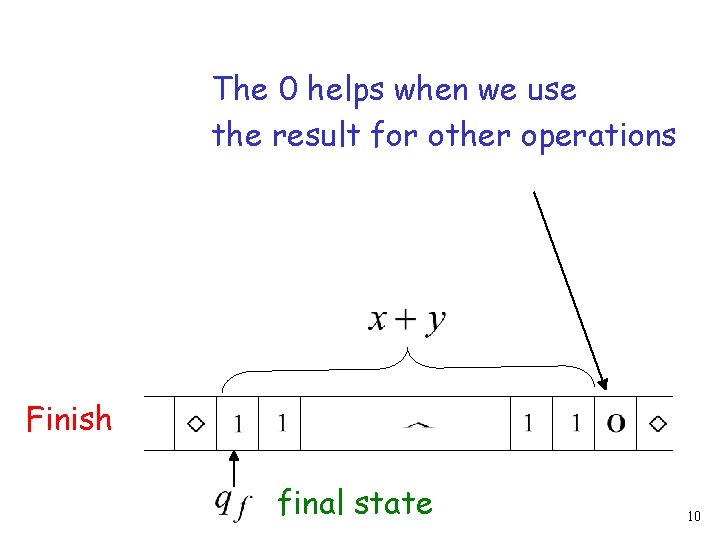
The 0 helps when we use the result for other operations Finish final state 10

Turing machine for function 11

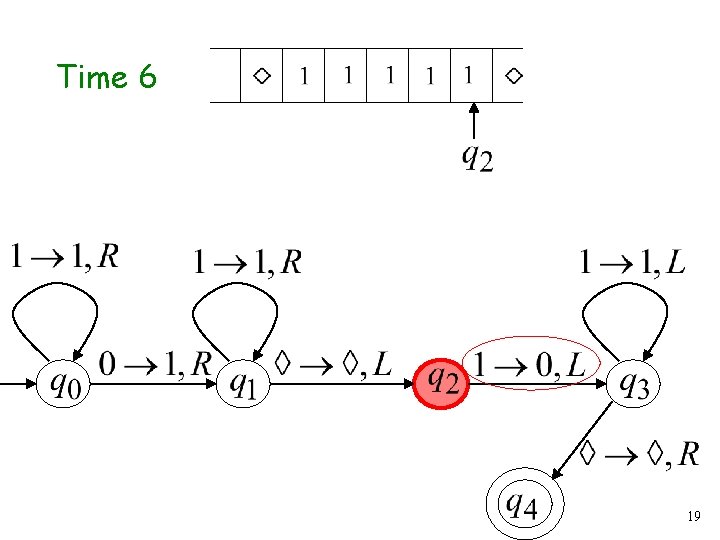
Execution Example: Time 0 (2) Final Result 12

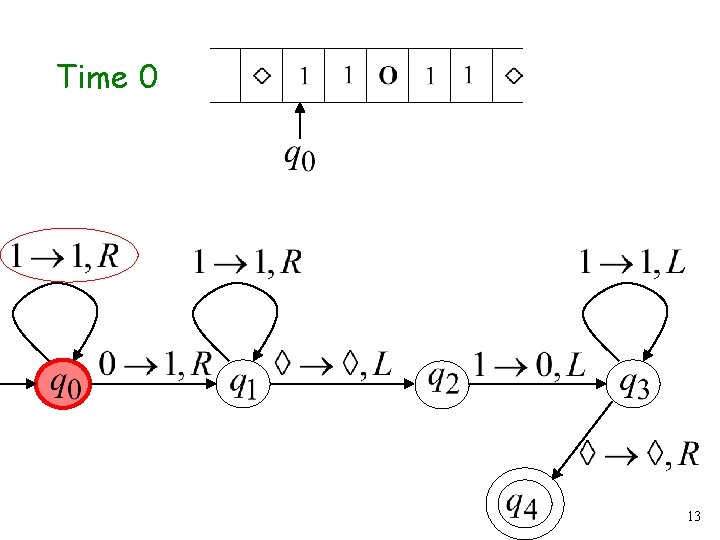
Time 0 13

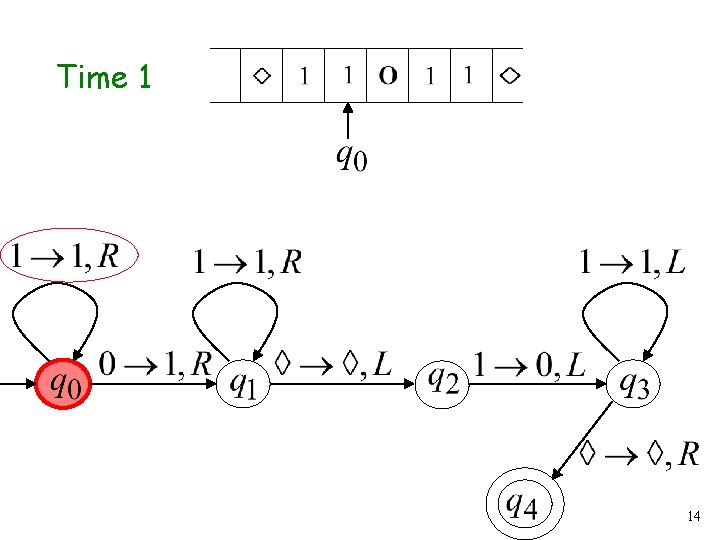
Time 1 14

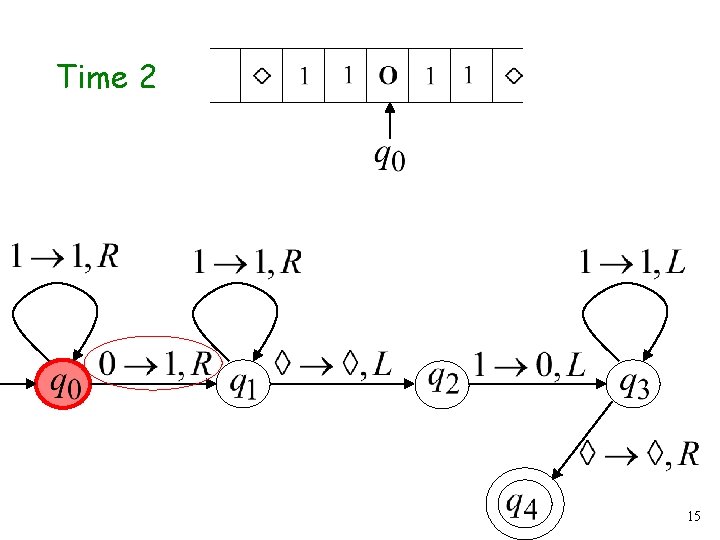
Time 2 15

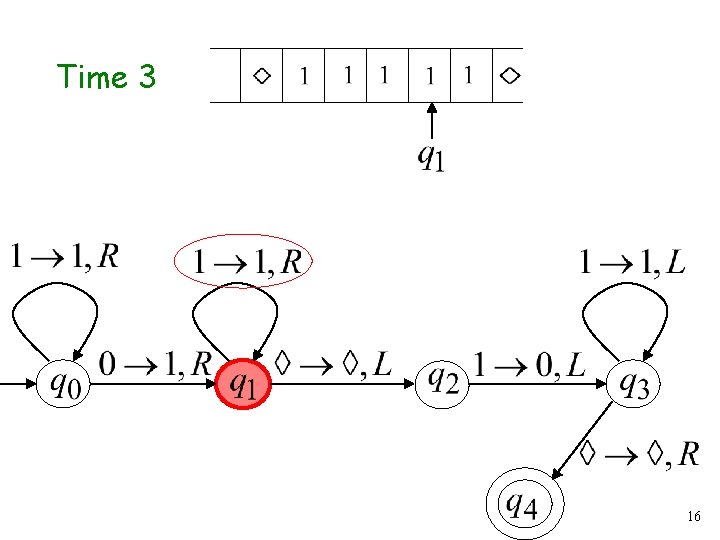
Time 3 16

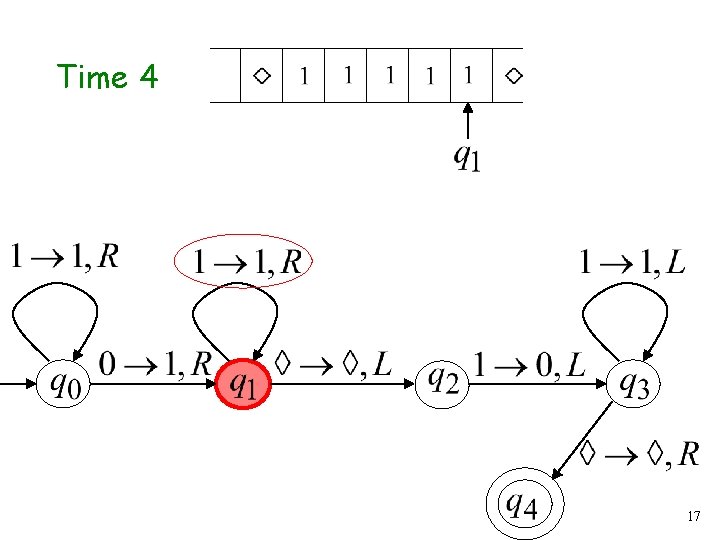
Time 4 17

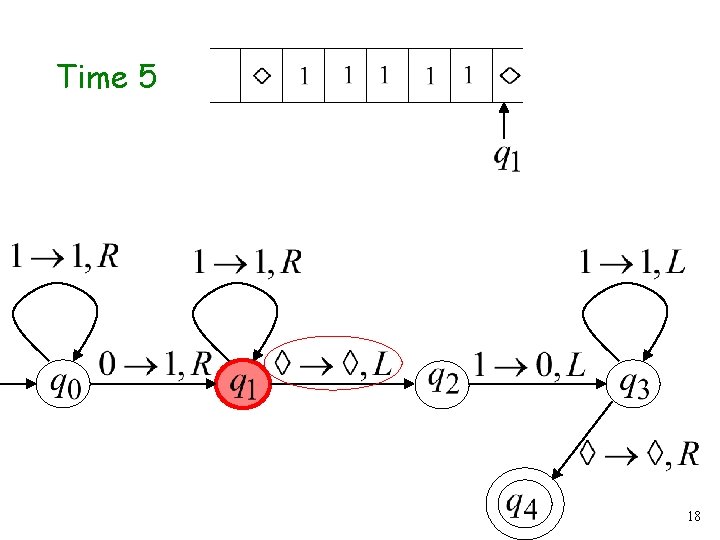
Time 5 18

Time 6 19

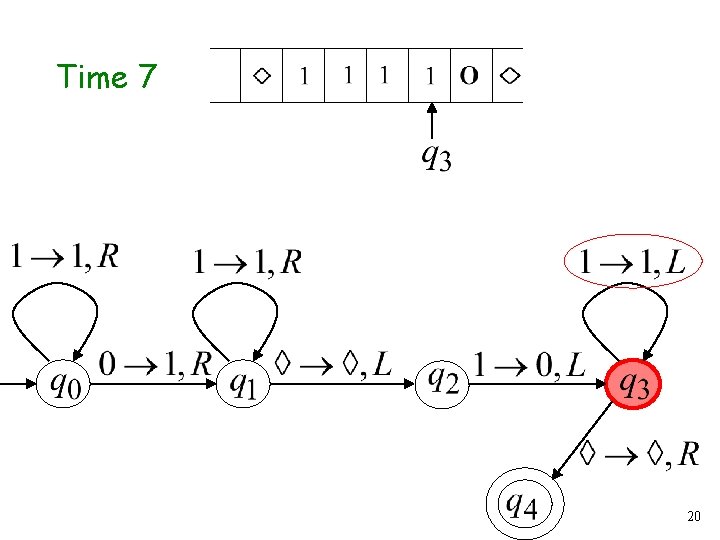
Time 7 20

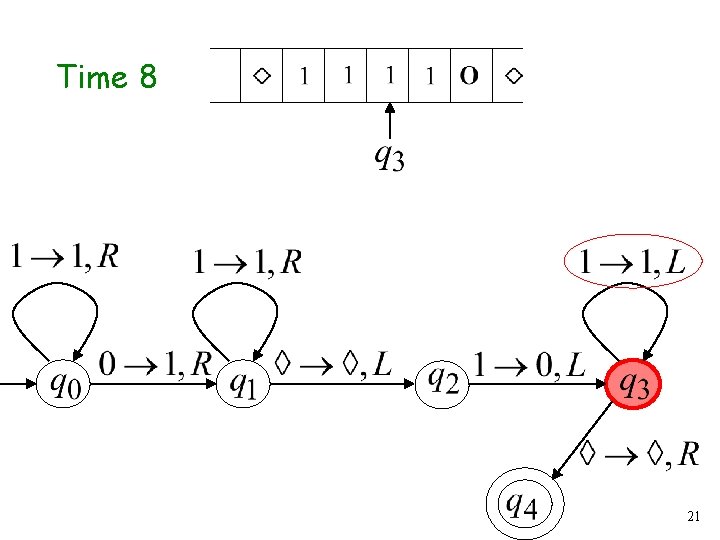
Time 8 21

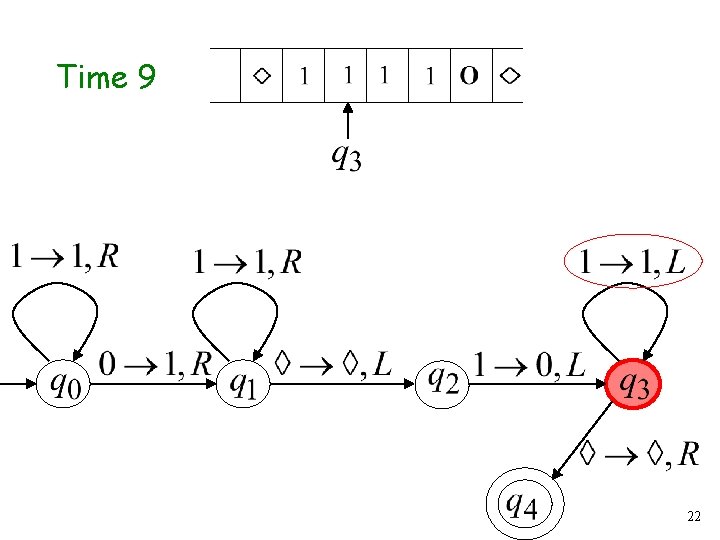
Time 9 22

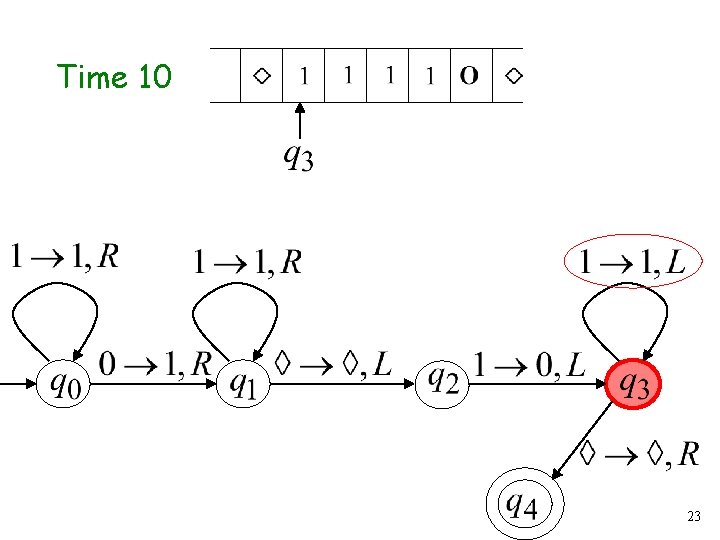
Time 10 23

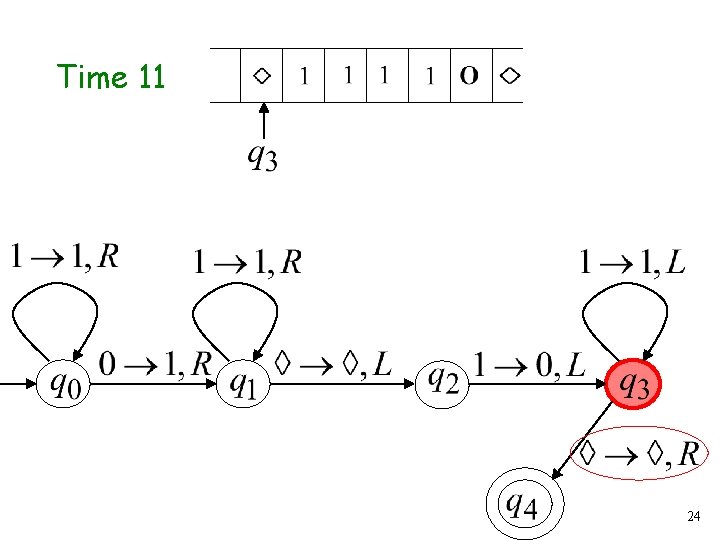
Time 11 24

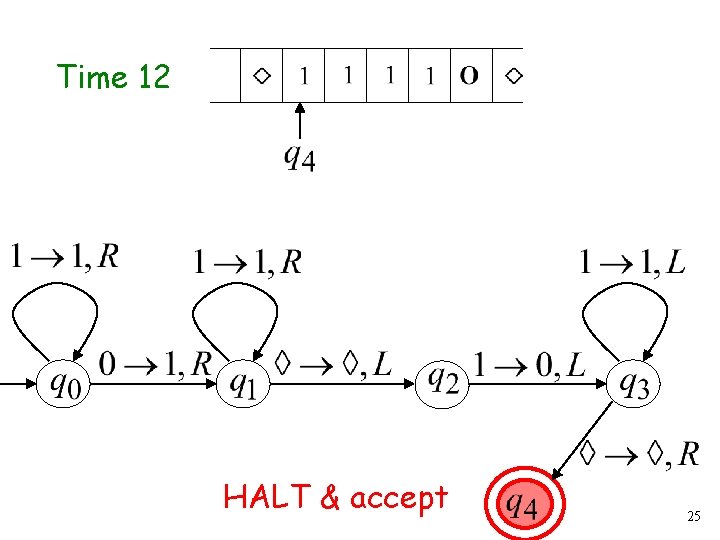
Time 12 HALT & accept 25

Another Example The function is computable is integer Turing Machine: Input string: unary Output string: unary 26

Start initial state Finish final state 27

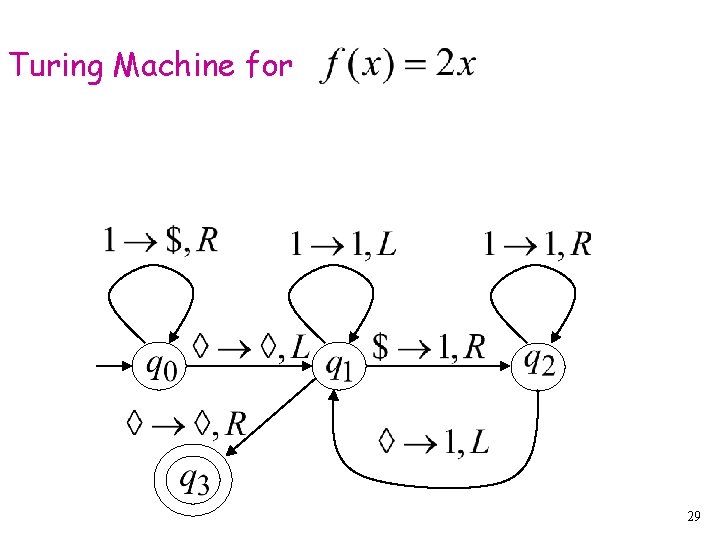
Turing Machine Pseudocode for • Replace every 1 with $ • Repeat: • Find rightmost $, replace it with 1 • Go to right end, insert 1 Until no more $ remain 28

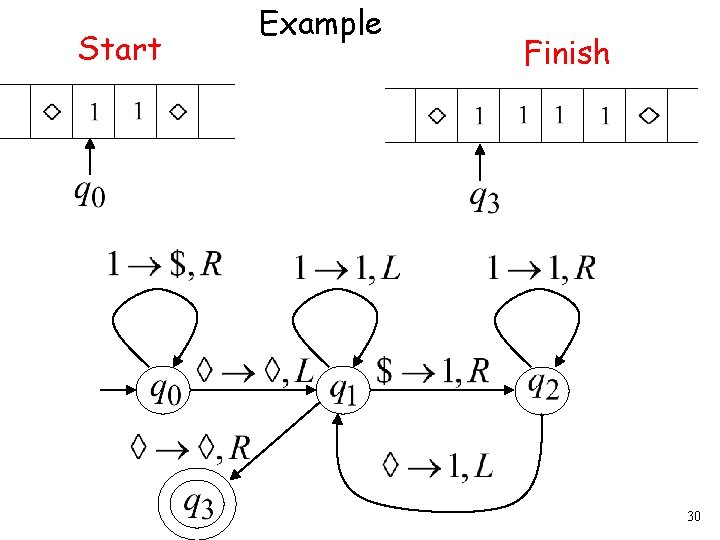
Turing Machine for 29

Start Example Finish 30

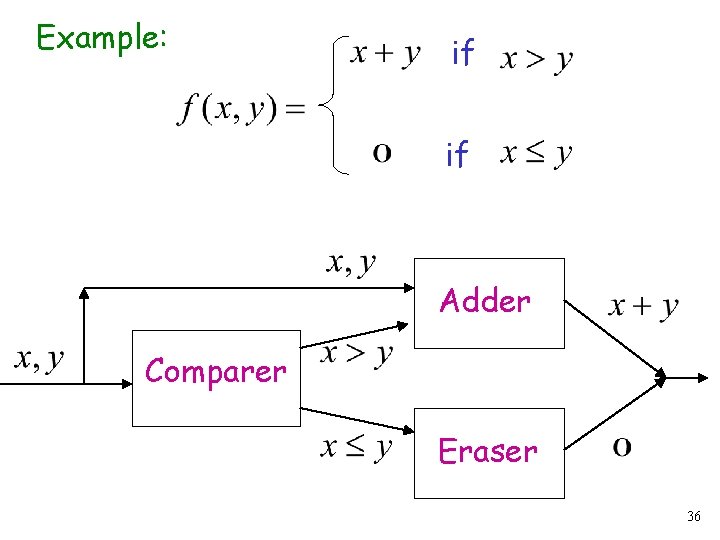
Another Example if The function is computable if 31

Turing Machine for if if Input: Output: or 32

Turing Machine Pseudocode: • Repeat Match a 1 from Until all of or with a 1 from is matched • If a 1 from is not matched erase tape, write 1 else erase tape, write 0 33

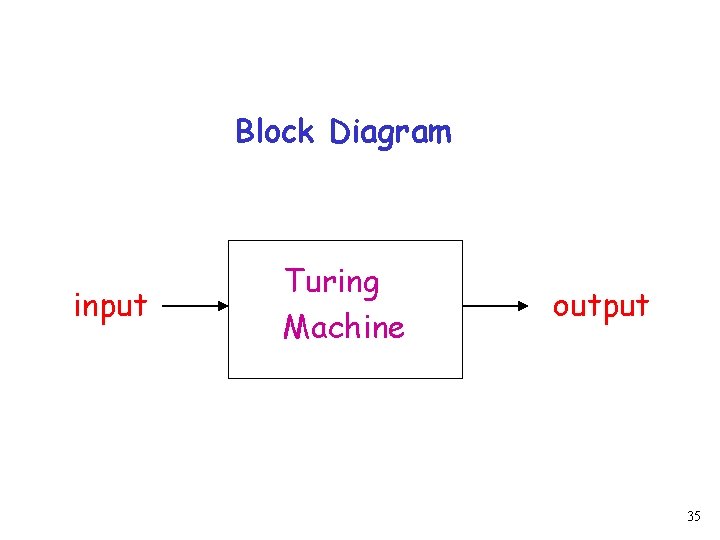
Combining Turing Machines 34

Block Diagram input Turing Machine output 35

Example: if if Adder Comparer Eraser 36

Turing’s Thesis 37

Question: Do Turing machines have the same power with a digital computer? Intuitive answer: Yes There is no formal answer!!! 38

Turing’s thesis: Any computation carried out by mechanical means can be performed by a Turing Machine (1930) 39

Computer Science Law: A computation is mechanical if and only if it can be performed by a Turing Machine There is no known model of computation more powerful than Turing Machines 40

Definition of Algorithm: An algorithm for function is a Turing Machine which computes 41

Algorithms are Turing Machines When we say: There exists an algorithm We mean: There exists a Turing Machine that executes the algorithm 42