Computing degree of determinant via discrete convex optimization

















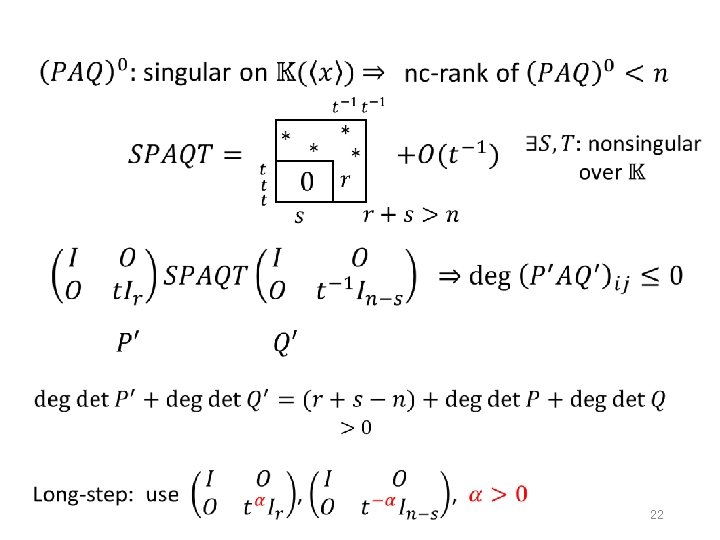

![Thm [Ivanyos et al 2010] Thm [H. 18] weighted ver. mixed polynomial matrix 24 Thm [Ivanyos et al 2010] Thm [H. 18] weighted ver. mixed polynomial matrix 24](https://slidetodoc.com/presentation_image_h2/946463a12f04c793a78773ff8d220f28/image-24.jpg)


![Uniform modular lattice [H. 17] 29 Uniform modular lattice [H. 17] 29](https://slidetodoc.com/presentation_image_h2/946463a12f04c793a78773ff8d220f28/image-29.jpg)





- Slides: 34

Computing degree of determinant via discrete convex optimization over Euclidean building Hiroshi Hirai University of Tokyo hirai@mist. i. u-tokyo. ac. jp Workshop: Recent Development in Optimization 2 GRIPS, Roppongi, Tokyo, 2018/10/13 1

Contents non-commutative combinatorial optimization v. s. linear algebra Submodularity + Discrete convexity 1. Background: Edmonds problem and recent development 2. Motivation + contribution of this work 2

Edmonds Problem Edmonds 1967 3

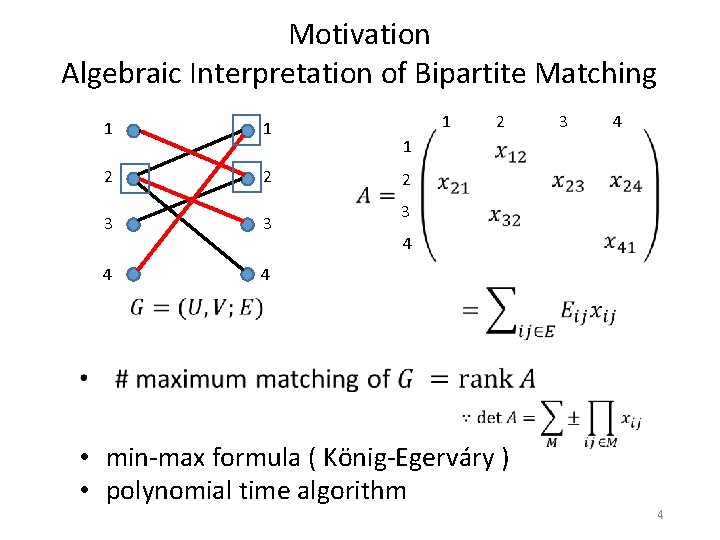
Motivation Algebraic Interpretation of Bipartite Matching 1 1 2 2 3 3 4 4 1 2 3 4 • min-max formula ( König-Egerváry ) • polynomial time algorithm 4

Linear matroid intersection Linear matroid matching ----- Edmonds 1970, Lovász 1981 • Randomized polynomial time algorithm (Lovász 1979) • Connection to circuit complexity (Kabanets-Impagliazzo 2004) 5

Non-commutative Edmonds Problem nc- Ivanyos-Qiao-Subrahmanyam 2015 nc-rank Amitsur 1966 6

7

nc-rank in P !! • Min-max theorem: Fortin-Reutenauer 2004 rank = nc-rank bipartite matching linear matroid intersection s. t. min-max theorem rank < nc-rank non-bipartite matching linear matroid matching 8

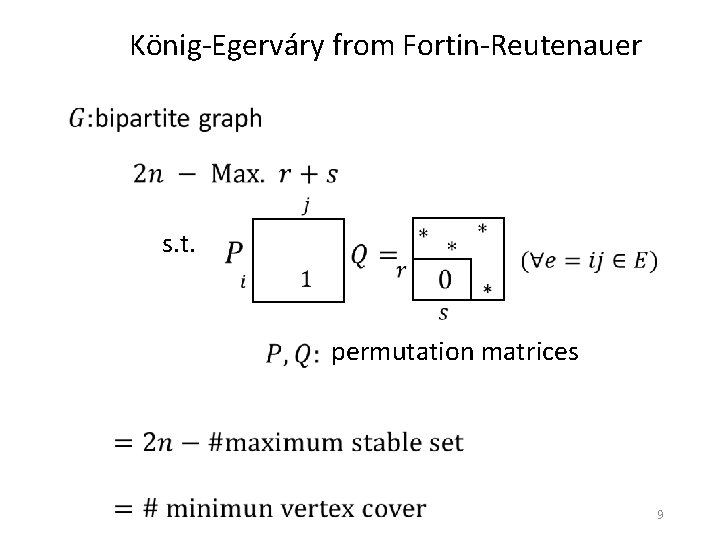
König-Egerváry from Fortin-Reutenauer s. t. permutation matrices 9

Algorithms for nc-rank • Garg-Gurvits-Oliveira-Wigderson 2015 (FOCS’ 16): Gurvits’ operator scaling • Ivanyos-Qiao-Subrahmanyam 2015 (ITCS’ 17): Wong sequence --- vector-space analogue of augmenting path • Hamada-Hirai 2017: Submodularity + convex optimization on CAT(0)-space They are beyond Euclidean convex optimization 10

Submodularity View Hamada-Hirai 2017 s. t. Submodular optimization on the modular lattice of vector subspaces 11

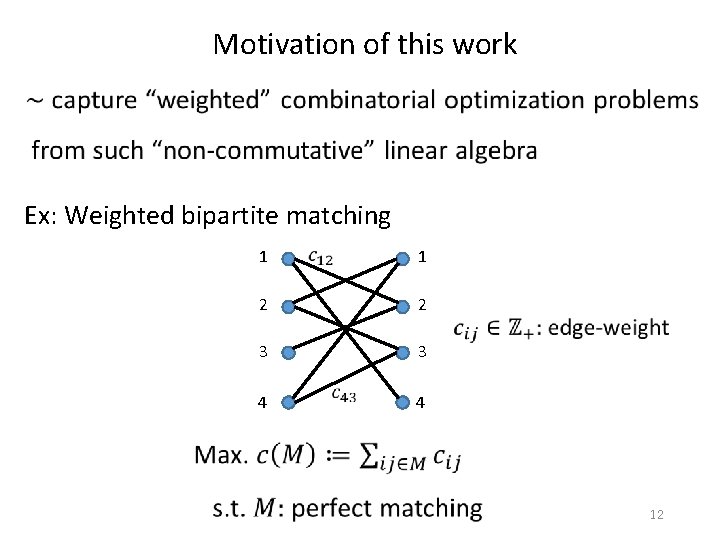
Motivation of this work Ex: Weighted bipartite matching 1 1 2 2 3 3 4 4 12

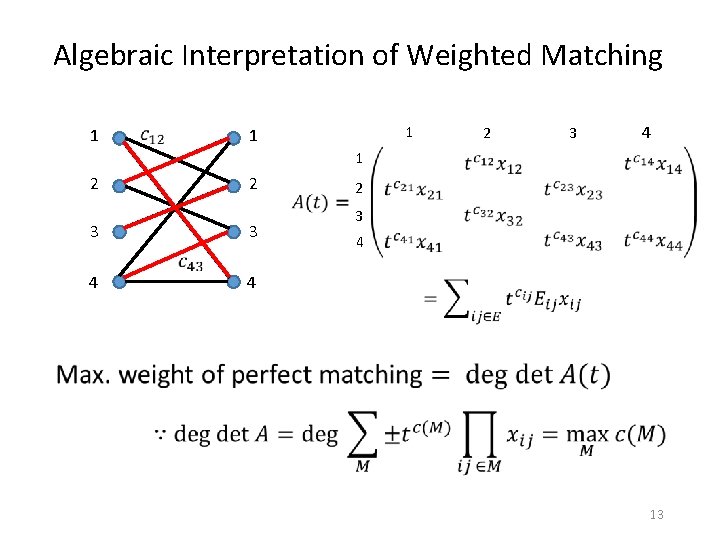
Algebraic Interpretation of Weighted Matching 1 1 1 2 3 4 1 2 2 3 3 4 4 2 3 4 13

Weighted Edmonds Problem Goal: develop a non-commutative version 14

Contribution 15

16

How to define “determinant” of matrices over skew field Bruhat decomposition: LU-decomposition of matrices over skew field uni-lower-triangular uni-upper-triangular diagonal permutation unique commutator group 17

Weighted Non-commutative Edmonds Problem 18

Min-Max Theorem 19

Weak Duality 20

Strong Duality + Algorithm (SDA) 21
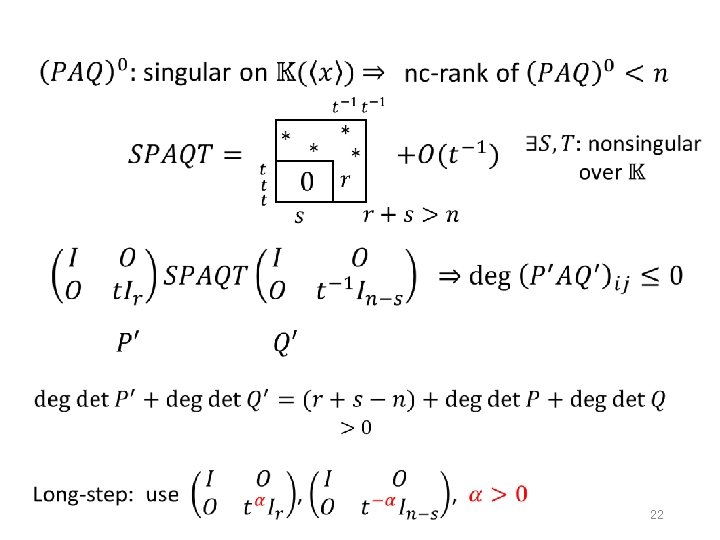
22

Remarks short-step We can improve this bound to 23
![Thm Ivanyos et al 2010 Thm H 18 weighted ver mixed polynomial matrix 24 Thm [Ivanyos et al 2010] Thm [H. 18] weighted ver. mixed polynomial matrix 24](https://slidetodoc.com/presentation_image_h2/946463a12f04c793a78773ff8d220f28/image-24.jpg)
Thm [Ivanyos et al 2010] Thm [H. 18] weighted ver. mixed polynomial matrix 24

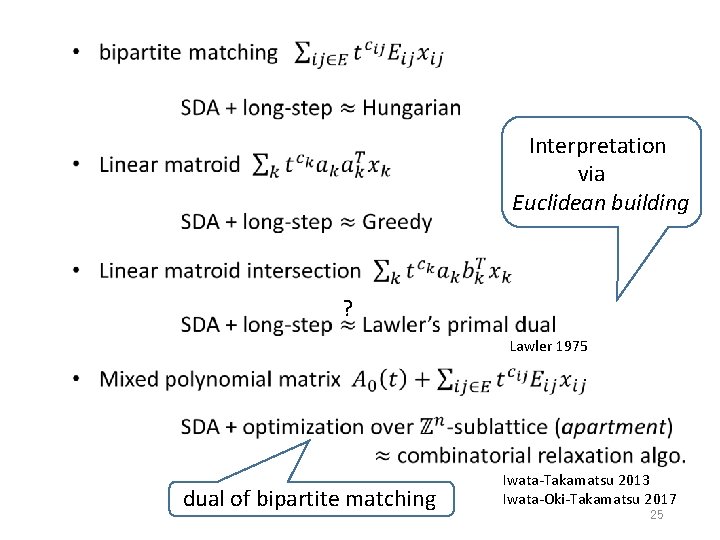
Interpretation via Euclidean building ? Lawler 1975 dual of bipartite matching Iwata-Takamatsu 2013 Iwata-Oki-Takamatsu 2017 25

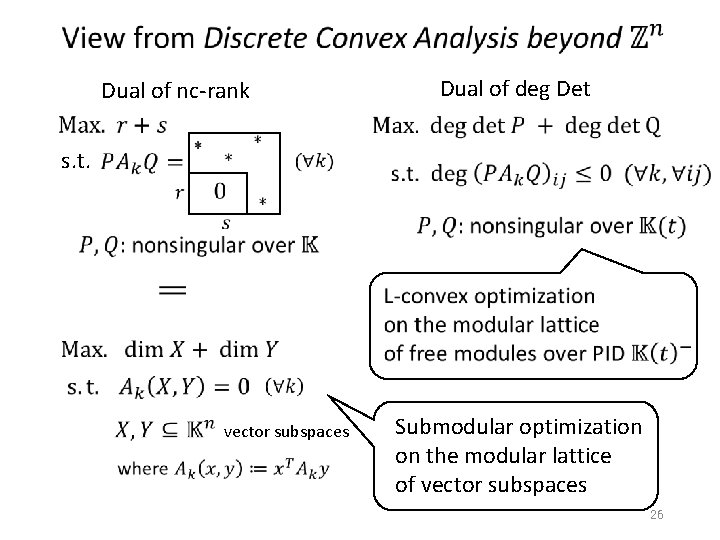
Dual of nc-rank Dual of deg Det s. t. vector subspaces Submodular optimization on the modular lattice of vector subspaces 26

27

28
![Uniform modular lattice H 17 29 Uniform modular lattice [H. 17] 29](https://slidetodoc.com/presentation_image_h2/946463a12f04c793a78773ff8d220f28/image-29.jpg)
Uniform modular lattice [H. 17] 29

L-convexity on uniform modular lattice Several DCA concepts/properties are naturally extended 30

is viewed as L-convex function minimization on uniform modular lattice • SDA = steepest descent algorithm for this L-convex function: submodular optimization adapting Murota-Shioura 2014 31

Summary • Edmonds problem, rank v. s. nc-rank • Weighted Edmonds problem, deg det v. s. deg Det formulation, algorithm, special case of deg det = deg Det • Submodularity / discrete convexity aspect L-convexity on uniform modular lattice (= Euclidean building) 32

Problems • Representable by deg det but deg det < deg Det : Non-bipartite matching: Edmonds 1965 Matching forest: Giles 1982 Path matching: Cunningham-Geelen 1997 Linear matroid matching: Lovász 1980, Iwata-Kobayashi 2017 Can we develop a unified theory ? 33

References H. Hirai: Uniform modular lattice and Euclidean building, 2017 H. Hirai: Uniform semimodular lattice and valuated matroid, 2018 H. Hirai: Computing degree of determinant via discrete convex optimization over Euclidean building, 2018. Thank you for your attention 34