Computing Beyond CMOS Intense research into novel materials

Computing Beyond CMOS Intense research into novel materials and devices: Carbon Nanotubes… Biological Processes… Molecular Switches… 5/31/07 IWLS 2007 1

Computing Beyond CMOS Many technologies still in exploratory phase: c ! 5/31/07 IWLS 2007 2

Nanoscale Circuits Identify general traits that impinge upon logic synthesis: Features: • High density of bits. Challenges: • Topological constraints. • Inherent randomness. • High defect rates. carbon nanowire crossbar 5/31/07 IWLS 2007 3

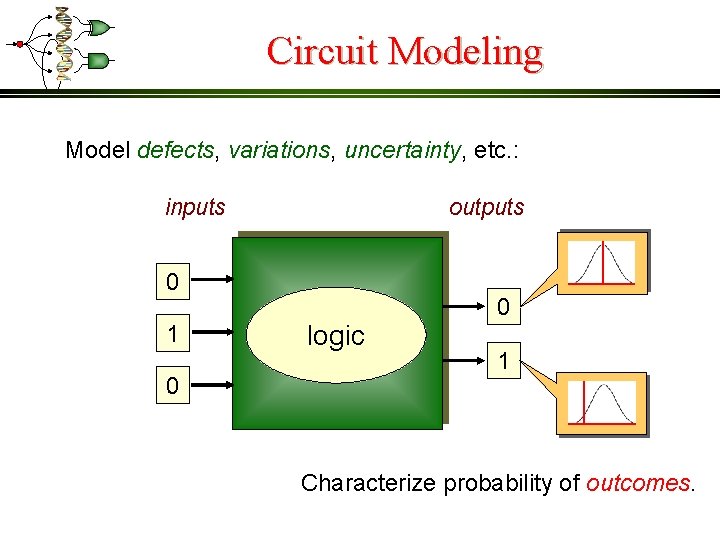
Circuit Modeling Model defects, variations, uncertainty, etc. : inputs outputs 0 1 0 logic 0 1 Characterize probability of outcomes.

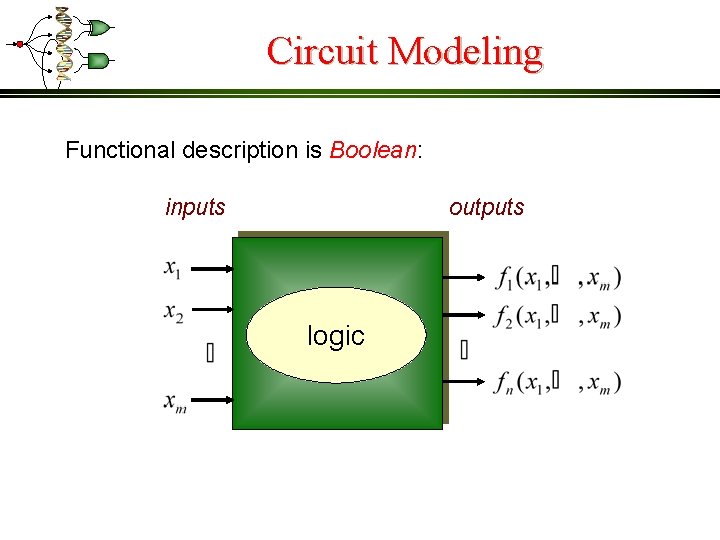
Circuit Modeling Functional description is Boolean: inputs outputs logic

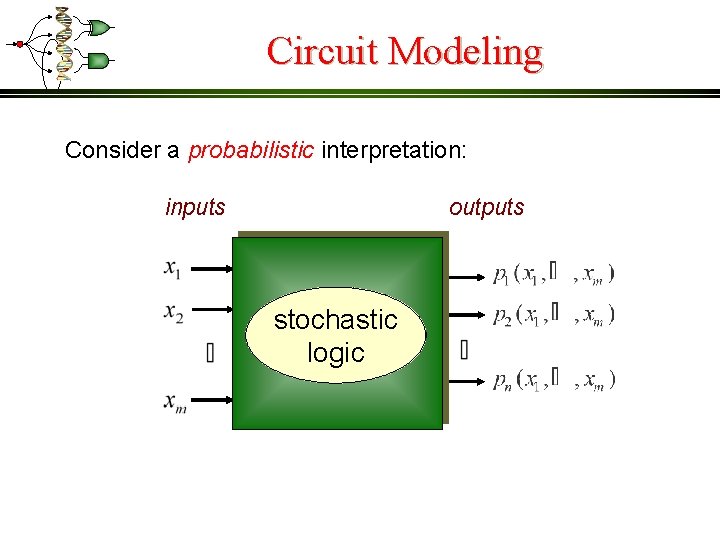
Circuit Modeling Consider a probabilistic interpretation: inputs outputs stochastic logic

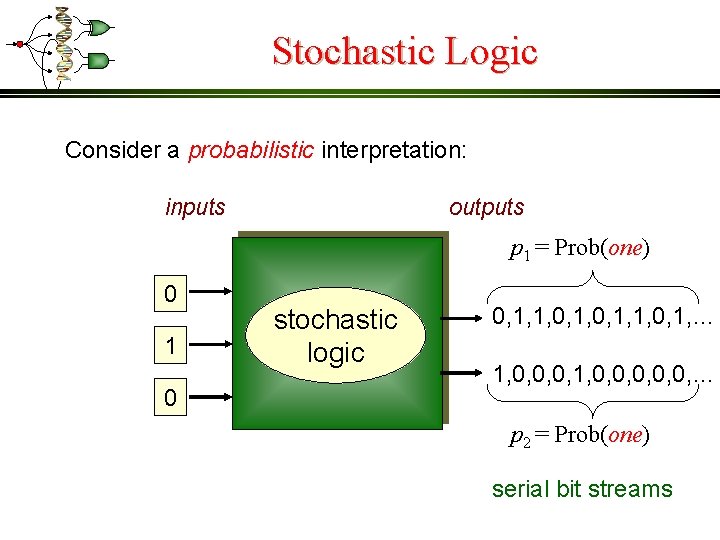
Stochastic Logic Consider a probabilistic interpretation: inputs outputs p 1 = Prob(one) 0 1 0 stochastic logic 0, 1, 1, 0, 1, … 1, 0, 0, 0, … p 2 = Prob(one) serial bit streams

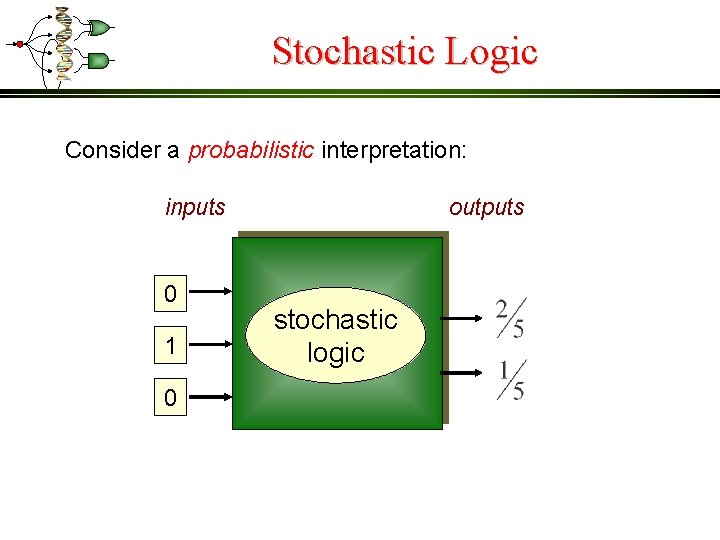
Stochastic Logic Consider a probabilistic interpretation: inputs 0 1 0 outputs stochastic logic

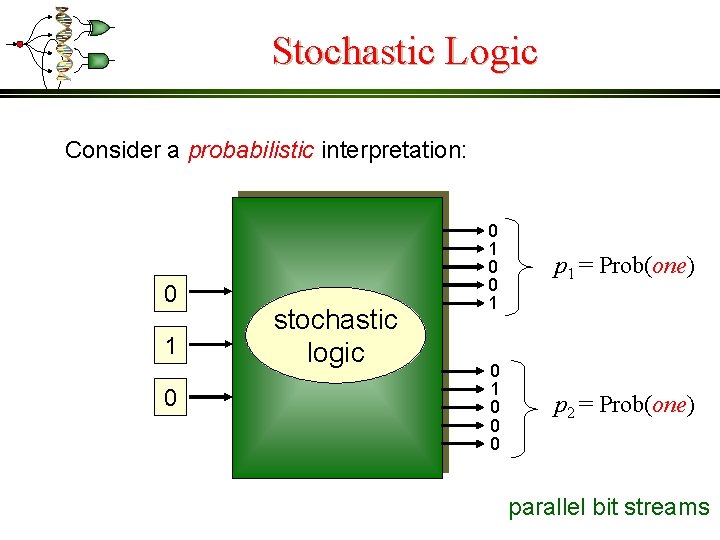
Stochastic Logic Consider a probabilistic interpretation: 0 1 0 stochastic logic 0 1 0 0 1 p 1 = Prob(one) 0 1 0 0 0 p 2 = Prob(one) parallel bit streams

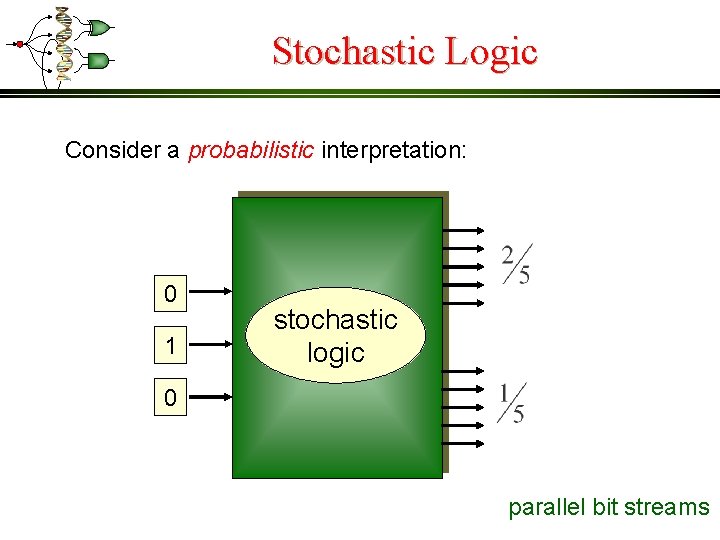
Stochastic Logic Consider a probabilistic interpretation: 0 1 stochastic logic 0 parallel bit streams

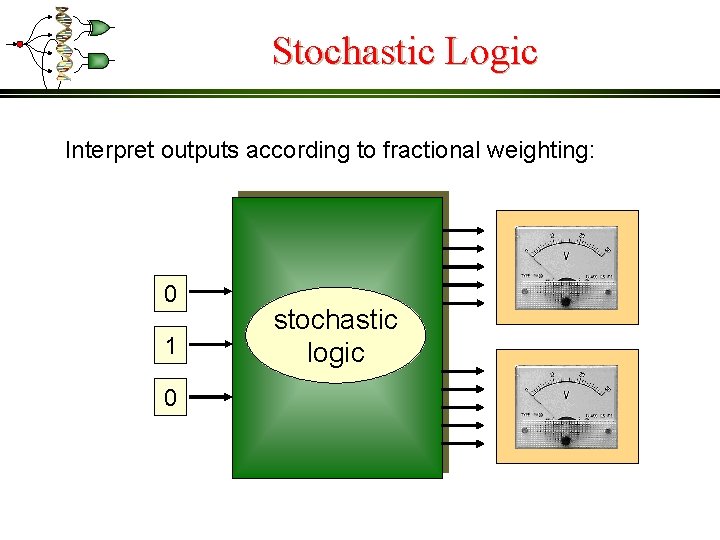
Stochastic Logic Interpret outputs according to fractional weighting: 0 1 0 stochastic logic

Synthesis of Stochastic Logic Given a technology characterized by: • High degree of structural parallelism. • Inherent randomness in logic/interconnects. Synthesize: • Circuit that computes a probability distribution corresponding to a logical specification. Strategy: • Cast problem in terms of arithmetic operations. • Perform synthesis with binary moment diagrams. 5/31/07 IWLS 2007 12

Probabilistic Bundles 0 1 0 0 1 X x A real value x in [0, 1] is encoded as a stream of bits X. For each bit, the probability that it is one is: P(X=1) = x. 5/31/07 IWLS 2007 13

Arithmetic Operations Multiplication (Scaled) Addition c = P(C ) = P( A) P( B ) c = P(C ) = P( S ) P( A) +[1 - P( S )]P( B) = s a + (1 - s ) b =ab 5/31/07 IWLS 2007 14

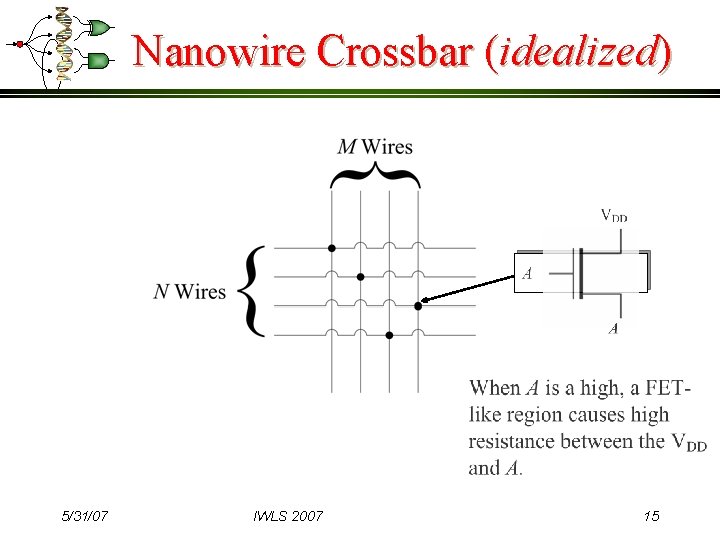
Nanowire Crossbar (idealized) 5/31/07 IWLS 2007 15

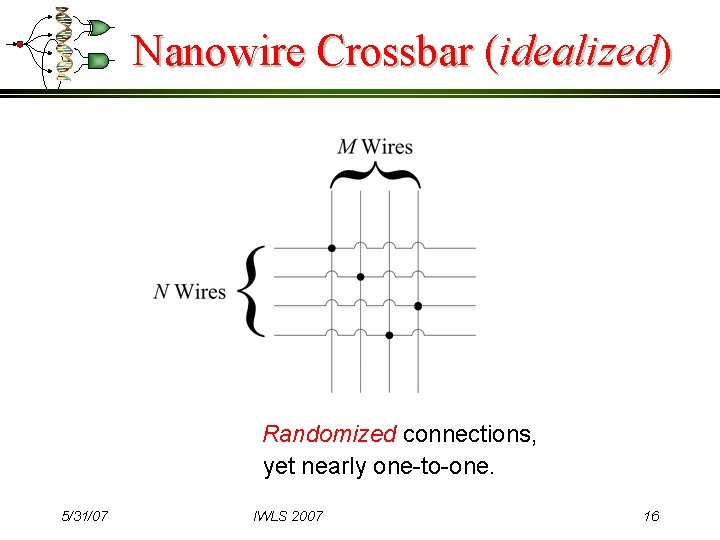
Nanowire Crossbar (idealized) Randomized connections, yet nearly one-to-one. 5/31/07 IWLS 2007 16

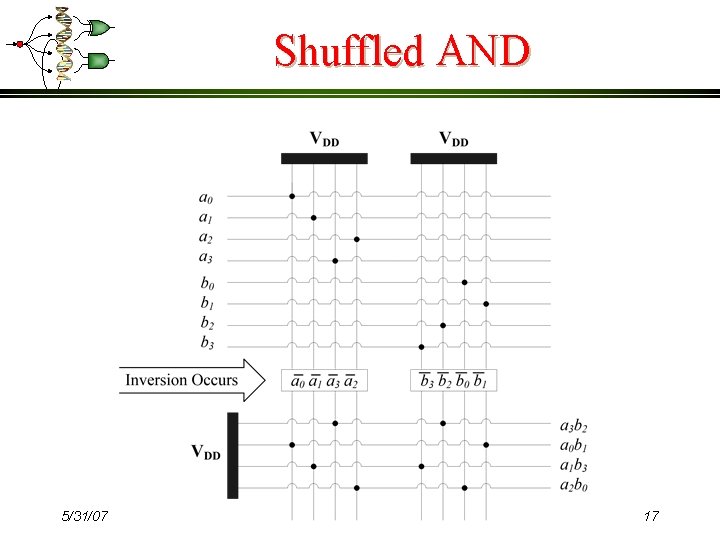
Shuffled AND 5/31/07 17

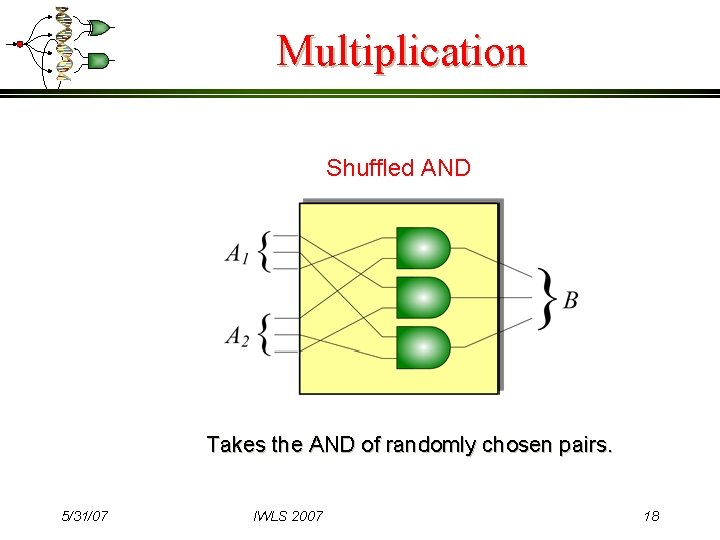
Multiplication Shuffled AND Takes the AND of randomly chosen pairs. 5/31/07 IWLS 2007 18

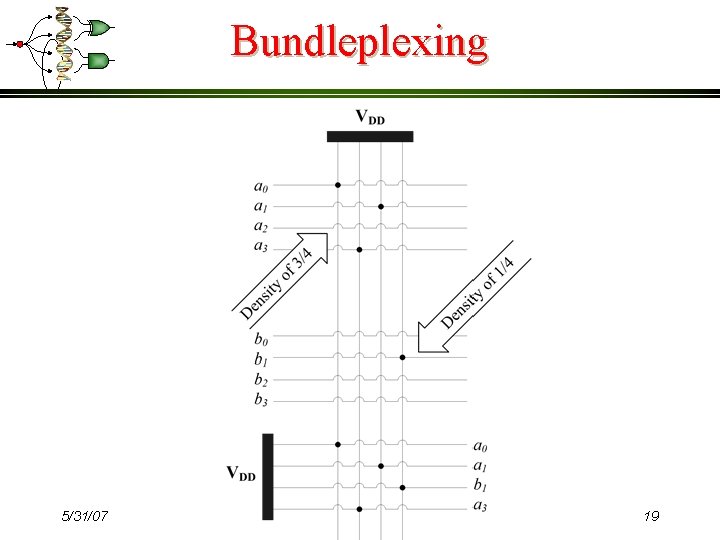
Bundleplexing 5/31/07 19

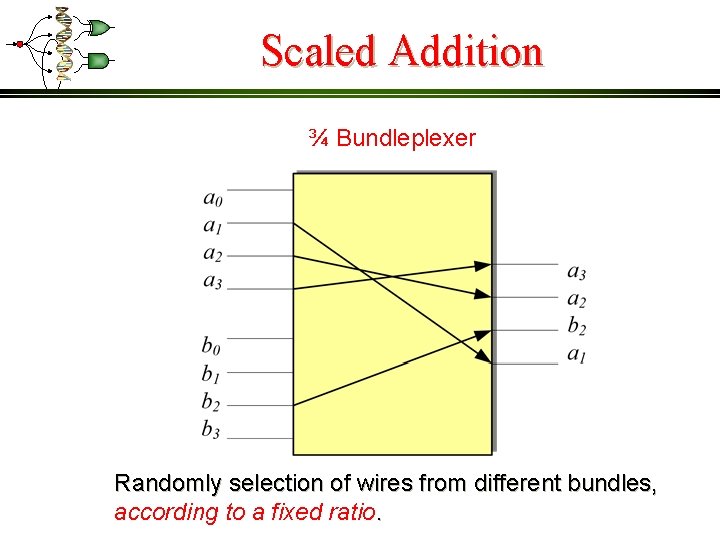
Scaled Addition ¾ Bundleplexer Randomly selection of wires from different bundles, according to a fixed ratio.

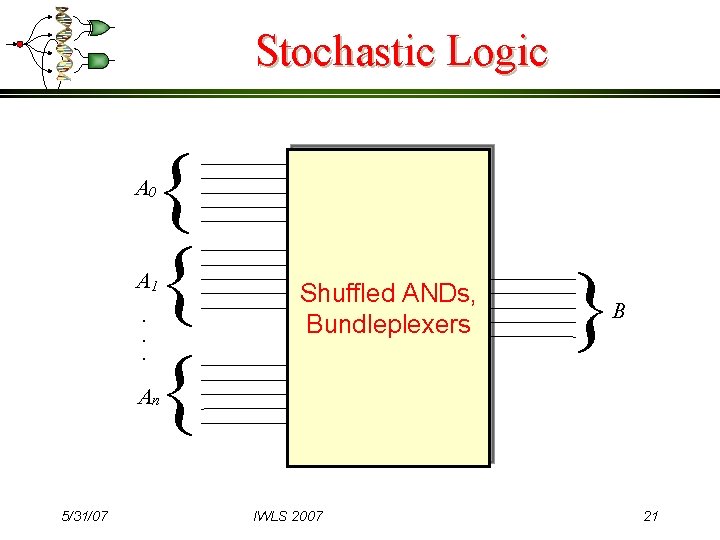
Stochastic Logic { { { A 0 A 1. . . Shuffled ANDs, Bundleplexers } B An 5/31/07 IWLS 2007 21

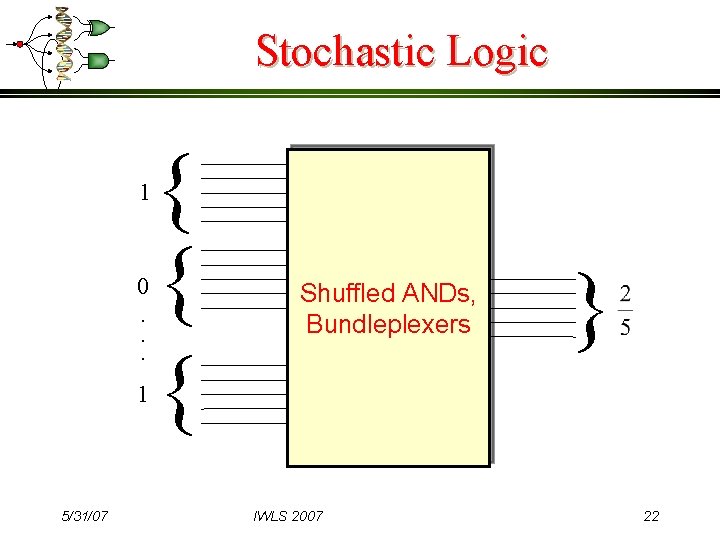
Stochastic Logic 1 0. . . 1 5/31/07 { { { Shuffled ANDs, Bundleplexers IWLS 2007 } 22