Computing and Interpreting Appropriate Confidence Intervals Prof Catherine

Computing and Interpreting Appropriate Confidence Intervals Prof Catherine Comiskey School of Nursing and Midwifery 24 D'Olier Street Dublin 2

Overview n n n Computing a confidence interval (CI) for a sample mean (average) when the population standard deviation (sigma) is known Using the t distribution and computing CI for a sample mean when the population standard deviation is unknown Computing a CI for a sample proportion. School of Nursing and Midwifery 24 D'Olier Street Dublin 2

Confidence Intervals and Hypothesis Tests n Estimating Confidence Intervals, CI n Means and Proportions n Examples and Exercises © 2007 Thomson South-Western. All Rights Reserved Slide 3

Margin of Error and the Interval Estimate A point estimator cannot be expected to provide the exact value of the population parameter. An interval estimate can be computed by adding and subtracting a margin of error to the point estimate. Point Estimate +/- Margin of Error The purpose of an interval estimate is to provide information about how close the point estimate is to the value of the parameter. © 2007 Thomson South-Western. All Rights Reserved Slide 4

Margin of Error and the Interval Estimate The general form of an interval estimate of a population mean is © 2007 Thomson South-Western. All Rights Reserved Slide 5

Interval Estimation of a Population Mean: Known n In order to develop an interval estimate of a population mean, the margin of error must be computed using either: • the population standard deviation , or • the sample standard deviation s is rarely known exactly, but often a good estimate can be obtained based on historical data or other information. We refer to such cases as the known case. © 2007 Thomson South-Western. All Rights Reserved Slide 6

Interval Estimate of a Population Mean: Known (key slide) n Interval Estimate of where: 1 - z /2 n is the sample mean is the confidence coefficient is the z value providing an area of /2 in the upper tail of the standard normal probability distribution is the population standard deviation is the sample size © 2007 Thomson South-Western. All Rights Reserved Slide 7

Interval Estimate of a Population Mean: Known n Adequate Sample Size In most applications, a sample size of n = 30 is adequate. If the population distribution is highly skewed or contains outliers, a sample size of 50 or more is recommended. © 2007 Thomson South-Western. All Rights Reserved Slide 8

Interval Estimate of a Population Mean: Known n Adequate Sample Size (continued) If the population is not normally distributed but is roughly symmetric, a sample size as small as 15 will suffice. If the population is believed to be at least approximately normal, a sample size of less than 15 can be used. © 2007 Thomson South-Western. All Rights Reserved Slide 9

Interval Estimate of Population Mean: Known Example: Discount Sounds has 260 retail outlets throughout the country. The firm is evaluating a potential location for a new outlet, based in part, on the mean annual income of the individuals in the marketing area of the new location. A sample of size n = 36 was taken; the sample mean income was € 31, 100. The population is not believed to be highly skewed. The population standard deviation is estimated to be € 4, 500, and the confidence coefficient to be used in the interval estimate is. 95. n D © 2007 Thomson South-Western. All Rights Reserved S Slide 10

Interval Estimate of Population Mean: Known (key slide) 95% of the sample means that can be observed are within + 1. 96 of the population mean . D S The margin of error is: Thus, at 95% confidence, the margin of error is € 1, 470. © 2007 Thomson South-Western. All Rights Reserved Slide 11

Interval Estimate of Population Mean: Known (key slide) D S Interval estimate of is: € 31, 100 + € 1, 470 or € 29, 630 to € 32, 570 We are 95% confident that the interval contains the population mean. © 2007 Thomson South-Western. All Rights Reserved Slide 12

Class Exercise 1 During a work health and safety week a random sample of 55 employees had their blood pressure recorded. Results in mm of Hg gave a sample mean 102. 4. It is known that individuals with the same age distribution as the employees have a blood pressure standard deviation of 10. 5 mm. Compute a 95% CI for the mean blood pressure of the population of employees. © 2007 Thomson South-Western. All Rights Reserved Slide 13

Interval Estimation of a Population Mean: Unknown n n If an estimate of the population standard deviation cannot be developed prior to sampling, we use the sample standard deviation s to estimate . This is the unknown case. In this case, the interval estimate for is based on the t distribution. (We’ll assume for now that the population is normally distributed. ) © 2007 Thomson South-Western. All Rights Reserved Slide 14

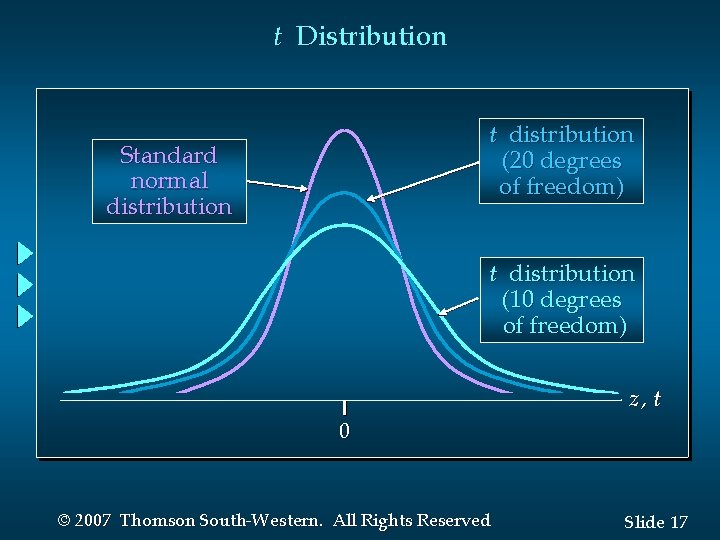
t Distribution The t distribution is a family of similar probability distributions. A specific t distribution depends on a parameter known as the degrees of freedom. Degrees of freedom refer to the number of independent pieces of information that go into the computation of s. © 2007 Thomson South-Western. All Rights Reserved Slide 15

t Distribution A t distribution with more degrees of freedom has less dispersion. As the number of degrees of freedom increases, the difference between the t distribution and the standard normal probability distribution becomes smaller and smaller. © 2007 Thomson South-Western. All Rights Reserved Slide 16

t Distribution t distribution (20 degrees of freedom) Standard normal distribution t distribution (10 degrees of freedom) z, t 0 © 2007 Thomson South-Western. All Rights Reserved Slide 17

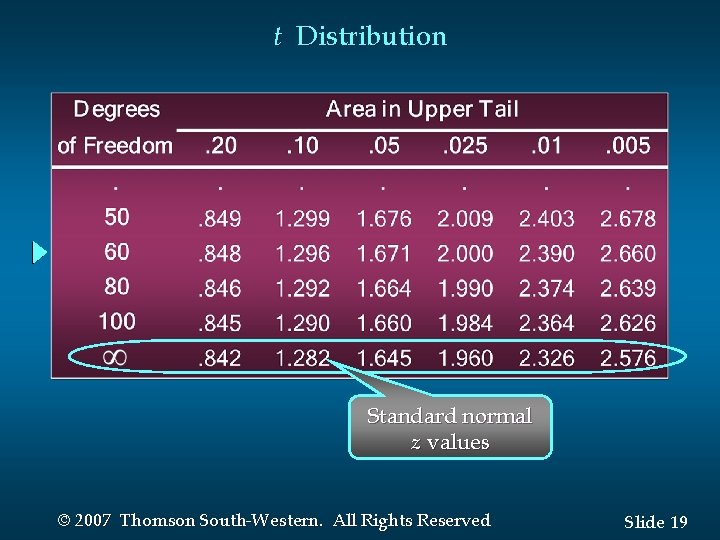
t Distribution For more than 100 degrees of freedom, the standard normal z value provides a good approximation to the t value. The standard normal z values can be found in the infinite degrees ( ) row of the t distribution table. © 2007 Thomson South-Western. All Rights Reserved Slide 18

t Distribution Standard normal z values © 2007 Thomson South-Western. All Rights Reserved Slide 19

Interval Estimation of a Population Mean: Unknown (key slide) n Interval Estimate where: 1 - = the confidence coefficient t /2 = the t value providing an area of /2 in the upper tail of a t distribution with n - 1 degrees of freedom s = the sample standard deviation © 2007 Thomson South-Western. All Rights Reserved Slide 20

Interval Estimation of a Population Mean: Unknown n Example: Family Rents A reporter for a regional newspaper is writing an article on the cost of family housing. A sample of 16 apartments within a half-mile of the town centre resulted in a sample mean of € 650 per month and a sample standard deviation of € 55. © 2007 Thomson South-Western. All Rights Reserved Slide 21

Interval Estimation of a Population Mean: Unknown n Example: Family Rents Let us provide a 95% confidence interval estimate of the mean rent per month for the population of apartments within a half-mile of town. We will assume this population to be normally distributed. © 2007 Thomson South-Western. All Rights Reserved Slide 22

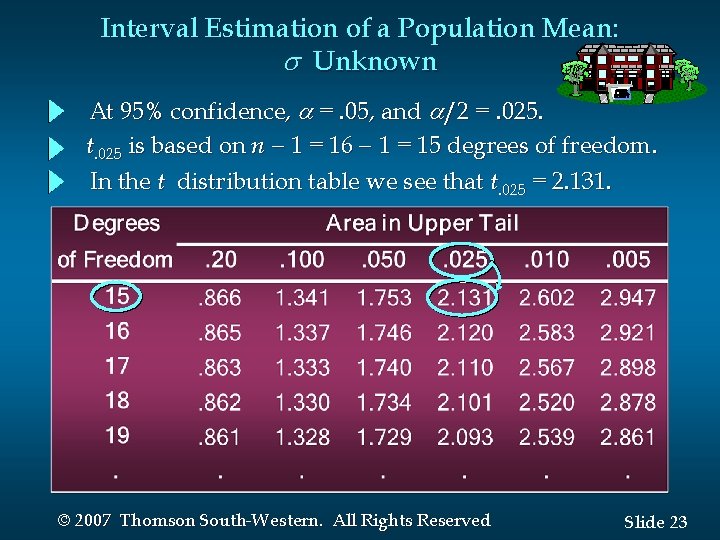
Interval Estimation of a Population Mean: Unknown At 95% confidence, =. 05, and /2 =. 025. t. 025 is based on n - 1 = 16 - 1 = 15 degrees of freedom. In the t distribution table we see that t. 025 = 2. 131. © 2007 Thomson South-Western. All Rights Reserved Slide 23

Interval Estimation of a Population Mean: Unknown (key slide) n Interval Estimate Margin of Error We are 95% confident that the mean rent per month for the population of family apartments within a half-mile of town is between € 620. 70 and € 679. 30. © 2007 Thomson South-Western. All Rights Reserved Slide 24

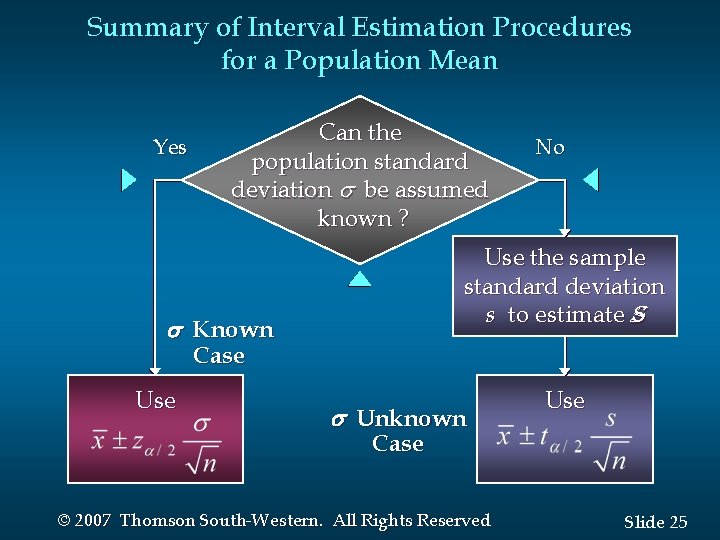
Summary of Interval Estimation Procedures for a Population Mean Yes Can the population standard deviation be assumed known ? No Use the sample standard deviation s to estimate s s Known Case Use s Unknown Use Case © 2007 Thomson South-Western. All Rights Reserved Slide 25

Interval Estimation of a Population Proportion The general form of an interval estimate of a population proportion is © 2007 Thomson South-Western. All Rights Reserved Slide 26

Interval Estimation of a Population Proportion The sampling distribution of plays a key role in computing the margin of error for this interval estimate. The sampling distribution of can be approximated by a normal distribution whenever np > 5 and n(1 – p ) > 5. © 2007 Thomson South-Western. All Rights Reserved Slide 27

Interval Estimation of a Population Proportion n Interval Estimate where: 1 - is the confidence coefficient z /2 is the z value providing an area of /2 in the upper tail of the standard normal probability distribution is the sample proportion © 2007 Thomson South-Western. All Rights Reserved Slide 28

Example Barron, Comiskey and Saris (2009) BMI in 900 Irish children n © 2007 Thomson South-Western. All Rights Reserved Slide 29