Computeraided Selection of Test Models for Model Transformation

Computer-aided Selection of Test Models for Model Transformation Testing Sagar Sen Benoit Baudry IRISA/INRIA Campus Universitaire de Beaulieu, Rennes 35000, France

Outline What is a Model Transformation ? Why is it important to Test Transformations ? Overview of the Transformation Testing Framework What are the Challenges involved? What is Test Model Selection in the Testing? Solution to Test Model Selection Problem Conclusion

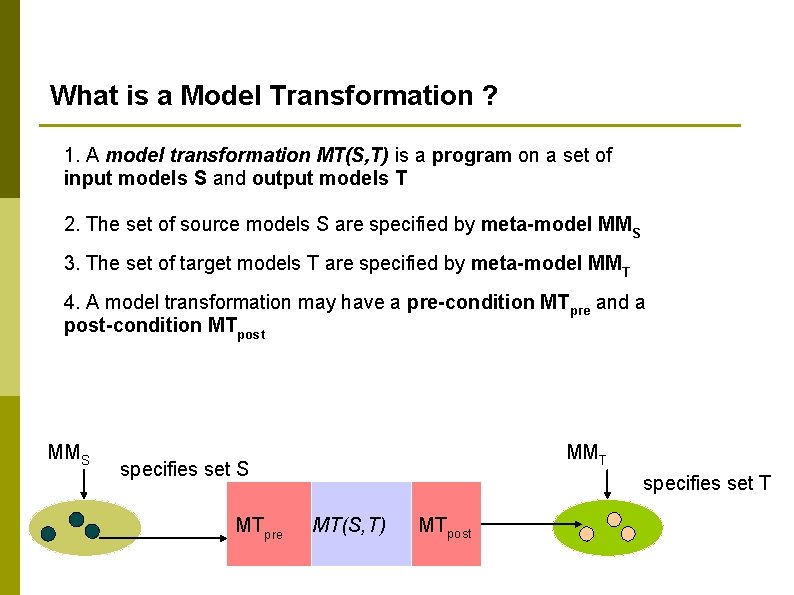
What is a Model Transformation ? 1. A model transformation MT(S, T) is a program on a set of input models S and output models T 2. The set of source models S are specified by meta-model MMS 3. The set of target models T are specified by meta-model MMT 4. A model transformation may have a pre-condition MTpre and a post-condition MTpost MMS MMT specifies set S MTpre specifies set T MT(S, T) MTpost

Applications of Model Transformations 1. Model transformation pipelines such as XML to XML Pipelines (Eg: Xproc) 2. Code Generators (Eg: Simulink Model to Code) 3. UML Class Diagram serialization to RDBMS (Eg: Hibernate 3. 0) 4. Simulation Traces (Eg: Simulink, Modelica) 5. UML Model Design Re-factoring (Eg: Rhapsody) 7. Code migration (Cobol to Java/C#, VPLUS UI to XML/J 2 EE ) 8. Game development pipelines (Eg: XNA Studio) 9. Business Process Models (Eg: Websphere business process model) 10. Code reverse engineering. . .

Why test model transformations ? Motivation A Typical Model-driven Development Process Model

Why test model transformations ? Motivation A Typical Model-driven Development Process Model Composition

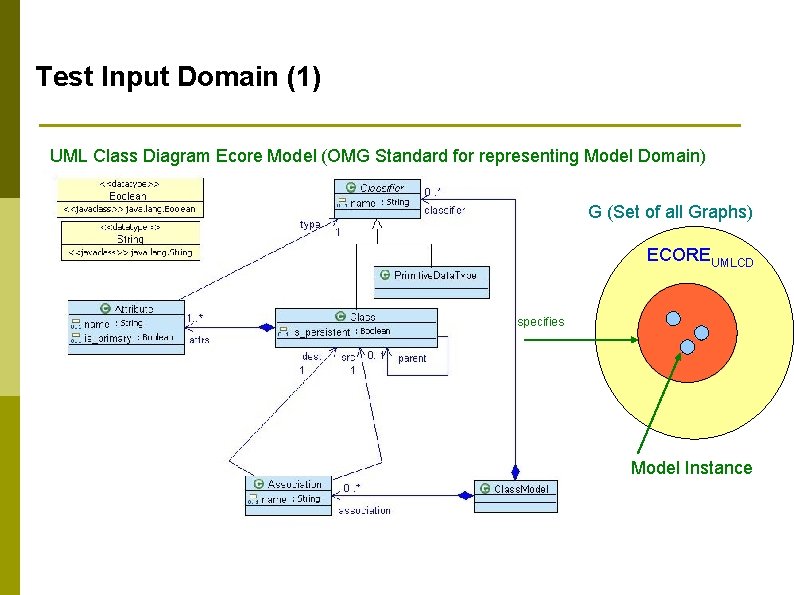
Test Input Domain (1) UML Class Diagram Ecore Model (OMG Standard for representing Model Domain) G (Set of all Graphs) ECOREUMLCD specifies Model Instance

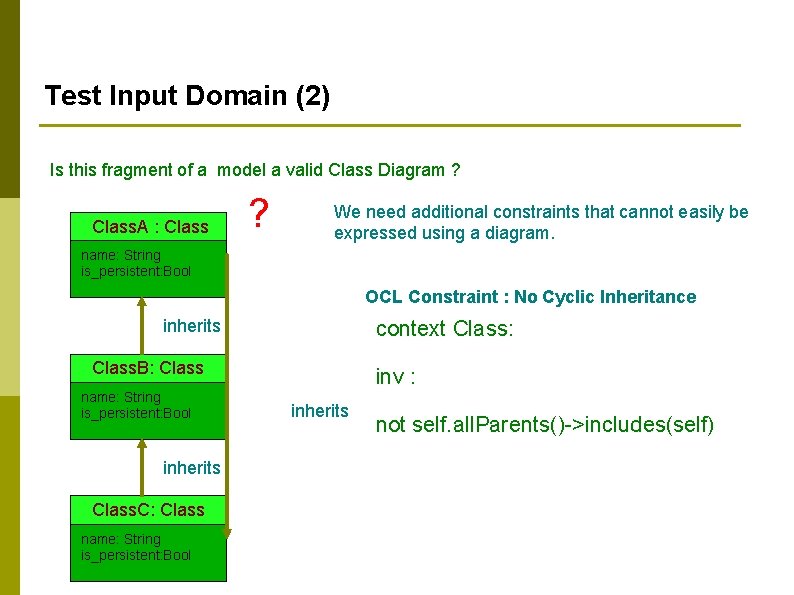
Test Input Domain (2) Is this fragment of a model a valid Class Diagram ? Class. A : Class ? We need additional constraints that cannot easily be expressed using a diagram. name: String is_persistent: Bool OCL Constraint : No Cyclic Inheritance inherits context Class: Class. B: Class name: String is_persistent: Bool inherits Class. C: Class name: String is_persistent: Bool inv : inherits not self. all. Parents()->includes(self)

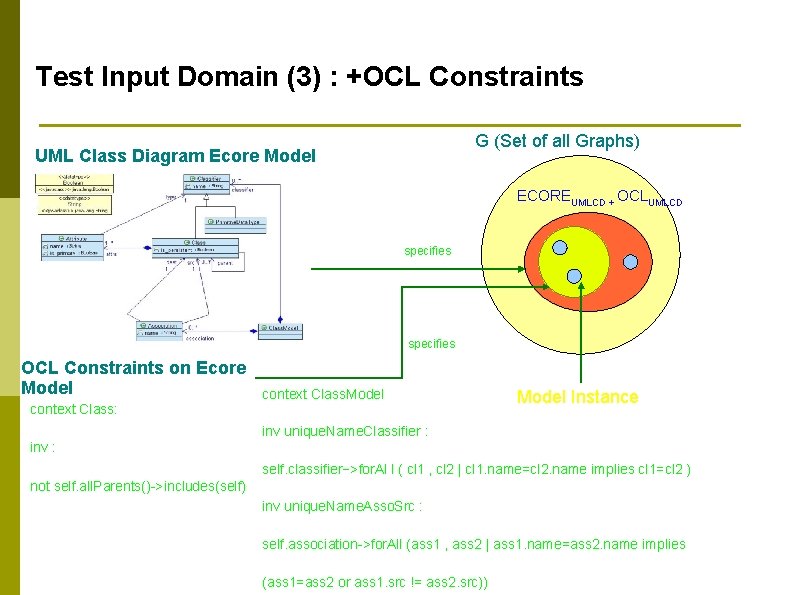
Test Input Domain (3) : +OCL Constraints G (Set of all Graphs) UML Class Diagram Ecore Model ECOREUMLCD + OCLUMLCD specifies OCL Constraints on Ecore Model context Class: context Class. Model Instance inv unique. Name. Classifier : inv : self. classifier−>for. Al l ( cl 1 , cl 2 | cl 1. name=cl 2. name implies cl 1=cl 2 ) not self. all. Parents()->includes(self) inv unique. Name. Asso. Src : self. association->for. All (ass 1 , ass 2 | ass 1. name=ass 2. name implies (ass 1=ass 2 or ass 1. src != ass 2. src))

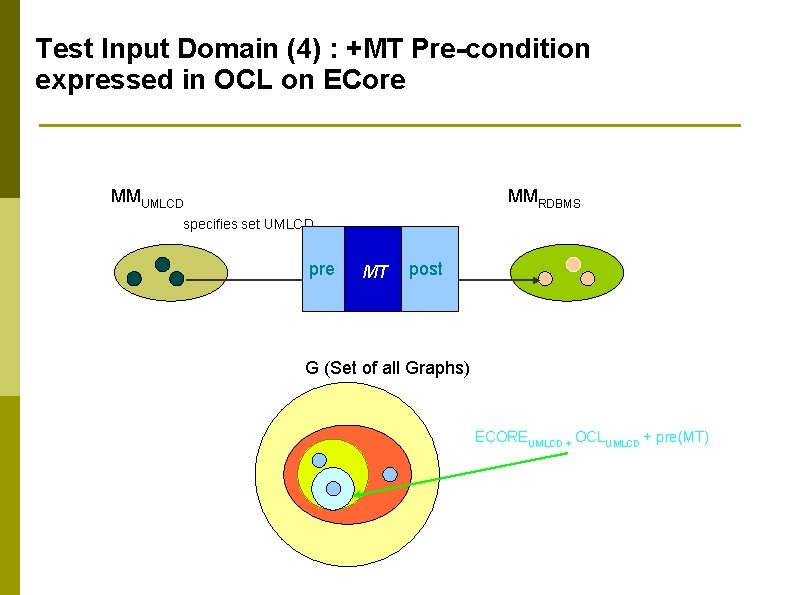
Test Input Domain (4) : +MT Pre-condition expressed in OCL on ECore MMUMLCD MMRDBMS specifies set UMLCD pre MT post G (Set of all Graphs) ECOREUMLCD + OCLUMLCD + pre(MT) specifies

Test Input Domain (5) + Testers Requirements 1. Partitions on input domain based on Partitioning Criteria : Category Partitioning 2. Number of objects of a particular type 3. Partial model Instance 4. Mutation analysis score based on output of model transformation 5. Satisfaction of post-condition G (Set of all Graphs) ECOREUMLCD + OCLUMLCD + pre(MT)+Requirements specifies Test Input Domain+ Constraints =Test Model Knowledge

Test Model Knowledge 1. A set of model fragments (partition on the input domain) as sets of constraints or partial instances 2. A set of model requirements expressed as constraints on the metamodel 3. The model transformation pre-condition MTpre Constraints on context MM S Object instances of MM S expressed as Partial Instance ECore+OCL expressed as Pre-condition expressed as Requirements Common Constraint Language Meta-model expressed as Constraints on context MM S Or Object instances as +ve or –ve application conditions 1. 2. 3. 4. Analyzable: Do the constraints conflict? Test Model Instance Generation Sufficiently expressive (first-order logic and beyond) Large libraries of predefined constraints New test direction

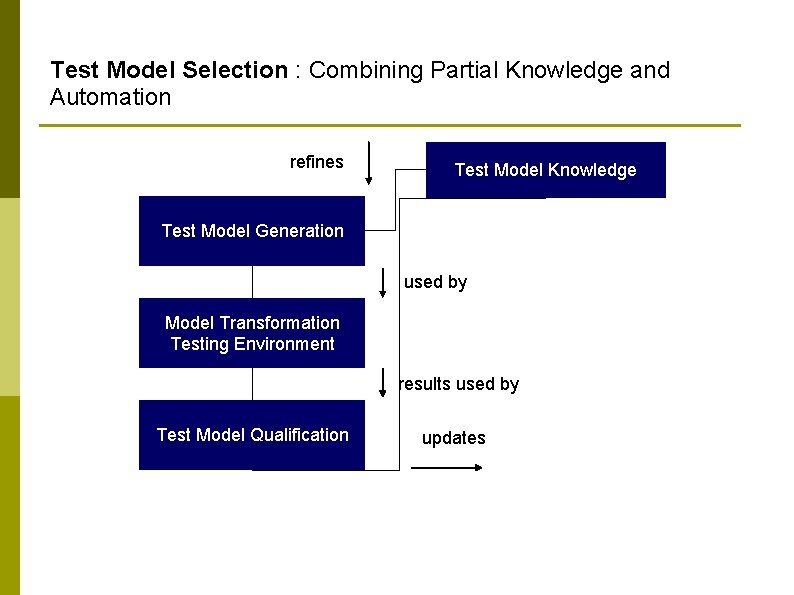
Test Model Selection : Combining Partial Knowledge and Automation refines Test Model Knowledge Test Model Generation used by Model Transformation Testing Environment results used by Test Model Qualification updates

Common Constraint Language : Test Model Generation and Analysis Prolog Alloy 1. A partial instance must be Specified 2. Uses first-order horn clause Logic 3. Cannot specify quantifier based constraints 4. Large set of libraries since Prolog is around for more than two decades. 5. Search is based on Back-tracking in a Warren Abstract Machine 6. Constraint syntax is close to first-order logic 1. Anything from the general depth to partial model can be specified 2. Uses first-order relational logic 3. One can specify quantifier based constraints on a set of atoms 4. Smaller constraint library and interface options with programming languages. 5. Relational model is transformed to boolean logic and solved using an efficient SAT solver. 6. Constraint specification close to object orientation and object constraint language. We tried both for model generation!

Constraint Logic Programming for Model Completion (1) Finite State Machine Meta-model: Ecore Prolog Constraints on Partial Model Instance Modelis. Initial = [HF SMState. Object 1 is. Initial; HFSMState. Object 2 is. Initial; HFSMState. Object 3 is. Initial]; Modelis. Initial : : [0: : 1]; ic global : occurrences(1; Modelis. Initial; 1) CLP Partial Model Instance in Concrete Syntax with 3 State and Transition Objects Expressed as a Graph in the Himesis Graph Library

Constraint Logic Programming for Model Completion (2) Constraint Logic Program in Python (SWI-Prolog) ], : -lib(ic). Transition 0_event: : [1, 2, 3, 4, 5], : -lib(ic_global). Transition 0_exists: : [0. . 1], solve_Model(Model): Transition 1_event: : [1, 2, 3, 4, 5], Model=[ Transition 1_exists: : [0. . 1], Transition 0_event, Transition 2_event: : [1, 2, 3, 4, 5], Transition 0_exists, Transition 2_exists: : [0. . 1], Transition 1_event, State 0_current. State: : [0. . 1], Transition 1_exists, State 0_is. Final: : [0. . 1], Transition 2_event, State 0_is. Initial: : [0. . 1], back-tracking Transition 2_exists, State 0_label: : [0. . 100], State 0_current. State, State 1_current. State: : [0. . 1], State 0_is. Final, State 1_is. Final: : [0. . 1], State 0_is. Initial, State 1_is. Initial: : [0. . 1], State 0_label, State 1_label: : [0. . 100], State 1_current. State, State 2_current. State: : [0. . 1], State 1_is. Final, State 2_is. Final: : [0. . 1], State 1_is. Initial, State 2_is. Initial: : [0. . 1], State 1_label, State 2_label: : [0. . 100], State 2_current. State, . State 2_is. Final, . State 2_is. Initial, Modelis. Initial = [State 1_is. Initial; State 2_label State 2_is. Initial; State 3_is. Initial]; Modelis. Initial : : [0: : 1]; ic global : occurrences(1; Modelis. Initial; 1) labeling(Model). CLP

Disadvantage of using Prolog 1. Constraints are expressed on model instances rather than on meta-model elements. 2. A constraint template needs to be designed that can be applied to any partial model instance by applying constraint of all relevant properties by traversing the partial model. 3. General requirements such as depth or number of type of objects in the desired model instance cannot be easily specified in the language (They have to generated) 4. Only first-order horn clause logic is supported. 5. Its quantifier free. Constraints such as all x: Class | x. is_persistent=true cannot be expressed. 6. The constraint expression is close to theoretical logic and not more natural like OCL. 7. Traditional back-tracking is slower than state-of-the art SAT solvers used for hardware verification. Solution: First-order Relational Logic implemented in Alloy with Kod Relational Model Finder

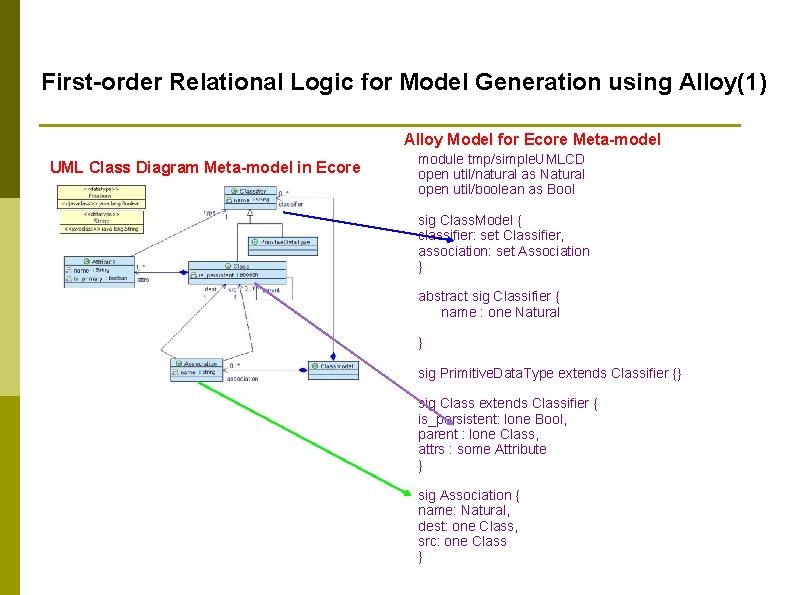
First-order Relational Logic for Model Generation using Alloy(1) Alloy Model for Ecore Meta-model UML Class Diagram Meta-model in Ecore module tmp/simple. UMLCD open util/natural as Natural open util/boolean as Bool sig Class. Model { classifier: set Classifier, association: set Association } abstract sig Classifier { name : one Natural } sig Primitive. Data. Type extends Classifier {} sig Class extends Classifier { is_persistent: lone Bool, parent : lone Class, attrs : some Attribute } Similar tool: UML 2 Alloy sig Association { name: Natural, dest: one Class, src: one Class }

First-order Relational Logic for Model Generation using Alloy(2) Alloy Facts for OCL Constraints fact no. Cyclic. Inheritance { no c: Class | c in c. ^parent } fact unique. Attribute. Names { all c: Class | all a 1: c. attrs , a 2 : c. attrs | a 1. name==a 2. name => a 1 = a 2 } fact all. Different. Attribute. Objects { all c 1: Class, c 2: Class | all a 1: c 1. attrs, a 2: c 2. attrs | a 1==a 2 => c 1=c 2 } fact unique. Classifier. Name { all c 1: Classifier, c 2: Classifier | c 1. name==c 2. name => c 1=c 2 } fact uniqe. Name. Assoc. Src { all a 1: Association, a 2: Association | a 1. name == a 2. name => (a 1 = a 2 or a 1. src != a 2. src) }

First-order Relational Logic for Model Generation using Alloy(3) Alloy Facts for Requirements fact some. Inheritance { some Class. parent } fact atleast. One. Attribute { all c: Class | #c. attrs > 3 } Alloy Run Statement for Generating Objects of different types and depth pred example( ) {} run example for 10 //Depth of 10 run examplea with exactly 1 Class. Model, 2 Class, 3 Association, 20 Attribute Alloy Check Statement for Checking Assertions on Meta-model assert atleast. One. Attribute { all c: Class | #c. attrs > 3 } check atleast. One. Attribute for 10 //Finds a counterexample if the meta-model does not satisfy this requirement for a depth of upto 10

First-order Relational Logic for Model Generation using Alloy(4) : Solving the Model Instance SAT Solver Alloy Model Boolean CNF Formula Model Instance Generated

Conclusion 1. Model Transformation Testing involves the discovery of test input models and black-box testing is the most evident way to go. 2. We present a way to use Partial Model Knowledge, Constrained Input Domain Knowledge expressed as a Meta-model, Tester's requirements, and Model Transformation pre-condition all expressed in different languages to a common constraint language. 3. We experiment with Prolog and with Alloy and conclude that Alloy is the way to go. 4. We intend to use the power of first-order relational logic to develop meta-models and constraints on them to refine the knowledge base both manually and automatically. 5. We intend to build a connection with the imperative programming world where Ecore models can be used in model transformations while we use declarative programming (first-order relational logic) to generate test models from the Ecore.