Computer Vision Projective structure from motion Marc Pollefeys

Computer Vision Projective structure from motion Marc Pollefeys COMP 256 Some slides and illustrations from J. Ponce, …

Computer Vision Last class: Affine camera • The affine projection equations are how to find the origin? or for that matter a 3 D reference point? affine projection preserves center of gravity 2

Computer Vision Orthographic factorization • The orthographic projection equations are • where • All equations can be collected for all i and j • where 3 Note that P and X are resp. 2 mx 3 and 3 xn matrices and therefore the rank of x is at most 3

Computer Vision Orthographic factorization • Factorize m through singular value decomposition • An affine reconstruction is obtained as follows Closest rank-3 approximation yields MLE! 4

Tentative class schedule Computer Vision Jan 16/18 - Introduction Jan 23/25 Cameras Radiometry Sources & Shadows Color Feb 6/8 Linear filters & edges Texture Feb 13/15 Multi-View Geometry Stereo Feb 20/22 Optical flow Project proposals Affine Sf. M Projective Sf. M Camera Calibration Silhouettes and Photoconsistency Mar 13/15 Springbreak Mar 20/22 Segmentation Fitting Mar 27/29 Prob. Segmentation Project Update Tracking Apr 10/12 Object Recognition Apr 17/19 Range data Final project Jan 30/Feb 1 Feb 27/Mar 1 Mar 6/8 Apr 3/5 5 Apr 24/26

Computer Vision PROJECTIVE STRUCTURE FROM MOTION • The Projective Structure from Motion Problem • Elements of Projective Geometry • Projective Structure and Motion from Two Images • Projective Motion from Fundamental Matrices • Projective Structure and Motion from Multiple Images Reading: Chapter 13. 6

Computer Vision The Projective Structure-from-Motion Problem Given m perspective images of n fixed points Pj we can write Problem: estimate the m 3 x 4 matrices M iand the n positions P j from the mn correspondences p. ij 2 mn equations in 11 m+3 n unknowns Overconstrained problem, that can be solved using (non-linear) least squares! 7

Computer Vision The Projective Ambiguity of Projective SFM When the intrinsic and extrinsic parameters are unknown If M i and P are solutions, j So are M’ and P’ where i j and Q is an arbitrary non-singular 4 x 4 matrix. Q is a projective transformation. 8

Computer Vision 9 Projective Spaces: (Semi-Formal) Definition

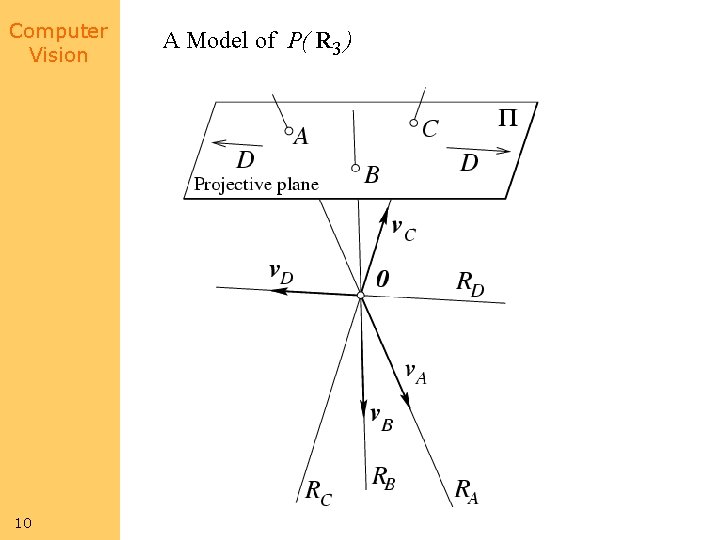
Computer Vision 10 A Model of P( R 3 )

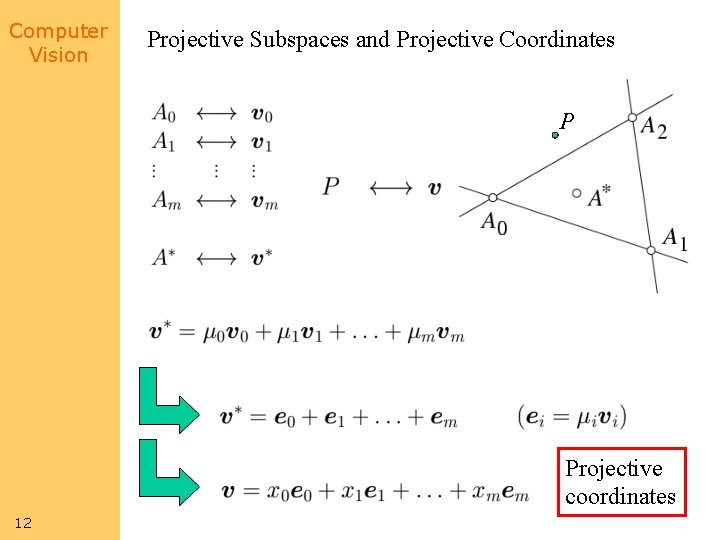
Computer Vision 11 Projective Subspaces and Projective Coordinates

Computer Vision Projective Subspaces and Projective Coordinates P Projective coordinates 12

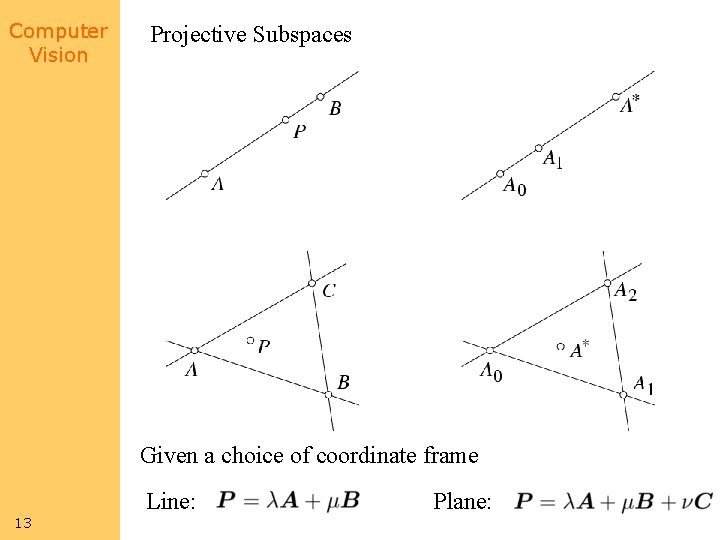
Computer Vision Projective Subspaces Given a choice of coordinate frame 13 Line: Plane:

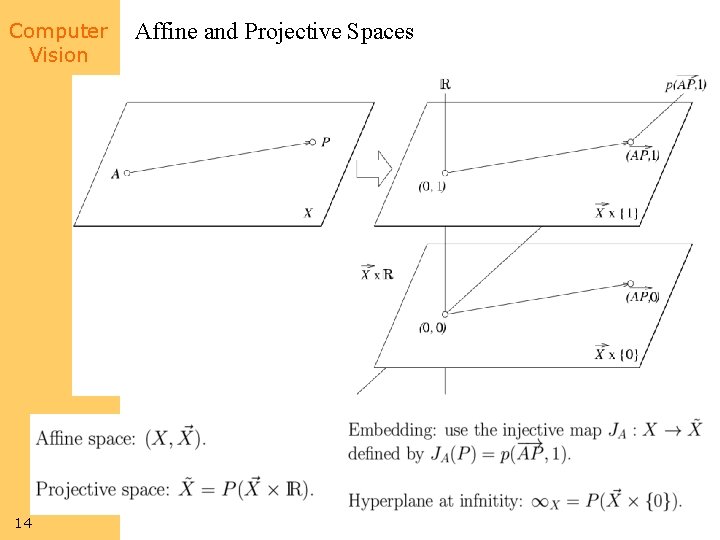
Computer Vision 14 Affine and Projective Spaces

Computer Vision 15 Affine and Projective Coordinates

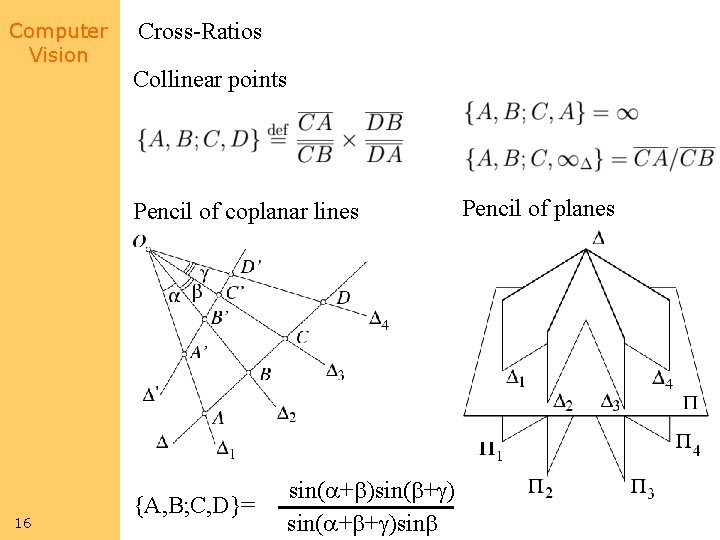
Computer Vision Cross-Ratios Collinear points Pencil of coplanar lines 16 {A, B; C, D}= sin( + ) sin( + + )sin Pencil of planes

Computer Vision Cross-Ratios and Projective Coordinates Along a line equipped with the basis * In a plane equipped with the basis In 3 -space equipped with the basis 17 *

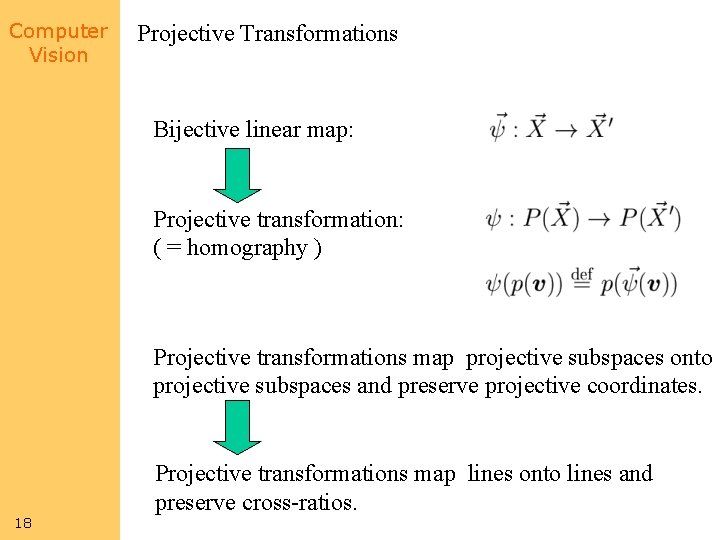
Computer Vision Projective Transformations Bijective linear map: Projective transformation: ( = homography ) Projective transformations map projective subspaces onto projective subspaces and preserve projective coordinates. 18 Projective transformations map lines onto lines and preserve cross-ratios.

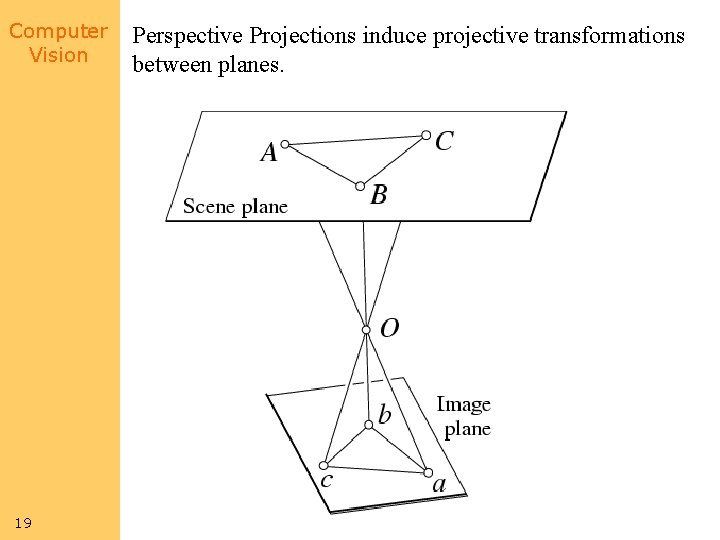
Computer Vision 19 Perspective Projections induce projective transformations between planes.

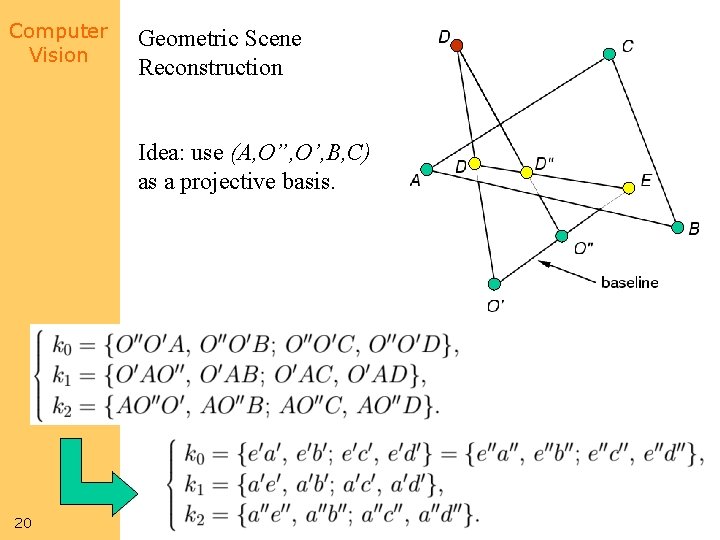
Computer Vision Geometric Scene Reconstruction Idea: use (A, O”, O’, B, C) as a projective basis. 20

Computer Vision 21 Reprinted from “Relative Stereo and Motion Reconstruction, ” by J. Ponce, T. A. Cass and D. H. Marimont, Tech. Report UIUC-BI-AI-RCV-93 -07, Beckman Institute, Univ. of Illinois (1993).

Computer Vision Motion estimation from fundamental matrices Q Once M and M’ are known, P can be computed with LLS. Facts: b’ can be found using LLS. 22

Computer Vision Projective Structure from Motion and Factorization? ? Algorithm (Sturm and Triggs, 1996) • Guess the depths; • Factorize D; • Iterate. 23 Does it converge? (Mahamud and Hebert, 2000)

Computer Vision Bundle adjustment - refining structure and motion • Minimize reprojection error – Maximum Likelyhood Estimation (if error zero-mean Gaussian noise) – Huge problem but can be solved efficiently (exploit sparseness) 24

Computer Vision Bundle adjustment • Developed in photogrammetry in 50´s 25

Computer Vision Non-linear least squares • Linear approximation of residual • allows quadratic approximation of sumof-squares Minimization corresponds to finding zeros of derivative N Levenberg-Marquardt: extra term to deal with singular N (decrease/increase l if success/failure to descent) (extra term = descent term) 26

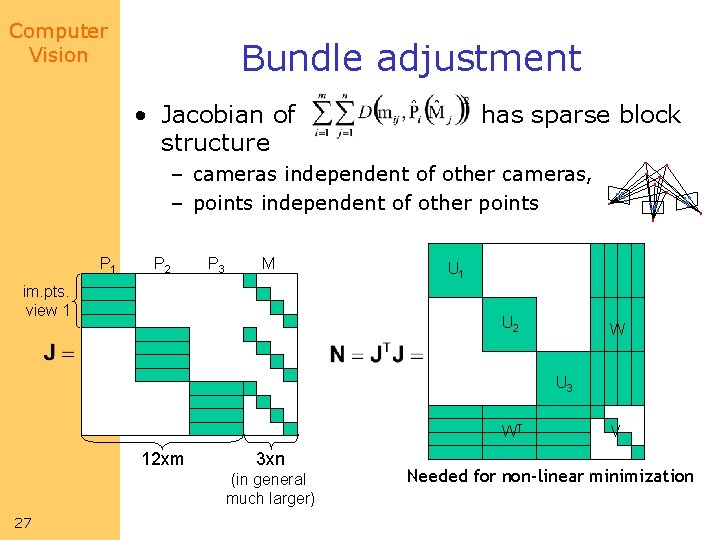
Computer Vision Bundle adjustment • Jacobian of structure has sparse block – cameras independent of other cameras, – points independent of other points P 1 P 2 P 3 M im. pts. view 1 U 2 W U 3 WT 12 xm 3 xn (in general much larger) 27 V Needed for non-linear minimization

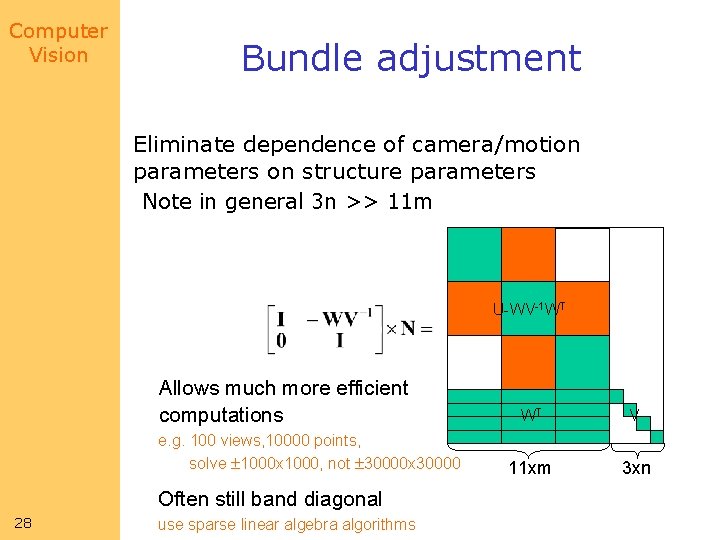
Computer Vision Bundle adjustment Eliminate dependence of camera/motion parameters on structure parameters Note in general 3 n >> 11 m U-WV-1 WT Allows much more efficient computations e. g. 100 views, 10000 points, solve 1000 x 1000, not 30000 x 30000 Often still band diagonal 28 use sparse linear algebra algorithms WT V 11 xm 3 xn

Computer Vision Sequential Sf. M • Initialize motion from two images • Initialize structure • For each additional view – Determine pose of camera – Refine and extend structure • Refine structure and motion 29

Computer Vision Initial projective camera motion • Choose P and P´compatible with F (reference plane; arbitrary) Reconstruction up to projective ambiguity Same for more views? different projective basis 30 • Initialize motion • Initialize structure • For each additional view • Determine pose of camera • Refine and extend structure • Refine structure and motion

Computer Vision Initializing projective structure • Reconstruct matches in projective frame by minimizing the reprojection error Non-iterative optimal solution 31 • Initialize motion • Initialize structure • For each additional view • Determine pose of camera • Refine and extend structure • Refine structure and motion

Computer Vision Projective pose estimation • Infere 2 D-3 D matches from 2 D-2 D matches • Compute pose from (RANSAC, 6 pts) X F x Inliers: 32 • Initialize motion • Initialize structure • For each additional view • Determine pose of camera • Refine and extend structure • Refine structure and motion

Computer Vision Refining and extending structure • Refining structure (Iterative linear) • Extending structure 2 -view triangulation • Initialize motion • Initialize structure • For each additional view 33 • Determine pose of camera • Refine and extend structure • Refine structure and motion

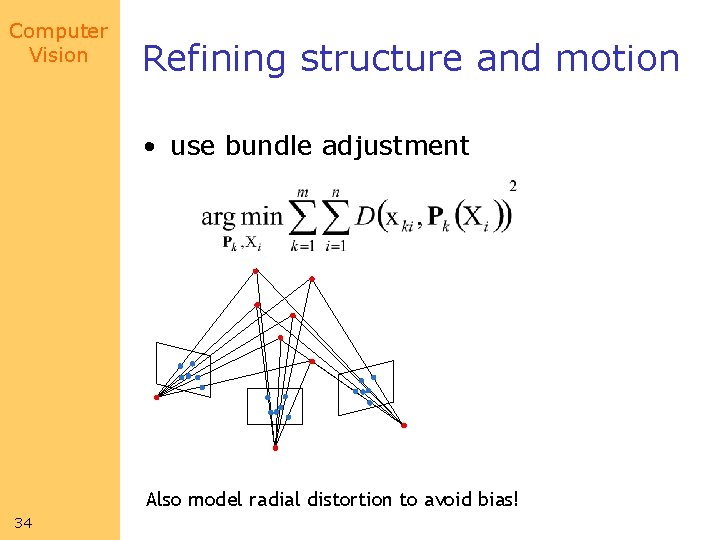
Computer Vision Refining structure and motion • use bundle adjustment Also model radial distortion to avoid bias! 34

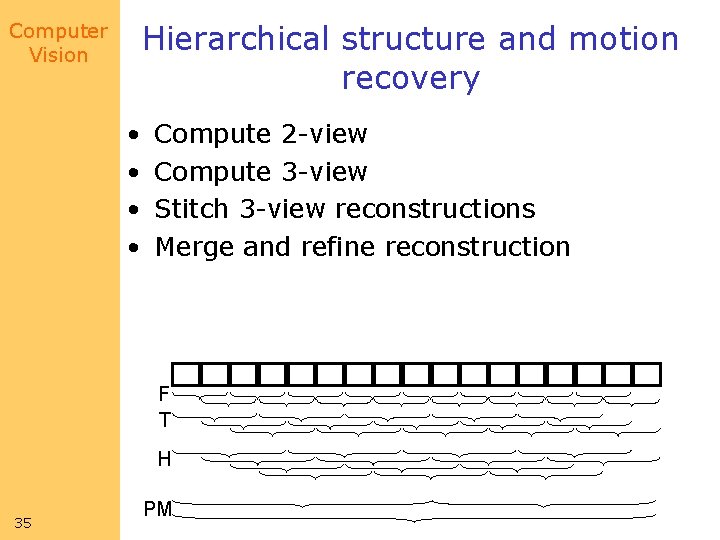
Computer Vision Hierarchical structure and motion recovery • • Compute 2 -view Compute 3 -view Stitch 3 -view reconstructions Merge and refine reconstruction F T H 35 PM

Computer Vision Metric structure and motion use self-calibration (see next class) Note that a fundamental problem of the uncalibrated approach is that it fails if a purely planar scene is observed (in one or more views) (solution possible based on model selection) 36

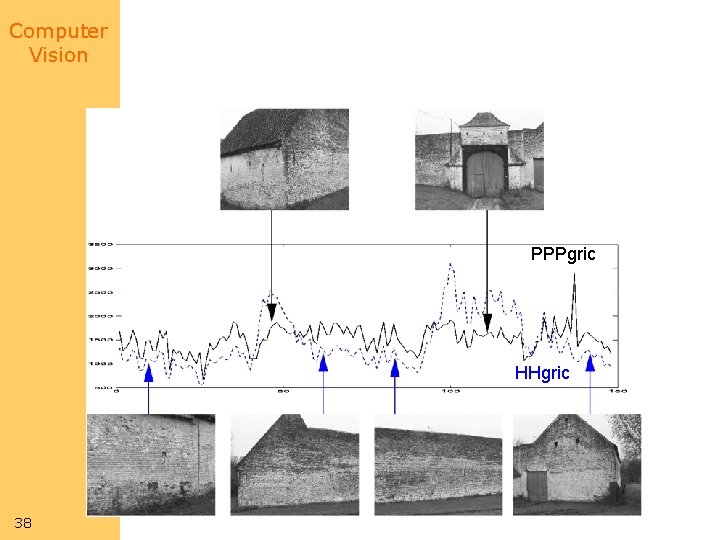
Computer Vision 37 Dealing with dominant planes

Computer Vision PPPgric HHgric 38

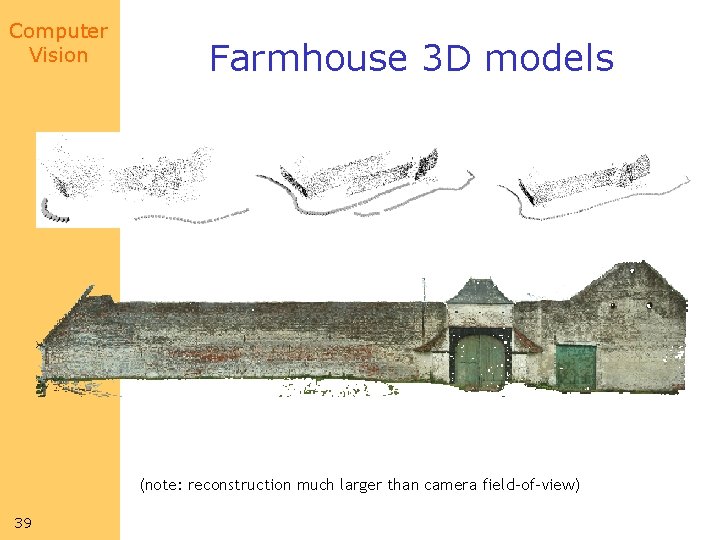
Computer Vision Farmhouse 3 D models (note: reconstruction much larger than camera field-of-view) 39

Computer Vision 40 Application: video augmentation

Computer Vision 41 Next class: Camera calibration (and self-calibration) Reading: Chapter 2 and 3