Computer Vision Optical Flow Some slides from K

Computer Vision Optical Flow Some slides from K. H. Shafique [http: //www. cs. ucf. edu/courses/cap 6411/cap 5415/] and T. Darrell Bahadir K. Gunturk EE 7730 - Image Analysis II

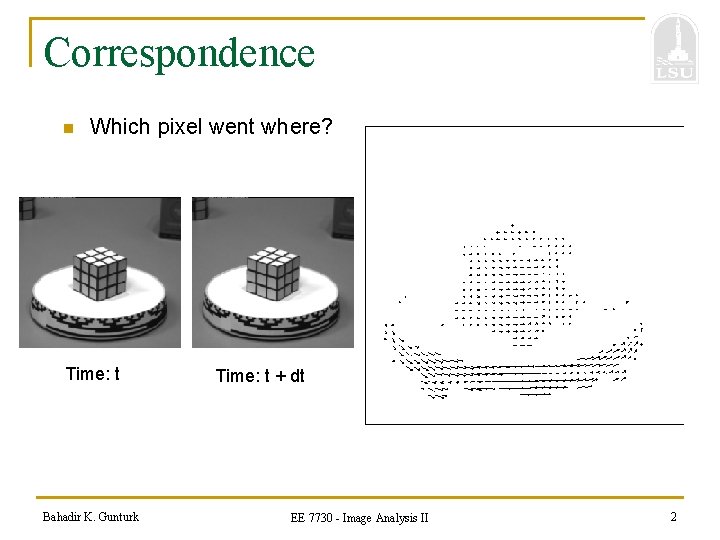
Correspondence n Which pixel went where? Time: t Bahadir K. Gunturk Time: t + dt EE 7730 - Image Analysis II 2

Motion Field vs. Optical Flow n n n Scene flow: 3 D velocities of scene points. Motion field: 2 D projection of scene flow. Optical flow: Approximation of motion field derived from apparent motion of brightness patterns in image. Bahadir K. Gunturk EE 7730 - Image Analysis II 3

Motion Field vs. Optical Flow n Consider perfectly uniform sphere rotating in front of camera. q q n Motion field follows surface points. Optical flow is zero since motion is not visible. Now consider stationary sphere with moving light source. q q Motion field is zero. But optical flow results from changing shading. But, in general, optical flow is a reliable indicator of motion field. Bahadir K. Gunturk EE 7730 - Image Analysis II 4

Applications n n n n Object tracking Video compression Structure from motion Segmentation Correct for camera jitter (stabilization) Combining overlapping images (panoramic image construction) … Bahadir K. Gunturk EE 7730 - Image Analysis II 5

Optical Flow Problem n How to estimate pixel motion from one image to another? Bahadir K. Gunturk EE 7730 - Image Analysis II 6

Computing Optical Flow n Assumption 1: Brightness is constant. n Assumption 2: Motion is small. (from Taylor series expansion) Bahadir K. Gunturk EE 7730 - Image Analysis II 7

Computing Optical Flow n Combine In the limit as u and v goes to zero, the equation becomes exact (optical flow equation) Bahadir K. Gunturk EE 7730 - Image Analysis II 8

Computing Optical Flow n At each pixel, we have one equation, two unknowns. (optical flow equation) n This means that only the flow component in the gradient direction can be determined. The motion is parallel to the edge, and it cannot be determined. This is called the aperture problem. Bahadir K. Gunturk EE 7730 - Image Analysis II 9

Computing Optical Flow n n We need more constraints. The most commonly used assumption is that optical flow changes smoothly locally. Bahadir K. Gunturk EE 7730 - Image Analysis II 10

Computing Optical Flow n One method: The (u, v) is constant within a small neighborhood of a pixel. Optical flow equation: Use a 5 x 5 window: Two unknowns, 25 equation ! Bahadir K. Gunturk EE 7730 - Image Analysis II 11

Computing Optical Flow n Find minimum least squares solution Lucas – Kanade method Bahadir K. Gunturk EE 7730 - Image Analysis II 12

Computing Optical Flow n Lucas – Kanade When is This Solvable? • ATA should be invertible • ATA should not be too small. Other wise noise will be amplified when inverted. ) Bahadir K. Gunturk EE 7730 - Image Analysis II 13

Computing Optical Flow n What are the potential causes of errors in this procedure? q q q Brightness constancy is not satisfied The motion is not small A point does not move like its neighbors n Bahadir K. Gunturk window size is too large EE 7730 - Image Analysis II 14

Improving accuracy n n Recall our small motion assumption This is not exact q n To do better, we need to add higher order terms back in: This is a polynomial root finding problem q Can solve using Newton’s method n q Also known as Newton-Raphson method Lucas-Kanade method does one iteration of Newton’s method n Bahadir K. Gunturk Better results are obtained via more iterations EE 7730 - Image Analysis II 15

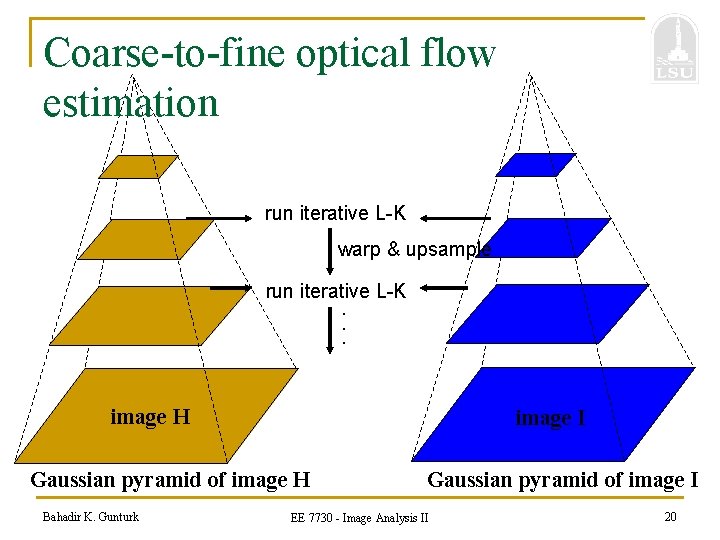
Iterative Refinement n Iterative Lucas-Kanade Algorithm 1. 2. Estimate velocity at each pixel by solving Lucas-Kanade equations Warp H towards I using the estimated flow field - use image warping techniques 3. Repeat until convergence Bahadir K. Gunturk EE 7730 - Image Analysis II 16

Revisiting the small motion assumption n What can we do when the motion is not small? Bahadir K. Gunturk EE 7730 - Image Analysis II 17

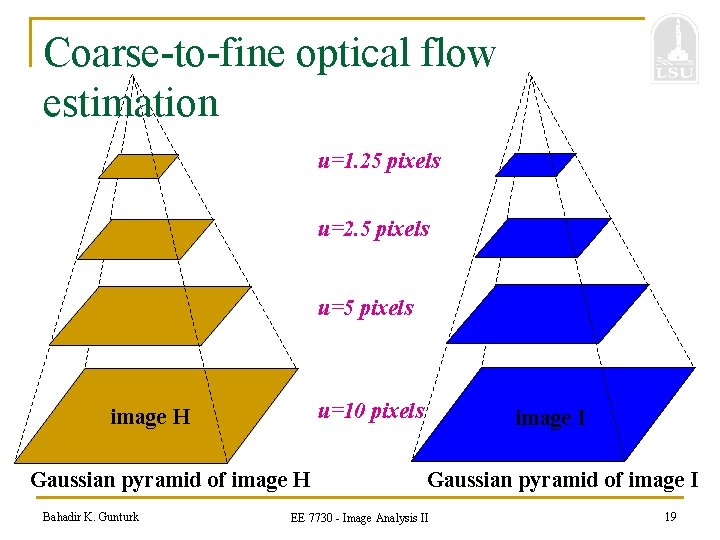
Reduce the resolution! Bahadir K. Gunturk EE 7730 - Image Analysis II 18

Coarse-to-fine optical flow estimation u=1. 25 pixels u=2. 5 pixels u=10 pixels image H Gaussian pyramid of image H Bahadir K. Gunturk image I Gaussian pyramid of image I EE 7730 - Image Analysis II 19

Coarse-to-fine optical flow estimation run iterative L-K warp & upsample run iterative L-K. . . image H image I Gaussian pyramid of image H Bahadir K. Gunturk Gaussian pyramid of image I EE 7730 - Image Analysis II 20

Multi-resolution Lucas-Kanade Algorithm Bahadir K. Gunturk EE 7730 - Image Analysis II 21

Block-Based Motion Estimation Bahadir K. Gunturk EE 7730 - Image Analysis II 22

Block-Based Motion Estimation Bahadir K. Gunturk EE 7730 - Image Analysis II 23

Block-Based Motion Estimation Hierarchical search image H image I Gaussian pyramid of image H Bahadir K. Gunturk Gaussian pyramid of image I EE 7730 - Image Analysis II 24

Parametric (Global) Motion n Sometimes few parameters are enough to represent the motion of whole image translation rotation scale Bahadir K. Gunturk EE 7730 - Image Analysis II 25

Parametric (Global) Motion n Affine Flow Bahadir K. Gunturk EE 7730 - Image Analysis II 26

Parametric (Global) Motion n Affine Flow Bahadir K. Gunturk EE 7730 - Image Analysis II 27

Parametric (Global) Motion n Affine Flow – Approach Bahadir K. Gunturk EE 7730 - Image Analysis II 28

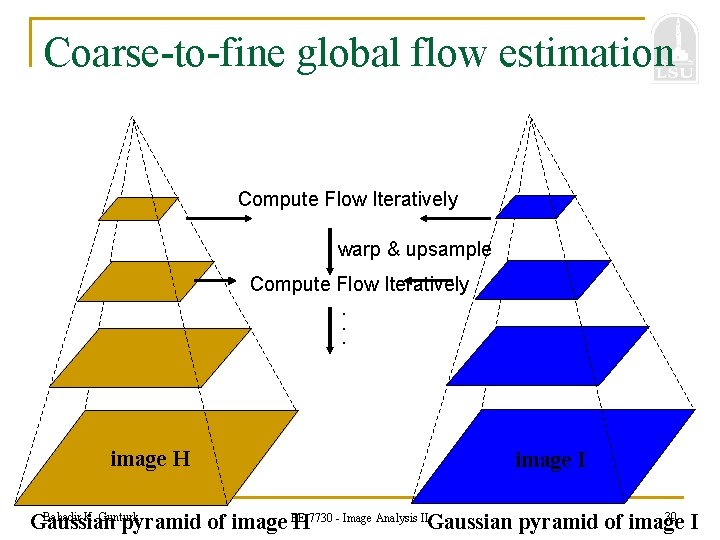
Iterative Refinement n Iterative Estimation 1. 2. Estimate parameters by solving the linear system. Warp H towards I using the estimated flow field - use image warping techniques 3. Repeat until convergence or a fixed number of iterations Bahadir K. Gunturk EE 7730 - Image Analysis II 29

Coarse-to-fine global flow estimation Compute Flow Iteratively warp & upsample Compute Flow Iteratively. . . image H J image I Bahadir K. Gunturk 30 Gaussian pyramid of image EE H 7730 - Image Analysis IIGaussian pyramid of image I

Global Flow Find features Match features Fit parametric model Application: Mosaic construction Bahadir K. Gunturk EE 7730 - Image Analysis II 31

Image Warping Bahadir K. Gunturk EE 7730 - Image Analysis II 32

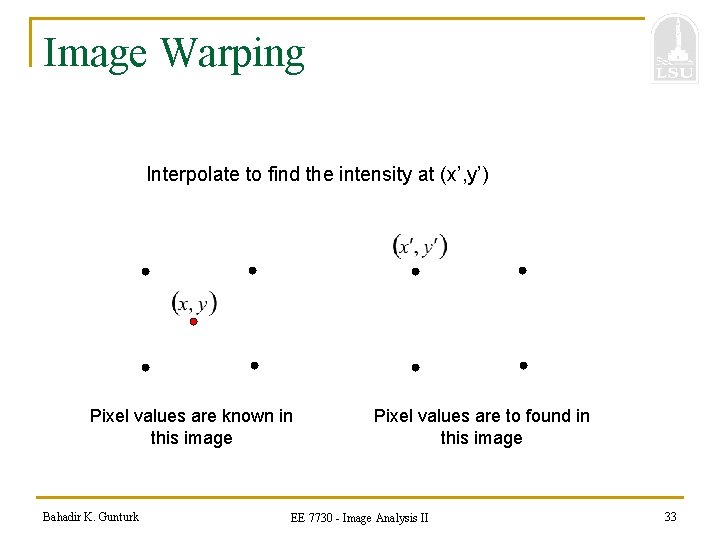
Image Warping Interpolate to find the intensity at (x’, y’) Pixel values are known in this image Bahadir K. Gunturk Pixel values are to found in this image EE 7730 - Image Analysis II 33

Other Parametric Motion Models Perspective and Pseudo-Perspective: Approximation to perspective. (Planar scene + Perspective projection) Bahadir K. Gunturk EE 7730 - Image Analysis II 34