Computer Vision Linear Tracking JanMichael Frahm COMP 256

Computer Vision Linear Tracking Jan-Michael Frahm COMP 256 Some slides from Welch & Bishop

Computer Vision Tracking is the problem of generating an inference about the motion of an object given a sequence of images. The key technical difficulty is maintaining an accurate representation of the posterior on object position given measurements, and doing so efficiently. 2

Computer Vision 3 Examples of tracking

Computer Vision Model for tracking • Object has internal state – Capital indicates random variable – Small represents particular value • Obtained measurements in frame i are – Value of the measurement 4

Computer Vision General Steps of Tracking 1. Prediction: What is the next state of the object given past measurements 2. Data association: Which measures are relevant for the state? 3. Correction: Compute representation of the state from prediction and measurements. 5

Computer Vision Tracking predict 6 correct

Computer Vision Independence Assumptions • Only immediate past matters • Measurements depend only on current state Þ Important simplifications Fortunately it doesn’t limit to much! 7

Computer Vision Linear Dynamic Models • State is linear transformed plus Gaussian noise • Relevant measures are linearly obtained from state plus Gaussian noise • Sufficient to maintain mean and standard deviation 8

Computer Vision A really simple example We are on a boat at night and lost our position We know: • star position 9

Computer Vision Constant Velocity p is position of boat, v is velocity of boat state is We only measure position so 10

Computer Vision Marc makes a measurement Conditional Density Function , -2 11 0 2 4 6 8 10 12 14

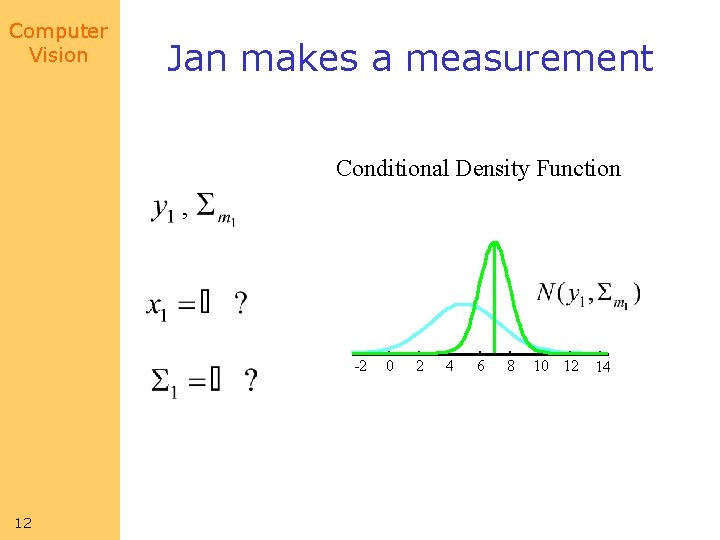
Computer Vision Jan makes a measurement Conditional Density Function , -2 12 0 2 4 6 8 10 12 14

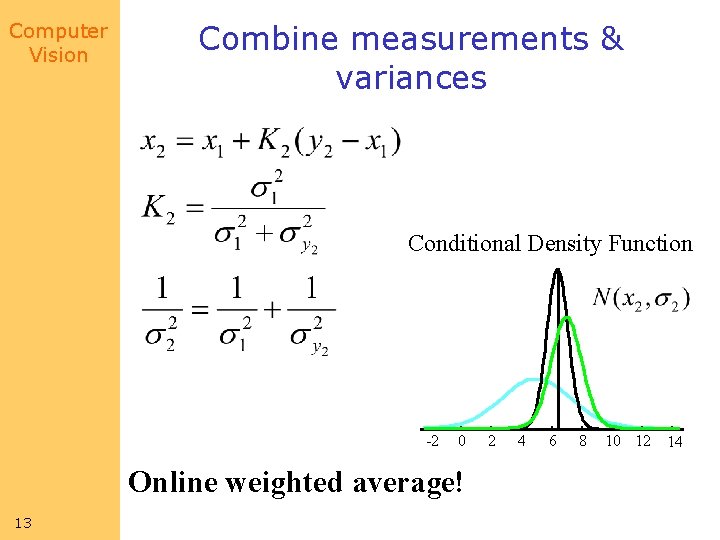
Computer Vision Combine measurements & variances Conditional Density Function -2 0 Online weighted average! 13 2 4 6 8 10 12 14

Computer Vision Rudolf Emil Kalman • • • 14 Born 1930 in Hungary BS and MS from MIT Ph. D 1957 from Columbia Filter developed in 1960 -61 Now retired

Computer Vision Kalman filter • Just some applied math. • A linear dynamic system: f(a+b) = f(a) + f(b) • Noisy data in hopefully less noisy out. • But delay is the price for filtering. . . 15

Computer Vision Predict Correct KF operates by 1. Predicting the new state and its uncertainty 2. Correcting with the new measurement predict 16 correct

Computer Vision What is it used for? • • 17 Tracking missiles Tracking heads/hands/drumsticks Extracting lip motion from video Fitting Bezier patches to point data Lots of computer vision applications Economics Navigation

Computer Vision A really simple example We are on a boat at night and lost our position We know: • move with constant velocity • star position 18

Computer Vision But suppose we’re moving -2 0 2 4 6 • Not all the difference is error. Some may be motion • KF can include a motion model • Estimate velocity and position 19 8 10 12 14

Computer Vision Process Model • Describes how the state changes over time • The state for the first example was scalar • The process model was “nothing changes” • A better model might be constant velocity motion 20

Computer Vision Measurement Model “What you see from where you are” not “Where you are from what you see” 21

Computer Vision Constant Velocity p is position of boat, v is velocity of boat state is We only measure position so 22

Computer Vision State and Error Covariance • First two moments of Gaussian process Process State (Mean) Error Covariance 23

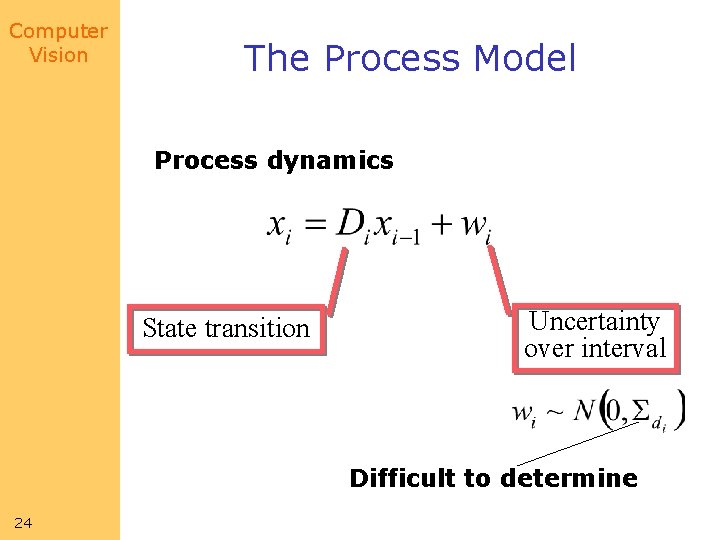
Computer Vision The Process Model Process dynamics State transition Uncertainty over interval Difficult to determine 24

Computer Vision Measurement Model Measurement relationship to state Measurement matrix 25 Measurement uncertainty

Computer Vision Predict (Time Update) a priori state, error covariance, measurement 26

Computer Vision Measurement Update (Correct) a posteriori state and error covariance Kalman gain Minimizes posteriori error covariance 27

Computer Vision The Kalman Gain Weights between prediction and measurements to posteriori error covariance For no measurement uncertainty 28 State is deduced only from measurement

Computer Vision The Kalman Gain Simple univariate (scalar) example a posteriori state and error covariance 29

Computer Vision Summary PREDICT 30 CORRECT

Computer Vision Estimating a Constant The state transition matrix The measurement matrix Prediction 31

Computer Vision 32 Measurement Update

Computer Vision 33 Setup/Initialization

Computer Vision 34 State and Measurements = 0. 1

Computer Vision 35 Error Covariance

Computer Vision 36 State and Measurements =1

Computer Vision 37 State and Measurements = 0. 01

Computer Vision 38 Example camera pose estimation

Computer Vision Kalman Filter Web Site http: //www. cs. unc. edu/~welch/kalman/ • Electronic and printed references – Book lists and recommendations – Research papers – Links to other sites – Some software • News 39

Computer Vision Java-Based KF Learning Tool • On-line 1 D simulation • Linear and non-linear • Variable dynamics http: //www. cs. unc. edu/~welch/kalman / 40

Computer Vision KF Course Web Page http: //www. cs. unc. edu/~tracker/ref/s 2001/kalman/index. html ( http: //www. cs. unc. edu/~tracker/ ) • Java-Based KF Learning Tool • KF web page 41

Computer Vision Closing Remarks • Try it! – Not too hard to understand or program • Start simple – Experiment in 1 D – Make your own filter in Matlab, etc. • Note: the Kalman filter “wants to work” – Debugging can be difficult – Errors can go un-noticed 42

Computer Vision Relevant References • Azarbayejani, Ali, and Alex Pentland (1995). “Recursive Estimation of Motion, Structure, and Focal Length, ” IEEE Trans. Pattern Analysis and Machine Intelligence 17(6): 562 -575. • Dellaert, Frank, Sebastian Thrun, and Charles Thorpe (1998). “Jacobian Images of Super. Resolved Texture Maps for Model-Based Motion Estimation and Tracking, ” IEEE Workshop on Applications of Computer Vision (WACV'98), October, Princeton, NJ, IEEE Computer Society. • http: //mac-welch. cs. unc. edu/~welch/COMP 256/ 43