Computer Vision Linear filters and edges Marc Pollefeys

Computer Vision Linear filters and edges Marc Pollefeys COMP 256

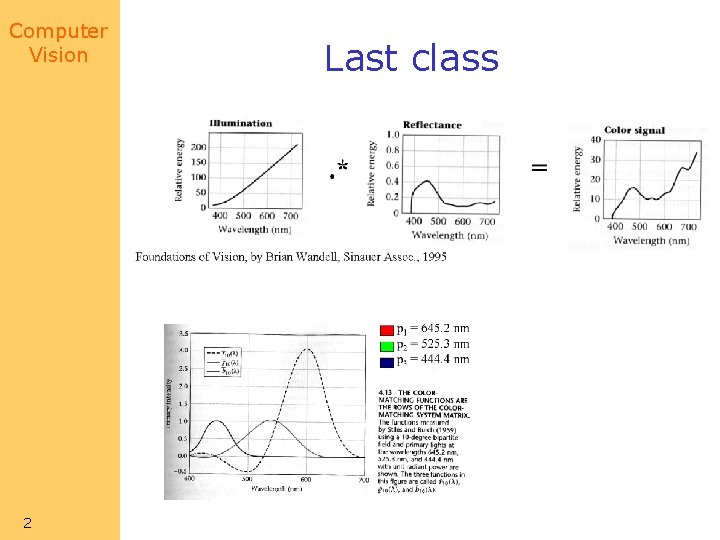
Computer Vision 2 Last class

Computer Vision 3 HSV

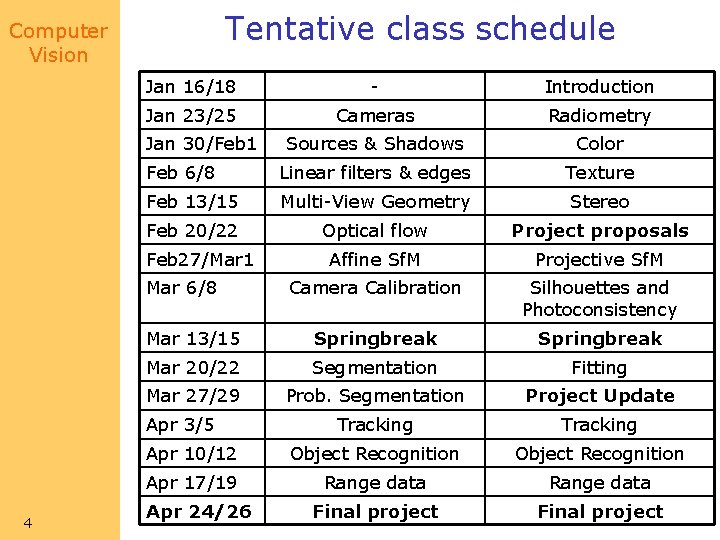
Tentative class schedule Computer Vision Jan 16/18 - Introduction Jan 23/25 Cameras Radiometry Sources & Shadows Color Feb 6/8 Linear filters & edges Texture Feb 13/15 Multi-View Geometry Stereo Feb 20/22 Optical flow Project proposals Affine Sf. M Projective Sf. M Camera Calibration Silhouettes and Photoconsistency Mar 13/15 Springbreak Mar 20/22 Segmentation Fitting Mar 27/29 Prob. Segmentation Project Update Tracking Apr 10/12 Object Recognition Apr 17/19 Range data Final project Jan 30/Feb 1 Feb 27/Mar 1 Mar 6/8 Apr 3/5 4 Apr 24/26

Computer Vision Project • Project proposals – Feb 22 4 minute presentation and 1 -2 page proposal • Project update – Mar 29 4 minute presentation • Final project presentation – Apr 24/26 presentation/demo and short paper-style report • One or more students per project – need identifiable contribution (modules, alternative approaches, …) 5

Computer Vision Project proposals • Some ideas – Vision-based UI (gesture recognition, …) – Tracking people with PTZ camera(s) (single camera, multi camera collaborative) – 3 D reconstruction using Shape-from-? – Camera network calibration – Computer vision on GPU – Environment reconstruction with UAVs –… Come talk to me! 6

Computer Vision Linear Filters • General process: – Form new image whose pixels are a weighted sum of original pixel values, using the same set of weights at each point. • Properties – Output is a linear function of the input – Output is a shiftinvariant function of the input (i. e. shift the input image two pixels to the left, the output is shifted two pixels to the left) 7 • Example: smoothing by averaging – form the average of pixels in a neighbourhood • Example: smoothing with a Gaussian – form a weighted average of pixels in a neighbourhood • Example: finding a derivative – form a weighted average of pixels in a neighbourhood

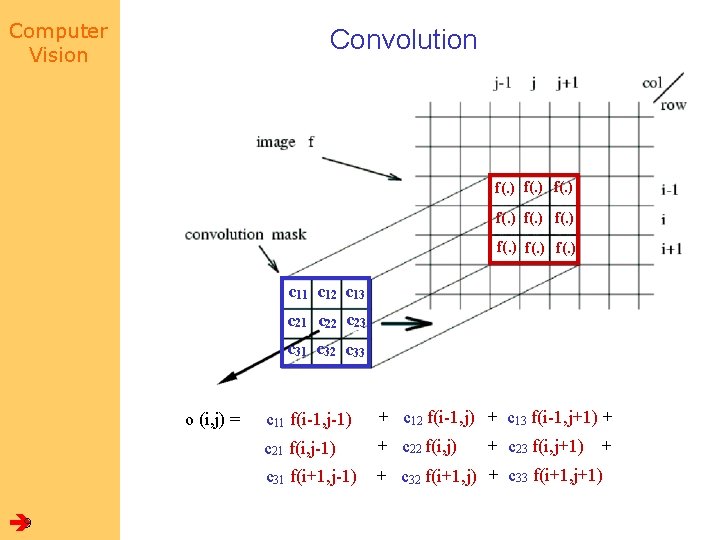
Computer Vision Convolution • Represent these weights as an image, H • H is usually called the kernel • Operation is called convolution – it’s associative 8 • Result is: • Notice wierd order of indices – all examples can be put in this form – it’s a result of the derivation expressing any shift-invariant linear operator as a convolution.

Computer Vision Convolution f(. ) f(. ) c 11 c 12 c 13 c 21 c 22 c 23 c 31 c 32 c 33 o (i, j) = 9 c 11 f(i-1, j-1) + c 12 f(i-1, j) + c 13 f(i-1, j+1) + c 21 f(i, j-1) + c 22 f(i, j) c 31 f(i+1, j-1) + c 32 f(i+1, j) + c 33 f(i+1, j+1) + c 23 f(i, j+1) +

Computer Vision 10 Example: Smoothing by Averaging

Computer Vision Smoothing with a Gaussian • Smoothing with an average actually doesn’t compare at all well with a defocussed lens – Most obvious difference is that a single point of light viewed in a defocussed lens looks like a fuzzy blob; but the • A Gaussian gives a good averaging process model of a fuzzy blob would give a little square. 11

Computer Vision An Isotropic Gaussian • The picture shows a smoothing kernel proportional to (which is a reasonable model of a circularly symmetric fuzzy blob) 12

Computer Vision 13 Smoothing with a Gaussian

Computer Vision Differentiation and convolution • Recall • Now this is linear and shift invariant, so must be the result of a convolution. 14 • We could approximate this as (which is obviously a convolution; it’s not a very good way to do things, as we shall see)

Computer Vision 15 Finite differences

Computer Vision Noise • Simplest noise model – independent stationary additive Gaussian noise – the noise value at each pixel is given by an independent draw from the same normal probability distribution 16 • Issues – this model allows noise values that could be greater than maximum camera output or less than zero – for small standard deviations, this isn’t too much of a problem - it’s a fairly good model – independence may not be justified (e. g. damage to lens) – may not be stationary (e. g. thermal gradients in the ccd)

Computer Vision sigma=1 17

Computer Vision sigma=16 18

Computer Vision Finite differences and noise • Finite difference filters respond strongly to noise – obvious reason: image noise results in pixels that look very different from their neighbours • Generally, the larger the noise the stronger the response 19 • What is to be done? – intuitively, most pixels in images look quite a lot like their neighbours – this is true even at an edge; along the edge they’re similar, across the edge they’re not – suggests that smoothing the image should help, by forcing pixels different to their neighbours (=noise pixels? ) to look more like neighbours

Computer Vision Finite differences responding to noise Increasing noise -> (this is zero mean additive gaussian noise) 20

Computer Vision The response of a linear filter to noise • Do only stationary independent additive Gaussian noise with zero mean (non-zero mean is easily dealt with) • Mean: – output is a weighted sum of inputs – so we want mean of a weighted sum of zero mean normal random variables – must be zero 21 • Variance: – recall • variance of a sum of random variables is sum of their variances • variance of constant times random variable is constant^2 times variance – then if s is noise variance and kernel is K, variance of response is

Computer Vision Filter responses are correlated • over scales similar to the scale of the filter • Filtered noise is sometimes useful – looks like some natural textures, can be used to simulate fire, etc. 22

Computer Vision 23

Computer Vision 24

Computer Vision 25

Computer Vision Smoothing reduces noise • Generally expect pixels to “be like” their neighbours – surfaces turn slowly – relatively few reflectance changes • Generally expect noise processes to be independent from pixel to pixel 26 • Implies that smoothing suppresses noise, for appropriate noise models • Scale – the parameter in the symmetric Gaussian – as this parameter goes up, more pixels are involved in the average – and the image gets more blurred – and noise is more effectively suppressed

Computer Vision The effects of smoothing Each row shows smoothing with gaussians of different width; each column shows different realisations of an image of gaussian noise. 27

Computer Vision Some other useful filtering techniques • Median filter • Anisotropic diffusion 28

Computer Vision Median filters : principle non-linear filter method : n 1. rank-order neighbourhood intensities n 2. take middle value no new grey levels emerge. . . 29

Computer Vision Median filters : odd-man-out advantage of this type of filter is its “odd-man-out” effect e. g. 1, 1, 1, 7, 1, 1 ? , 1, 1, 1, ? 30

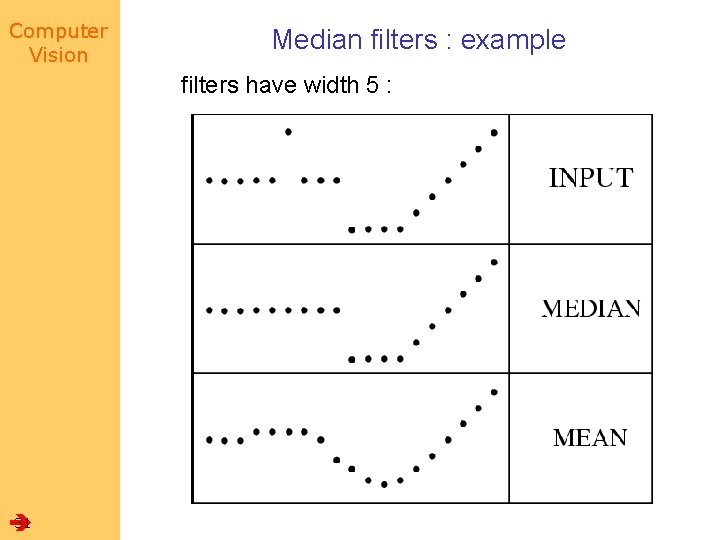
Computer Vision Median filters : example filters have width 5 : 31

Computer Vision Median filters : analysis median completely discards the spike, linear filter always responds to all aspects median filter preserves discontinuities, linear filter produces rounding-off effects DON’T become all too optimistic 32

Computer Vision Median filter : images 3 x 3 median filter : sharpens edges, destroys edge cusps and protrusions 33

Computer Vision Median filters : Gauss revisited Comparison with Gaussian : e. g. upper lip smoother, eye better preserved 34

Computer Vision Example of median 10 times 3 X 3 median 35 patchy effect important details lost (e. g. ear-ring)

Computer Vision Gradients and edges • Points of sharp change in an image are interesting: – change in reflectance – change in object – change in illumination – noise • Sometimes called edge points 36 • General strategy – determine image gradient – now mark points where gradient magnitude is particularly large wrt neighbours (ideally, curves of such points).

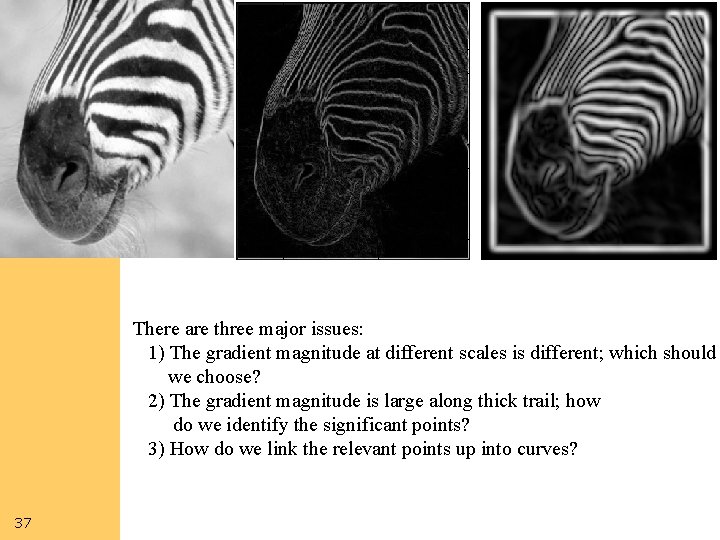
Computer Vision There are three major issues: 1) The gradient magnitude at different scales is different; which should we choose? 2) The gradient magnitude is large along thick trail; how do we identify the significant points? 3) How do we link the relevant points up into curves? 37

Computer Vision Smoothing and Differentiation • Issue: noise – smooth before differentiation – two convolutions to smooth, then differentiate? – actually, no - we can use a derivative of Gaussian filter • because differentiation is convolution, and convolution is associative 38

Computer Vision 1 pixel 3 pixels 7 pixels The scale of the smoothing filter affects derivative estimates, and also the semantics of the edges recovered. 39

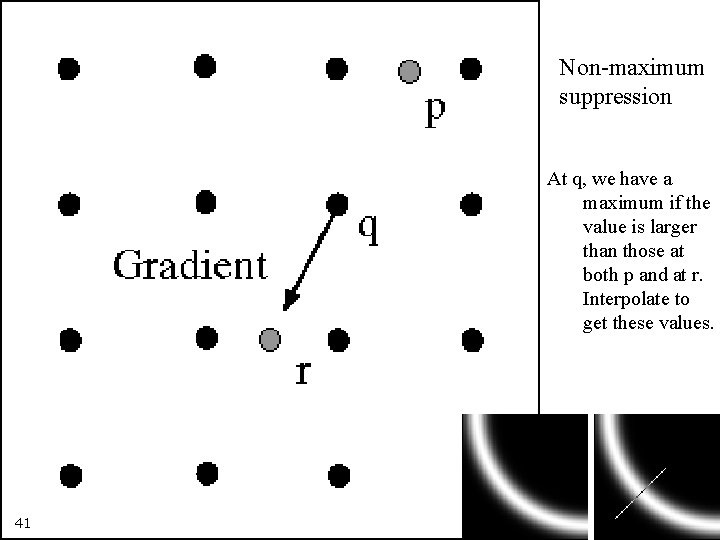
Computer Vision We wish to mark points along the curve where the magnitude is biggest. We can do this by looking for a maximum along a slice normal to the curve (non-maximum suppression). These points should form a curve. There are then two algorithmic issues: at which point is the maximum, and where is the next one? 40

Computer Vision Non-maximum suppression At q, we have a maximum if the value is larger than those at both p and at r. Interpolate to get these values. 41

Computer Vision Predicting the next edge point Assume the marked point is an edge point. Then we construct the tangent to the edge curve (which is normal to the gradient at that point) and use this to predict the next points (here either r or s). 42

Computer Vision Remaining issues • Check that maximum value of gradient value is sufficiently large – drop-outs? use hysteresis • use a high threshold to start edge curves and a low threshold to continue them. 43

Computer Vision Notice • Something nasty is happening at corners • Scale affects contrast • Edges aren’t bounding contours 44

Computer Vision 45

Computer Vision fine scale high threshold 46

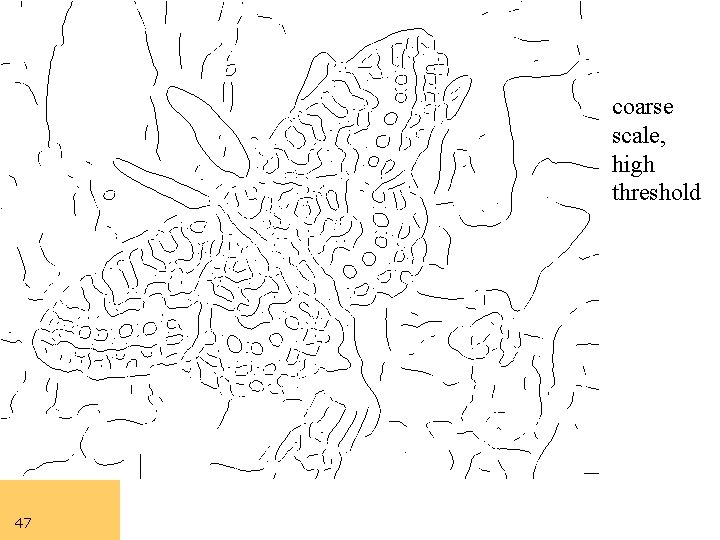
Computer Vision coarse scale, high threshold 47

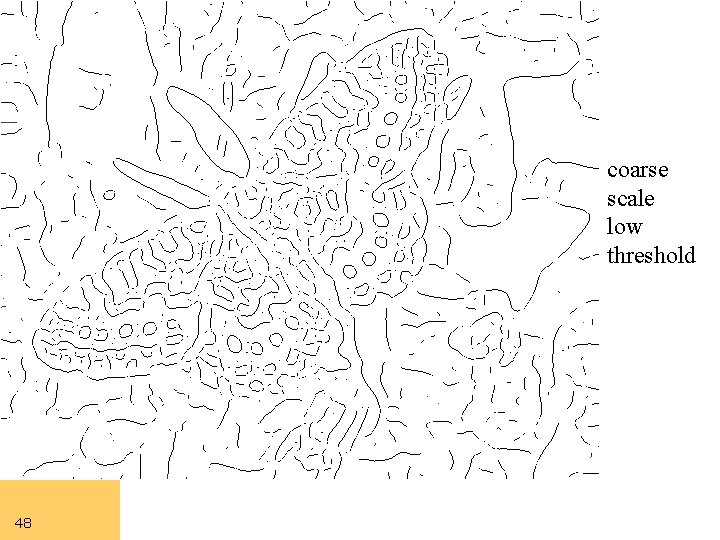
Computer Vision coarse scale low threshold 48

Computer Vision Filters are templates • Applying a filter at some point can be seen as taking a dotproduct between the image and some vector • Filtering the image is a set of dot products 49 • Insight – filters look like the effects they are intended to find – filters find effects they look like

Computer Vision Normalized correlation • Think of filters of a dot product – now measure the angle – i. e normalised correlation output is filter output, divided by root sum of squares of values over which filter lies 50 • Tricks: – ensure that filter has a zero response to a constant region (helps reduce response to irrelevant background) – subtract image average when computing the normalizing constant (i. e. subtract the image mean in the neighbourhood) – absolute value deals with contrast reversal

Computer Vision Positive responses Zero mean image, -1: 1 scale 51 Zero mean image, -max: max scale

Computer Vision Positive responses Zero mean image, -1: 1 scale 52 Zero mean image, -max: max scale

Computer Vision Figure from “Computer Vision for Interactive Computer Graphics, ” W. Freeman et al, IEEE Computer Graphics and Applications, 1998 copyright 1998, IEEE 53

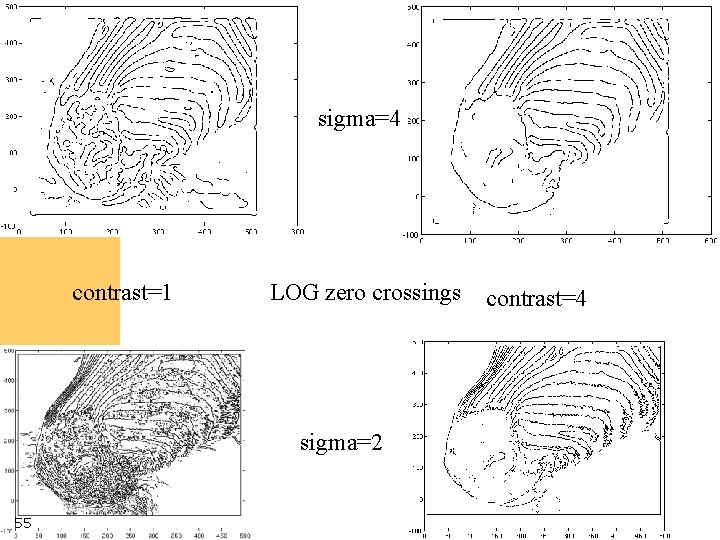
Computer Vision The Laplacian of Gaussian • Another way to detect an extremal first derivative is to look for a zero second derivative • Appropriate 2 D analogy is rotation invariant – the Laplacian • Bad idea to apply a Laplacian without smoothing – smooth with Gaussian, apply Laplacian – this is the same as filtering with a Laplacian of Gaussian filter • Now mark the zero points where there is a sufficiently large derivative, and enough contrast 54

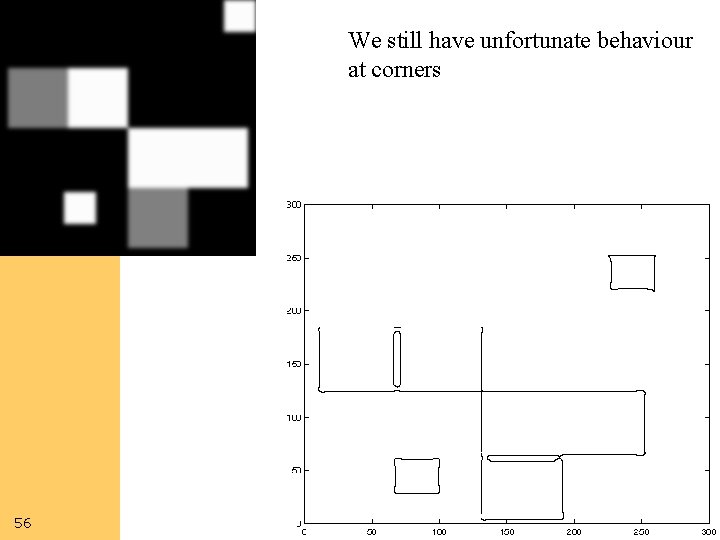
Computer Vision sigma=4 contrast=1 LOG zero crossings sigma=2 55 contrast=4

Computer Vision 56 We still have unfortunate behaviour at corners

Computer Vision Orientation representations • The gradient magnitude is affected by illumination changes – but it’s direction isn’t • We can describe image patches by the swing of the gradient orientation • Important types: – constant window • small gradient mags – edge window • few large gradient mags in one direction – flow window • many large gradient mags in one direction – corner window • large gradient mags that swing 57

Computer Vision Representing Windows • Types – constant • small eigenvalues – Edge • one medium, one small – Flow • one large, one small – corner • two large eigenvalues 58

Computer Vision 59

Computer Vision 60

Computer Vision 61

Computer Vision 62

Computer Vision 63 Next class: Pyramids and Texture F&P Chapter 9