Computer Vision I The Fourier Transform part 1









![Fourier series (1) Fourier series [wikipedia] 25/10/2021 Computer Vision I: Fourier Transform 11 Fourier series (1) Fourier series [wikipedia] 25/10/2021 Computer Vision I: Fourier Transform 11](https://slidetodoc.com/presentation_image_h2/e91316ad23a5c0852f94a80a7fe86cbe/image-11.jpg)


![Fourier transform: properties if … f(x) is real then … F(-k) = [F(k)]* f(x) Fourier transform: properties if … f(x) is real then … F(-k) = [F(k)]* f(x)](https://slidetodoc.com/presentation_image_h2/e91316ad23a5c0852f94a80a7fe86cbe/image-14.jpg)















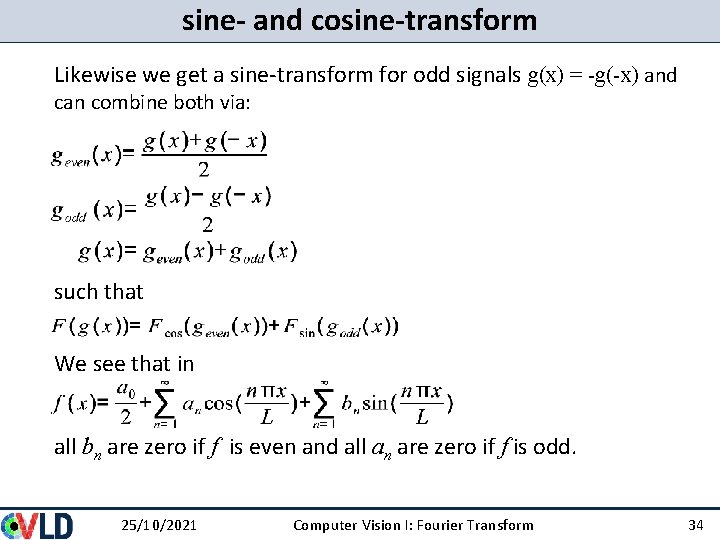













- Slides: 49

Computer Vision I The Fourier Transform part 1: basics Holger Heidrich 25/10/2021 Computer Vision I: Fourier Transform

Roadmap this lecture part 1: theoretical background • Superposition principle • Definition, properties • Convolution • sampling theorem, connection discrete continuous, image pyramids • Fast Fourier Transform • Correlation, Autocorrelation • Regularisation • uncertainty principle part 2 : applications • Fourier descriptors • Fourier slice photography • Optics: Lens as F-transformer, 4 -f • (microscopy, holography, Optic design) • (Video Magnification) 25/10/2021 Computer Vision I: Fourier Transform 2

Literature 1. Stanford course: The Fourier Transforms and Its Applications and their course reader 2. J. F. James, A Student’s Guide to Fourier Transforms 3. Chen, Haykin, On Different Facets of Regularization Theory 4. Max Born, Emil Wolf, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light 5. Joseph W. Goodman, Introduction to Fourier Optics 6. Ren Ng, Fourier slice photography 25/10/2021 Computer Vision I: Fourier Transform 3

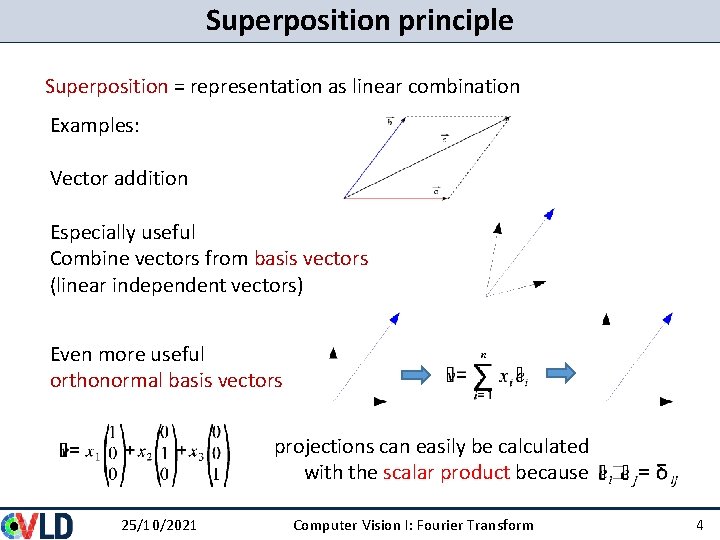
Superposition principle Superposition = representation as linear combination Examples: Vector addition Especially useful Combine vectors from basis vectors (linear independent vectors) Even more useful orthonormal basis vectors projections can easily be calculated with the scalar product because 25/10/2021 Computer Vision I: Fourier Transform 4

Superposition principle Superposition = representation as linear combination: same idea for functions: split a function into pointwise contributions with the -function (distribution) built a rect- from step-functions [wiki] 25/10/2021 Computer Vision I: Fourier Transform 5

Superposition principle the superposition principle is applicable to linear systems example: heat equation because differentiation is a linear operator we can decompose our heat distribution into weighted sums of easier functions (e. g. single points) and combine the solutions Fourier (Théorie analytique de la chaleur. Paris 1822) has chosen to decompose u into sine and cosine functions. Jean Baptiste Joseph Fourier 1768 -1830 Why? 25/10/2021 Computer Vision I: Fourier Transform 6

Fourier transform: intro two reasons to use Fourier transform (1) mathematical: • differentiation does not change the function type: • consider the series with we can verify Eulers Formula 25/10/2021 Computer Vision I: Fourier Transform 7

reminder: complex numbers 25/10/2021 Computer Vision I: Fourier Transform 8

Fourier transform: intro two reasons to use Fourier transform (2) practical: • periodic functions (in time and/or space): rotations, oscillations, vibrations, waves, . . . • functions can be made periodic by repetition 25/10/2021 Computer Vision I: Fourier Transform 9

Fourier series have period and therefore we can decompose periodic functions as Fourier series: How to get the coefficients? Project onto the basis! 25/10/2021 Computer Vision I: Fourier Transform 10
![Fourier series 1 Fourier series wikipedia 25102021 Computer Vision I Fourier Transform 11 Fourier series (1) Fourier series [wikipedia] 25/10/2021 Computer Vision I: Fourier Transform 11](https://slidetodoc.com/presentation_image_h2/e91316ad23a5c0852f94a80a7fe86cbe/image-11.jpg)
Fourier series (1) Fourier series [wikipedia] 25/10/2021 Computer Vision I: Fourier Transform 11

Fourier series - complex representation and Eulers Formula with frequency 25/10/2021 angular frequency Computer Vision I: Fourier Transform 12

Fourier transform: definition if f(x) is • absolute integrable and • oscillates in every finite interval only finitely many times, than, with x, k – vectors, n – dimension Fourier transform: Inverse Fourier transform: 25/10/2021 Computer Vision I: Fourier Transform 13
![Fourier transform properties if fx is real then Fk Fk fx Fourier transform: properties if … f(x) is real then … F(-k) = [F(k)]* f(x)](https://slidetodoc.com/presentation_image_h2/e91316ad23a5c0852f94a80a7fe86cbe/image-14.jpg)
Fourier transform: properties if … f(x) is real then … F(-k) = [F(k)]* f(x) is imaginary F(-k) = -[F(k)]* f(x) is even F(-k) = F(k) (even) f(x) is odd F(-k) = -F(k) (odd) f(x) is real and even F(k) is real and even f(x) is real and odd F(k) is imaginary and odd f(x) is imaginary and even F(k) is imaginary and even f(x) is imaginary and odd F(k) is real and odd 25/10/2021 Computer Vision I: Fourier Transform 14

Fourier transform: properties (scaling) (shift) Parsevalsches Theorem: 25/10/2021 Computer Vision I: Fourier Transform 15

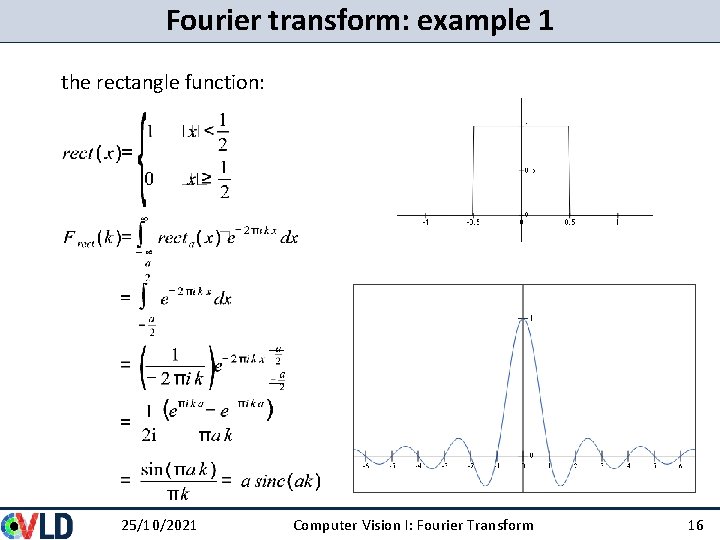
Fourier transform: example 1 the rectangle function: 25/10/2021 Computer Vision I: Fourier Transform 16

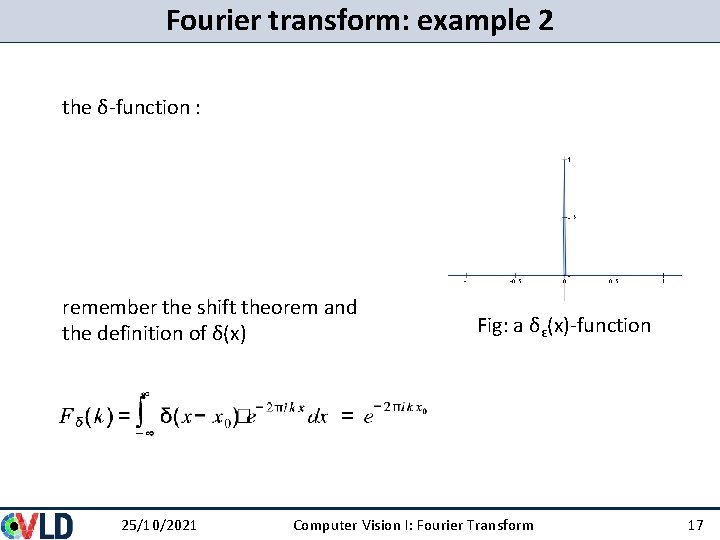
Fourier transform: example 2 the δ-function : remember the shift theorem and the definition of δ(x) 25/10/2021 Fig: a δε(x)-function Computer Vision I: Fourier Transform 17

Fourier transform: periodic example remember: • functions with finite support can be made periodic by repetition, lets try this with δ(x): This repeats with period b. What is the Fourier transform? Periodic with 1/nb and so with 1/b. Thus summands are 1 at k=m/b and have arbitrary many sign changes in-between. 25/10/2021 Computer Vision I: Fourier Transform 18

Fourier transform: periodic example 25/10/2021 Computer Vision I: Fourier Transform 19

Fourier transform: convolution What does this convolution mean at all? The function g is moved to x (via (y-x)) and mirrored (-(y-x)=(x-y)), then the resulting function is multiplied with f and integrated giving the value of the convolution h at x. [image and more illustration: Wiki] If one of the functions is symmetric (even), like the δfunction, a rect or a Gaussian, the mirroring does not have any effect. 25/10/2021 Computer Vision I: Fourier Transform 20

Fourier transform: convolution How can we make other functions periodic? Use the replication property of the δ-function at every position of the comb: 25/10/2021 Computer Vision I: Fourier Transform 21

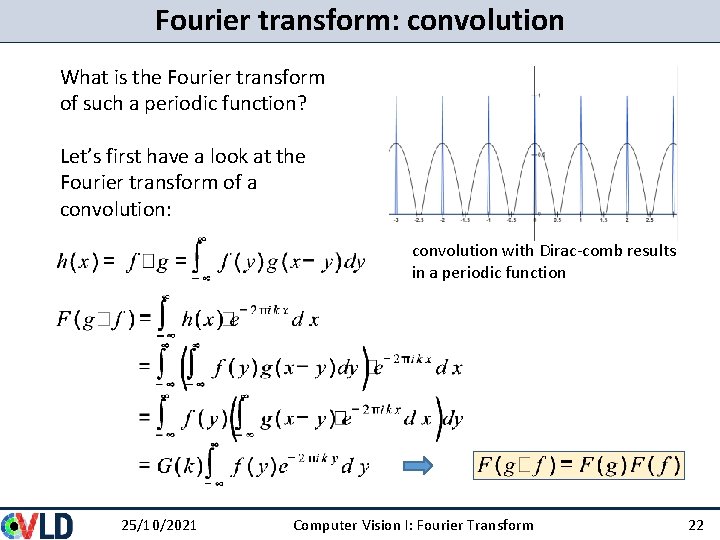
Fourier transform: convolution What is the Fourier transform of such a periodic function? Let’s first have a look at the Fourier transform of a convolution: convolution with Dirac-comb results in a periodic function 25/10/2021 Computer Vision I: Fourier Transform 22

Fourier transform: convolution What is the Fourier transform of such a periodic function? A periodic function has a discrete Fourier transform - therefore we can develop it into a Fourier series. 25/10/2021 Computer Vision I: Fourier Transform 23

Fourier transform: sampling Let’s assume that the Fourier transform of a function g(x) is zero outside an interval ±k. N. Then: and even A band-limited function in the Fourier domain. . applying Fourier transform of product and convolution 25/10/2021 Computer Vision I: Fourier Transform 24

Fourier transform: sampling Sampling theorem If the Fourier transform of a function g(x) is zero outside an interval ±k. N, i. e. it is bandlimited, then g(x) can be interpolated from its sample points of distance at most A band-limited function in the Fourier domain. . 2 k. N - Nyquist frequency 25/10/2021 Computer Vision I: Fourier Transform 25

Fourier transform: aliasing Aliasing What if we sample not dense enough? The repetitions of the Fourier transform of g(x) will overlap: high frequency components will be added to low frequency components. g(x) cannot be recovered from the samples anymore. [Img: Wiki] 25/10/2021 Overlapping spectra due to sampling below the Nyquist rate. Computer Vision I: Fourier Transform 26

aliasing : image pyramids Image pyramids (Lect. 3) are an application of the sampling theorem: If we want to scale down an image, i. e. use only every other pixel, we have to reduce the resolution first by reducing the width of its spectrum by a factor of two. Overlapping spectra due to sampling below the Nyquist rate. 25/10/2021 Computer Vision I: Fourier Transform 27

discrete Fourier transform Combine what we know about periodic functions: Let g(x) be a discrete and periodic function. In the image domain, we can think of an infinitely repeating (digital) image. 25/10/2021 Computer Vision I: Fourier Transform 28

discrete Fourier transform Let g(x) be a discrete and periodic function. Then the Fourier transform G(k) has to be discrete because g(x) is periodic, and periodic because g(x) is discrete. This leads to the discrete Fourier transform pair: 25/10/2021 Computer Vision I: Fourier Transform 29

discrete Fourier transform A note on periodicity: In k = N-1 gives the same as k=-1 and is therefore a lower frequency than k=N-2. The same for k up to N/2. So symmetry is rather from k=-N/2+1 to k= N/2, besides the fact, that Fourier transform code often choses to go from 0 to N-1. E. g. in Open. CV you get (left) and have to rearrange to see the zero component in the middle of the image (right). 25/10/2021 Computer Vision I: Fourier Transform 30

discrete Fourier transform So our signal (image) and its discrete Fourier transform are parts of endless repeating patterns. Still we have some choice in the layout of this pattern. Moving the centre to the origin results in a phase Factor of: i. e. a minus-sign for odd frequencies. 25/10/2021 Computer Vision I: Fourier Transform 31

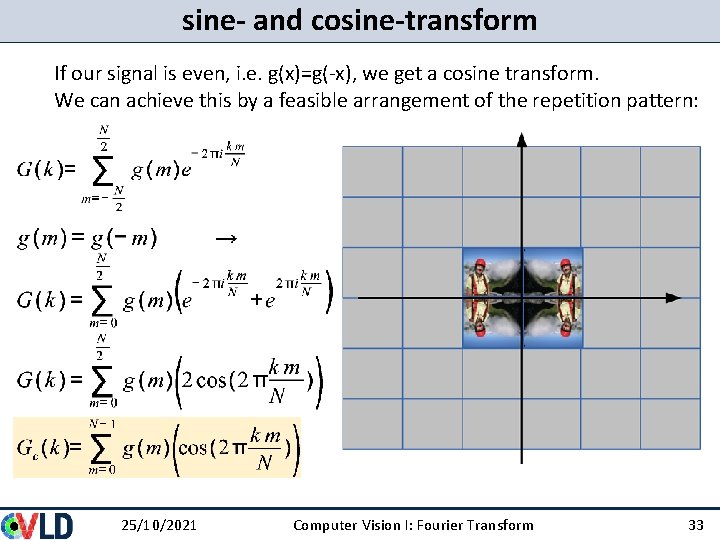
sine- and cosine-transform If our signal is even, i. e. g(x)=g(-x), all imaginary parts cancel out: 25/10/2021 Computer Vision I: Fourier Transform 32

sine- and cosine-transform If our signal is even, i. e. g(x)=g(-x), we get a cosine transform. We can achieve this by a feasible arrangement of the repetition pattern: 25/10/2021 Computer Vision I: Fourier Transform 33
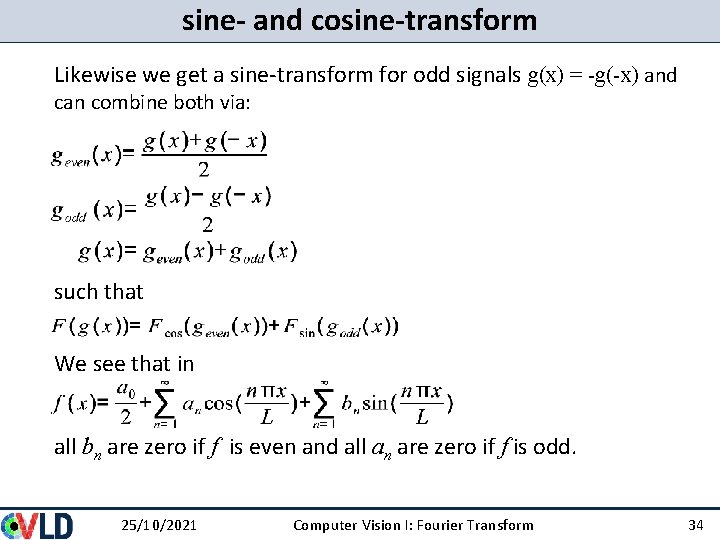
sine- and cosine-transform Likewise we get a sine-transform for odd signals g(x) = -g(-x) and can combine both via: such that We see that in all bn are zero if f is even and all an are zero if f is odd. 25/10/2021 Computer Vision I: Fourier Transform 34

Fast Fourier Transform The Fast Fourier Transform (FFT) is a method to reduce the complexity of the DFT from O(N²) to O( N log N ). Consider N=2 : 25/10/2021 Computer Vision I: Fourier Transform 35

Fast Fourier Transform The Fast Fourier Transform (FFT) is a method to reduce the complexity of the DFT from O(N²) to O( N log N ). Consider N=2 : And N=4 : Combine the FFT of even and odd values to reuse calculations, do this recursively! 25/10/2021 Computer Vision I: Fourier Transform 36

DFT in 2 D We already defined the Fourier transform in multiple dimensions. For completeness here is what the DFT looks like in 2 D: R - Rows C - Columns 25/10/2021 An Image is a weighted sum of images like this. Computer Vision I: Fourier Transform 37

Fourier transform: convolution What does this convolution mean at all? The function g is moved to x (via (y-x)) and mirrored (-(y-x)=(x-y)), then the resulting function is multiplied with f and integrated giving the value of the convolution h at x. [image and more illustration: Wiki] If one of the functions is symmetric (even), like the δfunction, a rect or a Gaussian, the mirroring does not have any effect. 25/10/2021 Computer Vision I: Fourier Transform 38

Fourier transform: convolution Because of convolution is also called filtering. This formula gives the impact of filters (Lect. 3) on the Fourier transform of the image. Large filters are more efficient applied in the Fourier domain. 25/10/2021 Computer Vision I: Fourier Transform 39

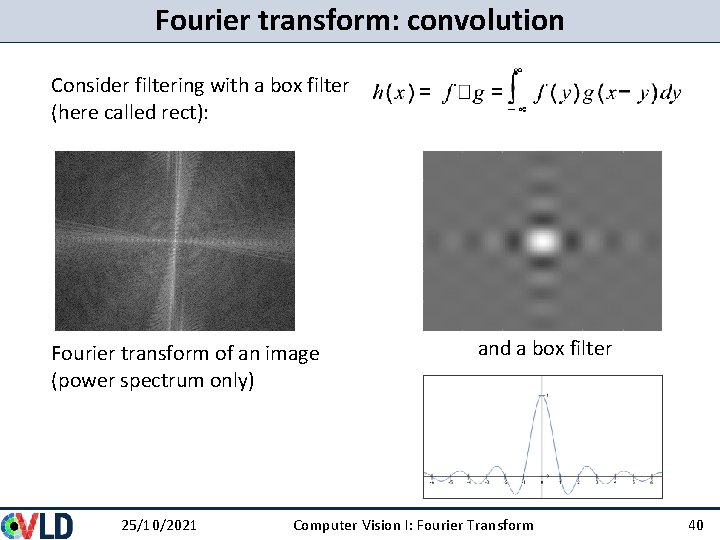
Fourier transform: convolution Consider filtering with a box filter (here called rect): Fourier transform of an image (power spectrum only) 25/10/2021 and a box filter Computer Vision I: Fourier Transform 40

Fourier transform: correlation If we do not apply the mirroring in convolution, we get Correlation: 25/10/2021 Computer Vision I: Fourier Transform 41

Correlation With discrete input: Making this independent of offset and scaling factors we get the normalized cross correlation (NCC): 25/10/2021 Computer Vision I: Fourier Transform 42

matched Filter If a signal is corrupted with white noise, we want a suitable filter h, that maximizes the signal to noise ratio (Parceval's equality) then , by Schwarz’s inequality 25/10/2021 Computer Vision I: Fourier Transform 43

Autocorrelation Correlation of a function with itself is called Autocorrelation The Fourier transform is the power spectrum 25/10/2021 Computer Vision I: Fourier Transform 44

image restoration inverse filter Wiener filter 25/10/2021 Computer Vision I: Fourier Transform 45

Regularization Suppose we want to find a mapping function f from an input vector x to an output vector y. This problem is said to be „well posed“ if 1. a solution exists: for every input vector x there is an output vector y, 2. the solution is unique: if f(x)=f(z) then x=z, and 3. the mapping is continuous: small changes in x lead to small changes in f(x)=y. If one of these conditions is not satisfied the problem is “ill-posed”. Many problems in computer vision are ill-posed. One main reason is that cameras capture only a 2 D projection of the 3 D space. Another is that we want to have a generalization of input data that are sparse. 25/10/2021 Computer Vision I: Fourier Transform 46

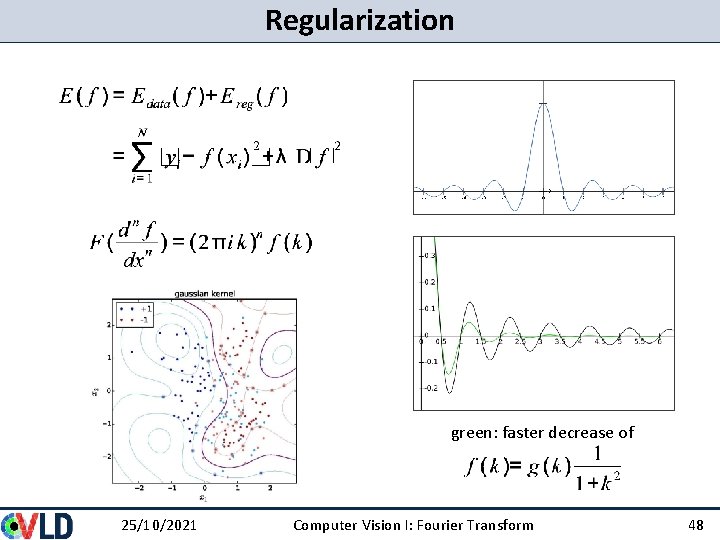
Regularization Consider a data fitting Problem were an Energy has to be optimized with respect to a fitting function f: D is a differential operator, like e. g. the Laplace, penalizing curvature. This can be viewed in the Fourier domain as penalization of high frequencies: differentiation rule 25/10/2021 Computer Vision I: Fourier Transform 47

Regularization green: faster decrease of 25/10/2021 Computer Vision I: Fourier Transform 48

uncertainty principle We consider a normalised (real) function f f and F shall have mean 0 and decrease rapidly enough that its variance is finite: further (see e. g. [1] ) from the scaling property we have uncertainty principle with ‘=’ if f is a Gaussian: 25/10/2021 Computer Vision I: Fourier Transform 49