Computer Vision Group Prof Daniel Cremers Autonomous Navigation

Geometric Primitives in 2 D § 2 D point § Augmented vector § Homogeneous

Homogeneous Vectors § Homogeneous vectors that differ only by scale represent the same 2

Geometric Primitives in 2 D § 2 D line equation Daniel Cremers Autonomous Navigation

Geometric Primitives in 2 D § Normalized line equation where and is the distance

Geometric Primitives in 2 D § Line joining two points § Intersection point of

2 D Transformations § Translation where is the translation vector, is the identity matrix,

2 D Transformations § Rigid body motion or Euclidean transf. (rotation + translation) or

2 D Transformations § Scaled rotation/similarity transform or § Preserves angles between lines Daniel

2 D Transformations § Affine transform § Parallel lines remain parallel Daniel Cremers Autonomous

2 D Transformations § Homography or projective transf. § Note that is homogeneous (only

Lessons Learned § 2 D points and 2 D lines § Homogeneous coordinates §

Slides: 12

Download presentation

Computer Vision Group Prof. Daniel Cremers Autonomous Navigation for Flying Robots Lecture 2. 2: 2 D Geometry Daniel Cremers Technische Universität München

Geometric Primitives in 2 D § 2 D point § Augmented vector § Homogeneous coordinates Daniel Cremers Autonomous Navigation for Flying Robots 2

Homogeneous Vectors § Homogeneous vectors that differ only by scale represent the same 2 D point § Convert back to inhomogeneous coordinates by dividing through last element § Points with points Daniel Cremers are called points at infinity or ideal Autonomous Navigation for Flying Robots 3

Geometric Primitives in 2 D § 2 D line equation Daniel Cremers Autonomous Navigation for Flying Robots 4

Geometric Primitives in 2 D § Normalized line equation where and is the distance of the line to the origin Daniel Cremers Autonomous Navigation for Flying Robots 5

Geometric Primitives in 2 D § Line joining two points § Intersection point of two lines Daniel Cremers Autonomous Navigation for Flying Robots 6

2 D Transformations § Translation where is the translation vector, is the identity matrix, and is the zero vector Daniel Cremers Autonomous Navigation for Flying Robots 7

2 D Transformations § Rigid body motion or Euclidean transf. (rotation + translation) or where is orthogonal ( ) with § Distances (and angles) are preserved Daniel Cremers Autonomous Navigation for Flying Robots 8

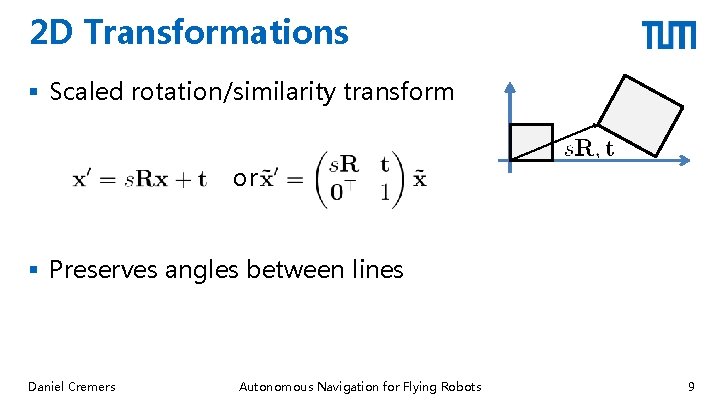
2 D Transformations § Scaled rotation/similarity transform or § Preserves angles between lines Daniel Cremers Autonomous Navigation for Flying Robots 9

2 D Transformations § Affine transform § Parallel lines remain parallel Daniel Cremers Autonomous Navigation for Flying Robots 10

2 D Transformations § Homography or projective transf. § Note that is homogeneous (only defined up to scale) § Resulting coordinates are homogeneous § Straight lines remain straight Daniel Cremers Autonomous Navigation for Flying Robots 11

Lessons Learned § 2 D points and 2 D lines § Homogeneous coordinates § 2 D transformations § Next: Example Daniel Cremers Autonomous Navigation for Flying Robots 12