Computer vision geometric models Md Atiqur Rahman Ahad

Computer vision: geometric models Md. Atiqur Rahman Ahad Based on: Computer vision: models, learning and inference. © 2011 Simon J. D. Prince

• To understand the structure of the environment from the captures images • Need to maintain accurate and realistic models of – – Lighting – Surface properties – Camera geometry – Camera and object motion 2

2. 1 Models of surface reflectance • Interaction of light with materials is key to imaging n to develop models for surfaces • Light incident on a surface is – Absorbed, – Reflected, – Scattered, and/or – Refracted 3

BRDF • For an opaque/non-transparent/solid surface, with no subsurface scattering, BRDF is a function to characterize • Bidirectional Reflectance Distribution Function (BRDF) • It is a 4 D fun that defines how light is reflected in opaque surface. 4

• Goal is to estimate and infer properties of the surface • Need simple models, e. g. , – Lambertian model – Phong model 5

2. 1. 1 Lambertian reflectance model • Lambertian model for surface reflectance: simple. • It describes surfaces whose reflectance is independent of the observer’s viewing direction. • E. g. , – Matte paint, – Unpolished wood, – Wool exhibit the Lamb. model to a reasonable accuracy. 6

• See Eq. 2. 1 • Albedo – the fraction of incident electromagnetic radiation that is reflected by the surface 7

2. 1. 2 Phone model / non. Lamb. • Many real-world materials have non. Lambertian reflectacne. • E. g. , mirror-like surfaces: they reflect incoming light in a specific direction about the local surface normal, at the point of incidence • Specular / mirror-like components and Lambartian components – together! 8

• See eq. 2. 1. 2 • 2 parts of Phong model – – Diffuse part: for Lambertian shading due to illuminant direction – Specular term: for Specular highlights 9

2. 2 Camera Models • Pinhole camera projection / model • Epipolar geomtery – consider 2 images or central projections of a 3 D scene. • Multi-view localization problem correspondence problem • Traingulation – to localize the objects in world coordinates. Need correspondence info across cameras & it is difficult to obtain • Planar images and homography [rotation matrix, translation matrix] • Camera calibration 10

Motivation Sparse stereo reconstruction Compute the depth at a set of sparse matching points Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 11

Pinhole camera model Real camera image is inverted Instead model impossible but more convenient virtual image Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 12

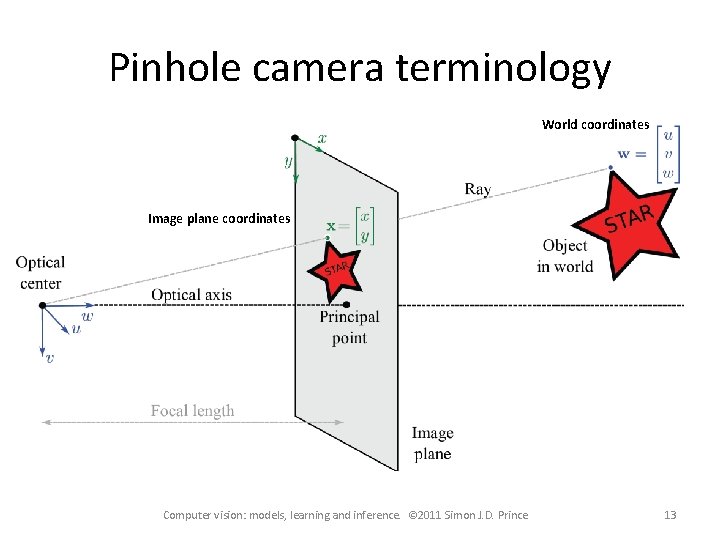
Pinhole camera terminology World coordinates Image plane coordinates Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 13

Normalized Camera By similar triangles: Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 14

Focal length parameters Can model both • the effect of the distance to the focal plane • the density of the receptors with a single focal length parameter f In practice, the receptors may not be square: So use different focal length parameter for x and y dims Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 15

Offset parameters • Current model assumes that pixel (0, 0) is where the principal ray strikes the image plane (i. e. , the center) • Model offset to center Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 16

Skew parameter • Finally, add skew parameter • Accounts for image plane being not exactly perpendicular to the principal ray Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 17

Position and orientation of camera • Position w=(u, v, w)T of point in the world is generally not expressed in the frame of reference of the camera. • Transform using 3 D transformation or Point in frame of reference of camera Point in frame of reference of world / World coordinates Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 18

Complete pinhole camera model focal length parameter f. different focal length parameter for x and y dims. Intrinsic [inherent/essential] parameters (stored as intrinsic matrix) Extrinsic [external/non-essential] parameters Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 19

Complete pinhole camera model For short: Add noise – uncertainty in localizing feature in image Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 20

Radial distortion Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 21

2. 2. 2 Epipolar geometry The principle of triangulation in stereo imaging. http: //homepages. inf. ed. ac. uk/rbf/CVonline/LOCAL_COPIES/OWENS/LECT 10/node 3. html 22

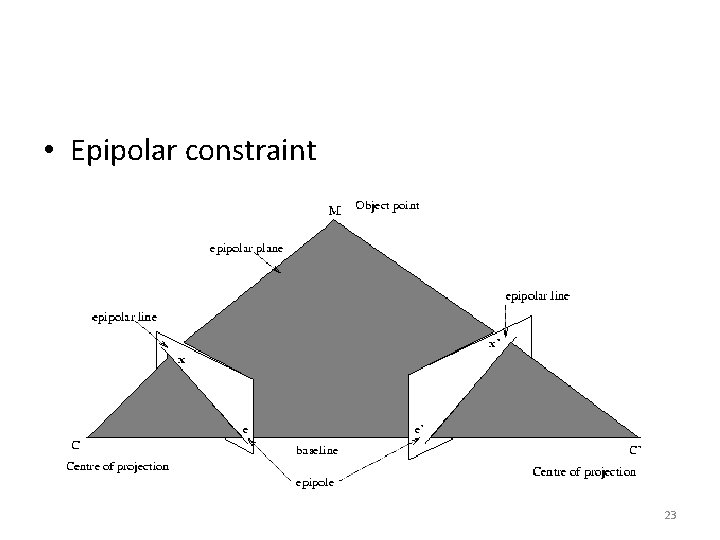
• Epipolar constraint 23

• The epipole is the point of intersection of the line joining the optical centres, that is the baseline, with the image plane. Thus the epipole is the image, in one camera, of the optical centre of the other camera. • The epipolar plane is the plane defined by a 3 D point M and the optical centres C and C'. • The epipolar line is the straight line of intersection of the epipolar plane with the image plane. It is the image in one camera of a ray through the optical centre and image point in the other camera. All epipolar lines intersect at the epipole. 24

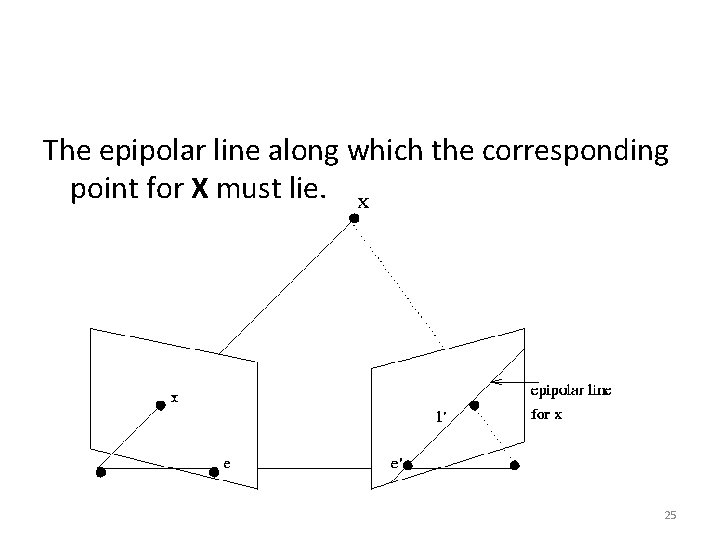
The epipolar line along which the corresponding point for X must lie. 25

Conclusion • Pinhole camera model is a non-linear function that takes points in 3 D world and finds where they map to in image • Parameterized by intrinsic and extrinsic matrices • Difficult to estimate intrinsic/extrinsic/depth because non-linear • Use homogeneous coordinates where we can get closed form solutions (initial sol’ns only) Computer vision: models, learning and inference. © 2011 Simon J. D. Prince 26