Computer Vision Geometric Camera Models and Camera Calibration

Computer Vision Geometric Camera Models and Camera Calibration Bahadir K. Gunturk

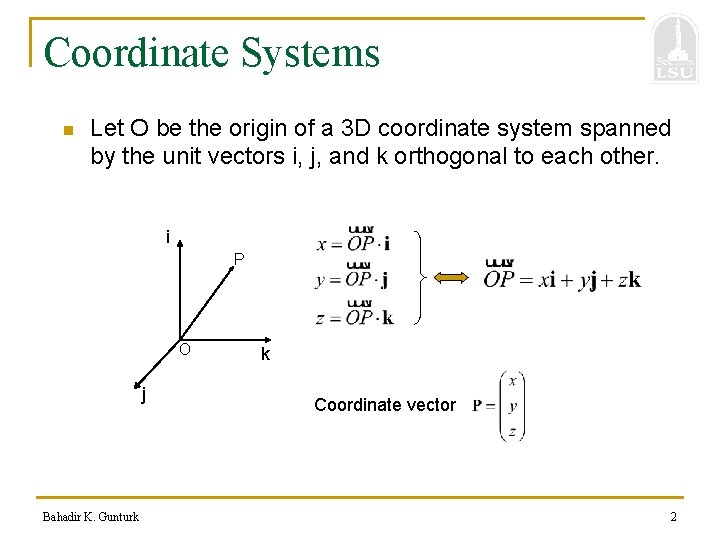
Coordinate Systems n Let O be the origin of a 3 D coordinate system spanned by the unit vectors i, j, and k orthogonal to each other. i P O j Bahadir K. Gunturk k Coordinate vector 2

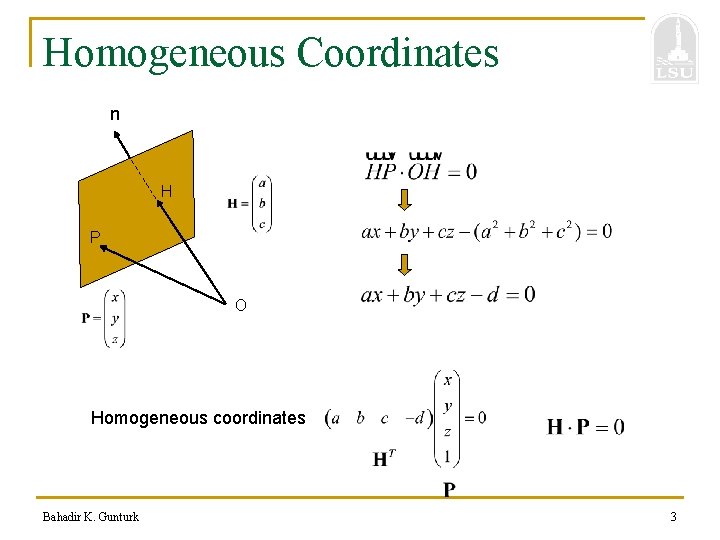
Homogeneous Coordinates n H P O Homogeneous coordinates Bahadir K. Gunturk 3

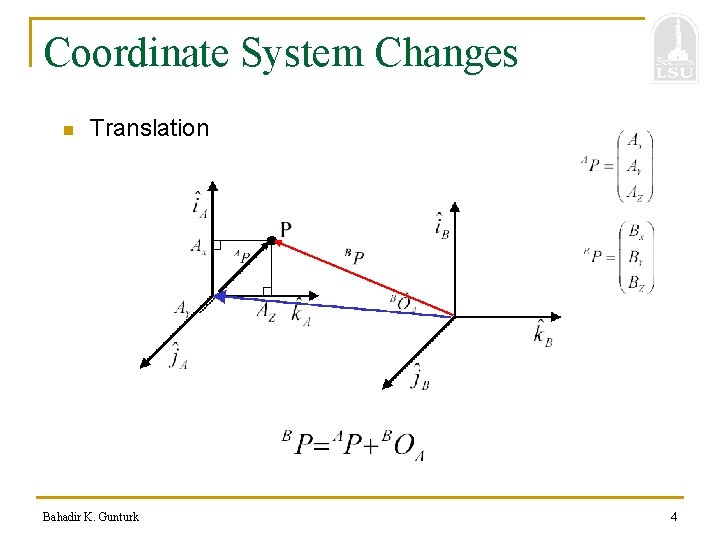
Coordinate System Changes n Translation Bahadir K. Gunturk 4

Coordinate System Changes n Rotation where Exercise: Write the rotation matrix for a 2 D coordinate system. Bahadir K. Gunturk 5

Coordinate System Changes n Rotation + Translation In homogeneous coordinates Rigid transformation matrix Bahadir K. Gunturk 6

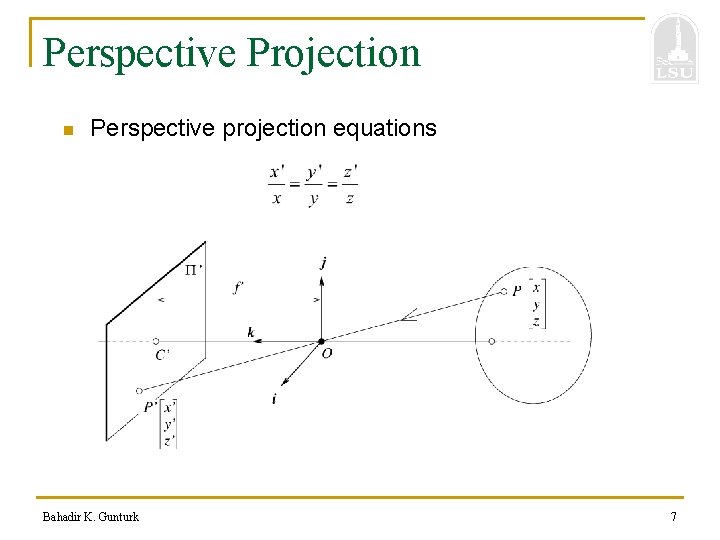
Perspective Projection n Perspective projection equations Bahadir K. Gunturk 7

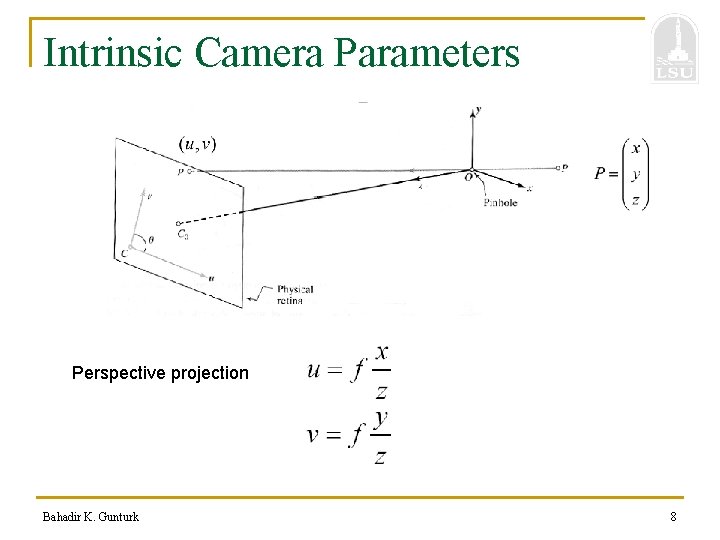
Intrinsic Camera Parameters Perspective projection Bahadir K. Gunturk 8

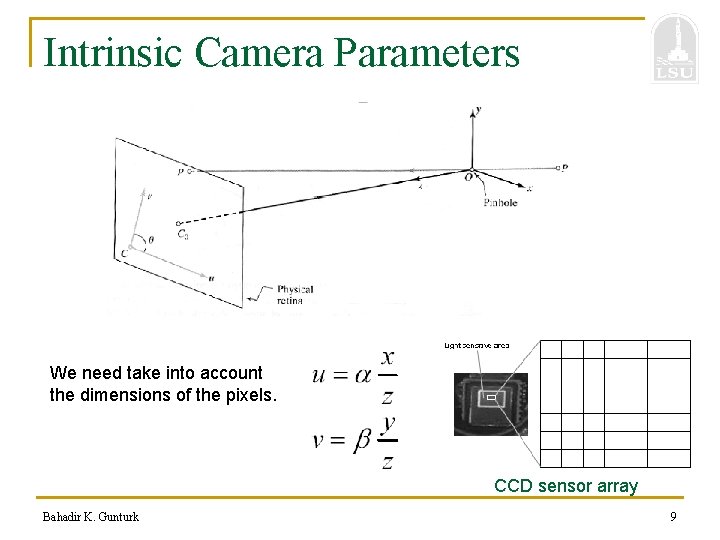
Intrinsic Camera Parameters We need take into account the dimensions of the pixels. CCD sensor array Bahadir K. Gunturk 9

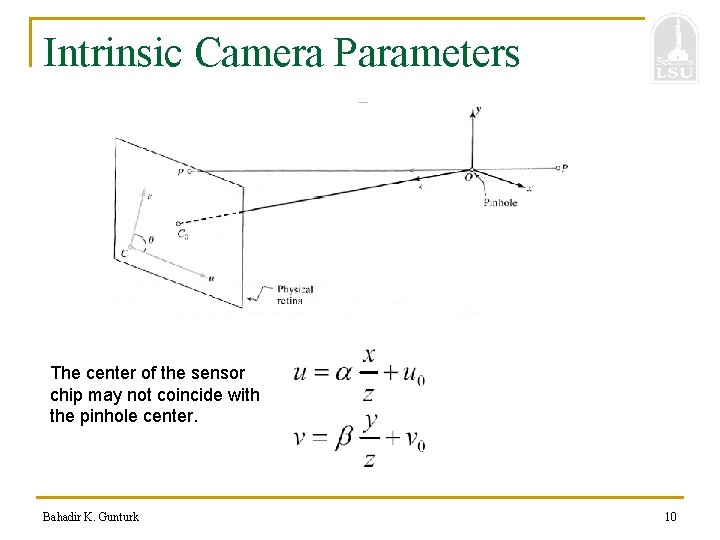
Intrinsic Camera Parameters The center of the sensor chip may not coincide with the pinhole center. Bahadir K. Gunturk 10

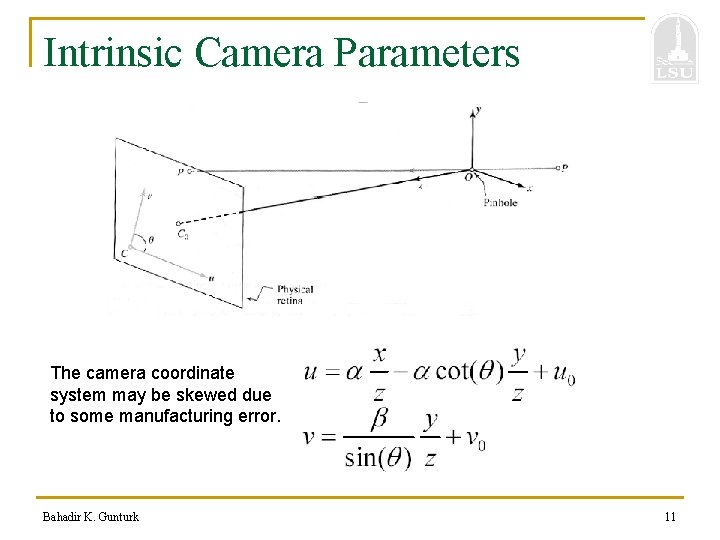
Intrinsic Camera Parameters The camera coordinate system may be skewed due to some manufacturing error. Bahadir K. Gunturk 11

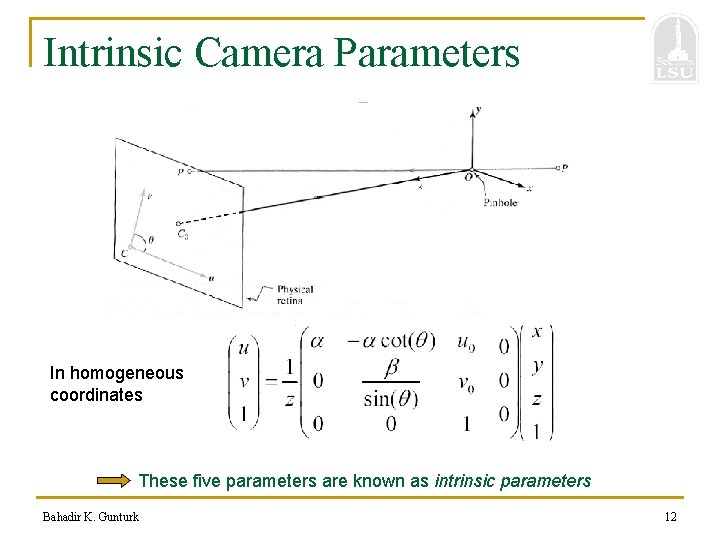
Intrinsic Camera Parameters In homogeneous coordinates These five parameters are known as intrinsic parameters Bahadir K. Gunturk 12

Intrinsic Camera Parameters In a simpler notation: With respect to the camera coordinate system Bahadir K. Gunturk 13

Extrinsic Camera Parameters n Translation and rotation of the camera frame with respect to the world frame In homogeneous coordinates Using Bahadir K. Gunturk , we get 14

Combine Intrinsic & Extrinsic Parameters We can further simplify to 3 x 4 matrix with 11 degrees of freedom: 5 intrinsic, 3 rotation, and 3 translation parameters. Bahadir K. Gunturk 15

Camera Calibration n Camera’s intrinsic and extrinsic parameters are found using a setup with known positions in some fixed world coordinate system. Bahadir K. Gunturk 16

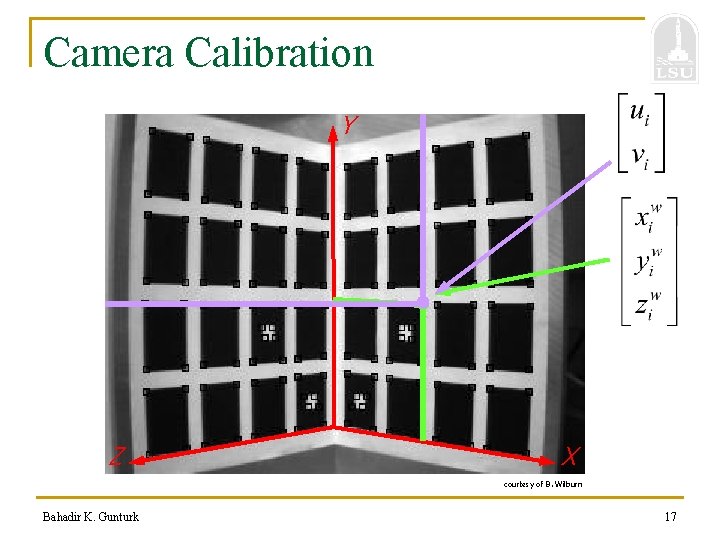
Camera Calibration Y Z X courtesy of B. Wilburn Bahadir K. Gunturk 17

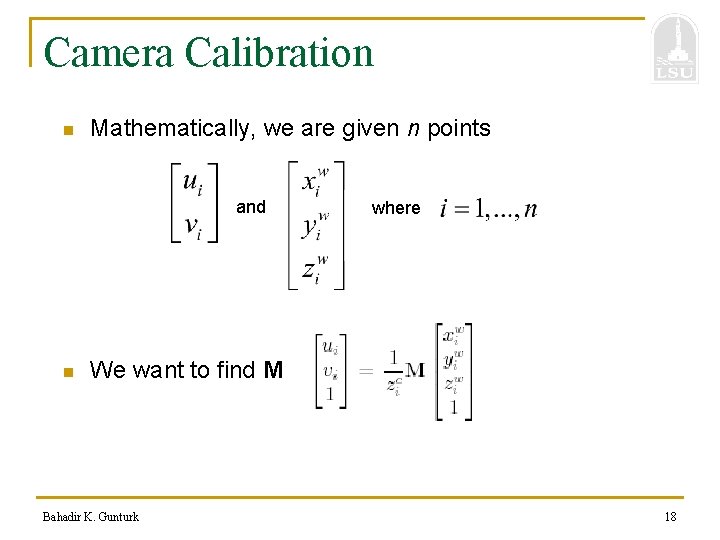
Camera Calibration n Mathematically, we are given n points and n where We want to find M Bahadir K. Gunturk 18

Camera Calibration n We can write Bahadir K. Gunturk 19

Camera Calibration n Scale and subtract last row from first and second rows to get Bahadir K. Gunturk 20

Camera Calibration n Write in matrix form for n points to get Let m 34=1; that is, scale the projection matrix by m 34. Bahadir K. Gunturk 21

Camera Calibration n The least square solution of n From the matrix M, we can find the intrinsic and extrinsic parameters. Bahadir K. Gunturk is 22

Camera Calibration n Consider the case where skew angle is 90. Since we set m 34=1, we need to take that into account at the end. Notice that Since R is a rotation matrix, Therefore, Bahadir K. Gunturk 23

Camera Calibration n We get See Forsyth & Ponce for details and skew-angle case. Bahadir K. Gunturk 24

Applications First-down line courtesy of Sportvision Bahadir K. Gunturk 25

Applications Virtual advertising courtesy of Princeton Video Image Bahadir K. Gunturk 26

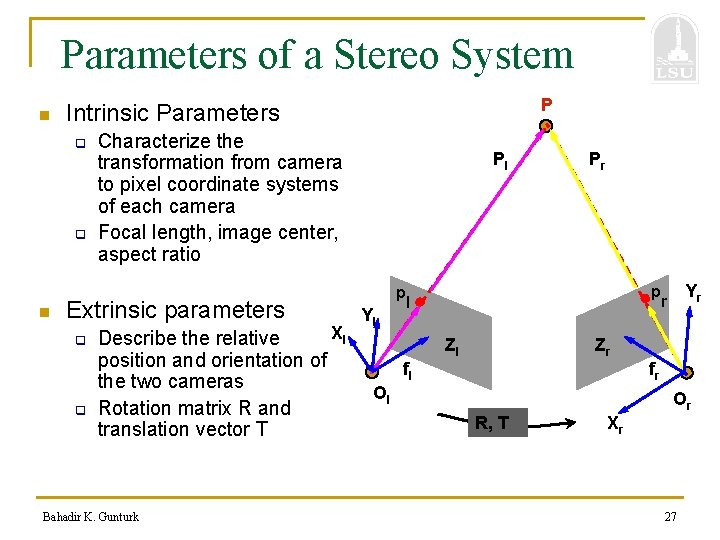
Parameters of a Stereo System n q q n P Intrinsic Parameters Characterize the transformation from camera to pixel coordinate systems of each camera Focal length, image center, aspect ratio Extrinsic parameters q q Xl Describe the relative position and orientation of the two cameras Rotation matrix R and translation vector T Bahadir K. Gunturk Pl p Yl Pr p l Zl Yr r Zr fl fr Ol Or R, T Xr 27

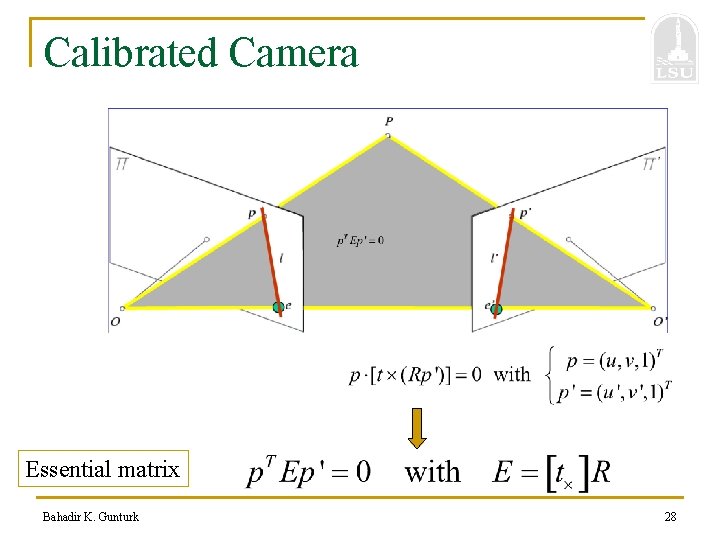
Calibrated Camera Essential matrix Bahadir K. Gunturk 28

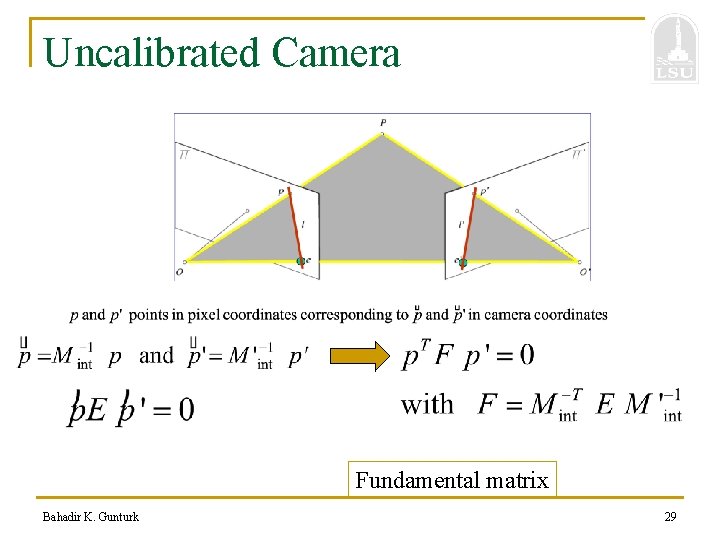
Uncalibrated Camera Fundamental matrix Bahadir K. Gunturk 29