Computer Vision cmput 428615 Lecture 8 3 D

Computer Vision cmput 428/615 Lecture 8: 3 D projective geometry and it’s applications Martin Jagersand

First 1 D Projective line Projective Coordinates • Basic projective invariant in P 1: the cross ratio a b d c ac bd = ac bd inhomogeneous Requires 4 points: 3 to create a coordinate system The fourth is positioned within that system b a d c

Cross ratio HZ CH 2. 5 • Basic projective invariant in P 1: the cross ratio homogeneous • Properties: – Defines coordinates along a 1 d projective line – Independent of the homogeneous representation of x – Valid for ideal points – Invariant under homographies

Projective 3 D space • Points • Planes Points and planes are dual in 3 d projective space. • Lines: 5 DOF, various parameterizations • Projective transformation: – 4 x 4 nonsingular matrix –Point transformation –Plane transformation H • Quadrics: Q – 4 x 4 symmetric matrix Q – 9 DOF (defined by 9 points in general pose) Dual: Q*

3 D points 3 D point in R 3 in P 3 projective transformation (4 x 4 -1=15 dof)

Planes 3 D plane Transformation Euclidean representation Dual: points ↔ planes, lines ↔ lines

Planes from points (solve as right nullspace of Or implicitly from coplanarity condition )

Representing a plane by by lin comb of 3 points Representing a plane by its nullspace span M All points lin comb of basis Canonical form: Given a plane nullspace span M is

Points from planes (solve as right nullspace of )

Lines Join of two points: A, B (4 dof) Intersection of two planes: P, Q Example: X-axis

Points, lines and planes Join of point X and line W is plane Intersection of line W with plane is point X

Affine space Difficulties with a projective space: – Nonintuitive notion of direction: A – Parallelism is not represented +/- B – Infinity not distinguished – No notion of “inbetweenness”: – Projective lines are topologically circular – Only cross-ratios are available – Ratios are required for many practical tasks Solution: find the plane at infinity! • Transform the model to give ∞ its canonical coordinates • 2 D analogy: fix the horizon line Determining the plane at infinity upgrades the geometry from projective to affine

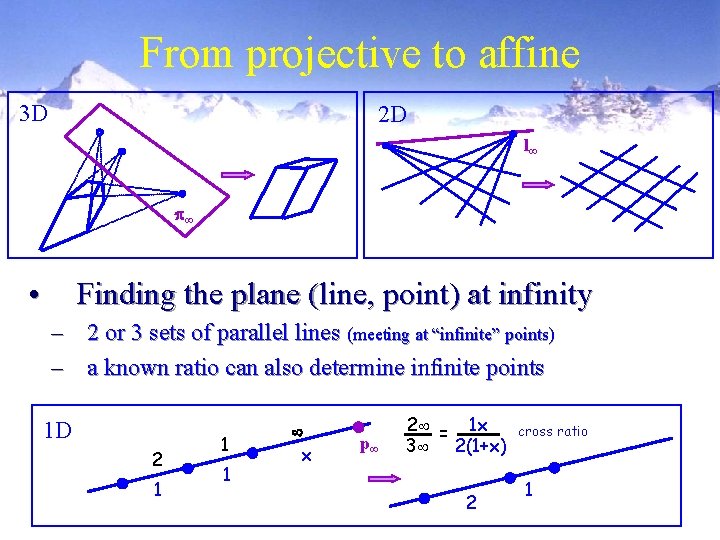
From projective to affine 3 D 2 D l • Finding the plane (line, point) at infinity – 2 or 3 sets of parallel lines (meeting at “infinite” points) – a known ratio can also determine infinite points 1 D 2 1 1 1 x p 2 = 1 x 3 2(1+x) 2 cross ratio 1

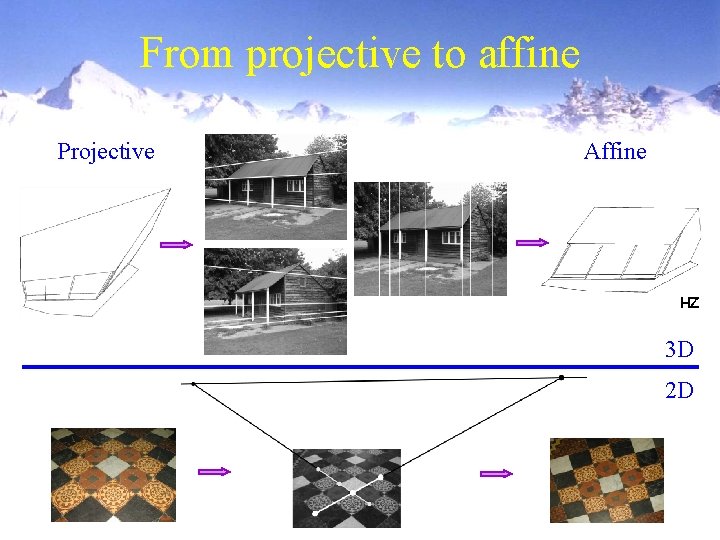
From projective to affine Projective Affine HZ 3 D 2 D

Affine space • Affine transformation – 12 DOF – Leaves unchanged • Invariants – Ratio of lengths on a line – Ratios of angles – Parallelism Kutulakos and Vallino, Calibration. Free Augmented Reality, 1998

Metric space • Metric transformation (similarity) – 7 DOF – Maps absolute conic to itself • Invariants – Length ratios – Angles – The absolute conic Without a yard stick, this is the highest level of geometric structure that can be retrieved from images

The absolute conic • Absolute conic is an imaginary circle on • It is the intersection of every sphere with • In a metric frame On : absolute dual quadric

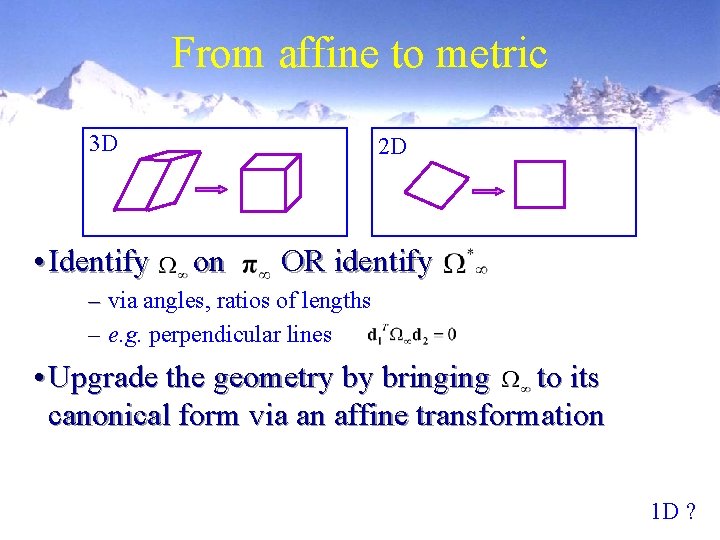
From affine to metric 3 D • Identify 2 D on OR identify – via angles, ratios of lengths – e. g. perpendicular lines • Upgrade the geometry by bringing to its canonical form via an affine transformation 1 D ?

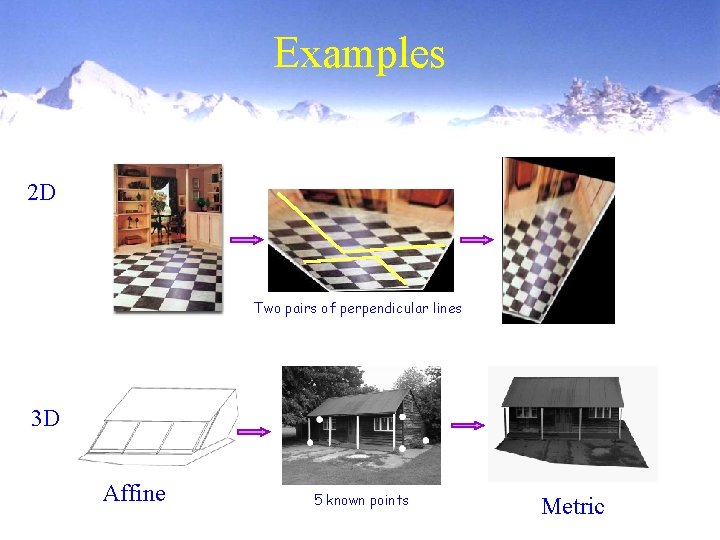
Examples 2 D Two pairs of perpendicular lines 3 D Affine 5 known points Metric

What good is a projective model? Represents fundamental feature interactions Used in rendering with an unconventional engine: Physical Objects! Tcol(f 1, f 2, f 3) = f 1 - f 2 f 3 Visual Servoing Achieving 3 d tasks via 2 d image control f 3 f 1 collinearity task f 2

What good is a projective model? Represents fundamental feature interactions Used in rendering with an unconventional engine: Physical Objects! Visual Servoing Achieving 3 d tasks via 2 d image control y 11 y 23 y 13 Y 21 y 12 y 22 image collinearity constraint

Collinearity? A point meets a line in each of two images. . .

Collinearity? But it doesn’t guarantee task achievement !

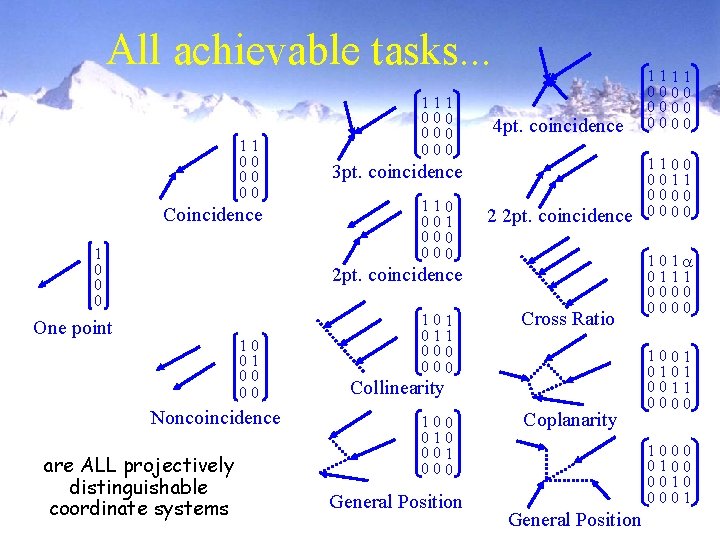
All achievable tasks. . . 11 00 00 00 Coincidence 1 0 0 0 111 000 000 4 pt. coincidence 1111 0000 2 2 pt. coincidence 1100 0011 0000 3 pt. coincidence 110 001 000 2 pt. coincidence One point 10 01 00 00 Noncoincidence are ALL projectively distinguishable coordinate systems 101 011 000 Cross Ratio 100 010 001 000 Coplanarity Collinearity General Position 1 0111 0000 1001 0101 0011 0000 1000 0100 0010 0001 General Position

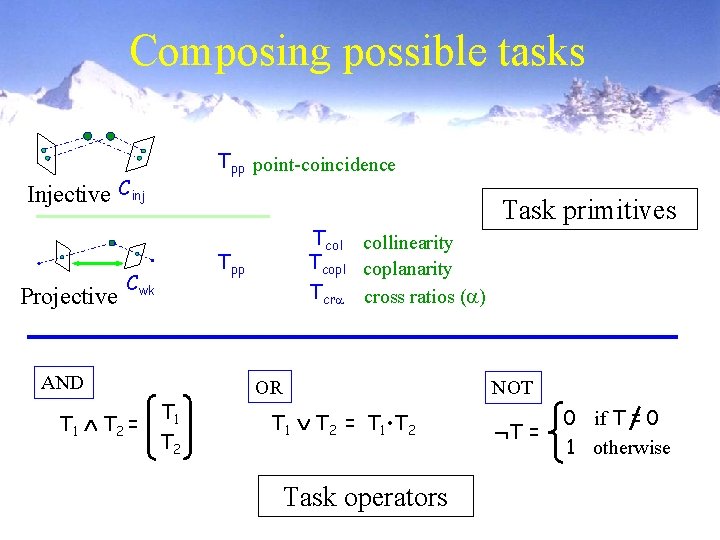
Composing possible tasks Tpp point-coincidence Injective Cinj Projective Tpp Cwk AND T 1 T 2 = Tcol collinearity Tcoplanarity Tcr cross ratios ( ) T 1 T 2 OR T 1 T 2 = T 1 • T 2 Task operators Task primitives NOT T = 0 if T = 0 1 otherwise

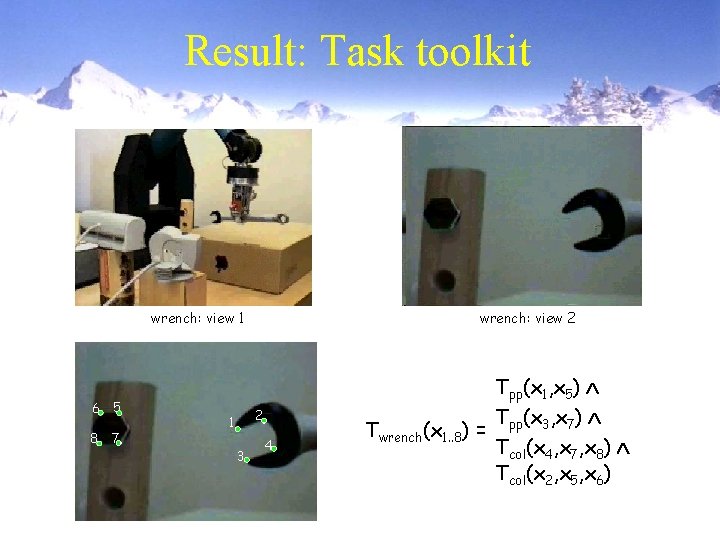
Result: Task toolkit wrench: view 1 6 5 8 7 wrench: view 2 2 1 3 4 Tpp(x 1, x 5) Tpp(x 3, x 7) Twrench(x 1. . 8) = Tcol(x 4, x 7, x 8) Tcol(x 2, x 5, x 6)

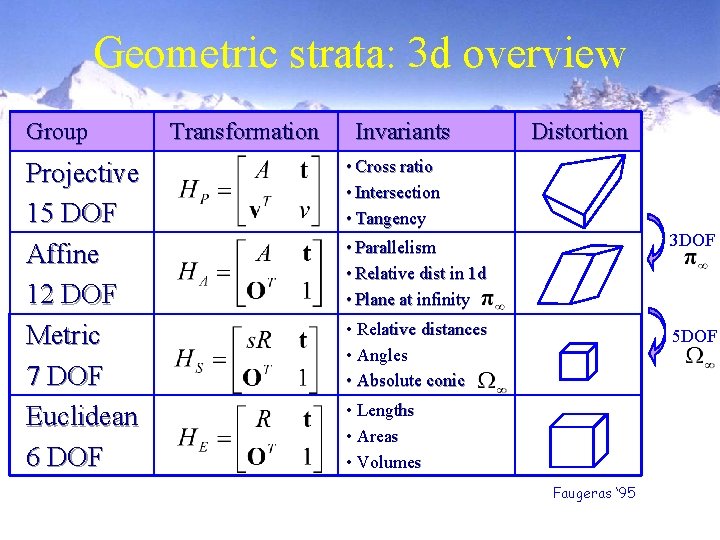
Geometric strata: 3 d overview Group Projective 15 DOF Affine 12 DOF Metric 7 DOF Euclidean 6 DOF Transformation Invariants Distortion • Cross ratio • Intersection • Tangency • Parallelism • Relative dist in 1 d • Plane at infinity 3 DOF • Relative distances • Angles • Absolute conic 5 DOF • Lengths • Areas • Volumes Faugeras ‘ 95

Perspective and projection • Euclidean geometry is not the only representation - for building models from images - for building images from models • But when 3 d realism is the goal, how can we effectively build and use projective affine metric representations ?