Computer Systems Optimizing program performance University of Amsterdam

Computer Systems Optimizing program performance University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 1

Performance can make the difference • Use Pointers instead of array indices • Use doubles instead of floats • Optimize inner loops v Recommendations Patrick van der Smagt in 1991 for neural net implementations University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 2

Machine-independent versus Machine-dependent optimizations – Optimizations you should do regardless of processor / compiler • • Code Motion (out of the loop) Reducing procedure calls Unneeded Memory usage Share Common sub-expressions – Machine-Dependent Optimizations • Pointer code • Unrolling • Enabling instruction level parallelism University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 3

Machine dependent One has to known today’s architectures • Superscalar (Pentium) (often two instructions/cycle) • Dynamic execution (P 6) (three instructions out-of-order/cycle) • Explicit parallelism (Itanium) (six execution units) University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 4

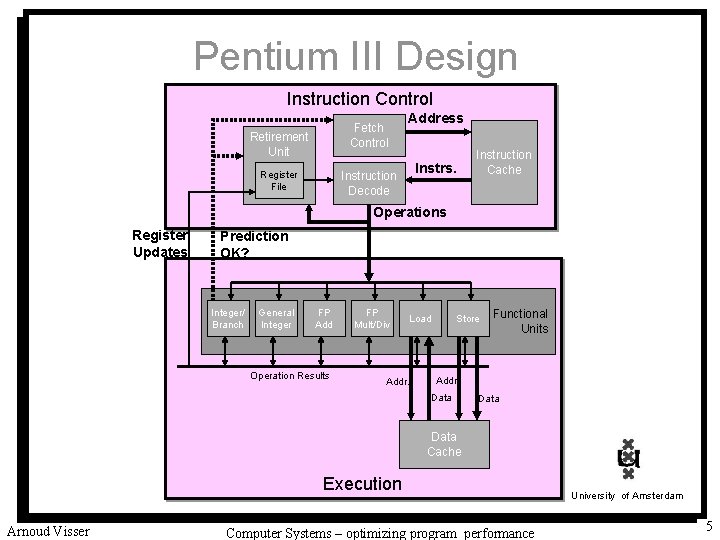
Pentium III Design Instruction Control Fetch Control Retirement Unit Register File Address Instrs. Instruction Decode Instruction Cache Operations Register Updates Prediction OK? Integer/ Branch General Integer FP Add Operation Results FP Mult/Div Load Addr. Store Functional Units Addr. Data Cache Execution Arnoud Visser Computer Systems – optimizing program performance University of Amsterdam 5

Functional Units of Pentium III • Multiple Instructions Can Execute in Parallel – 1 load – 1 store – 2 integer (one may be branch) – 1 FP Addition – 1 FP Multiplication or Division University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 6

Performance of Pentium III operations • Many instructions can be Pipelined to 1 cycle Instruction Latency – Load / Store 3 – Integer Multiply 4 – Integer Divide 36 – Double/Single FP Multiply 5 – Double/Single FP Add – Double/Single FP Divide Cycles/Issue 1 1 36 2 3 1 38 38 University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 7

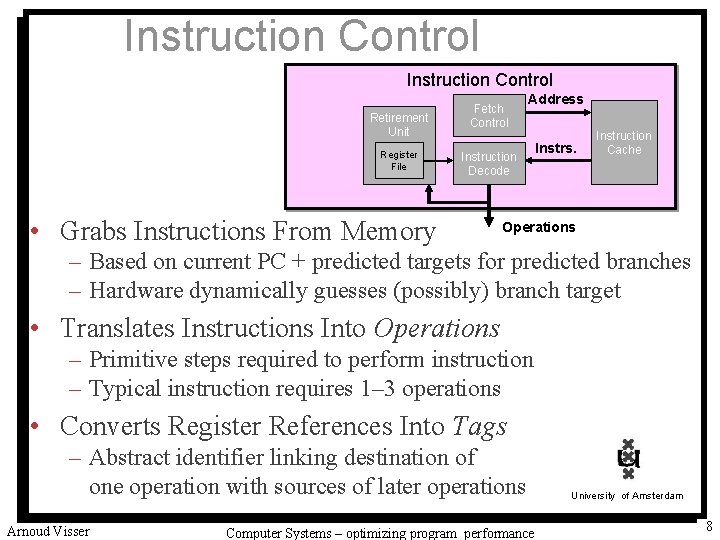
Instruction Control Retirement Unit Register File Fetch Control Address Instruction Decode • Grabs Instructions From Memory Instrs. Instruction Cache Operations – Based on current PC + predicted targets for predicted branches – Hardware dynamically guesses (possibly) branch target • Translates Instructions Into Operations – Primitive steps required to perform instruction – Typical instruction requires 1– 3 operations • Converts Register References Into Tags – Abstract identifier linking destination of one operation with sources of later operations Arnoud Visser Computer Systems – optimizing program performance University of Amsterdam 8

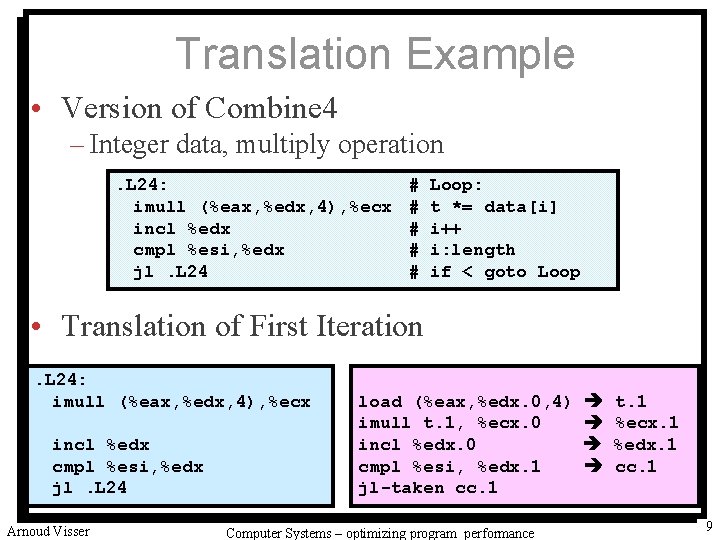
Translation Example • Version of Combine 4 – Integer data, multiply operation. L 24: imull (%eax, %edx, 4), %ecx incl %edx cmpl %esi, %edx jl. L 24 # # # Loop: t *= data[i] i++ i: length if < goto Loop • Translation of First Iteration. L 24: imull (%eax, %edx, 4), %ecx incl %edx cmpl %esi, %edx jl. L 24 Arnoud Visser load (%eax, %edx. 0, 4) t. 1 imull t. 1, %ecx. 0 %ecx. 1 incl %edx. 0 %edx. 1 cmpl %esi, %edx. 1 cc. 1 jl-taken cc. 1 University of Amsterdam Computer Systems – optimizing program performance 9

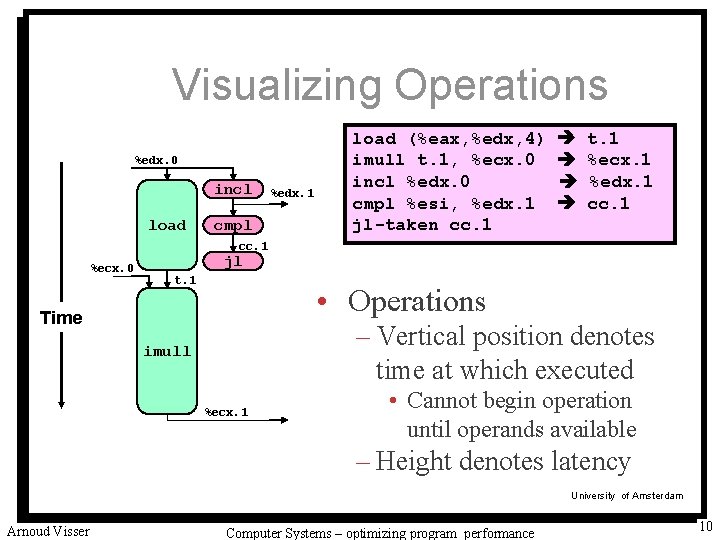
Visualizing Operations %edx. 0 incl load cmpl %edx. 1 load (%eax, %edx, 4) imull t. 1, %ecx. 0 incl %edx. 0 cmpl %esi, %edx. 1 jl-taken cc. 1 t. 1 %ecx. 1 %edx. 1 cc. 1 %ecx. 0 jl t. 1 • Operations Time – Vertical position denotes time at which executed imull %ecx. 1 • Cannot begin operation until operands available – Height denotes latency University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 10

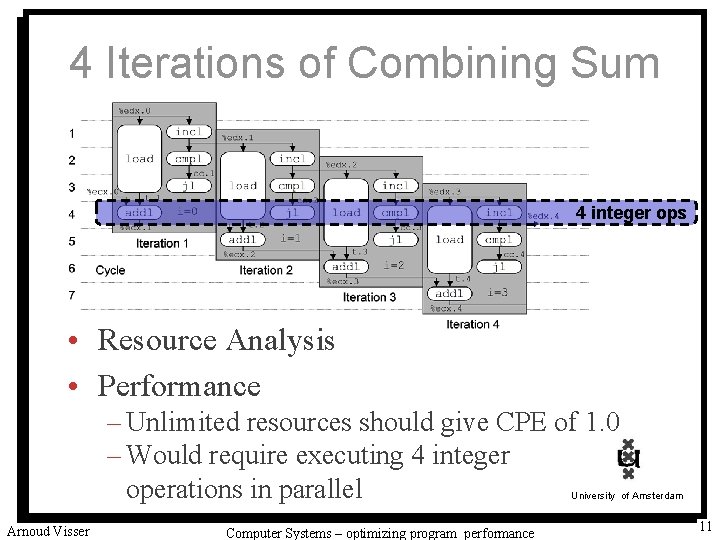
4 Iterations of Combining Sum 4 integer ops • Resource Analysis • Performance – Unlimited resources should give CPE of 1. 0 – Would require executing 4 integer operations in parallel University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 11

Pentium Resource Constraints – Only two integer functional units – Set priority based on program order Performance – Sustain CPE of 2. 0 Arnoud Visser Computer Systems – optimizing program performance University of Amsterdam 12

Loop Unrolling • Optimization – Combine multiple iterations into single loop body – Amortizes loop overhead across multiple iterations – Finish extras at end Arnoud Visser – Measured CPE=1. 33 void combine 5(vec_ptr v, int *dest) { int length = vec_length(v); int limit = length-2; int *data = get_vec_start(v); int sum = 0; int i; /* Combine 3 elements at a time */ for (i = 0; i < limit; i+=3) { sum += data[i] + data[i+2] + data[i+1]; } /* Finish any remaining elements */ for (; i < length; i++) { sum += data[i]; } *dest = sum; } University of Amsterdam Computer Systems – optimizing program performance 13

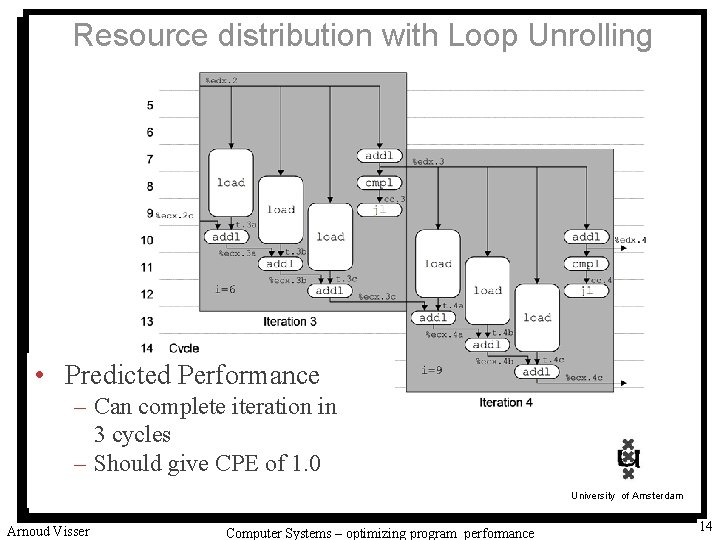
Resource distribution with Loop Unrolling • Predicted Performance – Can complete iteration in 3 cycles – Should give CPE of 1. 0 University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 14

Effect of Unrolling Degree Intege Sum r 1 2 2. 00 1. 50 3 4 8 16 1. 33 1. 50 1. 25 1. 06 Intege Product 4. 00 r • Only examples FP Sumhelps integer sum for our 3. 00 cases constrained by functional FP – Other Product 5. 00 unit latencies • Effect is nonlinear with degree of unrolling • Many subtle effects determine exact scheduling of operations University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 15

Unrolling is for long vectors Unrolling Degree 1 2 Int. Sum ∞ 2. 00 1. 50 Int. Sum 1024 2. 06 1. 56 Int. Sum 31 4. 02 3. 57 3 1. 33 1. 40 3. 39 4 1. 50 1. 56 3. 84 8 1. 25 1. 31 3. 91 16 1. 06 1. 12 3. 66 • New source of overhead – The need to finish the remaining elements when the vector length is not divisible by the degree of unrolling University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 16

3 Iterations of Combining Product • Unlimited Resource Analysis – Assume operation can start as soon as operands available • Performance – Limiting factor becomes latency – Gives CPE of 4. 0 University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 17

Iteration splitting void combine 6(vec_ptr v, int *dest) { int length = vec_length(v); int limit = length-1; int *data = get_vec_start(v); int x 0 = 1; int x 1 = 1; int i; /* Combine 2 elements at a time */ for (i = 0; i < limit; i+=2) { x 0 *= data[i]; x 1 *= data[i+1]; } /* Finish any remaining elements */ for (; i < length; i++) { x 0 *= data[i]; } *dest = x 0 * x 1; } Arnoud Visser • Optimization – Make operands available by accumulating in two different products (x 0, x 1) – Combine at end • Performance – CPE = 2. 0 Computer Systems – optimizing program performance University of Amsterdam 18

Resource distribution with Iteration Splitting – Predicted Performance • Make use of both execution units • Gives CPE of 2. 0 Arnoud Visser Computer Systems – optimizing program performance University of Amsterdam 19

Results for Pentium III – Biggest gain doing basic optimizations – But, last little bit helps Arnoud Visser Computer Systems – optimizing program performance University of Amsterdam 20

Results for Pentium 4 – Higher latencies (int * = 14, fp + = 5. 0, fp * = 7. 0) • Clock runs at 2. 0 GHz • Not an improvement over 1. 0 GHz P 3 for integer * – Avoids FP multiplication anomaly University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 21

Machine-Dependent Opt. Summary • Loop Unrolling – Some compilers do this automatically – Generally not as clever as what can achieve by hand • Exposing Instruction-Level Parallelism – Very machine dependent • Warning: – Benefits depend heavily on particular machine – Do only for performance-critical parts of code – Best if performed by compiler • But GCC on IA 32/Linux is not very good University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 22

Conclusion How should I write my programs, given that I have a good, optimizing compiler? • Don’t: Smash Code into Oblivion – Hard to read, maintain, & assure correctness • Do: – Select best algorithm & data representation – Write code that’s readable & maintainable • Procedures, recursion, without built-in constant limits • Even though these factors can slow down code • Focus on Inner Loops – Detailed optimization means detailed measurement University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 23

Assignment • Practice Problems – Practice Problem 5. 8: ‘Associations of aprod. ' • Optimization Lab University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 24

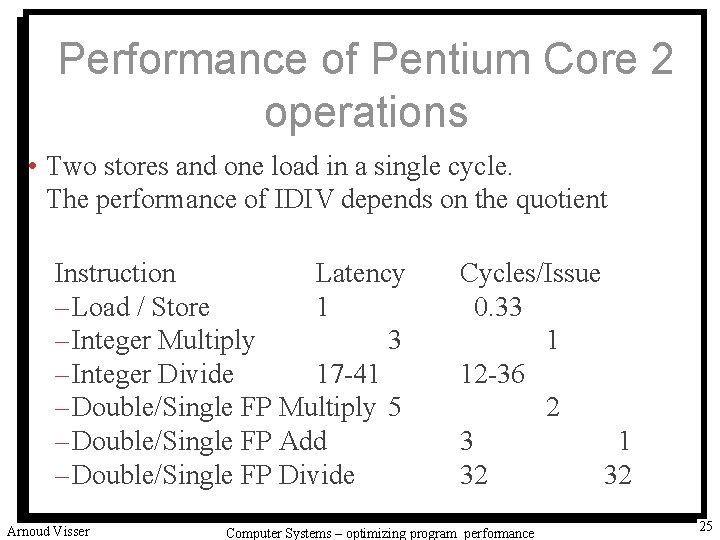
Performance of Pentium Core 2 operations • Two stores and one load in a single cycle. The performance of IDIV depends on the quotient Instruction Latency – Load / Store 1 – Integer Multiply 3 – Integer Divide 17 -41 – Double/Single FP Multiply 5 – Double/Single FP Add – Double/Single FP Divide Cycles/Issue 0. 33 1 12 -36 2 3 1 32 32 University of Amsterdam Arnoud Visser Computer Systems – optimizing program performance 25